液冷板散热流道的拓扑优化体积分数研究

刘云飞，熊 敏，丁晓红

(上海理工大学机械工程学院，上海 200093)

lyfwinder@163.com;xiongmin@usst.edu.cn;dingxh@usst.edu.cn

1 引言(Introduction)

随着高端制造业、电子芯片业及航空航天领域的发展，对各种散热技术的散热能力要求也越来越高，目前常用的散热技术主要有风冷散热(自然冷却和强迫风冷)、液冷散热和热管散热等。相较于风冷散热，液冷散热的散热效率更高；与热管等气液相变循环系统相比，单相流体的液冷循环系统也更加简易稳定。因此，液冷板散热器广泛应用于高热流密度散热系统中，其中的散热流道形态是决定液冷板性能的重要因素。传统的散热流道设计通常是基于经验的尺寸优化设计，随着近年来计算机计算能力的飞速发展，设计自由度高、灵活性强的流体拓扑优化技术已逐渐成为流体传热散热领域的主要设计手段。其方法是将散热流道设计中需要满足的各种要求和目标转化为数学模型，然后选择适当的寻优算法得到最优解。与传统的设计方法相比，拓扑优化设计方法更容易确定设计域以明确初始设计方案，且优化求解过程具有明确的数学寻优方向，其设计结果即为满足设计目标的最优设计，因而可以大大缩短设计周期。而且，随着以增材制造为代表的先进制造技术的快速发展，过去很难加工的结构，现在也可以高效地制造出来，这也让拓扑优化设计的结果能更快地转化为产品。

2 相关研究(Related works)

在散热流道拓扑优化研究中，KOGA等基于SIMP法，采用序列线性规划优化算法，将流体功率耗散和换热量加权相加作为目标函数，研究了不同权重因子：(流体功率耗散：热交换)、入口边界条件对液冷通道拓扑形态的影响，并制造了液冷板试样进行实验研究。MATSUMORI等通过对参数进行无量纲处理后重新定义积分方程，使流体进口功率恒定，并针对热载荷与结构相关、不相关两类优化问题，基于变密度法设计液冷通道形态。李昊等通过流体拓扑优化技术设计了均温板内部的散热流道，与传统流道的液冷板进行对比，并通过实验验证了优化后均温板的优秀散热性能。本文基于以流固边界换热量最大为目标的优化数学模型，对拓扑优化中的体积分数这一关键参数进行研究，设计了液冷板模型并依据数值仿真结果对体积分数的最优取值进行分析研究，并给出了由设计参数到设计结果的数学预测模型。

3 基于SIMP法的流体散热液冷板结构拓扑优化设计(Topology optimization design of liquidcooled plate based on SIMP method)

3.1 流体拓扑优化问题

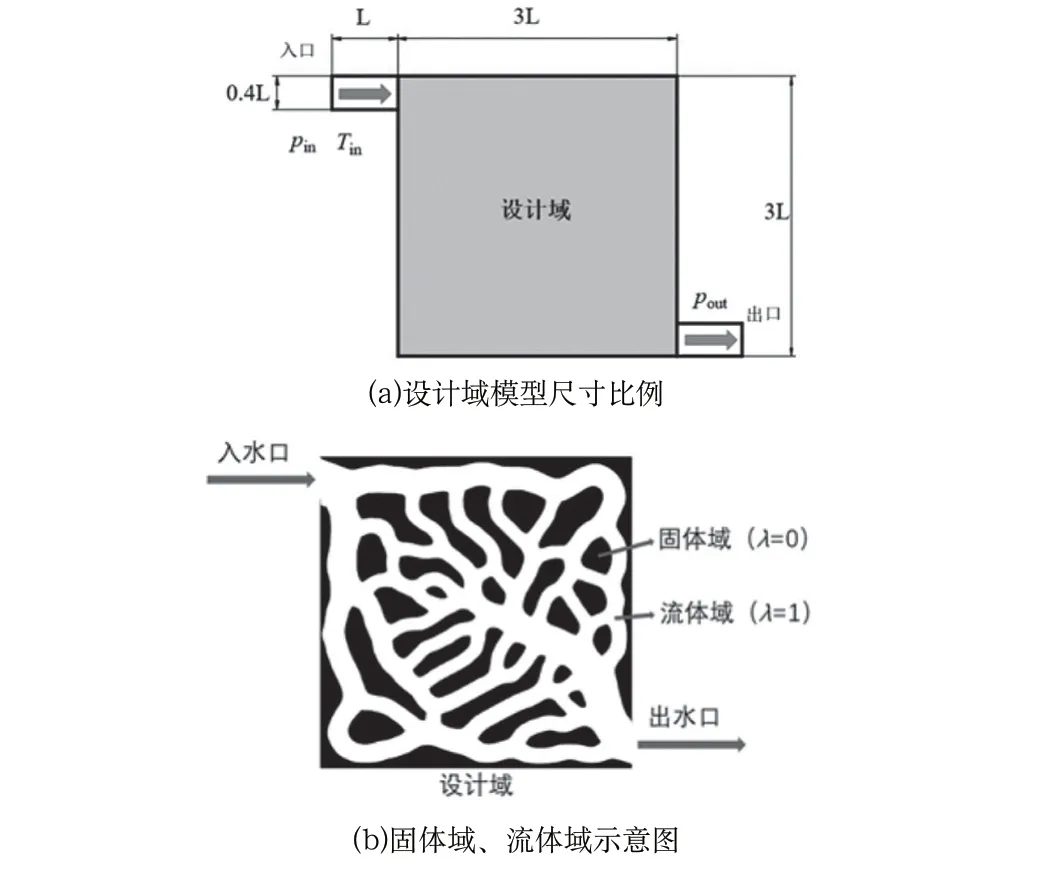
图1 流体拓扑优化模型示意图Fig.1 Schematic diagram of fluid topology optimization model

3.2 流体散热问题

根据LI等对流体拓扑优化中的共轭传热研究，针对不可压缩层流流动，需要满足连续性方程与动量守恒方程。连续性方程与动量守恒方程的无量纲形式分别通过无量纲速度 u、雷诺数、无量纲压强、无量纲梯度算子 ∇进行定义：

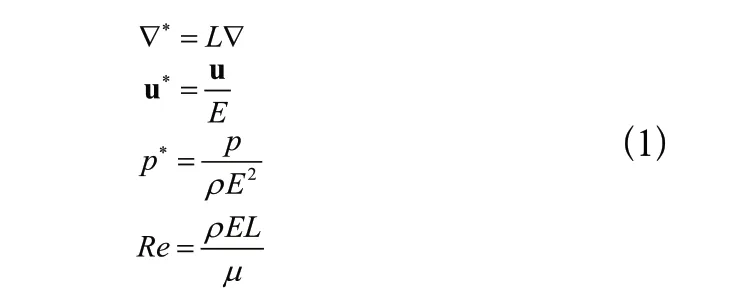
其中，为特征速度，为特征长度，为密度，为动力黏度。

根据达西定律有= -，代入动量守恒方程的体积力及流体域和固体域中能量守恒方程，可分别得到拓扑优化中流场迭代计算方程和温度场迭代计算方程，如式(2)和式(3)所示[10]：

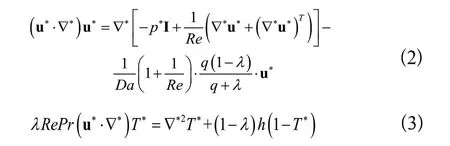
式中，为惩罚因数，本文取0.0 1；为达西数，取0.0001；流体工质为常温下的液态水，故普朗特数取6.78；流体通道最终拓扑形态与和换热系数的取值相关，本文以=100，取为300进行拓扑优化设计。由于系统内的热量最终由流过模型内部的流体带走，因此以流固边界换热量最大为目标的优化数学模型为：

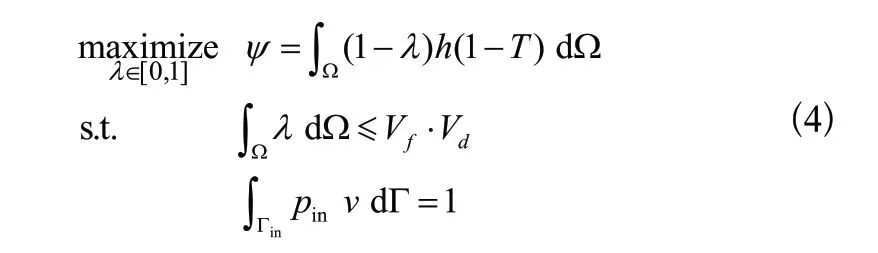
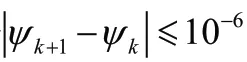
3.3 液冷板拓扑优化设计及散热性能分析

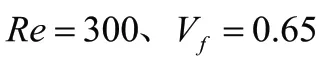
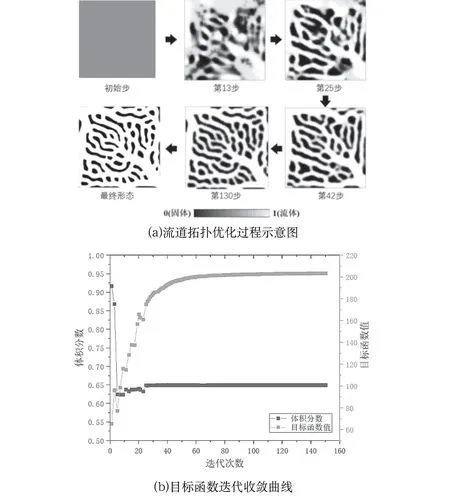
图2 流道拓扑优化过程及目标函数迭代收敛曲线Fig.2 Process of passage topology optimization and iterative convergence curve of the objective function

将得到的流道边界使用霍尔姆兹偏微分方程形式的密度过滤，再进行双曲正切投影过滤，得到清晰的流道边界。而后进行拉伸建模得到液冷板几何模型，液冷板结构尺寸如图3所示(单位：mm)。

图3 液冷板结构尺寸示意图Fig.3 Schematic diagram of structural dimensions of liquid-cooled plate

为评估拓扑流道液冷板的散热性能，在COMSOL软件平台上进行有限元仿真，采用自由四面体网格进行划分。在仿真时做出假设：(1)内部流体为不可压缩层流；(2)流固交界面无滑移边界。数值模拟时满足如下控制方程：

其中，式(5)、式(6)分别为连续性方程和动量守恒方程，式(7)为流体域的能量守恒方程，式(8)为固体域的能量守恒方程。

仿真时，冷却套的固体材料为6061铝合金，取常温20 ℃下的纯水为冷却介质；各冷却套的入口为左上侧，出口为右下侧；在入水口处施加恒定的质量流量；在冷却套内表面施加180 W恒定功率的生热源；分别取入水口雷诺数为200—1，200进行分析，其中入水口雷诺数由式(9)定义：

式中，流体密度=1.0×10kg·m； v为入口的流体速度，单位为m/s；为入口的水力直径，单位为m；流体黏度=1.008×10Pa·s。

4 流体拓扑优化中的体积分数研究 (Research on volume fraction in fluid topology optimization)

4.1 体积分数对液冷板散热性能的影响分析

在液冷板设计中，如图4(a)、图4(b)所示，在拓扑优化时增大流体域体积分数，流道平均横截面间距变宽，分支增多。流道的热交换面积与散热性能正相关，流固换热总面积为传热流道的上下壁面积(图4(c)灰色)与侧壁面积(图4(c)白色)之和。

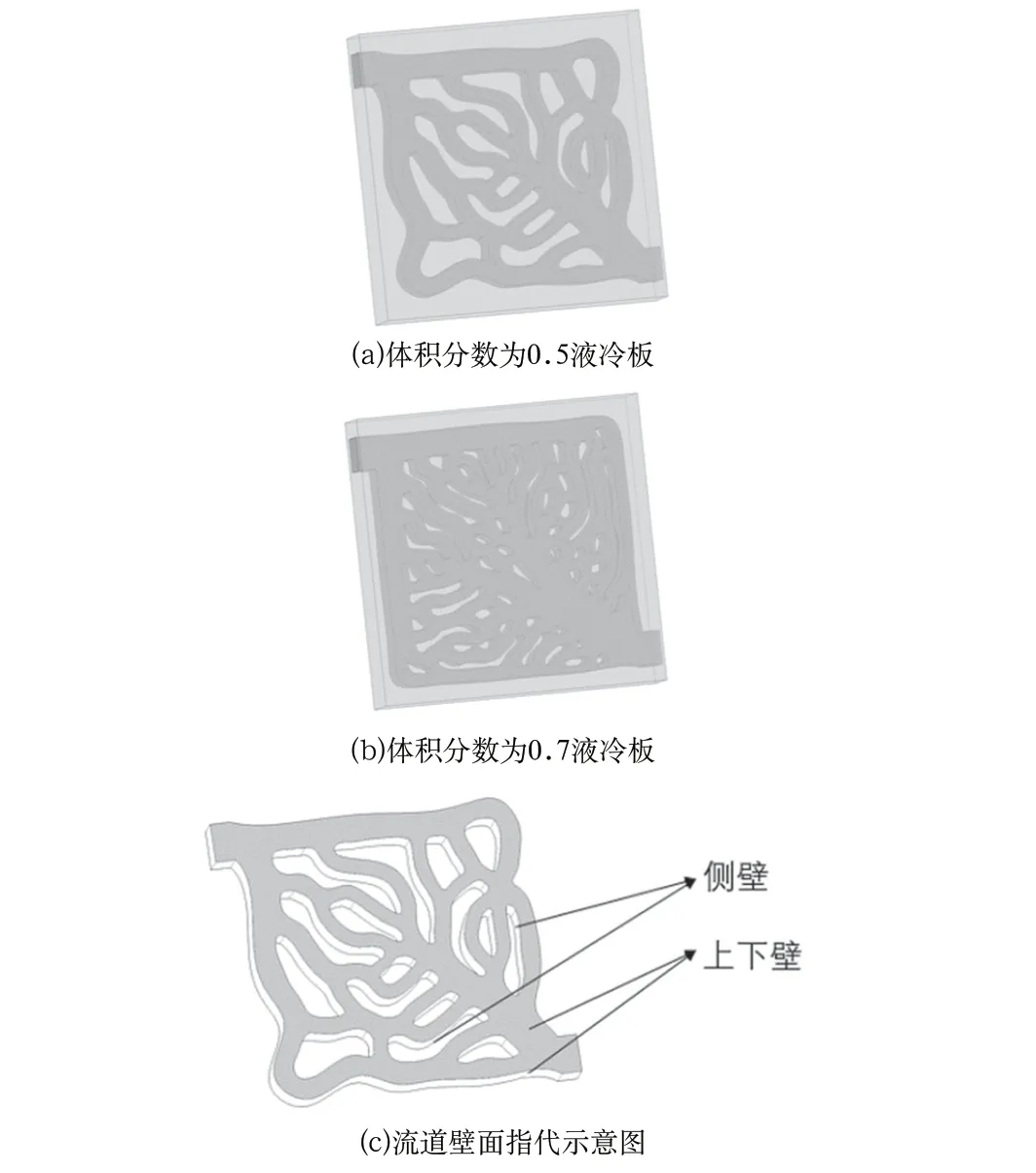
图4 不同体积分数的拓扑流道形态示意图Fig.4 Schematic diagram of topology passage patterns with different volume fraction

基于3.3.1的液冷板几何模型，流固换热总面积计算公式如下：

其中， L为拓扑优化得到的二维流道总边界长度。当流体域体积分数增大到一定程度后，固体域也随之变小，流道的总侧壁面积变小，流固换热总面积减小，液冷板的整体散热能力也随之变弱。所以，存在一个体积分数极值使拓扑优化得到的液冷板流固换热总面积最大，液冷板的散热性能最优。

为了找到该设计模型散热性能最佳的流体域体积占比，首先以0.05为步长，取体积分数分别为0.5、0.55、0.6、0.65、0.7进行拓扑优化设计，优化数学模型为式(4)。以优化得到的结果为流道进行三维建模得到五个液冷板模型，使用3.3.2中的边界条件进行仿真分析。

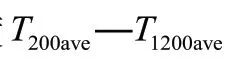
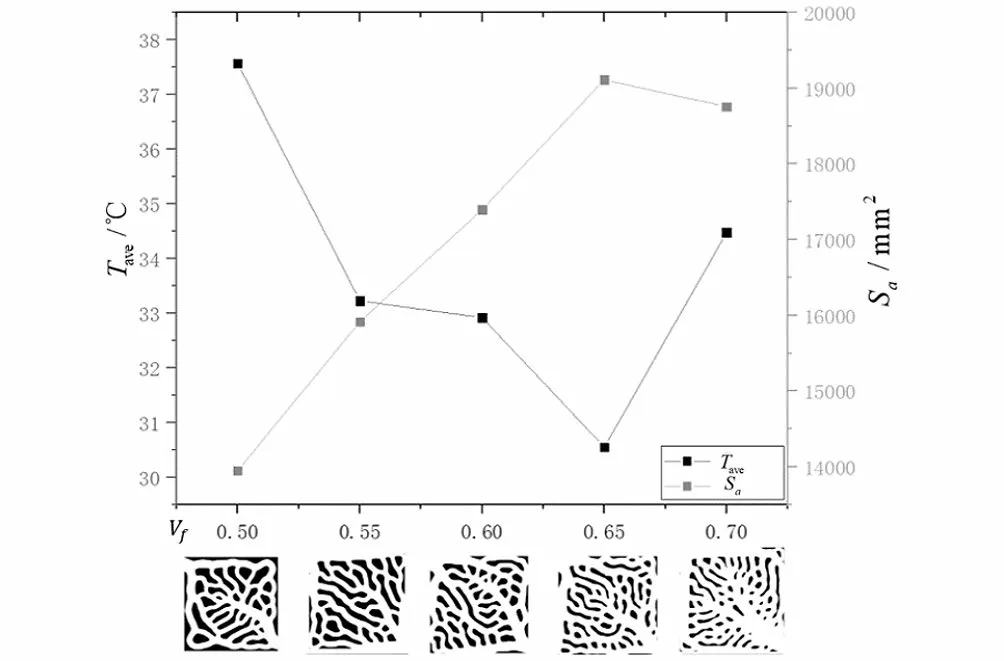
图5 V f为[0.5,0.7]的液冷板流道形态及 Tave& S a折线图Fig.5 Passage patterns of liquid-cooled plate if Vf is between 0.5 and 0.7，and their Tave& Sa line graph

基于上述分析，再以0.01为步长，取体积分数分别为0.61、0.62、0.63、0.64、0.66、0.67、0.68、0.69进行拓扑优化设计，优化数学模型为式(4)。以优化得到的结果为流道进行三维建模得到八个液冷板模型，使用3.3.2中的边界条件进行仿真分析。加上=0.65和=0.7的两个模型，对10个模型的仿真结果进行分析，绘制&折线图，如图6所示。由图6可知，在为[0.61，0.7]区间，随着的增大，流固换热总面积先单调递增再单调递减，液冷板的受热面平均温度先单调递减再单调递增，在体积分数为0.65处的最大且最低，故体积分数最优值应在(0.64，0.66)区间，在拓扑优化时建议取=0.65。

图6 V f为[0.61,0.7]的液冷板流道形态及 Tave& S a折线图Fig.6 Passage patterns of liquid-cooled plate if Vf is between 0.61 and 0.7，and their Tave& Sa line graph

4.2 在不同设计域尺寸下体积分数对拓扑优化设计结果的影响

由于热源工况形状各异，在实际生产应用时可能需要针对不同尺寸的设计域进行拓扑优化设计。为检验流体域体积分数对不同尺寸设计域的拓扑优化设计结果影响情况是否一致，在3.1所述的设计域尺寸基础上改变设计域尺寸，保持进出水口尺寸不变，将设计域边长尺寸分别设置为横∶纵=3L∶6L(图7(a))、横∶纵=6L∶3L(图7(b))。再分别以0.05为步长，取体积分数分别为0.5、0.55、0.6、0.65、0.7进行拓扑优化设计，优化数学模型为式(4)。以优化得到的结果为流道进行三维建模得到五个液冷板模型，使用3.3.2中的边界条件进行仿真分析。绘制&折线图，如图7所示，在 V为[0.5，0.7]区间，随着的增大，流固换热总面积先单调递增再单调递减，液冷板的受热面平均温度先单调递减再单调递增，在体积分数为0.65处的S最大且最低，故体积分数最优值应在0.65相邻区间。

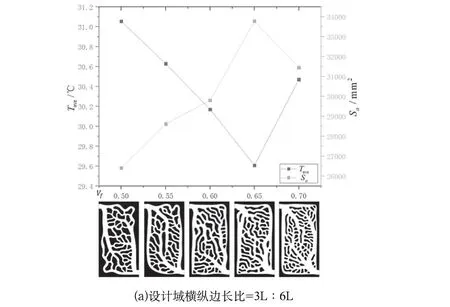
图7 V f为[0.5,0.7]的长方形设计域液冷板流道形态及 Tave& Sa折线图Fig.7 Passage patterns of liquid-cooled plate in rectangular design area if Vf is between 0.5 and 0.7，and their Tave& Sa line graph

4.3 非线性回归分析

非线性回归是回归函数关于未知回归系数具有非线性结构的回归分析方法。将4.1中仿真得到的受热面平均温度均值通过IBM SPSS进行一元非线性回归分析，得到关于的预测模型：

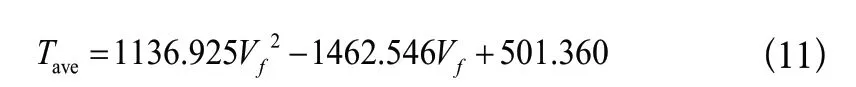
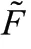
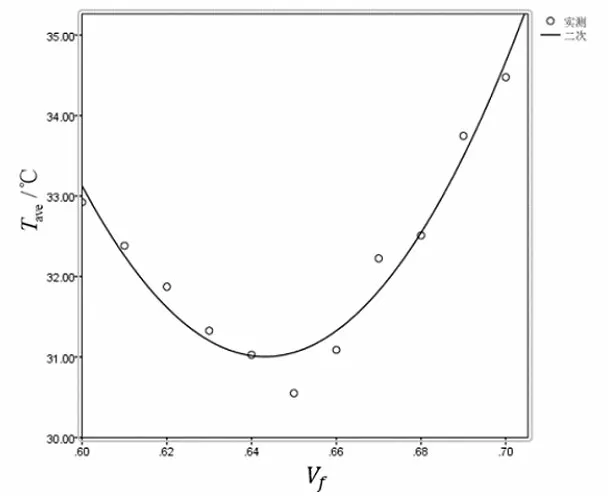
图8 非线性回归拟合曲线图Fig.8 Diagram of nonlinear regression fitting curve

5 结论(Conclusion)

本文针对基于SIMP法的流体散热液冷板拓扑优化设计中的体积分数取值问题进行了系统性的数值分析，使用控制变量法在以流固边界换热量最大为目标的优化数学模型中改变体积分数取值进行流道拓扑优化设计，并分别进行液冷板几何建模及仿真分析，统计液冷板受热面平均温度数值及流固换热总面积；而后改变设计域形状尺寸检验体积分数取值规律的普适性；最后将仿真数据进行非线性回归分析，得出体积分数对流道散热性能的预测数学模型，计算得出流体散热拓扑优化问题的体积分数最优值应在(0.64，0.65)区间的结论，为此类散热流道拓扑优化设计提供了有价值的设计指导建议。