基于改进ARMA-XGBoost 算法的汽油辛烷值损失预测模型

游长莉 唐成章 胡江宇

1.兴义民族师范学院 贵州省兴义市 562400 2.武汉纺织大学机械工程与自动化学院 湖北省武汉市 430200

1 引言

汽油是小型车辆的主要燃料，车辆保有量的增加，汽油燃料需求日益增加，燃烧其产生的尾气污染问题也日渐突显。辛烷值是反映汽油燃烧性能的重要指标，由于现有脱硫技术在对汽油进行处理时，都会降低其辛烷值，进而造成巨大的损失。为了汽油得到最优的利用，在建模过程中研究如何满足操作变量的多样性、对原料分析的高要求及过程优化响应的及时性研究如何在满足汽油脱硫效果的同时( 硫含量不大于5μg/g)，实现降低汽油辛烷值损失在30% 以上。传统的汽油辛烷值测定法采用ASTM-CFR 标准方法对汽油进行分析，操作和维护运行费用高，也有许多研究者采用红外光谱，可用于在线分析、检测成本低等优点，但是得到的操作位点较多，存在许多不确定因素的影响，应用受到一定的限制。目前处理汽油辛烷值的方法可以采用基于统计的方法(如：皮尔森系数、F 值等) 或者基于模型的方法( 如：决策树、随机森林等)，而采用机器学习中基于模型则更加全面分析降低汽油辛烷值的目的。可通过建立相关数学模型来对主要变量进行优化以达到降低辛烷值损失值的目的。针对辛烷值异常数据诊断，可对异常值进行整体修复，但鲁棒性较低；综合前期学者研究，大多针对辛烷值数据修复研究较为分化，没有完整的数据处理体系，模型迁移能力有待提高。针对上述问题，本文提出改进ARMAXGBoost 算法构建出一种综合数据清晰、奇异值、缺失值及异常值处理的辛烷值数据集成处理框架对辛烷值数据进行处理。

2 方法

2.1 数据集及整体处理流程

本文原始数据采集来自某实时数据库。根据所采集到的原始数据进行分析，得到多变量大样本数据（325 个样本、367个操作变量），在原样本中存在一些异常值、缺失值。对本文所用数据提出基于XGBoost 的缺失值填补及基于随机森林的异常值检测算法两种算法方案，整体处理流程如图1 所示。

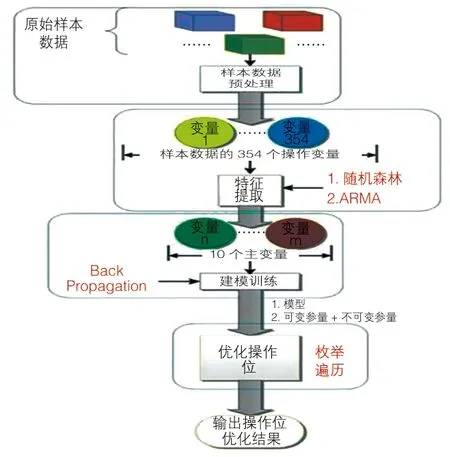
图1 整体框架处理流程

每个样本数据包含两个小时内354 个操作点位记录的实时数据，采样间隔为三分钟。首先对原始数据根据位点操作范围进行阈值筛选，去除在阈值范围外的数据，再对经过筛选的无超纲数据进行缺失值填充。根据位点操作范围对超出范围的数据进行剔除，再通过随机森林模型对点位中的部分缺失数据进行预测填补后，使用随机森林算法对数据中的异常值进行提取，对提取到的异常值传入XGBoost 模型进行修正，最终得到有效性较高的样本原始数据，再对其求均值后，对原样本数据进行替换。

2.2 基于XGBoost 回归模型缺失值处理

缺失值填充方式主要有单变量缺失值插补和多变量联立的缺失值差补，针对存在缺失值的操作位点数据，使用XGBoost回归模型的缺失值预测模型预测的数据填补缺失值。与原始GBDT 相比在代价函数加入正则化项，而且XGBoost 在解决分类问题及回归问题中都具有较好的表现，数据预处理流程如图2 所示。

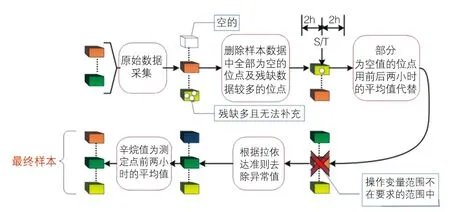
图2 数据预处理流程图

在Boosting 算法中，每次预测结果都和上一次预测结果相关，如（1）式。

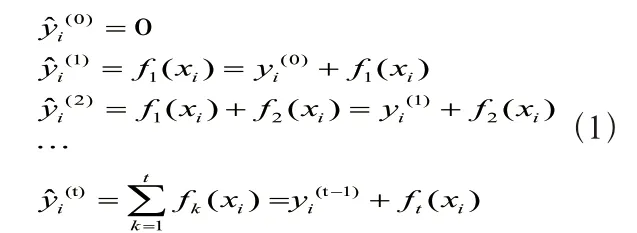
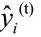
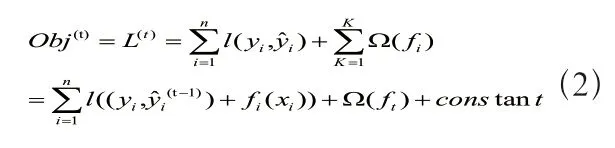
对公式（2）进行泰勒展开得：

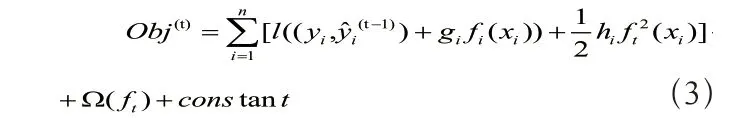
其中，

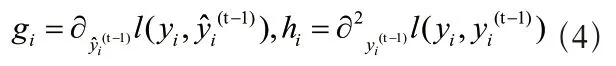
优化 tan项去后得：

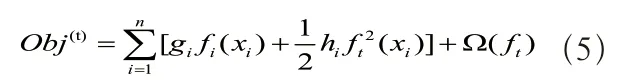
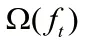
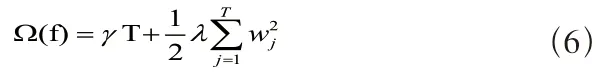
因 为和为复杂度参数。决 定XGBoost 的树是否继续分叉，而控制着正则化的权重。在设置时需要根据实际情况而定。

对公式（6）进一步泰勒展开得到：

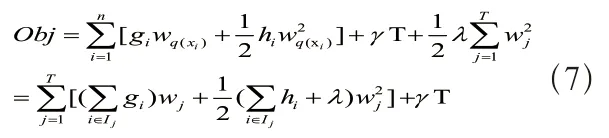
为继续求解，设定：

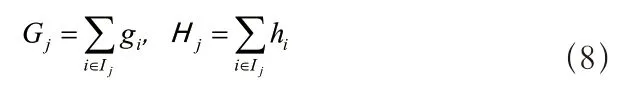
根据公式（8），将（7）转化为：

根据上述公式获得第个叶子的最优值和目标函数的最优解

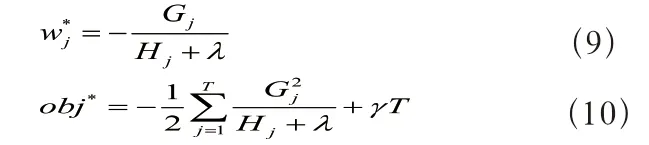
求得最优解后，确定稳定的XGBoost模型。

XGBoost 的改进：关于和值的设定，为避免随机选择不确定性消耗大量运算时间，引入网格搜索算法，将和的可能值作为组合产生网格，结合十折交叉验证方法，对网格中可能的和组成进行搜索优化，获得最优的和组合，从而根据（9）和（10）式快速获得XGBoost 最优解。

2.3 基于辛烷值损失参数的异常值填补模型

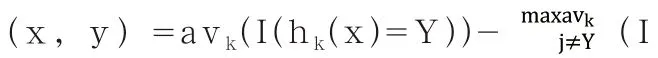
2.4 主要变量特征提取

1）特征提取整体流程

在筛选特征变量之前，对样本数据进行无量纲化处理，避免各变量阈值范围差异过大导致筛选过程中产生影响筛选准确性的噪声。

首先根据拉依达准则，对样本数据中的异常值进行剔除。经过拉依达准则对样本数据中的特征变量异常值进行检测后，部分变量密度曲线及异常值散点图如图3所示。散点图中红点表示异常数据。需对该数据进行剔除。

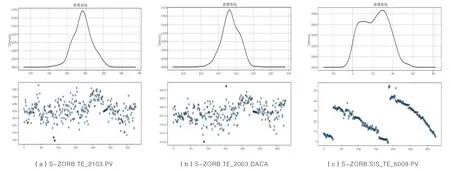
图3 部分变量密度曲线及散点图

图4 特征矩阵构建流程

2.5 自回归滑动平均模型（ARMA）

ARMA 模型曾广泛应用于时间序列的分析和预测，基于其公式计算出未来时刻的最大可能发生的值。尝试利用ARMA 模型来捕获每个操作位的显式和隐式特征属性，每个特征都由一个唯一的参数向量代表，且该向量具备了该特征的序列中的隐含属性，将显式和隐式特征属性均体现在了参数向量中。在建模过程中，可根据具体序列的特性定阶，阶数也是模型参数。利用ARMA 将序列映射到欧氏空间中，并可由其对应的向量唯一确定。为了在后续步骤中提供尽可能多的方法接口，我们在此处引入了图神经网络模型，并以图网络的形式对问题建模。目的在于寻找354 个可变操作位中，对RON 损失影响最大的前n 个操作位，其中各个操作位间具有不同程度的联系和影响，每个操作位可视为一个节点，而操作位间的影响可经过归一化后视为节点间边的权重。依据以上，可将全部样本建模为354+1（354 为可操作变量，1 为目标对象）个节点的完全无向加权图，共325 帧。

利用以上特性，可将多个特征对目标对象的影响程度分析并提取主要特征的问题，转换成对一个维数为（355，325）的图中多个节点的参数向量间影响因子的分析并寻找影响程度较大节点的问题。在此问题中，我们将对各个节点进行图建模，并利用ARMA 对各个节点进行参数向量求取，最后利用参数向量分析出各个节点对目标对象的影响程度。我们设计了算法1来实现该处细节, 算法1 如下所示：

此处，在进行ARMA 建模前还需对原始数据进行判别和整定，对于ARMA 建模，需要进行数据平稳化处理，目的在于剔除掉序列中的趋势项。在此问题中，各个操作位的特征向量均是按照时间序列排成的，所以可能在实际工厂的操作中，会有时间趋势隐藏在操作位的变化中。该处的各个序列具有时间结构，所以对于具有时间结构的序列，完成数据平稳性检测和处理后，即是对节点进行ARMA 建模。此处我们的阶数设置为ARMA（5，0）。确定阶数，即可得到对应数目的参数，并构建参数向量。

最后，根据计算结果，距离目标对象参数向量欧氏距离越近的，影响因子越小，表示对目标对象（产品的RON）影响程度越高。依照此规则，我们确定了10 个操作位，各个操作位与其对应的影响因子。

3 实验结果

图5 为辛烷值预测值与真实值部分数据，模型验证训练神经网络预测模型时，将数据集按4:1 的比例切分为训练集、测试集，该模型在训练集上有非常高的准确率，现对模型进行验证，由于模型在训练集和测试集上都能保持较高的准确率，故认为建立该模型是合理的，该模型具有一定的可行性。如图6 所示为该模型在测试集上进行验证的结果，由图7 可知，用该神经网络预测模型在测试集上进行验证，将产品性质中辛烷值（RON）的预测值与真实值进行线性拟合，拟合系数R 值为0.91315，该拟合系数R 值略低于在训练集上的拟合系数，同样证实该模型在测试集上的效果非常好，预测值与真实值的误差为0.08685。如图7 所示为该模型在训练集和测试集上的综合验证回归参数结果，进行线性拟合所得拟合系数R 值为97.63%，证实该模型在训练集和测试集上的效果较好，预测值与真实值的误差为0.01123。

图5 辛烷值预测值与真实值部分数据

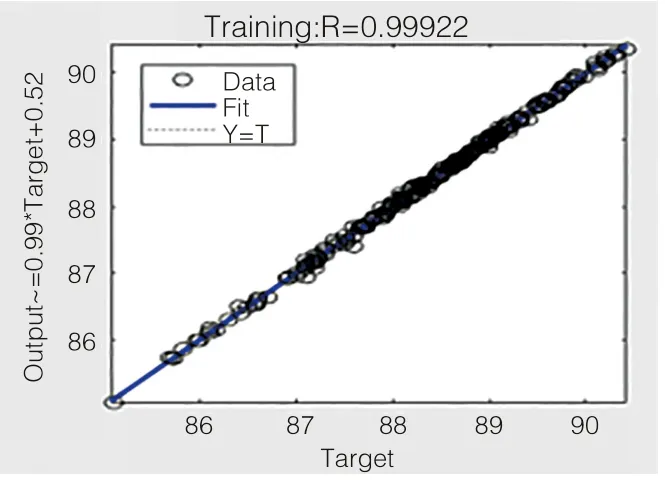
图6 训练集回归参数

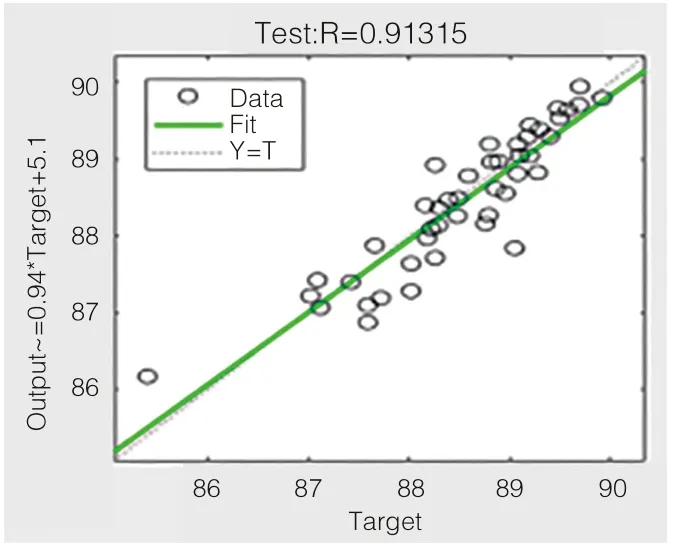
图7 测试集回归参数

由上图验证可知，经过处理后的辛烷值数据集烯烃、芳烃、溴三参数所有值均在正常阈值范围内。综上所述，该神经网络预测模型在训练集上的准确率为0.99922，在测试集上的准确率为91.31%，在训练集和测试集上的整体准确率为97.63%，如图8 所示。最终验证了该神经网络预测模型的合理性与可行性。

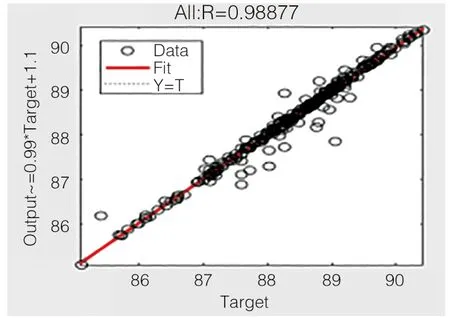
图8 综合验证回归参数

4 结论

本文提出一种改进ARMA-XGBoost算法的辛烷值的异常数据诊断方法，基于ARMA 回归算法的特征提取思路，经过实测数据检验，在训练集和测试集上的整体准确率为97.63%。本文所构建数据处理模型较大程度提升数据利用率，给辛烷值数据的可靠性及有效性提供保证，在未来的研究中对降低实时的辛烷值损失方面进行有效改进提供帮助。