两种方法在不同海拔地区计算湿球温度的对比

周永水 , 原 野 , 石 艳* , 刘 维 , 汤 宁 , 胡兴炜 , 郭 茜

（1. 贵州省气象台, 贵阳 550002；2. 贵州省气象服务中心, 贵阳 550002；3. 贵州省遵义市气象局，遵义 563000；4. 贵州省气象信息中心，贵阳 550002）

引言

湿球温度是指同等焓值空气状态下，空气中的水蒸气达到饱和时的空气温度，它是标定空气湿度的一种手段。湿球温度在采暖通风、空调设计、烟叶烘烤中有较多的应用[1−2]，也是干燥器、冷水塔等工程设计中的重要气象参数[3]。近几年，湿球温度在强对流天气中也得到了较好的应用。俞小鼎[4]指出冰雹的融化层高度更接近于湿球0℃层高度。郑永光等[5]阐述了露点温度和湿球温度的区别。此外，在冰雹大风、雨雪转换等天气过程中，针对湿球温度也开展了较多的工作[6−9]。

早期的地面气象台站是利用干湿球温度表来分别测量温度和湿球温度[10−11]。21世纪以来，随着气象台站自动观测设备的推广和应用，新的观测设备不再观测湿球温度，需要通过其他观测要素间接计算来获得。而对于如何计算湿球温度，气象学者们给出了不同的研究方法，主要以迭代法和逼近法为主[12−14]。已有研究[15−16]指出，最优逼近法的计算结果明显好于牛顿迭代法，但在高海拔地区，逼近法计算的精度比平原地区有所降低，因此，需要对逼近法在贵州等高原地区的适用性进行评估。近年来，以深度学习为代表的机器学习算法飞速发展，并与各类气象大数据有效结合，已成为天气预报[17−18]特别是强对流天气预报的有效手段[19−20]。人工智能等机器学习算法建立在大数据集的应用基础上，利用大量的历史数据进行建模并训练，进而从历史数据中学习规律，通过智能化筛选、组合多种因子进行拟合分类，尤其在多分类拟合等方面有一定的优势，能够处理高维度数据。机器学习算法较多，SMOTE和逻辑回归模型算法[21]、XGBoost集成学习方法[22]、随机森林算法[23]、LightGBM算法[24]、因子分析[25]、深度神经网络算法[26]等在国内强对流天气的预报方面，已经取得了不错的效果。反向传播（Back Propagation，BP）神经网络算法可以逼近任意连续函数，具有很强的非线性映射能力，而且网络的中间层数、各层的处理单元数及网络的学习系数等参数可根据具体情况设定，灵活性很大，所以它在云雷达、微波廓线反演[27−28]、卫星数据反演[29]方面有着广泛的应用，取得了显著的效果。目前，在暴雨诊断模型[30]、加权平均温度模型[31]、电力负荷预测模型[32]的建立方面也有较多的应用，这些应用结果与传统方法相比均有显著的提升。湿球温度和气象因子之间不是简单的线性关系，考虑到BP神经网络算法对非线性关系具有强大的学习能力[32]，本文拟基于BP神经网络构建湿球温度计算模型，并对比其和逼近法在不同海拔地区计算湿球温度的优劣。

1 数据来源和质量控制

本文选取了1990～1999年贵州地区3个国家基准站的逐时湿球温度数据，分别为威宁（海拔2238 m，贵州西部）、贵阳（海拔1295 m，贵州中部）和三穗（海拔626 m，贵州东部）。因贵阳在2000年迁站1次，三穗分别在1982年、2000年迁站，故将3个站点小时数据年限统一为1990～1999年，其中1990～1994年数据用于建立BP神经网络模型和评估逼近法，1995～1999年数据用于检验神经网络模型并与逼近法计算的湿球温度进行对比。BP神经网络模型计算湿球温度的气象要素包括温度、露点、气压、相对湿度和水汽压，所有数据均来自贵州省气象信息中心。当人工观测的湿球温度和前后时次进行对比，在该测站的温度、露点、相对湿度无明显变化而湿球温度出现跃增式变化（变化幅度>1℃）时，认为该数据观测错误，予以剔除。威宁、贵阳、三穗3个站点剔除的数据分别占总数据的13.64%、10.51%、11.5%。

2 逼近法计算湿球温度评估

按照地面气象观测规范[33]，不同观测系统的水汽压公式存在一定差别。使用干湿表温度时的水汽压计算公式如下：

对比逼近法计算的湿球温度和测站湿球温度（表1）可知，威宁、贵阳、三穗3站绝对误差的平均值分别为0.059℃、0.046℃、0.042℃，最大值分别为0.50℃、0.44℃、0.42℃，3站误差的标准差分别为0.09℃、0.07℃、0.07℃。3站中误差<0.1℃的数据比例分别为83.91%、91.52%、92.76%。从一元回归线性拟合结果（图1a～c）来看，逼近法计算湿球温度和测站湿球温度的3站斜率分别为1.0057、1.0057、1.0008，均接近1。3站误差的中位数均为0（图1d），威宁站误差的上下4分位数为0.02、−0.05，上下10分位数为0.05、−0.10；贵阳站误差的上下4分位数为0.01、−0.05，上下10分位数为0.03、−0.09；三穗站误差的上下4分位数为0.02、−0.03，上下10分位数为0.04、−0.08。利用逼近法计算湿球温度与实测值之间的误差很小，总体上看低海拔地区优于高海拔地区。

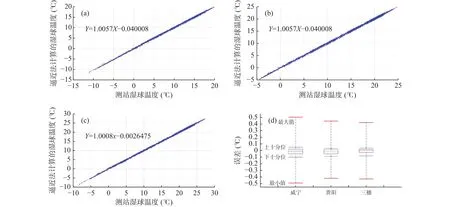
图1 1990～1994年3站逼近法计算湿球温度和实测值的拟合（a. 威宁，b. 贵阳，c. 三穗）及误差（d. 红线由上至下分别表示最大值、中位数、最小值，蓝线表示4分位数，黑线表示10分位数）

表1 1990～1994年威宁、贵阳、三穗站逼近法计算的湿球温度和测站湿球温度的误差

图2给出了逼近法计算威宁湿球温度的误差频次及其与温度、水汽压、相对湿度、本站气压、湿球温度等要素实测值的散点分布。如图所示，大部分误差介于−0.1～0.1℃，>0.2℃的绝对误差出现在温度、水汽压、测站气压和湿球温度的所有区间；当相对湿度<50%时，>0.2℃绝对误差的出现频率很小或近乎为零。当气温<0℃或湿球温度<0℃时，误差有一个明显的增加，这可能和逼近法中对温度的近似处理有关，即当温度高于0℃时，计算过程中按湿球温度表未结冰处理，而低于0℃时，均按湿球结冰计算。而在实际观测中，温度>0℃时湿球有可能结冰，而温度<0℃时也会出现湿球不结冰的情况[16]。根据上述分析可知，威宁海拔高于贵阳和三穗，气温低于0℃的频率高于贵阳和三穗（威宁、贵阳和三穗气温低于0℃的时次在本研究所用数据中占比分别为9.28%、2.12%和1.13%），这就解释了为何逼近法计算的威宁站湿球温度误差>0.1℃数据比例小于贵阳和三穗。贵阳和三穗的误差和温度、水汽压、相对湿度、本站气压、湿球温度等要素对应趋势和威宁相同（图略），因此当相对湿度<50%时，逼近法计算的湿球温度误差均在0.2℃以内。

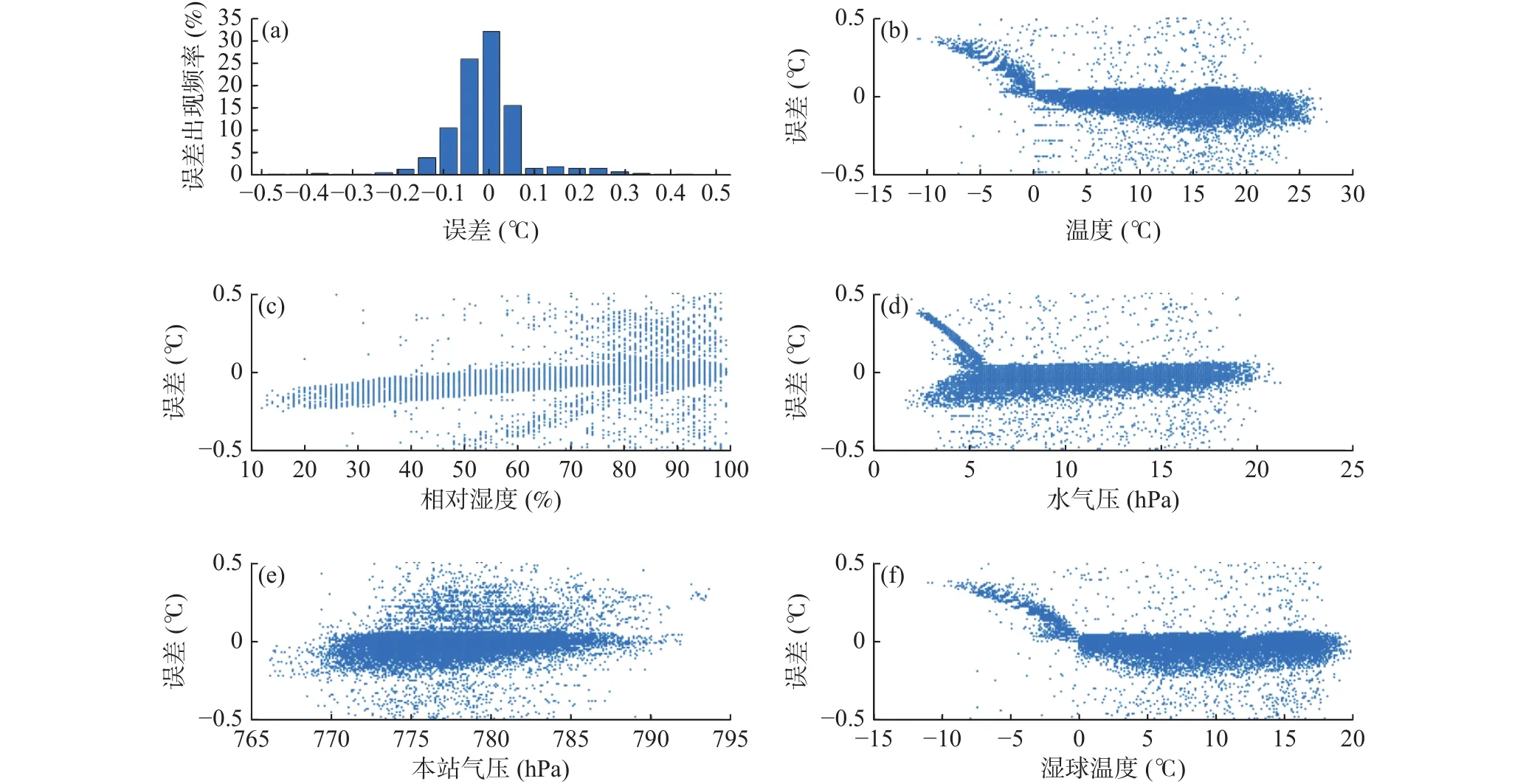
图2 逼近法计算威宁湿球温度的误差频次（a）及其与站点实测要素（b. 温度，c. 相对湿度，d. 水汽压，e. 本站气压，f. 湿球温度）的散点分布

3 BP神经网络拟合方法和逼近法

3.1 BP神经网络拟合过程

本节利用1990～1994年上述3个测站的湿球温度与温度、露点、气压、相对湿度、水汽压共5个参数，基于BP神经网络拟合算法，开展湿球温度计算模型建设。经质量控制后， 1990～1994年3站分别得到25246、39230、38794个样本，其中前70%的样本数据用来模型训练，后30%用于测试和验证；1995～1999年数据将用于检验BP神经网络模型并与逼近法计算结果进行对比，3站数据样本分别为37930、39329、38821个。

)

建模过程中，威宁、贵阳、三穗分别迭代555、336、452次，在迭代次数的前6个节点找到最优解，最优解处的均方根误差分别为0.0035、0.0031、0.0030，均方根误差均低于1×10−2，3站训练、验证、测试和总样本的4类样本回归系数均介于0.9996～0.9997，威宁、贵阳、三穗湿球温度误差分别介于−0.05～0.03℃、−0.11～0.07℃、−0.06～0.03℃（图3）。

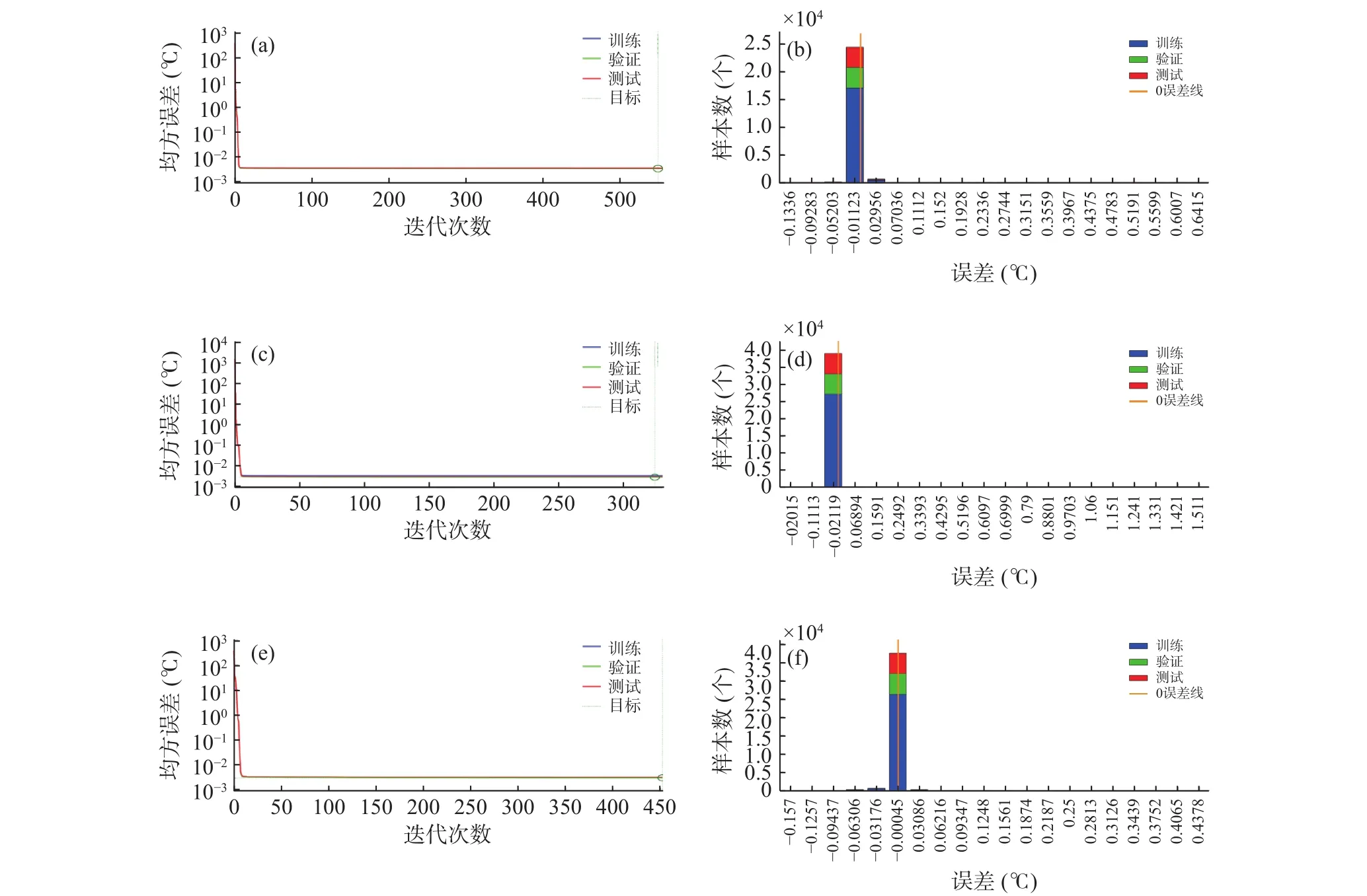
图3 威宁（a、b）、贵阳（c、d）、三穗（e、f）BP神经网络模型收敛效果

3.2 BP神经网络拟合模型和逼近法的对比

利用BP神经网络模型输出1995～1999年湿球温度与站点实测值进行拟合，威宁（图4a）、贵阳（图4b）、三穗（图4c）的拟合斜率分别为0.9996、0.9999、0.9999，确定系数分别为0.9999、0.9999、1.0，均方根分别为0.056℃、0.056℃、0.054℃。利用3站所有数据进行建模，结合威宁基本气象要素，输出1995～1999年威宁湿球温度，并与测站湿球温度进行拟合（图4d），拟合斜率、确定系数及均方根分别为0.9972℃、0.9994℃及0.152℃，均比单站的BP神经网络模型输出的湿球温度拟合效果差。对比BP神经网络模型和逼近法计算的湿球温度（表2）可知，当每个站点均使用单独的BP神经网络模型时，3站BP神经网络模型与观测值的平均绝对误差分别为0.022℃、0.020℃、0.019℃，3站逼近法的平均绝对误差分别为0.056℃、0.047℃、0.045℃，平均绝对误差比逼近法分别降低60.71%、57.45%、57.78%；BP神经网络模型误差<0.1℃的数据比例占比分别为97.38%、97.18%、97.44%，逼近法<0.1℃的数据比例占比分别为85.08%、91.61%、92.54%。综合来看，BP神经网络模型计算湿球温度的精度比逼近法分别提高60.71%、57.45%、57.78%，误差<0.1℃的数据比例分别提高12.30%、5.57%、4.90%。分析逼近法和BP神经网络模型的误差对比箱线图（图5）可知，对于3个站点，两种方法中位线均接近0，BP神经网络模型误差上下4分位数间的数据（盒子）区间比逼近法的数据区间更小，BP神经网络模型误差最大值和最小值的区间也小于逼近法，说明BP神经网络模型计算湿球温度的误差具有更好的收敛性，其效果比逼近法更佳。当使用3站所有数据构建的BP神经网络模型计算威宁湿球温度时，与本站观测值的平均绝对误差为0.106，<0.1℃的数据比例只有59.05%，其效果比逼近法差。总之，通过模型计算，3站误差<0.1℃的数据比例均有上升，威宁湿球温度误差<0.1℃的数据比例显著上升，已完全接近贵阳和三穗，说明通过BP神经网络模型计算湿球温度能有效减少海拔高度增加后结冰现象对计算结果的影响。

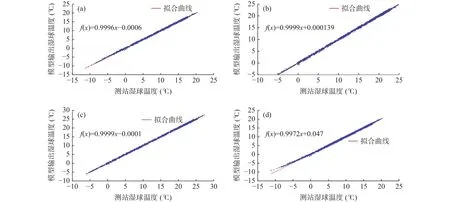
图4 1995～1999年威宁（a）、贵阳（b）、三穗（c）BP神经网络模型输出湿球温度与实测值的拟合结果以及利用3站数据构建模型并结合威宁基本要素输出湿球温度与实测值的拟合结果（d）

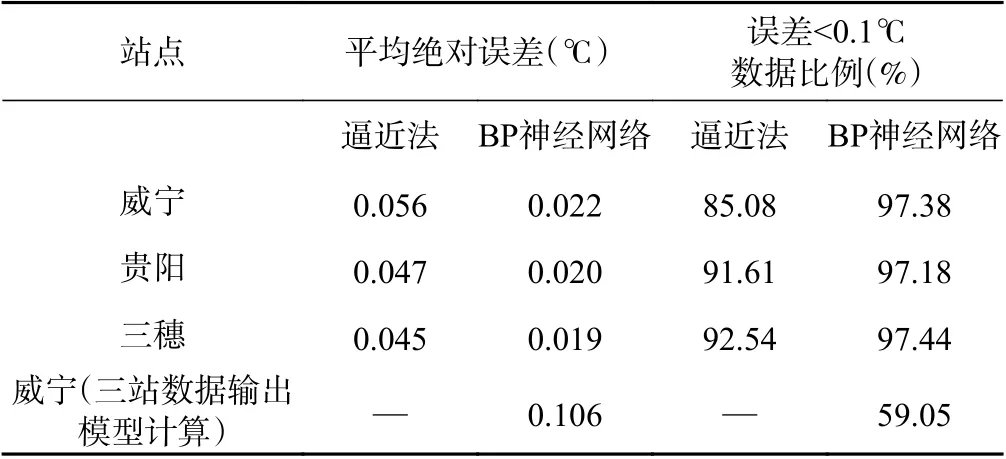
表2 逼近法和BP神经网络拟合结果的平均绝对误差、误差<0.1℃数据比例对比

图5 逼近法和BP神经网络模型计算威宁、贵阳、三穗湿球温度的误差对比

4 结论

利用1990～1994年威宁、贵阳、三穗的温度、气压、相对湿度和湿球温度资料，评估了逼近法在贵州3个不同海拔站点计算湿球温度的效果，通过BP神经网络构建了湿球温度计算模型，对比了BP神经网络模型和逼近法在计算湿球温度方面的优劣，得到如下主要结论：

（1） 对比逼近法计算的湿球温度和实测值，威宁、贵阳、三穗平均绝对误差分别为0.059℃、0.046℃、0.042℃，其中误差<0.1℃的数据比例分别为83.91%、91.52%、92.76，逼近法在低海拔地区的计算结果优于高海拔地区。

（2） 用逼近法计算湿球温度时，误差>0.2℃的频率在气温低于0℃时呈增长趋势，这和逼近法中对结冰的处理方法有关。由于威宁海拔较高，其气温低于0℃的频率高于贵阳和三穗，这也导致逼近法在威宁对湿球温度的计算效果较差。

（3） 对比BP神经网络模型计算的湿球温度和实测值，威宁、贵阳、三穗平均绝对误差分别为0.022℃、0.020℃、0.019℃，模型误差<0.1℃的数据比例占比分别为97.38%、97.18%、97.44%，有效地解决了高海拔地区低于0℃气温频率较高导致逼近法计算误差偏大的问题，在低海拔地区的计算结果也优于逼近法。

（4） 逼近法计算湿球温度所有地区可共用一个公式，而BP神经网络模型计算湿球温度则需要各个测站进行单独拟合，因此，在低海拔地区计算精度要求不高时可用逼近法，反之则需用BP神经网络对每个站点单独建模。