考虑目标同时实现和感知误差的双属性用户均衡模型

孔明珠纪翔峰

(青岛大学商学院管理科学与工程系,青岛 266067)

经济的快速发展促使城市汽车保有量大幅提升,加剧了城市交通运输压力,城市交通拥堵问题成为当前城市发展亟需解决的难题。通过增加道路供给缓解交通拥堵不仅收效甚微,还会耗费大量人力物力,不符合中国集约发展新要求。为此,通过充分研究交通运输系统中出行者的路径选择行为,为交通部门制定相关政策提供理论依据以引导出行者的出行行为,从而减少城市交通拥堵。用户均衡问题是交通运输系统研究中的经典问题,其传统原则是任何出行者均不能通过单方面改变出行路径来减少出行时间,此时即达到用户均衡[1],即出行者在均衡时总会选择出行时间最小的路径。但该原则存在一些不符合实际的假设,如假设出行者的路径选择行为仅受出行时间影响,但研究发现出行者路径选择行为还受出行时间波动性、出行成本等多属性影响[2-4];该原则假设出行者充分了解交通网络的各种信息,而现实中出行者受交通网络不确定性影响,难以获取完整且充分的信息[5]。用户均衡模型通过引入多属性分析,如出行时间和出行成本[6]、出行时间可靠性[7]、出行时间不可靠性[8]等,使假设更符合实际。感知误差的早期研究发现出行者存在感知误差,确定性的出行时间和出行成本会变为随机值,由此提出感知误差初始形式[9];后续研究侧重分析可加形式的感知误差建模[10]和乘积形式的感知误差建模[11]。综上,本文考虑出行者受双属性(即出行时间和出行成本)影响,构建用户均衡模型,采用连续平均算法求解,通过算例验证分析出行者的路径选择行为产生的长期影响。

1 双属性路径效用模型

对于某一路径,假设T表示出行时间,C表示出行成本,εt表示出行时间的感知误差,εc表示出行成本的感知误差,感知出行时间可表示为,感知出行成本可表示为。考虑到感知出行时间和感知出行成本的相互影响,可知间存在随机相关性。给定感知出行时间的可能结果t和感知出行成本的可能结果c,同时基于目标导向型分析方法[12-13],用γt表示出行时间的目标,γc表示出行成本的目标,则效用函数为

当I＝1时,表示两个目标同时实现,即出行者希望出行时间的目标和出行成本的目标能够同时实现。此时,出行者会获得效用且假设该效用为1;否则,出行者未获得效用,设为0。鉴于感知出行时间和感知出行成本的结果均为随机值,则出行者的路径效用为

其中,P()表示联合概率,表示出行时间目标的实现概率(Target Achievement Probability of travel time,TAPt),表示出行成本目标的实现概率(Target Achievement Probability of travel cost,TAPc)。

高斯(Copula)函数用于表示不同因素间的相关关系,已广泛用于交通运输相关研究[12,14-15]。本文利用Copula函数刻画感知出行时间和感知出行成本间的随机相关性,计算其联合概率

其中,u1表示感知出行时间达到目标的概率,即;u2表示感知出行成本达到目标的概率,即;ρu1u2表示感知出行时间和感知出行成本之间的Pearson相关系数,且ρu1u2∈[－1,1] 。若ρu1u2＞0则意味着两者之间为正相关,即感知出行时间的增加(减少)会导致感知出行成本的增加(减少);若ρu1u2＜0则意味着两者之间为负相关,即感知出行时间的增加(减少)会导致感知出行成本的减少(增加);若ρu1u2＝0则表明两者之间不存在相关关系。

2 双属性用户均衡分析

2.1 符号表示

假设一个具有多起点和多终点的交通网络G(N,A),其中N为节点集合,A为连接各个节点的路段集合,R为起点集合,S为终点集合。对于起点r∈R和终点s∈S(即OD 对rs)有以下定义,q rs表示OD对rs间的交通需求,P rs表示OD 对rs间的所有路径,表示路径p∈P rs上的流量。表示路段和路径的关联矩阵。若路径p包含路段a,则,若路径p不包含路段a,则。对路段a∈A,T a表示路段a的出行时间,V a表示路段a的流量,C a表示收费交通网络中路段a的拥堵收费,即路段a的出行成本。基于上述符号和定义,可得

式(4)表示OD 对的出行需求等于所有连接该OD 对的路径流量之和;式(5)表示路段a上的流量等于包含该路段的所有路径流量的总和;式(6)表示路径流量皆为非负值。同时满足上述不等式组的路径流量称为给定交通网络的可行流量。

2.2 均衡条件

其中,上标* 表示均衡状态下的数值。上述均衡问题可表示为变分不等式问题VI(f,Ω),即找到一个向量f*∈Ω,使(f*)T(f－f*)≥0,f∈Ω成立,其中(f*)＝ω(f*)。本文模型中,出行者通过路径选择以实现出行效用最大化,故上式成立。基于变分不等式与均衡条件相关关系研究成果[16-17],由于路径效用是f的连续函数且集合Ω是紧致的、凸的,可知变分不等式存在解,即模型存在均衡解。

2.3 目标设定

出行时间目标值的设定遵循以下原则:出行起点和终点间存在多条路径,首先设定OD 对间出行时间的目标,再设定OD 对间出行成本的目标。考虑出行者的目标导向特性,出行者总希望以其置信水平实现该目标,故OD 对特定路径p上出行时间的目标可表示为机会约束问题,其中θ为出行者的置信水平。作为风险规避的出行者,其置信水平一般较大[7],导致某些路径上的出行时间目标过于保守,即预留时间过长。假设出行者通过选择最优目标以避免出行时间目标过于保守,即,从而得到出行时间的目标。采用相似思想,可得出行成本的目标。

上述出行时间目标设置中,路径p上出行时间的目标采用出行时间预算模型[17],该模型考虑了出行时间和出行时间可靠性,另将均值—超量出行时间模型[18]作为出行时间的目标进行对比,额外考虑了出行时间不可靠性,最终表示为,即出行时间预算的条件概率形式。

3 求解算法和数值实验

3.1 求解算法

采用路径连续平均算法求解上述模型,该算法具有良好的收敛性[18]。

3.2 数值实验

采用图1所示的交通网络测试模型。该网络共有3条路径和5条路段,其中路径1包含路段1和2;路径2包含路径1、3和5;路径3包含路段4和5。OD 对(1,4)间的交通需求为1 500。测试中算法的最大迭代次数为106,收敛率ε0＝10－6,Pearson相关系数为0.7,出行者的置信水平为0.95。路段出行时间t a(v a)采用BPR 函数计算,其中表示自由流时间,C a表示路段通行能力。假设出行时间和出行成本的感知误差均服从正态分布,分别为,则感知出行时间服从正态分布,感知出行成本服从正态分布。若测试中,且当路径出行时间服从正态分布时,出行时间预算为T ＋Φ－1(α)σt,则均值—超量出行时间为从而得到出行时间的目标(表1)。

表1 交通网络测试数据

图1 测试交通网络

在模型中探讨两种出行时间目标下的系统表现,分别从均衡路径流量分布和目标实现概率两方面对比分析(表2、表3)。当考虑出行时间不可靠性时,路径1和路径3上的效用增大,故流量会从路径2转移至路径1和路径3,即出行者会改变其路径选择。同时,均衡TAPc不变,这是由于交通网络上收费是定值;均衡TAPt均增大,这是由于出行时间不可靠性的加入会导致出行时间目标增大。此外,均衡TAPc最大的路径上均衡TAPt一定最小,而均衡TAPt最大的路径上均衡TAPc一定最小,且最大TAPt(或TAPc)为出行者的置信水平。上述实验结果表明当出行者意图同时实现两个目标时,均衡路径的效用会变小。

表2 测试结果(出行时间预算模式)

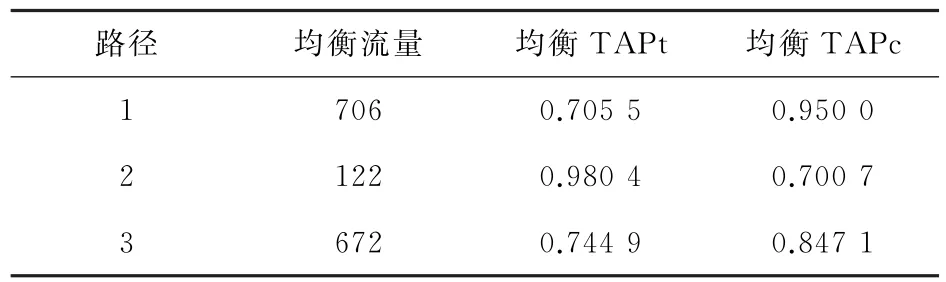
表3 测试结果(均值-超量出行时间模式)

4 结论

本文构建用户均衡模型讨论出行者路径选择行为产生的长期影响。所提路径选择模型考虑了出行者感知误差的存在和出行者的目标导向特性,拓展了已有研究的范畴。通过对比研究出行者不同风险规避特性对系统表现产生的影响,揭示了出行者目标导向行为特征下的流量分布及目标实现情况。出行时间目标实现概率均衡值最大的路径上,出行成本目标实现概率均衡值最小;当两个目标同时实现的概率增大时,均衡路径上的效用会变小,反之亦然。由于本文中交通网络的拥堵收费是给定的,今后可基于该研究结果探讨最优拥堵收费问题。