自动化码头出口箱箱位分配优化超启发式算法
2022-09-05黄子钊庄子龙
黄子钊,庄子龙,滕 浩,秦 威+,秦 涛,邹 鹰
(1.上海交通大学 机械与动力工程学院,上海 200240;2.上海海勃物流软件有限公司,上海 200080;3.上海国际港务(集团)股份有限公司,上海 200080)
0 引言
近年来,在集装箱码头领域,随着自动化设备、人工智能算法等技术的不断发展,自动化集装箱码头在提高码头整体作业效率、降低劳动力成本等方面逐渐形成明显优势,已成为未来的发展趋势。然而,由于规模庞大、业务复杂、现场操作人员少等特点,自动化集装箱码头的作业效率还存在较大的提升空间,急需更高效的计划调度方案。其中,在关系到船舶停靠时间即码头效率的出口箱装船作业中,自动化集装箱堆场由于箱区垂直于岸边、交互区位于箱区两侧、场桥冲突等约束的存在,以及出口箱需要从陆侧入场、从海侧出场导致的场桥操作距离较大的状况,难以取得较合理的决策,是出口箱作业效率提升的瓶颈所在。在堆场作业中,出口箱的箱位分配是堆场优化的基础和关键,方案的优劣直接影响到了堆场的吞吐能力,进而影响出口箱装船作业的效率。但是,由于问题规模较大、动态性较强、约束较多等特点,目前实际采用的箱位分配方案难以满足任务平衡、翻箱率低等要求,制约了作业效率的提升。因此,研究自动化集装箱码头出口箱箱位分配问题对提高出口箱整体作业效率具有重要意义,已受到学者们的持续关注。
在自动化集装箱码头出口箱箱位分配问题中,现有研究按研究尺度可以分为箱区或倍位分配以及具体箱位分配两种。在箱区或倍位分配中,LIANG等[1]考虑一个作业路上的任务,基于最小化集装箱移动距离,建立了混合整数规划模型,并采用混合的遗传算法展开求解;JIANG等[2]以最小化成本,即可预计的场桥移动操作成本及翻箱成本为目标,开发了分支定界方法展开求解,得到了每个任务的目标倍位;梁承姬等[3]针对一个箱区,以负载均衡为目标,设计了基于网络流的禁忌搜索算法,通过与精确求解算法展开对比,证明了算法的有效性;YANG等[4]考虑到经济方面的约束,以最小化成本和最大化利润为目标,基于遗传算法针对每个任务指派对应的倍位和机械资源;靳志宏等[5]考虑到外集卡提前预约入场的现状,为了让箱区负载均衡,建立了数学规划模型并使用CPLEX进行求解,结论表明预约信息对作业均衡有20~30个百分点的帮助;倪敏敏等[6]考虑到场桥同时作业的影响,采用分区域动态平衡的方法减少场桥的无效作业时间,提高堆场效率;韩笑乐等[7]考虑泊位与堆场的相互影响,设计了改进的遗传算法得到不确定环境下的箱区和泊位分配方案,实现了鲁棒性调度决策。
在具体箱位的分配中,CARLO等[8]综述了早些年针对箱位分配问题的研究,其中求解方法可以分为先执行箱区和倍位分配后执行具体箱位分配的两阶段方法和通过混合操作一步得到完整分配方案两大类,通过对比发现后者的性能优于前者。近五年来,BOYSEN等[9]针对一个倍位的堆存范围,以最小化翻箱为目标,定义了箱位分配问题的下界,并证明了可以在n3时间复杂度内精确求解;GOERIGK等[10]考虑到箱位分配会对场桥调度有直接影响,以最小化箱位冲突为目标,建立了破坏和重建的局部搜索方法;曾建智等[11]引入后期机械资源调度的约束,开发了双层遗传算法同时解决箱位分配与资源调度问题;周鹏飞等[12]也考虑了外集卡的不确定性,基于目前码头已有的预约信息,使用了基于图的禁忌搜索算法,较确定性模型取得了十余个百分点的提高;SHEN等[13]针对一个倍位的箱位分配问题,考虑到问题时间要求较高,在同一种环境下应用机器学习方法,采用堆场现状作为状态,目标箱位作为动作,方案的可行性作为回报,并采用随机数据进行训练和验证,得到了符合实际的分配方案;李隋凯等[14]针对出口箱箱位分配,引入接力操作,采用动态规划方法快速得到了较好的解;CHANG等[15]考虑箱区负载均衡以及箱位冲突最小的目标,开发了基于模拟退火框架的两阶段调度模型,得到完整的箱位分配方案;MALDONADO等[16]基于集装箱在港口的停留时间,开发了箱位分配模型,从而减少可预见的翻箱操作。
总之,在箱位分配问题中,当前的一部分研究更多关注具体箱位的选取,并采用精确求解、调度规则或智能算法加以解决。另一部分研究则关注箱区或倍位的选择,通过和其他问题的集成形成全局中更好的方案。然而,由于自动化集装箱码头出口箱箱位分配问题具有较大规模和难度,当前的解决方案还不能满足码头整体高效作业的需要。同时在当前研究中,较少考虑实际自动化集装箱堆场的接力、多箱区协同等特性,且方案效果还有较大的提升空间。基于这一现状,本文提出一个考虑实际场景中上述两个特性的出口箱箱位分配问题模型,从而确定具体箱位,使后续翻箱率最低。之后,本文提出一种新颖的基于强化学习的超启发式算法用于解决这一问题,得到高质量的箱位分配方案,提高自动化集装箱码头出口箱作业的作业效率。
1 问题描述
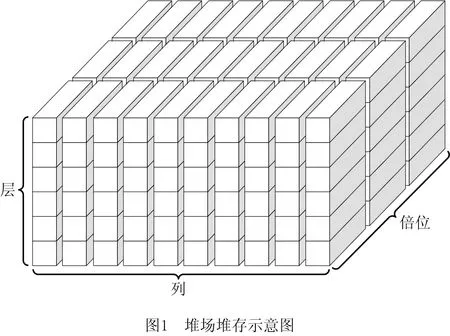
如图1所示为自动化集装箱堆场堆存的示意图,自动化集装箱堆场可以划分为数十个箱区,每一个箱区由若干个倍位组成,每个倍位由数列和数层构成。在自动化集装箱堆场中,通常一个箱区包含50个倍位,一个倍位由10列和6层组成,即一个箱区包含3 000个集装箱箱位,具有极大的规模。
如图2所示为典型的自动化集装箱堆场的示意图。区别于传统集装箱堆场,为满足自动化区域与人工区域的分离,自动化集装箱堆场与自动导引小车(Automated Guided Vechicle,AGV)和外集卡的交互集中于箱区两侧,而不像传统堆场那样可以在箱区边缘任意地方。同时,自动化集装箱堆场使用轨道吊沿着既定的轨道执行操作,不能相互跨越和在多个箱区间移动。因此,为了最大化工作效率,一个箱区中通常会配置两台场桥,服务于海侧和陆侧两个交互区。
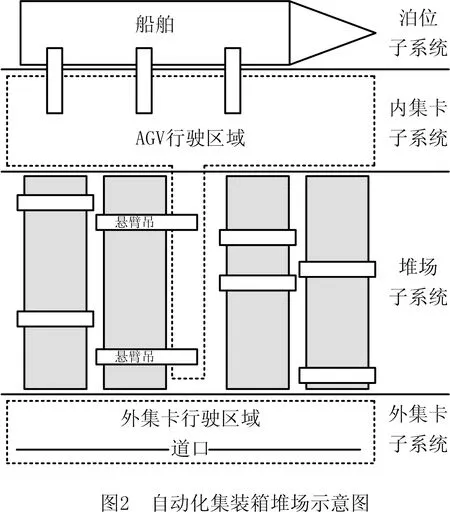
基于上述特点,自动化集装箱堆场箱区的吞吐能力的上限较低,单个箱区难以满足短时间内密集的出口箱运输任务。在此情境下,为了最小化任务延期时间和最大化工作效率,自动化集装箱堆场采用多箱区协同的方式,打破传统堆场按类别放置集装箱的原则,将同时段同泊位的集装箱分散于数个箱区中,尽可能使得各个箱区的任务负荷相当,从而发挥箱区数量大的优势,满足出口箱运输需求。另外,基于出口箱海侧任务密集的特点,为了使吞吐能力满足需求,堆场引入了悬臂吊设备,能够与AGV在箱区侧面展开交互,减小场桥移动距离,提升箱区海侧交互能力。这些方式虽然具备更高的效率,但极大地提高了问题的复杂性,对堆场的计划调度提出了更大的挑战。
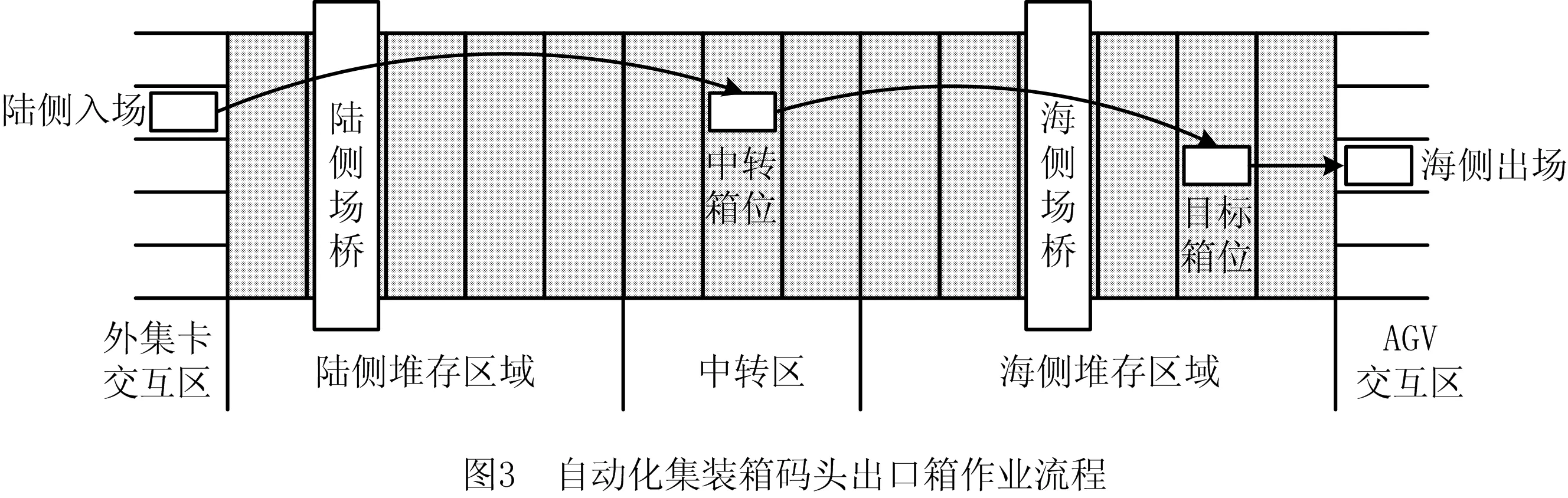
在出口箱作业中,集装箱由外集卡运输进入堆场,经过陆侧入场作业、堆场存储、海侧出场作业3个阶段,最终由海侧经AGV运输离开堆场,整体的作业流程如图3所示。在这一流程中,由于自动化集装箱堆场的长度较长、场桥无法相互跨越,若由单一场桥执行入场和出场作业,会使作业区间较大,极大影响到另一台场桥的作业,导致整体效率偏低。因此,自动化集装箱堆场设计了较为复杂的接力操作,即两台场桥配合执行一项出口箱的入场任务。首先在堆场中部设立了中转区用于出口箱接力操作,其次针对出口箱制定中转箱位,由陆侧场桥将出口箱从外集卡转移至中转区,之后由海侧场桥由中转区移动至海侧的目标箱位。由于集装箱堆叠的一系列原则,中转区的箱位选择需要尽可能均衡,从而减少阻塞情况。
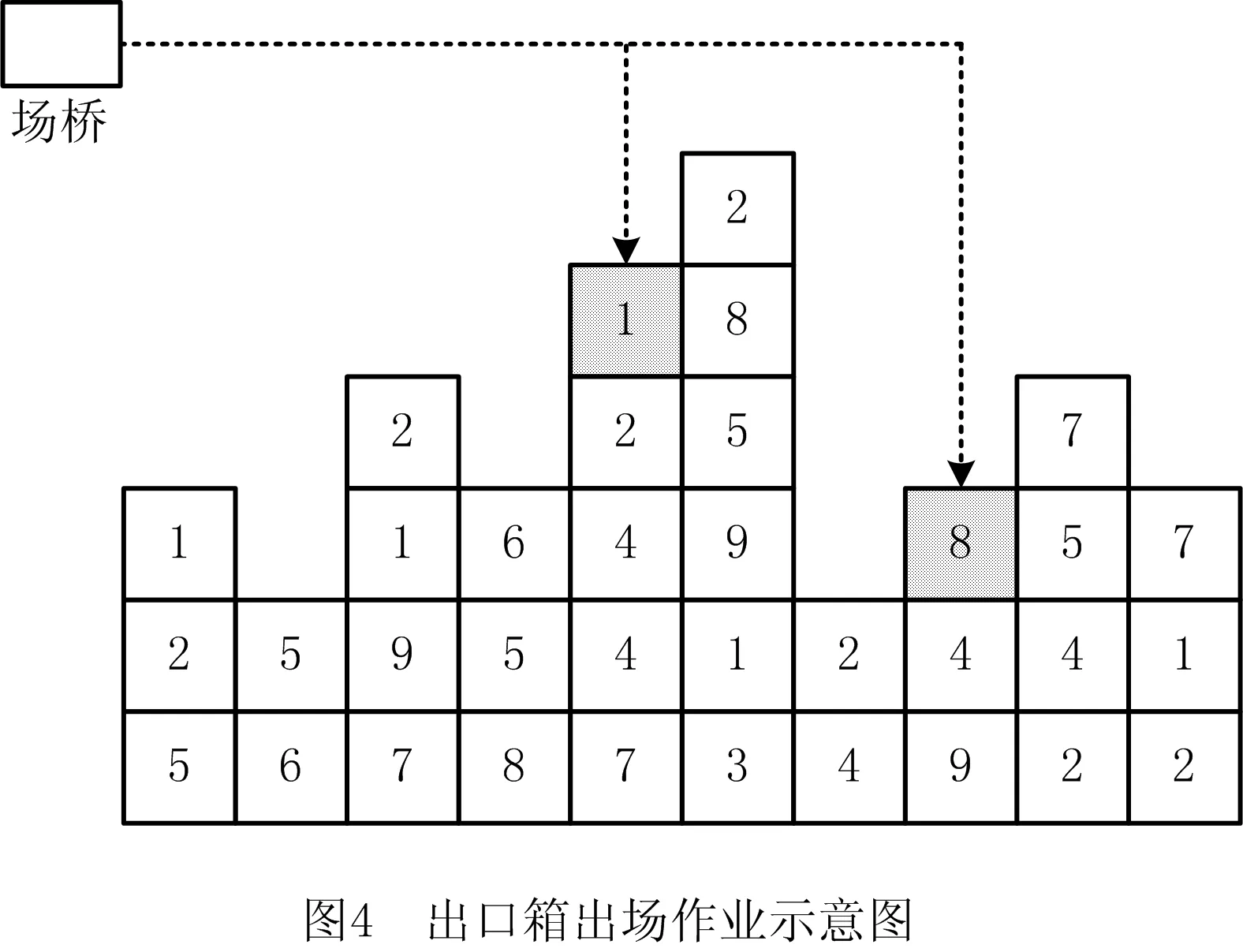
由于自动化集装箱堆场是一个三维环境,在出口箱出场作业中,若目标集装箱不在最顶层,则会产生压箱,需要先将上方的集装箱翻倒再执行出场作业。图4列出了一个倍位的出场作业截面图。假设当前时刻为0,图4中集装箱的数字为根据船舶配积载和AGV计划得到的出场时间,数字越小说明出场越早。在出口箱入场作业时,若该集装箱的出场时间晚于其下方集装箱的出场时间,则产生压箱,后期需要执行一次翻箱操作。以图4所示出口箱为例,灰色出口箱1下方没有早于该箱的集装箱,因此无需翻箱;而灰色出口箱8下方集装箱的出场时间要早于该箱,需要翻箱,影响了作业效率。经统计,在自动化集装箱堆场中,翻箱操作已成为制约堆场作业效率的最主要因素,需要在出口箱箱位分配时予以着重考虑。
由上述分析可知,在自动化集装箱码头出口箱作业中,由于问题规模较大、堆场空间及场桥的约束较多、多箱区、悬臂吊、接力和压箱等特点,出口箱箱位分配问题具有较大的挑战。因此,本文以出口箱箱位分配问题为研究对象,以平衡箱区和中转区的负载以及最小化后续翻箱操作为目标,对出口箱的箱区、中转箱位和目标箱位的指派进行优化,达到堆场高效处理出口箱任务的目的。
2 问题建模
由于自动化集装箱码头不断运行,出口箱任务的入场出场等信息需要通过预测等手段得到,存在一定的误差,且该误差会随着时间的推移逐渐累积,继而影响最终方案的性能。因此,需要引入实时修正的求解方法。基于这一特点,本文采用滚动计划考虑一个时间窗口内的出口箱箱位分配问题,即每次考虑之后一段时间内的箱位分配问题,并在实际采用前一部分方案后,重新针对后一部分以及之后一段时间内新的箱位分配问题进行分析,在获取了新的出口箱信息的情况下,尽可能减少上述误差。具体模型如下:
2.1 问题假设
(1)由于箱区与泊位存在多对一的关系,考虑一个泊位对应的数个箱区的箱位分配问题。
(2)每个箱区中场桥设备是否为悬臂吊的情况已知,且不考虑设备的故障。
(3)每个出口箱的陆侧入场时间、海侧出场时间均已知。
(4)堆场初始堆存状态以及已堆存的出口箱出场时间已知。
(5)本文考虑相同规格的集装箱,以20尺集装箱为标准,即一个箱位堆存一个集装箱。
(6)本文不涉及冷藏箱、危险箱等特种箱,仅考虑普通箱的堆存。
2.2 符号定义
2.2.1 参数
I为按入场顺序排列的出口箱集合,I={1,2,3,…,NI},通过i,j索引;
E为出口箱后续出场时间集合,E={1,2,3,…,NI};
A为泊位对应的箱区集合,A={1,2,3,…,NA},通过a索引;
W为泊位对应的箱区的权重集合,W={1,2,3,…,NA};
BT为箱区内中转区的倍位集合,BT={1,2,3,…,NBT},通过bt索引;
BG为箱区内海侧堆存区域的倍位集合,BG={1,2,3,…,NBG},通过bg索引;
R为倍位内列的集合,R={1,2,3,…,NR},通过r索引;
T为倍位内层的集合,T={1,2,3,…,NT},通过t,ta,tb索引,其中t代表一个出口箱,ta,tb代表两个不同的出口箱;
TC为堆场中中转区已堆存的集装箱集合,TC={1,2,3,…,NTC},通过tc索引;
PTCtc,a,bt,r,t=

GC为堆场中海侧堆存区域已堆存的集装箱集合,GC={1,2,3,…,NGC},通过gc索引;
EC为堆场中海侧堆存区域已堆存的集装箱出场时间集合,EC={1,2,3,…,NGC};
PGCgc,a,bg,r,t=

2.2.2 过程变量
ybi,j,a,bg,r,ta,tb=

yci,gc,a,bg,r=

zbi,j,a,bg,r,ta,tb=

zci,gc,a,bg,r=
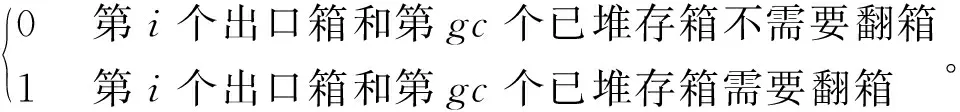
2.2.3 决策变量
xai,a,bt,r,t=

xbi,a,bg,r,t=
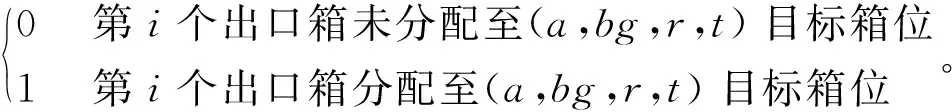
2.3 模型构建
minf=f1+f2+f3,
(1)
(2)
(3)
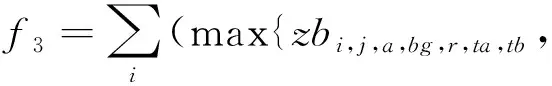
(4)
s.t.
(5)
(6)
(7)
(8)
(9)
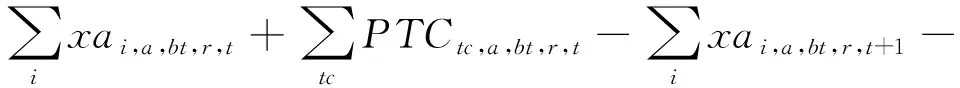
(10)

(11)
ybi,j,a,bg,r,ta,tb≥xbi,a,bg,r,ta+xbj,a,bg,r,tb-
1,∀i,j,a,bg,r,ta>tb;
(12)
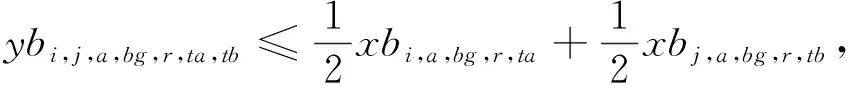
(13)
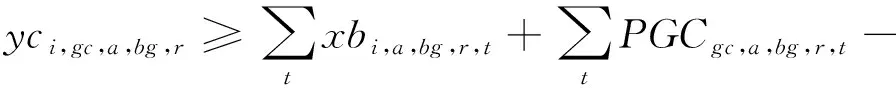
(14)
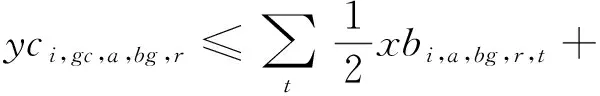
(15)
(16)
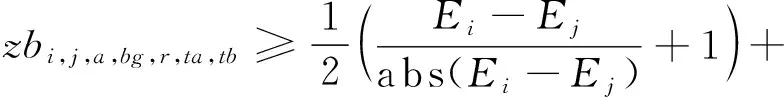
(17)
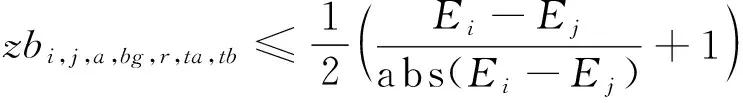
(18)
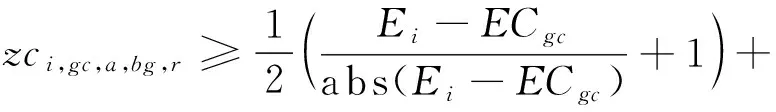
(19)
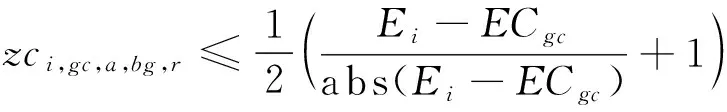
(20)
模型的目标函数如式(1)所示,表示最小化箱区负载不均衡度、中转区负载不均衡度和后续翻箱数量的总和。式(2)通过箱区任务数量带权重的标准差表示箱区负载不均衡度;式(3)通过各个箱区中转区各列任务数量的标准差表示中转区负载不均衡度;式(4)表示需要翻箱的集装箱数量。目标中翻箱率的权重较高,体现翻箱数量的重要性。式(5)~式(20)为约束条件,其中式(5)~式(7)表示每个出口箱对应一个箱区、一个中转区箱位和一个目标箱位。式(8)~式(9)表示每个箱位对应一个集装箱;式(10)~式(11)表示集装箱不能悬空堆存;式(12)~式(15)判断了出口箱之间以及出口箱与已堆存集装箱是否在同一列;式(16)表示先入场的集装箱不能摆放在后入场的集装箱上方;式(17)~(20)判断了出口箱是否摆放在更早出场的集装箱上方,即该出口箱是否需要被翻箱。
基于这一问题模型可以看出,在本文研究的自动化集装箱堆场出口箱箱位分配问题中,在本研究的问题假设下,实际问题具备数百任务上千箱位的规模,且过程与决策变量包含多个维度,难以求解。其次由于堆场交互设备较多并且场桥效率有限,需要引入多元的评价方式以平衡各类设备的影响,最大化整体的作业效率。最后,基于三维码放、场桥接力、悬臂吊等特性,问题模型具备了较多种类的约束,极大地增加了有效方案的生成难度。因此,研究的问题具备多维度评价、约束复杂、规模极大、决策变量较多等特点,从而导致了较高的求解难度。鉴于此,本文引入新颖且高效的基于强化学习思想的超启发式算法,以期取得较好的箱位分配方案。
3 算法设计
由于本文研究的问题规模极大、约束较多,求解十分复杂,常用的启发式规则、智能优化算法难以获得较满意的箱位分配方案,需要引入更高效的优化算法,提高求解方案的性能。本文开发了基于强化学习思想的超启发式算法(Reinforcement Learning based Hyper-Heuristic,RLHH),能够充分利用各种不同启发式算法的优势。算法可以分为低层算法和高级控制策略两个层级。在低层算法中,本文针对问题的特点和可能出现的不同情况引入了多种传统的和新近开发的启发式算法,尽可能地扩大算法适用的场景范围。在高级控制策略中,本文采用了更为新颖的基于策略的强化学习算法DPPO(distributed proximal policy optimization),根据迭代以及场景状态智能选取合适的启发式算法。在强化学习算法中,本文主要使用了用于加速训练测试过程的A3C多线程方法以及用于更快收敛策略梯度的自适应学习率[17,18]。此外,由于深度学习能够提供更大的状态空间和更好的性能,本文应用这一技术来计算策略梯度。本文采用算法的原理、流程以及重要的模块如下所述。
3.1 算法原理
自超启发式的概念被提出以来,它已成为了一种用于合成多种算法的高效的技术。超启发式算法是一种特殊的搜索方法,它从一系列预定义的启发式方法中选择或生成新的启发式方法,而不是直接解决问题[19]。因此,它可以被视为一种高层的算法,自动生成适当的启发式算法组合,从而有效地解决问题[20]。近年来,有许多研究集中在该领域,并将这一方法应用于不同的问题,取得了一定的成果[21-24]。
在超启发式算法的框架中,一个关键点是如何高效地在启发式方法空间中开展搜索,选择最恰当的启发式算法。为解决这一问题,人们引入了强化学习方法。强化学习作为一种强大的决策工具,近些年已引起了广泛关注,在许多领域取得了可喜的成就[25-27]。强化学习方法能够在给定情况下智能选择接下来应采取的行动,并通过与环境的交互来获得最大的回报。在超启发式算法框架中,这一方法能够满足高层控制决策的需求,形成更好的算法[28-30]。但是,当前绝大多数应用还仅限于基于价值的强化学习,而几乎没有基于策略的强化学习方法。由于基于价值的强化学习可能具有对问题的描述能力有限和难以适应随机策略的缺点,并且在启发式算法空间中对这两个方面的要求较高,本文使用基于策略的强化学习方法来进一步提高性能。
3.2 算法流程
在RLHH算法中,算法首先对当前问题的输入进行处理,得到当前问题矩阵化的表征。其次,算法初始化了不同的启发式算法以及相应的种群。然后,算法根据得到的种群以及当前问题的特点对强化学习的状态参数进行计算,并应用DPPO算法得到当前的策略梯度,从而确定下一步采取的启发式算法。之后,算法应用选定的启发式算法开展迭代,不断优化问题的解决方案,并生成优化后的种群。最后,不断重复上述两步,直到满足终止条件。整个算法的伪代码如算法1所示。
算法 1RLHH()。
输入:堆场中已有的集装箱及其出场时间yard,时间窗口内的出口箱任务task;
输出:算法模型或箱位分配方案。
begin
1: 初始化更新前后的演员网络actornew(),a_para, actorold(),a_paraold; 初始化评论家网络c_para
2: 初始化不同的启发式算法 LLH[i],i=1, 2,…, m
3: 初始化算法参数,包括最大回合数episodemax,回合中的最大步数dmmax,批尺寸batchmin
4: if当前过程是训练过程then
5: 初始化中心线程tc, 初始化多个工人线程twi,i=1, 2…wn和线程同步变量mutex
6: 状态、动作和汇报缓存sb,ab,rb← empty
7: fornum← 1 toepisodemaxdo
8: fork← 1 towndo
9: //下面是工人线程twk流程
10: 随机生成新的问题status,outbound,toutandtin←yard,task
11: 群体x[i]← Rand (),i=1, 2,…,P,P为群体中个体数量
12: 个体最优值ibest[i]←x[i],i=1, 2,…,P
13: 状态s←x的评分和个体差异
14: fori← 1 todmmaxdo
15: 策略梯度w← actornew(s)
16:a,snew,r← ApplyAction(w,I, LLH)
17:s←snew
18:sb←sb+s
19:ab←ab+a
20:rb←rb+r
21:tmax← length ofrb
22: iftmax>batchminthen
23: //下面是中心线程tc流程
24:mutex,a_para,a_paraold,c_para← TrainNetwork(mutex,a_para,a_paraold,c_para)
25: end
26: end
27: end
28: 算法模型←a_para,c_para
29: return算法模型
30:else
31: 问题环境status,outbound,toutandtin←yard,task
32: 群体x[i]← Rand (),i=1, 2,…,P
33: 个体最优值ibest[i]←x[i],i=1, 2,…,P
34: 状态s←x的评分和个体差异
35: fori← 1 todmmaxdo
36: 策略梯度w← actornew(s)
37:a,snew,r← ApplyAction(w,I, LLH)
38:s←snew
39: end
40: 最佳个体编号best← 评分最高的x的编号
41: 箱位分配方案 ←x[best]
42: return箱位分配方案
end
3.3 超启发式算法设计
为了进一步提高算法的求解性能,本文设计了一种新颖的超启发式算法。算法中主要包含了问题映射、低层启发式算法以及高层强化学习控制策略3个关键部分。问题映射主要解决低层启发式算法与高层强化学习算法之间的环境定义与计算以及本文解决的箱位分配问题与启发式算法之间的编码与解码流程;低层启发式算法主要包含用于求解箱位分配问题的多种局部搜索算子、全局搜索算子以及智能算法,形成备选的启发式算法库;高层控制策略主要包含针对问题特点设计的强化学习方法,算法具体内容将在3.4节中详细阐述。
3.3.1 问题映射
在RLHH算法中,主要包含3个层面的内容:高层强化学习决策算法、低层启发式算法以及出口箱箱位分配问题。其中,前两个内容主要依靠强化学习的环境作为桥梁。由于高级策略只能从环境中学习问题及其变化历史,这一环境应当包含低层算法的所有特征。由于强化学习算法将从选择的启发式算法的迭代过程中学习,特征是启发式算法的种群及其得分。另外,为了更方便地调用特定的低级启发式方法,环境中还包括了种群中每个个体的最佳历史记录及其分数。
另一方面,后两个内容之间需要依靠特定的编码和解码方式来连接。在RLHH中,采用了箱位坐标的方式进行直接编码,即每一个出口箱任务具有箱区、中转箱位和目标箱位3个数值。其中具体箱位采用层次编码形式,即按倍位、排的顺序依次给每个箱位一个数值,并将出口箱将放在这一排的最上方,如图5所示。例如(2,62,125)为一个出口箱的箱位分配结果,包含3个数字,其中第一个出口箱的箱位分配结果,这一出口箱分配给第2箱区,中转箱位为第7倍位、第2排,目标箱位为第13倍位、第5排。

3.3.2 低层启发式算法
针对上述编码方式,算法将在解码流程中通过模拟的方式计算出每个出口箱的具体位置,之后计算目标函数。由于编码没有限制目标箱位的可行性,在启发式算法中需要引入个体修复策略满足问题需求。同时,为了提高算法运行性能,个体修复策略将会在个体解码的流程中开展应用。在模拟过程中,当某一出口箱的目标箱位所在排已经堆存了6个集装箱,即没有多余空间堆存当前出口箱时,算法将自动就近选取空闲的箱位并将其分配给该出口箱,同时对这一个体进行修改,防止后续迭代过程中再次计算,减小计算量并提高种群中个体的质量。
为了提高RLHH算法的性能,算法中采用了局部和全局搜索算子以及智能算法组成低层启发式算法库。其中,任务不平衡性仅取决于出口箱的码放区域,但翻箱率指标取决于堆存现状以及出口箱具体的码放方案。为此,在算法中引入了不同的局部搜索算子,修改一个或数个出口箱的码放位置,在不大幅改变任务不平衡性的基础上尽可能获得更小的翻箱率。基于全局优化的考虑,引入不同的全局搜索算子修改一部分出口箱的码放位置,从而跳出局部最优方案。最后,引入研究中常用的且性能已获得实际验证的智能算法,进一步提高算法性能。算法中使用的启发式算法及其简要描述如表1所示。

表1 低层启发式算法
3.4 强化学习算法设计
由于常规方法难以根据不同问题合理地选择不同低层启发式算法,取得良好的性能,本文引入基于策略的DPPO强化学习方法作为高层决策算法,以期得到满意的算法性能。考虑到应用强化学习的一项重要条件是问题的决策过程具备无后效性,即某阶段的状态一旦确定,则此后过程的演变不再受此前各状态及决策的影响,本文首先针对问题特点进行了分析。针对高层决策算法这一模块,考虑的是如何合理应用不同的低层启发式算法来改进当前箱位分配问题的解。一方面,在低层启发式算法改进的过程中,基于搜索算子和智能算法的定义,算法仅考虑当前求解方案的编码以及对应的评价指标,采用不同策略修改编码并提升指标,而与求解方案的历史变化无关。另一方面,在选择合适的低层启发式算法时,考虑到上述改进措施的特点,相关历史信息不会对算法的迭代造成影响,因此算法也仅需考虑当前种群中各个求解方案的编码以及指标,从而满足决策过程的无后效性。在满足应用强化学习条件的基础上,本文针对问题以及低层启发式算法的特点有针对性开发了状态、动作、回报、神经网络结构和训练策略等模块。
3.4.1 状态
在算法迭代过程中,启发式算法对种群进行更新后,强化学习策略都会计算环境状态,指导下一步的迭代。由于在不同的种群状态即质量与分散程度下不同的启发式算法存在性能差异,算法采用了个体得分和个体差异性作为状态内容,即s= {f,d}。其中:f是归一化的种群中每个个体的得分,即当前箱位分配方案的目标函数值,其大小为1×n,且n为个体数量;d表示所有个体之间的差异,为一个n×n的矩阵,且每个数字dij由式(21)得到,表示种群中indi和indj之间的差异性。
(21)
3.4.2 动作
在强化学习的学习和运行过程中,需要在每个决策时刻选择下一步迭代的启发式算法。因此,本文中强化学习算法的动作为特定的启发式算法,以a= {0,1,2,…,m}表示,其中m为启发式方法的数量。此外,本文采用ε-贪婪的方法来平衡动作选取的探索和利用,在不同情况下选择正确的行动。在每个决策时刻,算法会根据之前计算得到的不同动作的策略梯度进行动作选择。算法会生成一个随机数,若该数字大于固定概率ε(0≤ε≤1),则将贪婪地选择动作,即选择策略梯度最大的那个动作;否则,算法将随机选择动作。其中该参数采用研究中常用的0.8,平衡贪婪与随机选择之间的比例。选择了下一步的动作后,选定的启发式算法将更新种群,并连续运行几代,以消除随机误差。另外,为了更高效地运行启发式方法,算法保留了每个个体各次迭代中的最优值,记为ibest。最后,算法将计算新的状态和奖励用于后续迭代与网络训练。动作选择和应用的伪代码如算法2所示。
算法 2ApplyAction()。
输入:策略梯度w,当前决策时刻序号i以及低层启发式算法LLH;
输出:动作a、新的状态snew和回报r。
begin
1:temp← Rand (range =[0,1])
2: iftemp> 0.8 then
3: a←Randint (range =[0, m -1], weight =w)
4: else
5:a← Randint (range =[0, m -1])
6: 选择的启发式算法MH← LLH[a],并初始化运行代数genmax
7: 新的种群xnew←x
8: 新的个体最优值ibestnew←ibest
9: forj← 0 togenmaxdo
10:xnew,ibestnew←MH(xnew,ibestnew)
11:end
12:x←xnew
13:ibest←ibestnew
14:snew←xnew的评分和个体差异性
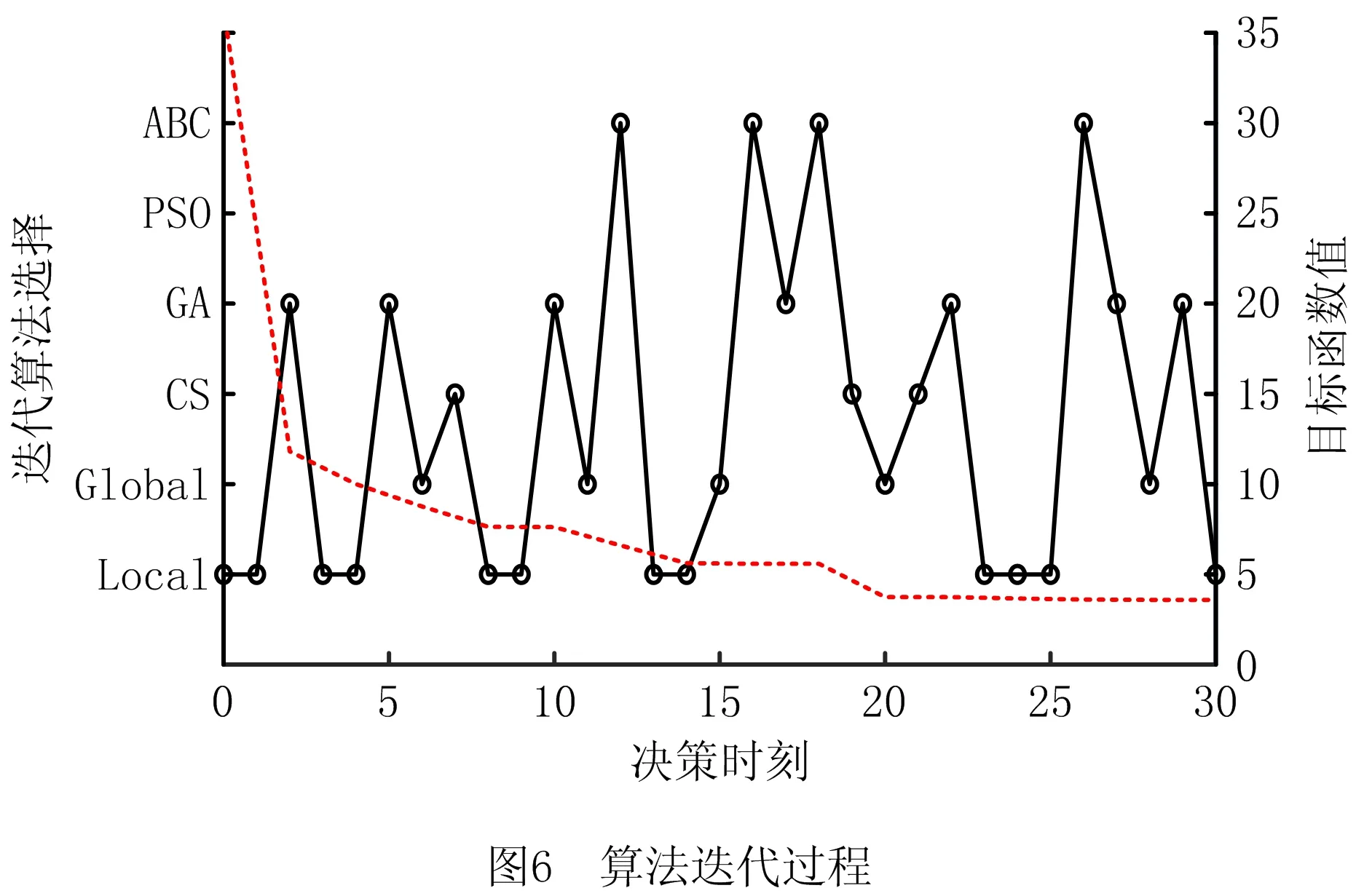
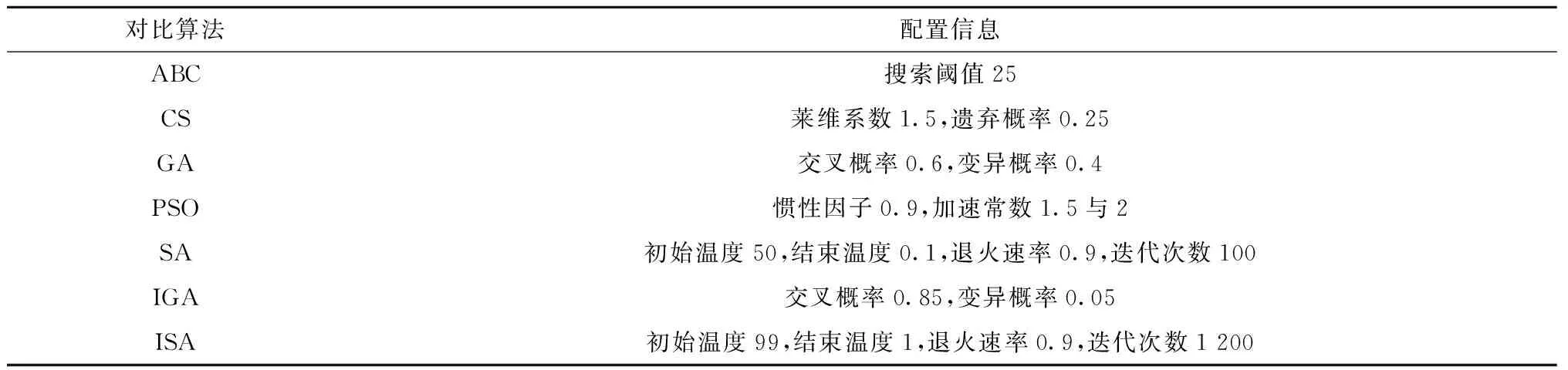
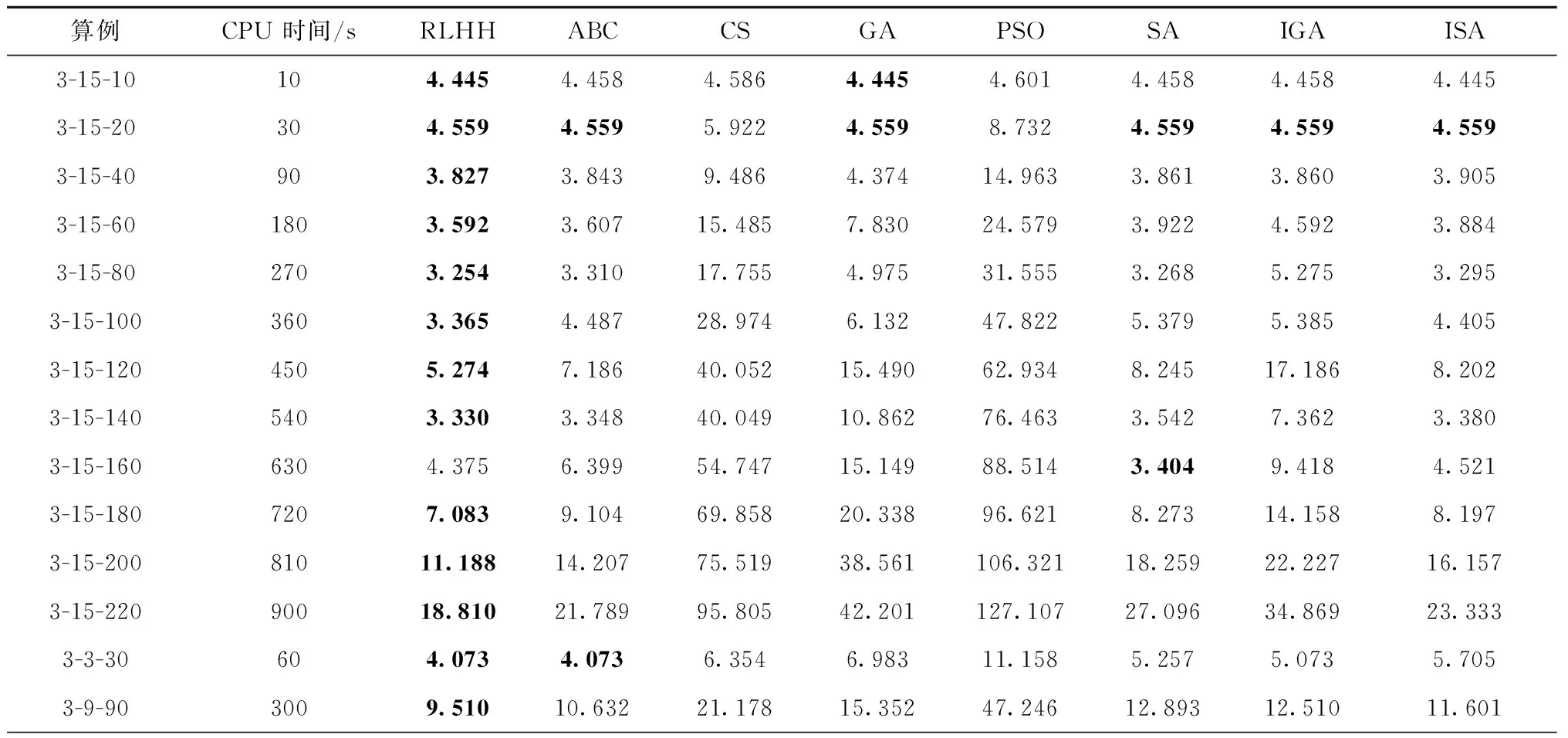
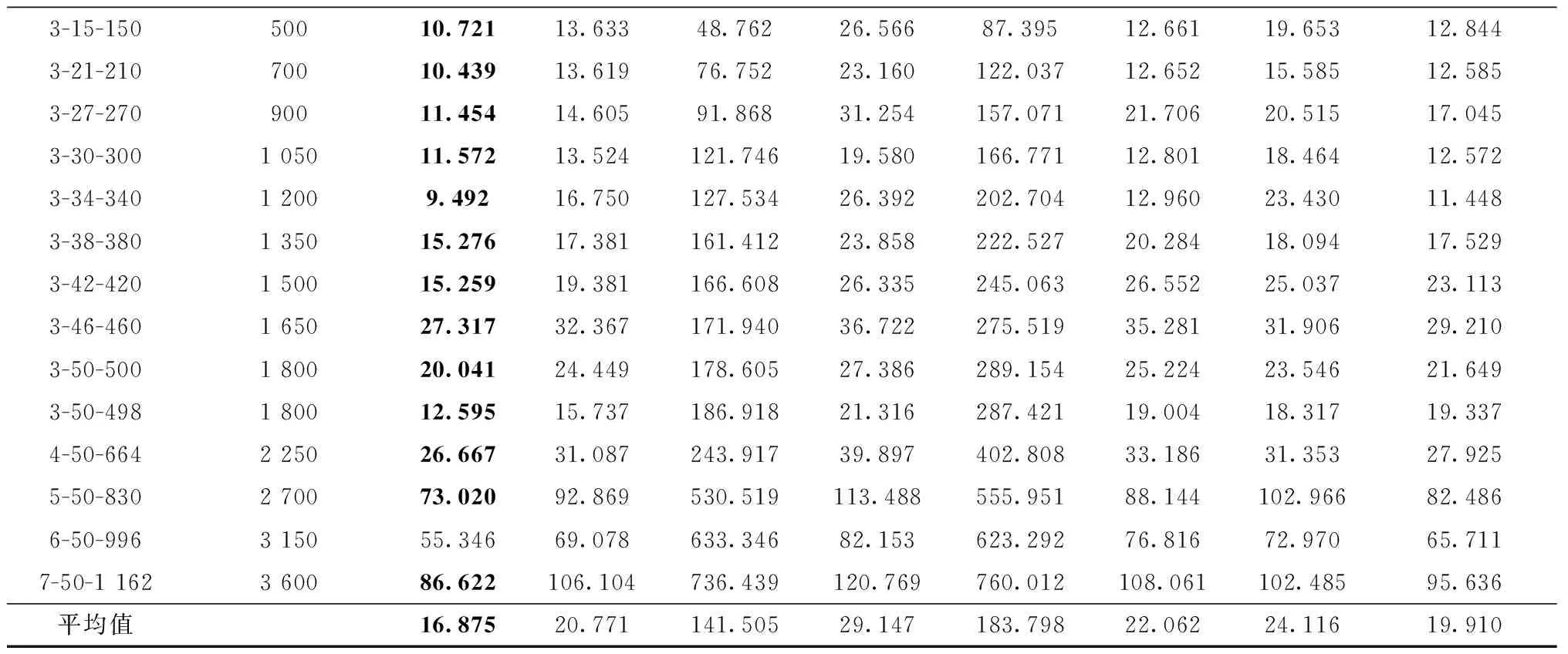
15:ifi 16:r← 0 17:else 18:r← 整个过程中的评分提升 19:returna,snewandr end 3.4.3 回报 回报定义了强化学习策略的目标,并根据状态变化提供了选取动作的即时和后续效果。在此过程中,强化学习算法选择动作以最大化总回报,并尝试在回报的指导下达到最终目标。在本文研究的问题中,总体目标是找出最优的箱位分配方案,最小化任务的不平衡性以及后续的翻箱率。因此,这一评价指标将随着算法迭代而持续下降,直到最终获得较好的分配方案。在算法中,为了更好地表征策略的好坏,回报被定义为最终状态与初始状态之间的评价方案的差值,并在最后给予算法。 3.4.4 训练方式 RLHH算法引入基于策略的演员—评论家框架,以提取状态中的隐藏模式,因此算法是一种在线学习(on-policy)方法。由于传统的演员—评论家框架需要较长时间进行训练,近年来人们引入了A3C方法[31]。A3C方法是一种新颖的强化学习训练方式,可以充分利用多线程来加速训练过程,以满足实际问题的需要。在提出的算法中,系统包括一个中心线程和多个工人线程。中心线程负责更新和训练网络,并为工人线程提供网络参数;工人线程使用来自中心线程的网络参数并且并行运行算法,以收集不同情况下的状态、动作和奖励。这一并行训练过程可以大大加快训练过程,并显著减少运行时间。 在工人线程收集了足够的训练数据之后,算法将对神经网络进行训练,并从所有工人线程的经验即每个决策时刻的状态,行动和奖励中学习。训练过程在中心线程运行,第一步是使用称为事件的线程同步方法挂起所有工人线程。然后,中心线程使用所有收集的数据来训练演员和评论家网络。对于演员网络,算法采用式(22)所示的目标进行更新[18]。 (22) 式中:rt(θ)为新策略与旧策略的比值,可以使用新的策略梯度网络和旧的策略梯度网络进行计算;At为预测的差异,从收集的数据中获得的回报与评论家网络计算出的相应状态的价值之间的差异得到。对于评论家网络,训练过程相对容易。这一网络的损失是上述预测的差异,可以表现状态值的预测性能。最后,在演员和评论家网络都完成训练之后,中心线程使用事件告诉所有工人线程可以使用新的网络参数来继续收集数据。训练过程的伪代码如算法3所示。 算法 3TrainNetwork()。 输入:事件mutex,网络参数a_para,a_paraold,c_para; 输出:事件mutex,更新的网络参数a_para,a_paraold,c_para。 begin 1:mutex← 等待状态 2:a_paraold←a_para 3:tmax←rb的长度 4: 状态的价值vs← critic (sb) 4: forj←1 totmaxdo 5:s←sb[j],a←ab[j],r←rb[j],v←vs[j] 6: 预测差异adv←r-v 7: 新的策略梯度newp← actornew(a) 8: 旧的策略梯度oldp← actorold(a) 9:ratio←newp/oldp 10: 演员网络的损失aloss由式(22)计算得到 11: 训练演员网络并更新a_para 12: 评论家网络的损失closs←adv 13: 训练评论家网络并更新c_para 14:end 15:sb,ab,rb← empty 16:mutex← 就绪状态 17:returnmutex,a_para,a_paraold,c_para end 3.4.5 神经网络结构 在演员—评论家框架中,演员网络在每个决策时刻计算策略梯度,而评论家网络预测状态的价值以教导演员网络从而得到更好的策略梯度。两个网络共享相同的状态输入,即种群的质量与分散程度。但两个网络具备不同的输出,其中演员网络输出计算动作需要的策略梯度,而评论家网络输出状态的价值,用于指导演员网络的迭代。因此,本文采用相似的神经网络结构来搭建演员和评论家网络。输入的状态首先会分为个体分数和个体差异两部分。然后,这两部分分别经过两次卷积层和池化层以提取其中的隐藏信息,定义当前种群的特点。之后,网络将结果合并为完整的数据并通过全连接层将所有信息汇总在一起,形成状态的分类。最后,网络使用归一化技术并输出。 为了验证所提RLHH算法的有效性及其性能,本文基于洋山四期自动化集装箱堆场的实际场景设计了一系列不同规模的问题。所有实验均在TensorFlow 1.4,Python 3.5、16 GB RAM和i7-8 700 CPU的环境下实现。同时,为了让算法的性能达到最优,本文通过实验得到RLHH的超参数,如表2所示。最后,为了更直观地获得所提算法的性能,本文引入不同问题中常用的性能较高的一系列智能算法如遗传算法、模拟退火算法[7,15]等进行算法比较。 表2 超参数选择 本文算例的数据主要根据以下规则产生: (1)问题规模 根据洋山四期自动化集装箱堆场的布局方案,生成对应一个泊位的数个箱区的场景。为了兼顾有限的运算资源,设计了较小规模的实验以更好验证算法性能以及根据堆场轨道吊工作效率以及出口箱任务数量生成大规模的实际箱位分配问题。 (2)箱区现状 根据堆场箱位实际的利用率,初始时刻每个箱区内已存放50%的集装箱,已堆存集装箱的箱位随机产生。 (3)出口箱入场顺序 由于外集卡的到达时间随外围交通、外集卡自身时间安排决定,不存在必须遵守的约束,因此每个出口箱的入场顺序随机产生。 (4)作业顺序 根据船公司提供的船舶预配载图以及预先决定的桥吊作业顺序和船舶积载方案,预先制定海侧轨道吊的作业顺序,即各集装箱的海侧出场作业顺序。 由于本文提出的RLHH算法中采用强化学习方法作为高层策略,需要前期的训练过程以最大化算法性能。在此过程中,本文引入了多线程并行方式以加速训练过程。在训练过程中,本文采用上述方法生成的问题来提供训练算例,并基于问题的复杂程度设置了对应的训练数据集。训练数据集包含了随机生成的900个不同规模的算例,包括300个3个箱区较小倍位数的小规模算例、300个3个箱区较大倍位数的中等规模算例以及300个7个箱区的大规模算例。由于每个算例中均需要强化学习算法进行数十次的算法决策,上述训练数据集能够满足算法的训练要求。在训练过程结束后,使用生成的强化学习模型开展测试以验证其性能。为了直观地体现算法迭代过程,以3个箱区15个倍位的堆场和60个出口箱任务为例,使用所提算法开展研究,算法迭代过程如图6所示。 由此可以得到在迭代过程中,目标函数值不断下降,并且算法能够选择不同的启发式算法来尽可能增加这一下降率。具体来说,在早期,由于种群随机产生,算法倾向于选择局部搜索算子、遗传算法、人工蜂群算法来寻找局部最优值。之后,在找到局部最优值并且最优值不变时,算法改变策略,选择全局搜索算子或具有强大探索能力的布谷鸟算法。由于找到了新的搜索领域,算法重新选择局部搜索能力较强的算法来寻找新的局部最优。算法不断重复该过程,直到输出最终解决方案为止。因此,所提RLHH算法可以在有限的迭代过程内获得较好的结果,也证明了其有效性。 为了进一步研究RLHH算法用于出口箱箱位分配问题的有效性和性能,本文建立了一系列箱位分配问题算例,并引入其他常见的智能算法如人工蜂群算法( Artificial Bee Colony algorithm,ABC)、布谷鸟算法(Cuckoo Search algorithm,CS)、遗传算法(Genetic Algorithm,GA)、粒子群优化算法(Particle Swarm Optimization,PSO)和模拟退火算法(Simulated Anneal algorithm,SA)以及近期研究中采用的改进的遗传算法(Improved GA,IGA)[11]、改进的模拟退火算法(Improved SA,ISA)[15]开展对比试验,从而比较算法性能并验证本文算法使用的必要性和优越性。由于求解问题存在差异性,相关对比算法在近期研究的参数选择基础上均采用了正交实验来获取最佳的参数组合,相关参数如表3所示。为了更完整地得到算法性能对比结果,本文采用控制变量的方法来设计算例。因为问题规模由箱区数量、倍位数量以及出口箱任务数量决定,所以全部算例也相应分为3个部分。整个实验的结果如表4所示。其中对于每个算例,本文控制了每个算法的计算时间,以确保所有算法使用相同的计算能力,并能用于实际问题,参数计算时间表示了实验中算法的最大计算时间。此外,参数中名为“X-Y-Z”的算例表示X个箱区Y个倍位的堆场以及Z个出口箱任务。 表3 对比算法配置 表4 算法对比结果 续表4 根据表4的实验结果,可以得出以下结论。在自动化集装箱码头出口箱箱位分配问题中,本文提出的RLHH算法能够在有限的时间内得到较好的可接受的箱位分配方案。算法能够在全部28个算例中的27个获得最佳的箱位分配方案。而在“3-15-60”算例中,模拟退火算法得到了最佳的箱位分配方案。此外,在全部算例的箱位分配方案的平均结果中,RLHH算法获得了最好的算法评价,较其他常见的智能算法有18.8%以上的提升,较近期研究中改进的智能算法有15.2%的提升。因此可以看出,提出的RLHH算法具备比单一智能算法更好的性能,能够更好地求解研究的出口箱箱位分配问题。 另外,为了更直观比较提出的RLHH算法与智能算法的算法性能,本文通过式(23)计算算法之间的性能差距, (23) 其中X表示当前算法,T(X)表示X算法得到的目标函数的平均值。由于表6中人工蜂群算法在常见智能算法中的表现最好,采用这一算法为性能基准,即以当前算法与人工蜂群算法的性能对比表现算法之间的性能差距。此外,由于目标函数值越小意味着箱位分配方案越合理,INC值越低意味着算法性能越好。根据3组算例得到的算法对比图如图7所示。 从图7的3个部分算法对比中可以看出,所提出的算法的INC值在0%~-27%之间,且在大多数情况下具有最低的INC值。此外,随着问题规模的增加,RLHH算法的INC值存在下降趋势。因此可以得出结论,RLHH算法具有最佳的性能,并且能在较大规模的实际问题中取得更好的效果,具备应用价值。 总之,从上述实验可以得出以下结论。本文提出的RLHH算法能够根据当前迭代情况智能选取合适的启发式算法进行接下来的迭代,从而得到更好的箱位分配方案。同时,针对研究的箱位分配问题,提出的算法能够获得比常见的智能算法更好的箱位分配方案,在不同情况下的性能提高了15%。并且在较大规模的实际问题中,所提算法具备更好的效果,提供具备使用价值的高性能计划方案。 在自动化集装箱码头的出口箱箱位分配问题中,由于具有问题规模极大、动态性强、场桥接力、多箱区协同等特性,现有研究存在较大的提升空间。为了更好地解决这一问题,本文基于滚动计划的方法,构建了一个以最小化任务不均衡性和翻箱率为目标的出口箱箱位分配问题模型。在堆场初始堆存状态、出口箱入场和出场顺序已知的情况下,提出了一种基于强化学习的超启发式算法得到箱位分配方案。该方案将强化学习和深度学习用作高级选择策略,将启发式算子、智能算法用作低级启发式方法。经过不同规模的实验,并与常规及近期研究采用的智能算法进行对比,证明了本文所提算法能够有效解决这一箱位分配问题,并且在算法表现上优于不同的智能算法,从而表明所提算法能够提供高水平的箱位分配问题解决方案。 尽管本文研究解决了这一具有挑战性的出口箱箱位分配问题,但将来可以尝试更多的工作来进一步改善算法,以实现更高的效率和性能。第一个改进方向是在强化学习策略中开发更有效的网络结构和框架;另一个方向是引入更多更有效的低级启发式算法,包括但不限于智能算法、启发式算子和混合算法;最后,可以考虑更复杂的堆场场景和问题,从而使所提算法能够启时更多的挑战。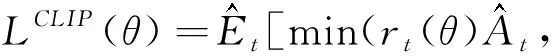
4 实例验证

4.1 算例生成
4.2 算法结果分析
4.3 算法比较分析
5 结束语
