含齿根裂纹风电行星齿轮传动系统动态特性研究
2022-09-05谢福起巫世晶李小勇王晓笋
谢福起,巫世晶,李小勇,王晓笋
(武汉大学 动力与机械学院,湖北 武汉 430072)
0 引言
齿轮箱是风电机组核心部件之一,在低速、重载、复杂多变的工况下运行时,其齿轮容易发生齿面点蚀、齿根裂纹等失效问题,从而导致齿轮传动系统可靠性逐渐降低,甚至造成风电齿轮箱故障。因此,研究故障与征兆之间的联系,对风电齿轮箱状态评估和故障诊断有重要意义。
WAN等[1]考虑齿根圆和基圆不重合问题,对势能法计算啮合刚度进行改进,研究了齿根裂纹对定轴齿轮传动系统动态响应的影响;MOHAMMED等[2]建立含故障的齿轮啮合刚度计算模型,研究了含裂纹故障齿轮传动系统振动特性[2],对含故障齿轮建模和动力学分析的相关研究进行了总结[3];孟宗等[4]研究了裂纹深度对时变啮合刚度和定轴齿轮传动系统振动响应的影响;MA等[5-6]改进含裂纹直齿轮时变啮合刚度计算模型,总结归纳了含裂纹齿轮传动系统动力学的研究进展;DOAN等[7]用有限元法计算含裂纹齿轮时变啮合刚度,研究了裂纹对齿轮系统动态传递误差的影响;刘杰等[8]计算太阳轮单齿裂纹故障对齿轮副时变啮合刚度和系统动态响应的影响,揭示了行星齿轮传动系统裂纹故障机理;桂勇等[9]计算含裂纹齿轮副的时变啮合刚度,分析了太阳轮、行星轮、内齿圈分别发生单齿裂纹时,系统响应的包络谱结构和频谱特征;CHEN等[10]研究了考虑齿圈柔性和单齿根裂纹时系统的动态响应和频谱特征;LIANG等[11]研究了裂纹对行星齿轮传动系统时变啮合刚度的影响;王一凡等[12]通过试验研究了行星轮系不同部件单一故障下系统的时域特征和频谱特征;LIU等[13]研究了时变输入转矩作用下太阳轮含单齿裂纹时系统的动态响应和阶次谱特征;JIANG等[14]考虑振动信号时变柔性传递路径,基于行星齿轮系动力学模型揭示了裂纹故障机理;HAN等[15]计算了含裂纹齿轮副的时变啮合刚度,考虑行星轮的通过效应,研究了含裂纹故障行星轮系的特征;CHEN等[16]研究了轴承间隙和齿根裂纹对行星齿轮系统振动响应的影响;舒斌等[17]和张振等[18]研究了多齿裂纹对时变啮合刚度的影响。上述研究主要集中在恒定输入转速、转矩下含单齿根裂纹的齿轮传动系统,而对时变输入转速、转矩和双齿根裂纹工况的研究较少。
本文以风电行星齿轮传动系统为对象,利用风速功率谱密度模型描述时变风速,结合风力机运行特性,计算系统时变输入转速和转矩,综合考虑时变啮合刚度、啮合阻尼、轴承支撑刚度和阻尼、齿侧间隙、综合误差等内激励,采用集中参数法建立考虑行星架旋转的系统平移-扭转耦合非线性动力学模型,并通过仿真对比分析了定载荷、变风载作用下同侧双齿沿齿厚贯穿型齿根裂纹对系统动态特性的影响,探究了双齿根裂纹与系统征兆之间的联系,为裂纹诊断与定位提供了理论基础。
1 系统动力学模型
某半直驱风电机组采用NGW式行星齿轮传动系统,建立内齿圈r固定、行星架c输入、太阳轮s输出、3个行星轮pi(i=1,2,3)的行星齿轮传动系统动力学模型,如图1所示。
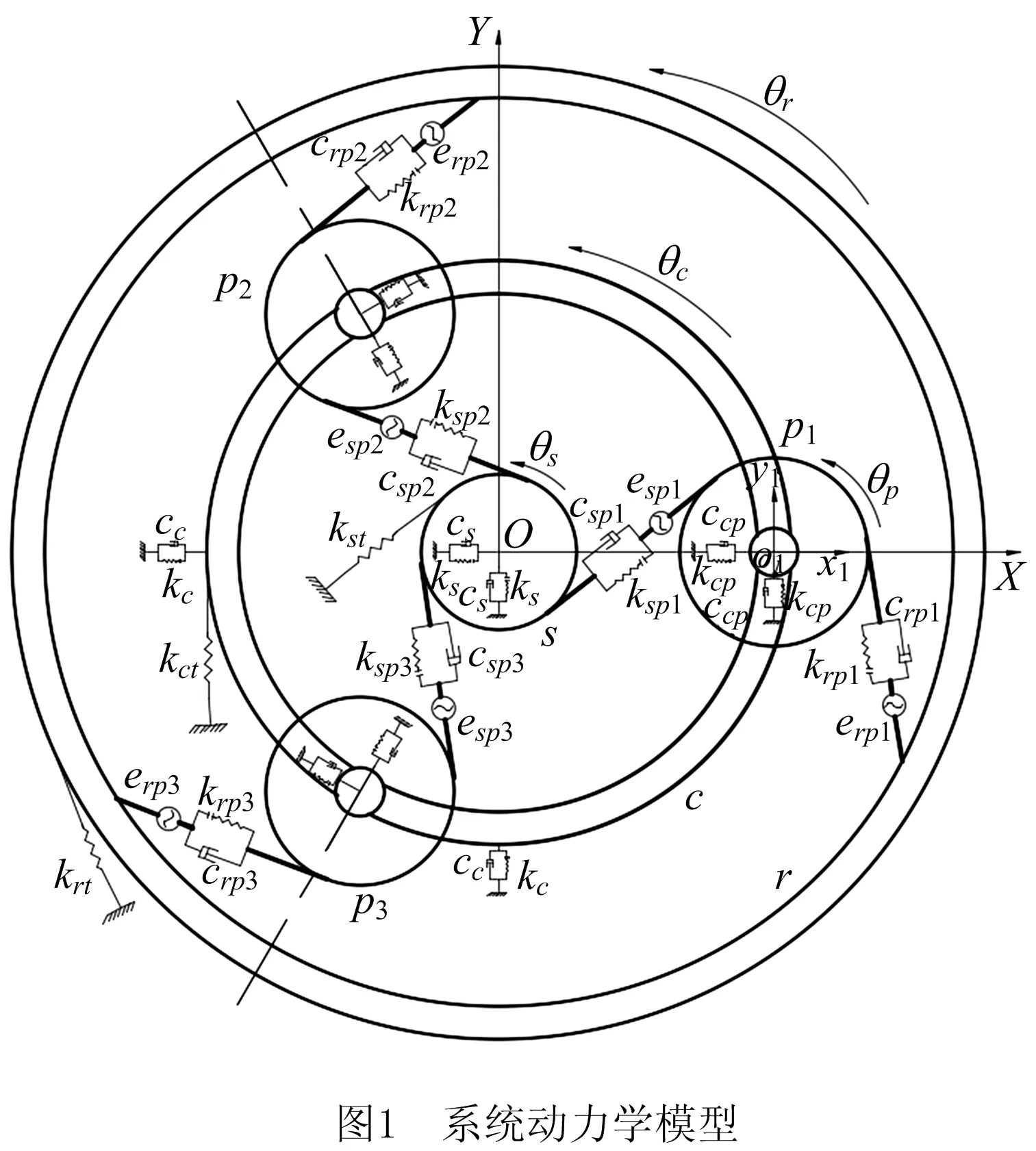
图1中:kn、knt(n=c,s,r,cp)分别为各构件的平移支撑刚度和扭转刚度;kj、cj、ej(j=spi,rpi)分别为各齿轮副的啮合刚度、啮合阻尼和综合误差。
1.1 综合误差和齿侧间隙
齿轮在制造、安装过程中,不可避免地会产生齿廓偏差、偏心误差和径向圆跳动等,这些误差均会对系统振动产生激励。可将综合误差表述为[19]:
ej(t)=E0j+Ejsin(ωmt+φj)。
(1)

由于润滑的需要,以及轮齿在长时间使用过程中的磨损,啮合轮齿对之间会存在齿侧间隙。通常使用分段函数来描述轮齿形变[20]:
(2)
式中:b为单侧齿侧间隙,δj为相对啮合位移。
1.2 系统动力学微分方程
假定图1中标明的逆时针方向为各构件运动方向,构件振动使啮合线处于压缩状态时,符号为正。各构件之间的相对位移如下:
太阳轮-行星轮沿啮合线相对位移:
(3)
行星轮-内齿圈沿啮合线相对位移:
(4)
行星轮-行星架沿x、y方向相对位移:
(5)
其中:xii、yii、uii(ii=s,c,r,pi)分别为构件ii的平移线位移和扭转位移;φspi=ψpi-α、φrpi=ψpi+α分别为太阳轮-行星轮pi、内齿圈-行星轮pi的啮合角;ψpi为行星轮pi在坐标系中的相对位置角;α为压力角。取各构件的平移和扭转共18个自由度为系统的广义坐标,系统的动势L如式(6)所示。
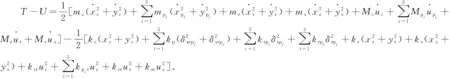
(6)
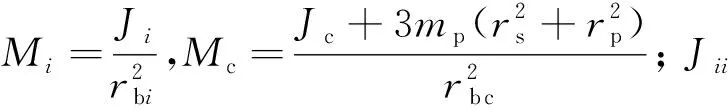
由第二类Lagrange方程得行星轮系非线性动力学微分方程组如式(7)~式(10)所示。
太阳轮s非线性运动微分方程:

(7)
行星架c非线性运动微分方程:
(8)
行星轮pi非线性运动微分方程:
(9)
内齿圈r非线性运动微分方程:
(10)
2 含裂纹齿轮副时变啮合刚度计算
本文采用改进势能法计算时变啮合刚度[1],考虑了齿根圆和基圆尺寸不一致的情况,计算齿轮副啮合时的赫兹接触刚度kh、弯曲刚度kb、剪切刚度ka、径向压缩刚度ks和轮齿基体柔性刚度kf,单齿啮合时的啮合刚度可表示为:
(11)
含齿根裂纹的齿轮示意图如图2所示。图中:q为裂纹深度,γ为裂纹方向与轮齿中心线夹角,rf、rb分别为齿根圆和基圆半径,2hr为齿顶高,hx为x处到轮齿中线的距离,hd为渐开线与基圆交点到轮齿中心线距离,hc为裂纹等效点到轮齿中心线距离。
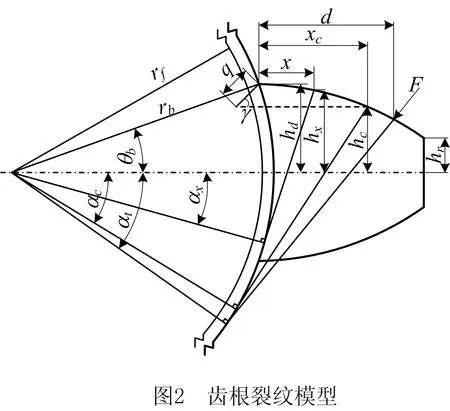
本文考虑的轮齿裂纹,宽度很小,裂纹处材料并未减少,可忽略裂纹对赫兹接触刚度、径向压缩刚度和轮齿基体柔性刚度的影响,主要考虑对弯曲刚度和剪切刚度的影响[4]。在实际工程中,裂纹超过齿根圆处厚度一半,轮齿将会快速断裂,因此主要研究hx小于hd的情况。裂纹的存在会导致距离齿根x处的有效惯性矩Ix和截面积Ax发生变化,其计算如式(12)和图3所示。
(12)

图3中:Ix1和Ix2分别为含故障和正常轮齿的有效惯性矩,Ax1和Ax2分别为含故障和正常轮齿的截面积,其计算如式(12)所示,式中B为轮齿宽度。
本文研究的风电行星齿轮传动系统主要参数如表1所示。风电行星齿轮传动系统中,太阳轮出现故障的概率较高[8],本文以太阳轮裂纹故障为例研究。工况如表2所示,其中裂纹角度均为45°[4],均为沿齿厚贯穿型裂纹,q2~q6为单齿裂纹,q7~q9为双齿裂纹齿,且双齿裂纹为两个齿同侧的同参数裂纹。

表1 风机行星齿轮箱主要参数

表2 计算工况
2.1 单齿裂纹
以太阳轮裂纹齿进入啮合为起始,计算工况q1~q6的啮合刚度如图4所示。可以看出,轮齿存在裂纹时,齿轮副时变啮合刚度减小;裂纹齿进入啮合时,啮合点距离齿根部分较远,啮合刚度明显下降,随着啮合不断进行,啮合点逐渐靠近齿根,裂纹对啮合刚度的影响减小。裂纹深度变大,啮合刚度下降幅值变大。
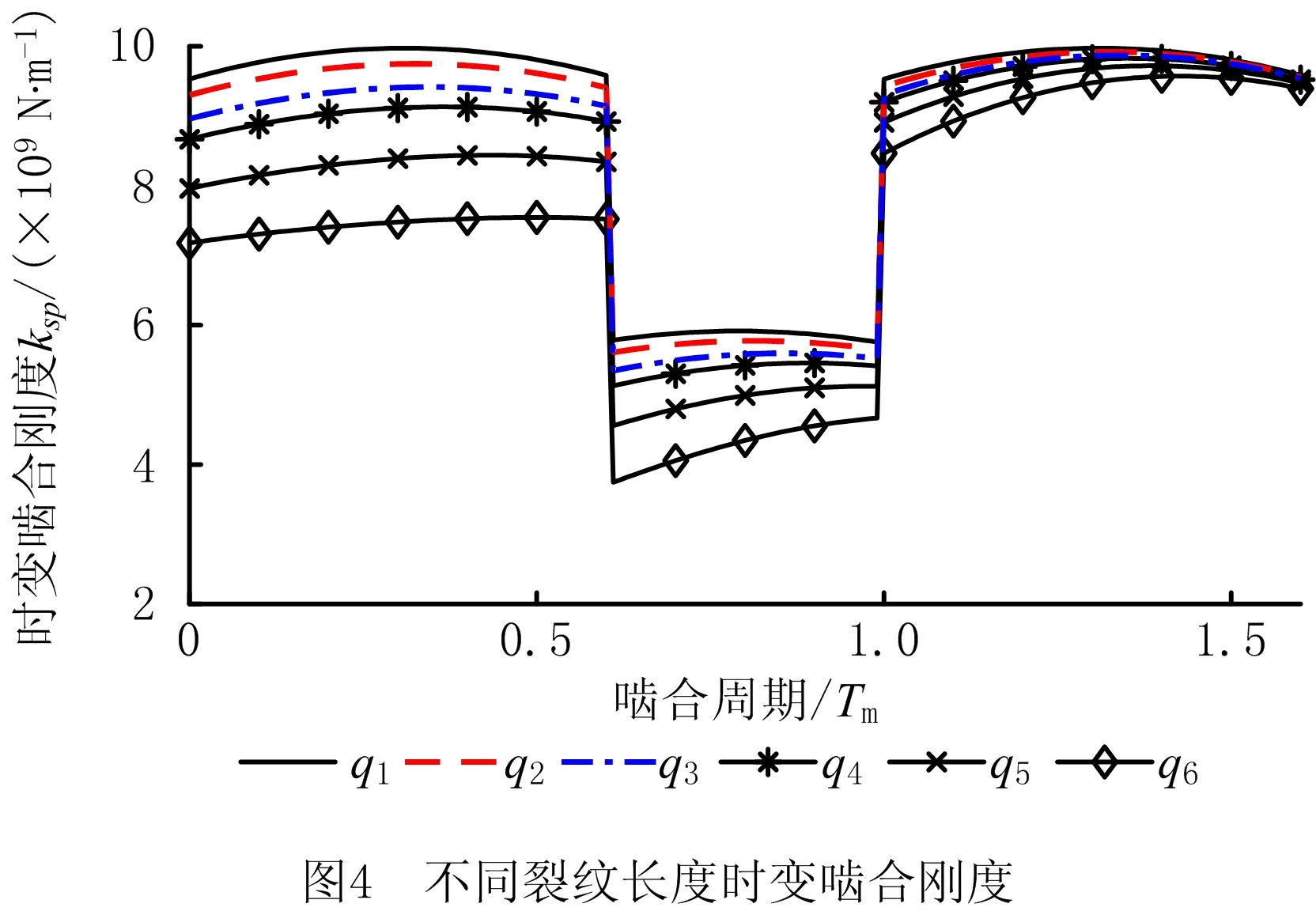
2.2 双齿裂纹
计算工况q7~q9的时变啮合刚度如图5所示。
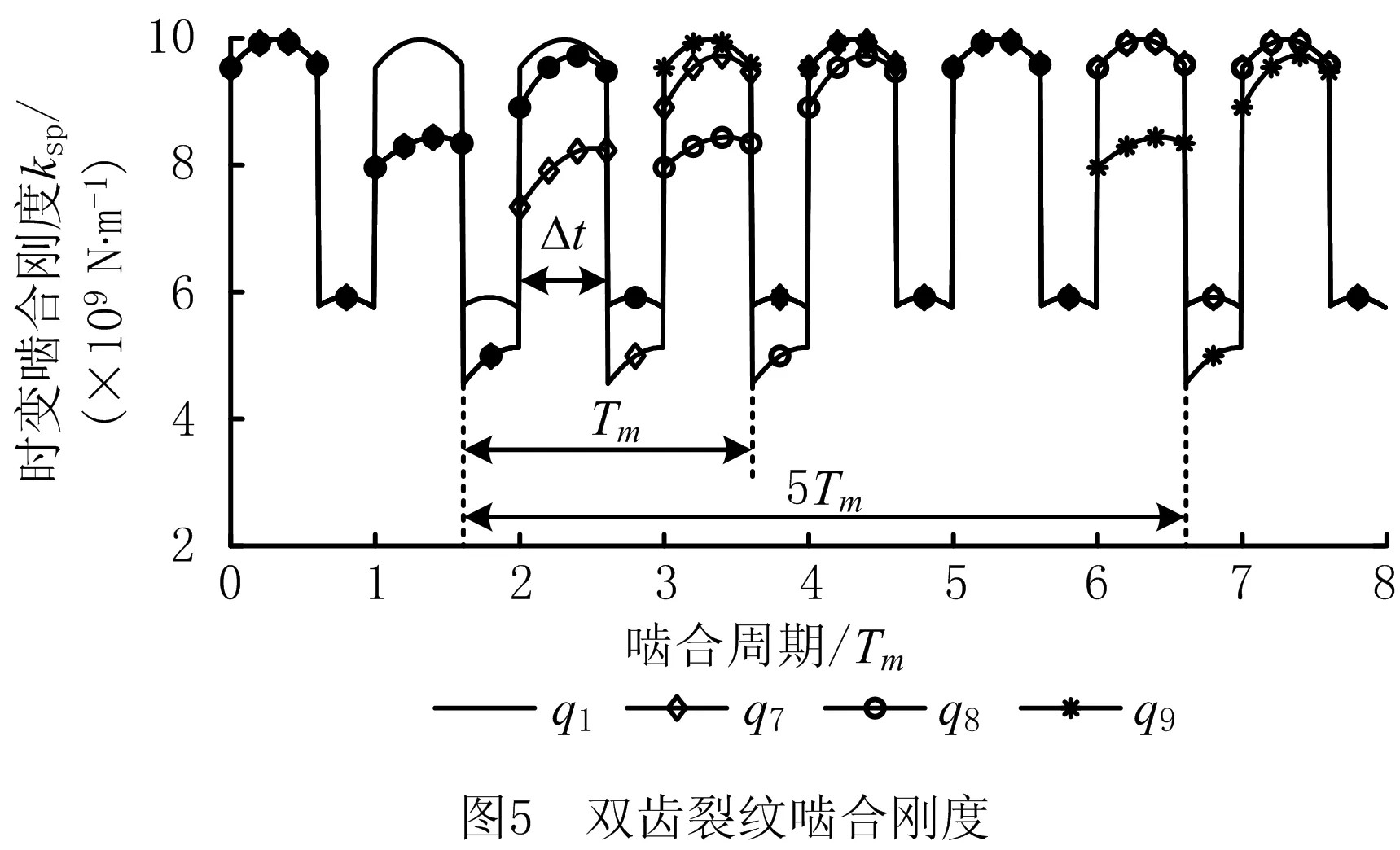
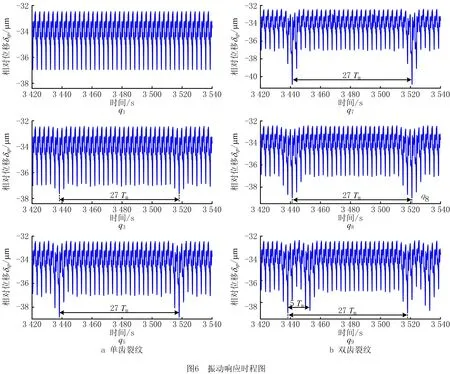
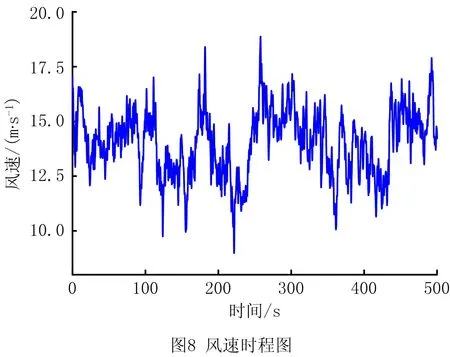
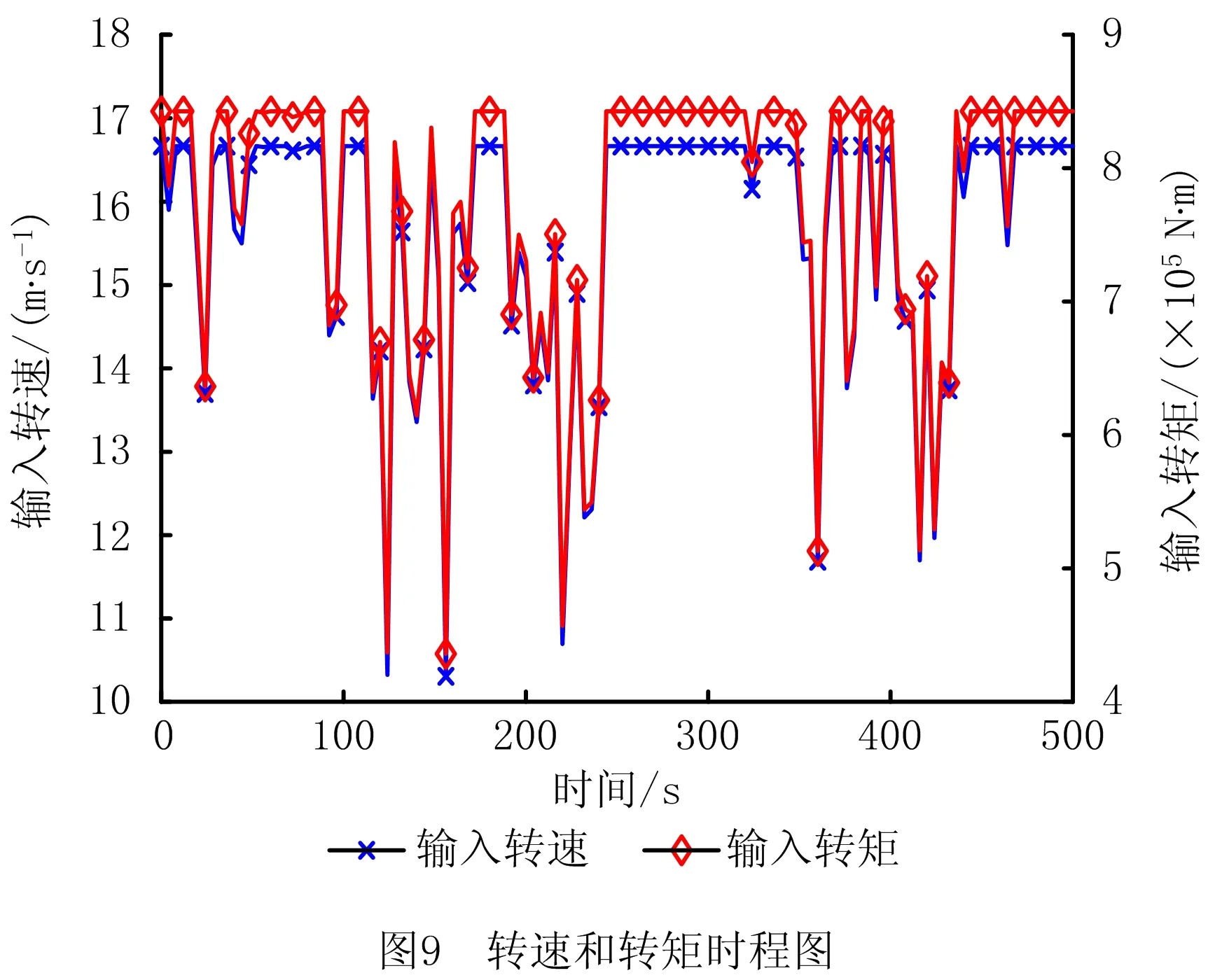
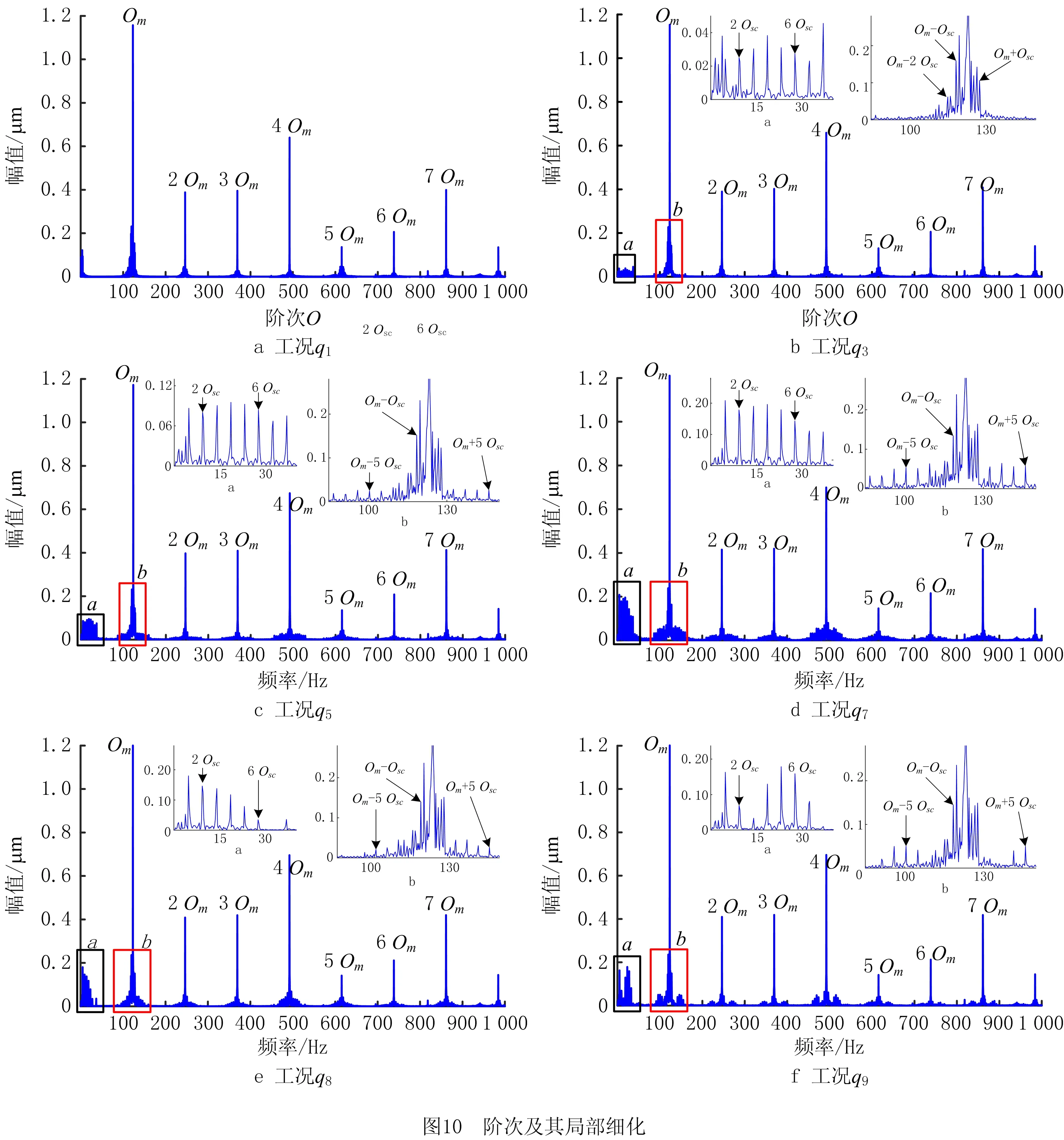
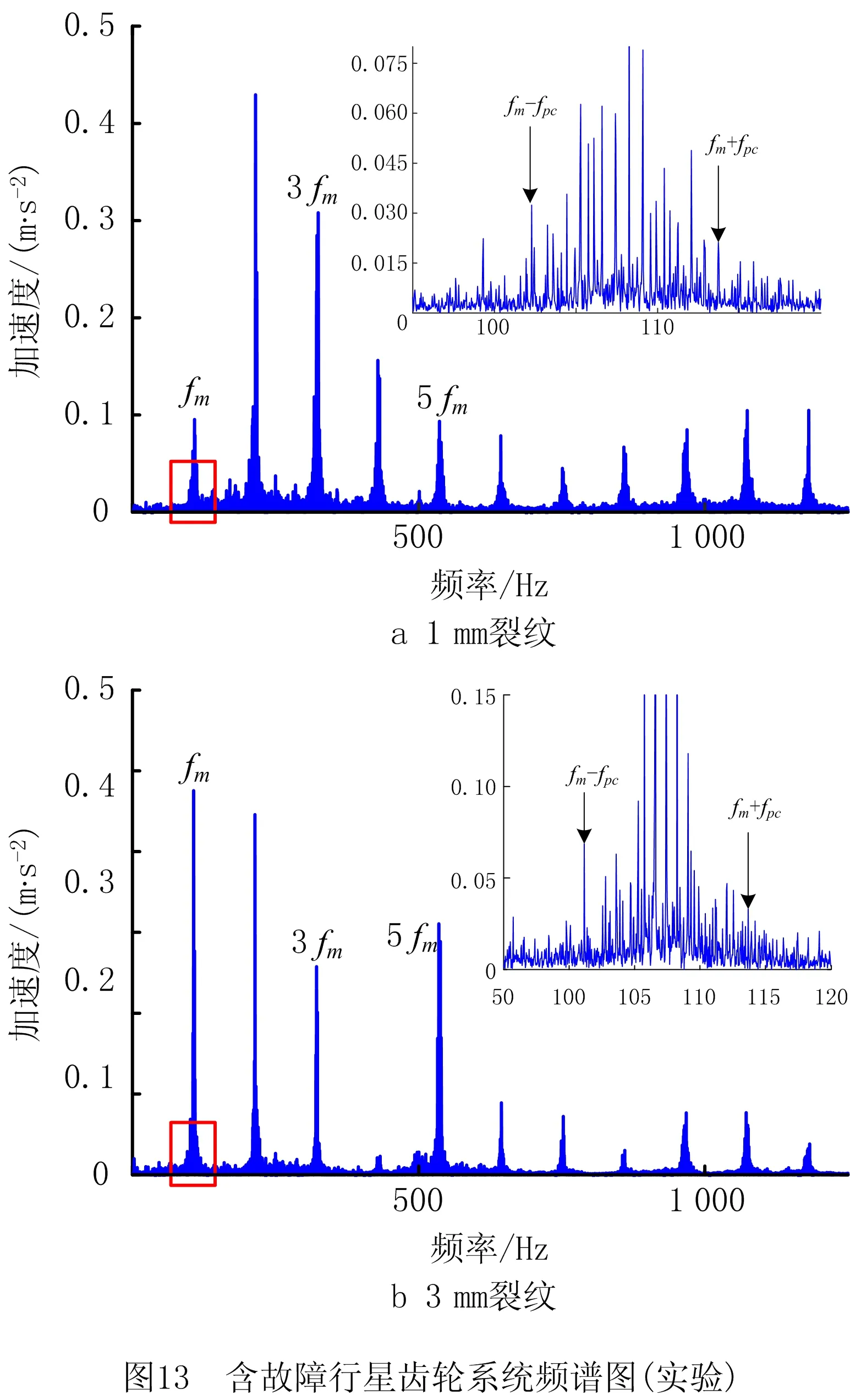
从图5可看出,同一裂纹深度和角度下,两裂纹齿相邻时,裂纹在2.5个啮合周期内对时变啮合刚度均有影响,且在Δt内有较大跌落,这是因为两个裂纹齿同时参与啮合;两裂纹齿不相邻时,齿轮副的时变啮合刚度减少值与单齿裂纹时一致,且在27Tm内,不相邻双齿裂纹会出现2次刚度减小,间隔时间为nTm(n为裂纹齿间间隔的正常齿个数,0 根据表1中风电行星齿轮系统的主要参数,计算系统特征参数如表3所示,表中fm、Om分别为啮合频率和啮合阶次[25],且行星架对应阶次为1,fsc、Osc分别为太阳轮局部故障频率1/3倍和太阳轮局部故障阶次1/3倍。采用龙格库塔法计算系统动态响应,齿轮误差激励参数按GB/T 10095—2008选取,太阳轮和行星轮为5级精度,内齿圈为6级精度。行星齿轮系统振动信号的激励主要为太阳轮-行星轮啮合副和行星轮-内齿圈啮合副的啮合力[21],为探究裂纹对系统振动的影响规律,计算并分析太阳轮—行星轮p1振动位移响应。 表3 行星齿轮传动系统特征参数 计算定转速下工况q1、q3、q5、q7~q9的太阳轮—行星轮p1的振动位移响应如图6所示。 由图6可以看出,系统振动位移响应具有明显的周期性,当裂纹齿参与啮合时,啮合刚度下降,系统出现冲击现象。单齿裂纹时,相邻冲击之间间隔为27Tm,这是因为太阳轮旋转一周,太阳轮的裂纹齿与行星轮p1啮合一次;随着裂纹深度变大,啮合刚度不断减小,冲击幅值越大。双齿裂纹时,工况q7的齿轮副啮合刚度明显下降,冲击幅值明显增大,相邻冲击间间隔为27Tm;工况q8下,冲击时间变长,冲击幅值与工况q5下的一致,相邻冲击间间隔为27Tm;工况q9下,太阳轮旋转一周,系统产生了两次冲击,间隔为5Tm,冲击幅值均与工况q5下的一致,第一次冲击和第三次冲击间间隔为27Tm。 为进一步分析裂纹对系统动态特性的影响,对图6中各工况的振动响应进行频谱分析,并将啮合频率附近和低频部分进行细化,如图7所示。 从图7可以看出,正常状态下,系统的频率成分主要为啮合频率fm及其2~7倍频;当太阳轮存在裂纹时,频谱图中出现低频成分,啮合频率及其倍频附近存在边频带,谱线间隔约为1.25 Hz,与fsc相等。太阳轮单齿裂纹时,裂纹深度变大,低频成分和边频带的幅值变大。工况q7,在同一周期内存在两裂纹齿同时参与啮合的时段,啮合刚度下降幅度较大,边频带和低频成分的幅值明显变大;将工况q8与q9和q5对比,两裂纹齿进入啮合的时刻不同,边频带和低频成分的幅值有明显变化:工况q8,低频成分中频率为nfsc(n= 1,2)和边频带中频率为fm±nfsc(n= 1,2,3)的幅值变大,低频成分中频率为nfsc(n= 7,8)和边频带中频率为fm±nfsc(n= 7,8)的幅值变小;工况q9,低频成分中频率为nfsc(n= 1,5,6)和边频带中频率为fm±nfsc(n= 1,5,6)的幅值变大,低频成分中频率为nfsc(n=3,8)和边频带中频率为fm±nfsc(n= 3,8)的幅值变小。 风电齿轮箱所受激励为自然风,具有时变性。目前,模拟风速的方法有很多,如威布尔分布模型、瑞利分布模型和自回归线性滤波模型等。本文采用风速功率谱密度模型[22]描述自然风Vw(t),该模型考虑平均风速Vm和湍流部分Vr(t),与风电场实际情况更吻合,模型可表示为: Vw(t)=Vm+Vr(t)。 (13) 某风场的平均风速为12 m/s,本文研究的半直驱风电机组的设计参数为风机叶轮直径为90 m。计算500 s风速时程曲线如图8所示。 根据风力机运行特性[23]:当风速小于风机切入风速或大于切出风速时,风机停止运行,输入转速和转矩为0;风速大于切入风速小于额定风速时,齿轮传动系统的输入转矩和转速可表示为: (14) 式中:Tr为额定转矩;vr为额定风速;ωr为额定转速。 计算得到风轮输入转速和输入转矩如图9所示。 将计算得到的输入转速和输入转矩进行多阶傅里叶拟合,引入所建立的动力学微分方程。阶次分析作为一种分析变转速旋转机械部件故障的重要方法[25],适用于工况q1、q3、q5、q7~q9的太阳轮—行星轮p1的振动位移响应的分析,结果如图10所示。 从图10可以看出,正常状态下,振动位移响应的峰值阶次主要为啮合阶次Om及其2~7倍谐次。当太阳轮存在齿根裂纹时,啮合阶次及其谐次无明显变化;受太阳轮局部故障阶次调制,啮合阶次的边带阶次中出现Om±nOsc(n= 1,3…8),低阶成分出现nOsc(n= 1,3…8)。太阳轮单齿裂纹时,裂纹深度增加,低阶成分中Osc及其谐次、啮合阶次的边带阶次Om±nOsc(n= 1,3…8)的幅值变大,其中裂纹深度为6 mm时,啮合刚度小幅下降,故障引起的冲击较小,与故障相关的阶次幅值也较小。工况q7,低阶成分中Osc及其谐次、啮合阶次的边带阶次Om±nOsc(n= 1,3…8)的幅值明显变大,这是因为在同一周期内存在两裂纹齿同时参与啮合的时段,啮合刚度下降较明显,故障导致的冲击较大。将工况q8和q9与q5对比,两裂纹齿进入啮合时刻不同,边带阶次和低阶成分的幅值有所区别:工况q8,低阶成分中nOsc(n= 1,2,3)、啮合阶次的边带阶次Om±nOsc(n= 1,2,3)的幅值变大,低阶成分中nOsc(n= 6,7,8)、啮合阶次的边带阶次Om±Osc(n= 6,7,8)的幅值变小;工况q9,低阶成分中nOsc(n= 1,4,5,6)、啮合阶次的边带阶次Om±nOsc(n= 1,4,5,6)幅值变大,低阶成分中nOsc(n= 3,8)、啮合阶次的边带阶次Om+nOsc(n= 3,±8)幅值变小。 本文在图11所示的装置上开展实验。所试齿轮箱为2K-H行星齿轮箱,输入端为行星架,输出端为太阳轮。采用B&K数据采集仪和4 534-B-001型加速度传感器采集系统振动信息,共布置7个测点。 因实验条件有限,更换太阳轮成本较高,故采用更换行星轮的方式,模拟行星轮1 mm裂纹和3 mm裂纹故障(均为沿齿厚贯穿型齿根裂纹),以验证动力学模型的正确性,如图12所示。 设置工况为:输入转速50 r/min,负载转矩100 N·m,采集点7的信号频谱图如图13所示,系统啮合频率和局部故障特征频率如表4所示。 根据实验工况,利用所建立的动力学模型仿真分析行星轮分别含1 mm裂纹和3 mm裂纹时的系统响应,得到频谱图如图14所示。 从图13和图14可看出,系统主要频率成分为啮合频率及其2~5倍频;裂纹的存在会导致系统振动加剧,频率成分相互调制,啮合频率及其倍频处出现边频带,频率为fm±nfpc(n=±2),且随着裂纹变深,与故障频率相关的边频带的幅值变大。理论仿真和实验分析的系统域分布规律基本一致,验证了该动力学模型的正确性。 风电齿轮传动系统长期在复杂交变载荷作用下运行,不可避免地会出现齿轮裂纹故障,针对此问题,本文结合风电装备变速变载的工作特点,建立了风电齿轮传动系统非线性动力学模型,探究了双齿根裂纹对系统动态特性的影响规律,并通过实验验证了模型和结果的正确性,得到如下结论: (1)齿根裂纹的存在会导致时变啮合刚度局部下降,且裂纹深度增加,刚度下降幅度变大;相邻两齿存在裂纹时,刚度下降幅度比单齿裂纹大。 (2)太阳轮存在齿根裂纹时,阶次谱图中会出现低阶成分,啮合阶次及其谐次附近出现间隔为Osc的边带阶次;裂纹深度增加,低阶和边带阶次幅值变大; (3)相邻两齿存在裂纹时,低阶和边带阶次幅值明显变大;两裂纹齿间间隔n(1 后续针对风电齿轮传动系统动态特性的研究,可加入双馈感应电机的数学描述,建立风电传动系统机电耦合动力学模型。进一步研究、对比不同齿轮出现故障时系统的动态特性,同时考虑振动传递路径的影响,深入分析含故障齿轮传动系统振动信号的调幅-调频机理,提取故障特征,为风电齿轮传动系统的在线监测与故障诊断提供理论依据。3 动力学特性计算与分析

3.1 定载荷激励

3.2 变风载激励
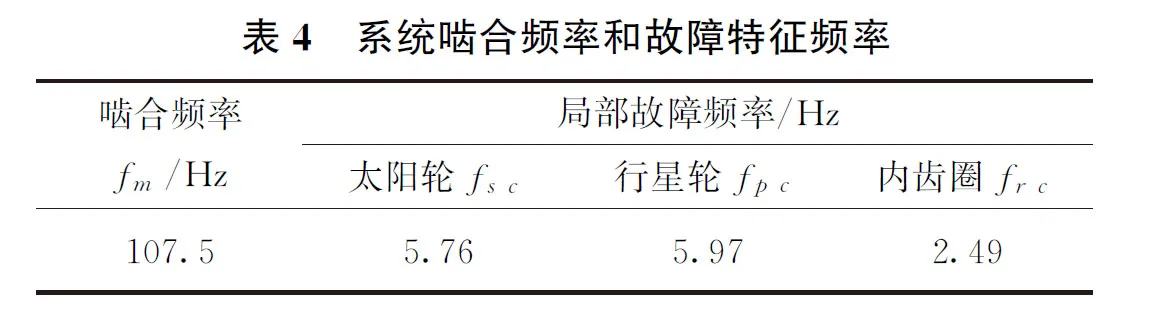
4 实验验证



5 结束语
