设置货箱缓存区的自动小车存储及取货系统订单分批拣选问题
2022-09-05李珍萍韩倩倩仪明超
李珍萍,韩倩倩,仪明超
(北京物资学院 信息学院,北京 101149)
0 引言
随着电商企业的发展,越来越多的电商企业推出了当日达或次日达的配送服务。同时,伴随电商主播的带货热潮,电商企业每天要处理的订单数量激增,如何对这些多品种、小批量的订单进行快速拣选,提高拣选作业效率、降低拣选成本,是电商企业关注的主要问题之一。
传统仓库中采取“人到货”拣选模式,拣选人员行走距离长,造成订单拣选时间较长、人力劳动成本较大的问题。为减少订单拣选时间,企业通常会采用以下两种方式来提高拣选作业效率[1]:①改变拣选策略,如采取分批拣选[2]或分区拣选策略[3];②配置“货到人”拣选系统[4],如自动小车存储及取货系统(Autonomous Vehicle Storage and Retrieval System,AVS/RS)、基于自动引导小车(Automated Guided Vehicle,AGV)的“货到人”系统、基于垂直升降机模块的自动化立体仓库等。
订单分批策略是指将系统中到达的待拣选订单(订单池中的订单)按照某种规则划分成若干个批次,将同一批次订单中的相同品项汇总后进行一批拣选[5]。传统的“人到货”系统订单分批拣选问题的研究成果已经十分丰富[6-9],针对近年来发展起来的“货到人”系统的研究尚在起步阶段[10-16],大部分研究成果集中在储位优化[17-19]与系统设计[20-21]方面,很少涉及订单分批问题。
李珍萍等[11]针对基于AGV的“货到人”系统中订单分批问题,建立了以订单分批拣选总成本最小化为目标的整数规划模型,并设计了K-max聚类算法进行求解;XIANG等[12]针对Kiva公司研发的货到人系统中的订单分批拣选问题进行研究,以搬运货架的总次数最小为目标构建了整数规划模型,利用订单关联度设计启发式算法求解;BOYSEN等[13]针对基于AGV的“货到人”系统中的特定批次的订单排序问题,以搬运货架总次数最小为目标构建了混合整数规划模型,利用启发式算法与动态规划算法进行求解;ELSAYED等[14]研究了自动存储及取货系统的订单分批问题,以最小化订单总完成时间为目标设计了多种启发式算法;FÜßLER等[15]研究了自动存储及取货系统订单分批后的批次内部订单排序问题,以最小化拣选员拣选次数为目标建立了混合整数规划模型,并设计了两阶段启发式算法进行求解;NICOLAS等[16]考虑了配置升降模块的自动存储及取货系统中的订单分批拣选问题,以订单拣选结束时间最早为目标建立了整数规划模型,并利用商业求解器CPLEX进行求解。
以上研究均以提高拣选工作效率或降低拣选成本为目标建立混合整数规划模型,由于订单分批拣选问题往往包含聚类问题、集合覆盖问题等多个NP-hard子问题,因此订单分批拣选问题属于NP-hard问题,现有文献均对问题进行了必要的简化并通过设计启发式算法进行求解。以上文献都没考虑订单中的商品订购数量和每个货箱中存放的商品数量,假设一个货箱中任意一种商品的存储量均可满足一个(或一批)订单对该商品的需求量,且大多文献中都假设一个货箱只存储一种商品,一种商品只存储在一个货箱中。在实际仓库中,为减少货箱出库次数,企业会将经常出现在同一个订单中的多种商品存储在同一个货箱中,为了同时满足多个拣选台对同一种商品的需求,一种商品可能被存储在多个货箱(储位)中。当一个货箱(储位)中存储的某种商品数量小于一批订单对该商品的总需求量时,需要从多个货箱中拣取商品才能满足该批次订单的总需求,李珍萍等[22]针对该场景下的订单分批拣选问题进行了初步研究,假设每个货箱每次出库只能用于一个批次的订单拣选,且服务完该批次订单立刻回库。在这一假设下,以货箱总出库次数最少为目标建立数学模型,并设计了求解模型的算法。因为每个货箱中包含的商品数量和商品种类有限,拣选每批次的所有订单需要使用的货箱较多,所以可能出现拣选不同批次的订单需要出库同一个货箱的情况。因此,在实际订单拣选中,AVS/RS系统中通常会设置容量有限的货箱缓存区,用于暂时存放那些需要在多个批次订单拣选中重复使用的货箱。如果将使用频率较高的货箱暂存在货箱缓存区,用于多个不同批次订单的拣选,则可以减少货箱出库次数,缩短订单拣选时间。
目前,对设置货箱缓存区的“货到人”系统订单分批问题研究较少。JIANG等[23]研究了“人到货”系统中带有缓存区的订单分批及批次排序问题,以最小化总拣选时间为目标建立订单分批拣选模型;吴颖颖等[24]研究设置货箱缓存区的“货到人”系统中的订单排序问题,将订单耦合因子作为参数,建立订单排序优化模型;田彬等[25]研究了设置货箱缓存区的“四向车”拣选系统中的批量订单排序问题,建立了基于改进耦合度的订单排序模型;夏德龙等[26]针对设置货架缓存区的“货到人”系统订单排序问题,提出了以最大化减少货架搬运次数为目标的订单排序模型。由于“人到货”系统与“货到人”系统存在本质的差别,“人到货”系统中的订单分批及排序方法不能直接应用到“货到人”系统中。而且,现有的考虑货箱缓存区的订单排序问题中,未考虑商品订购数量与货箱中的商品存储数量。因此现有文献研究的问题与本文研究的场景不同,其结果不能直接解决本文的问题。
本文将在考虑订单中商品订购数量的前提下,研究设置货箱缓存区的AVS/RS系统订单分批拣选问题。考虑到同一批次的订单包含多种不同商品,且不同批次的订单中可能包含相同的商品,一方面在拣选每个批次订单时,需要出库多个货箱来满足该批次的商品需求,另一方面,拣选不同批次订单可能需要出库同一个货箱。通过在拣选台附近设置货箱缓存区,将使用频率较高的货箱暂存在货箱缓存区,减少其出入库次数。考虑到缓存区的容量有限,为了提高有限缓存区的利用率,应尽可能减少或避免长时间不用的货箱占用缓存区的情况发生。由于各个批次订单的拣选顺序直接影响货箱出库结果和缓存区的占用情况,在研究订单分批问题时,应同时考虑批次的拣选顺序、货箱出库方案以及出库货箱在缓存区的存放策略等,使得有限的缓存区得以高效利用,达到减少货箱出入库总次数、提高拣选效率的目的。
本文将建立该问题的联合优化模型,设计求解模型的三阶段启发式算法,并通过模拟计算验证模型和算法的有效性,进一步分析拣选台容量和缓存区容量变化对货箱出库总次数的影响,以及设置货箱缓存区的优越性。
1 自动小车存储及取货系统的工序流程
本文研究的自动小车存储与取货系统(AVS/RS)布局如图1所示,该系统主要包括存储区、输送区和拣选区。存储区由料箱式自动化立体仓库、多层穿梭小车、出入库缓存区和提升机组成,每个巷道旁的两排货架为一组,一组货架共用一套输送设备完成货箱的出入库操作,每层的穿梭小车负责货箱在储位与出入库缓存区之间的水平输送,提升机可以实现货箱在出入库缓存区与传送带之间的垂直输送;输送区主要包括出入库传送带与循环输送线,通过输送区把不同巷道的货箱输出至指定拣选台,或将已完成拣选任务的货箱输送回库;拣选区主要有拣选台、货箱缓存区与仓储信息设备等,每个拣选台可以同时拣选多个订单(即一批订单),拣选员通过系统仓储管理显示屏、灯光指引技术、电子标签技术等信息化辅助手段,根据订单中订购的商品从出库货箱或缓存区货箱中拣取相应的商品。

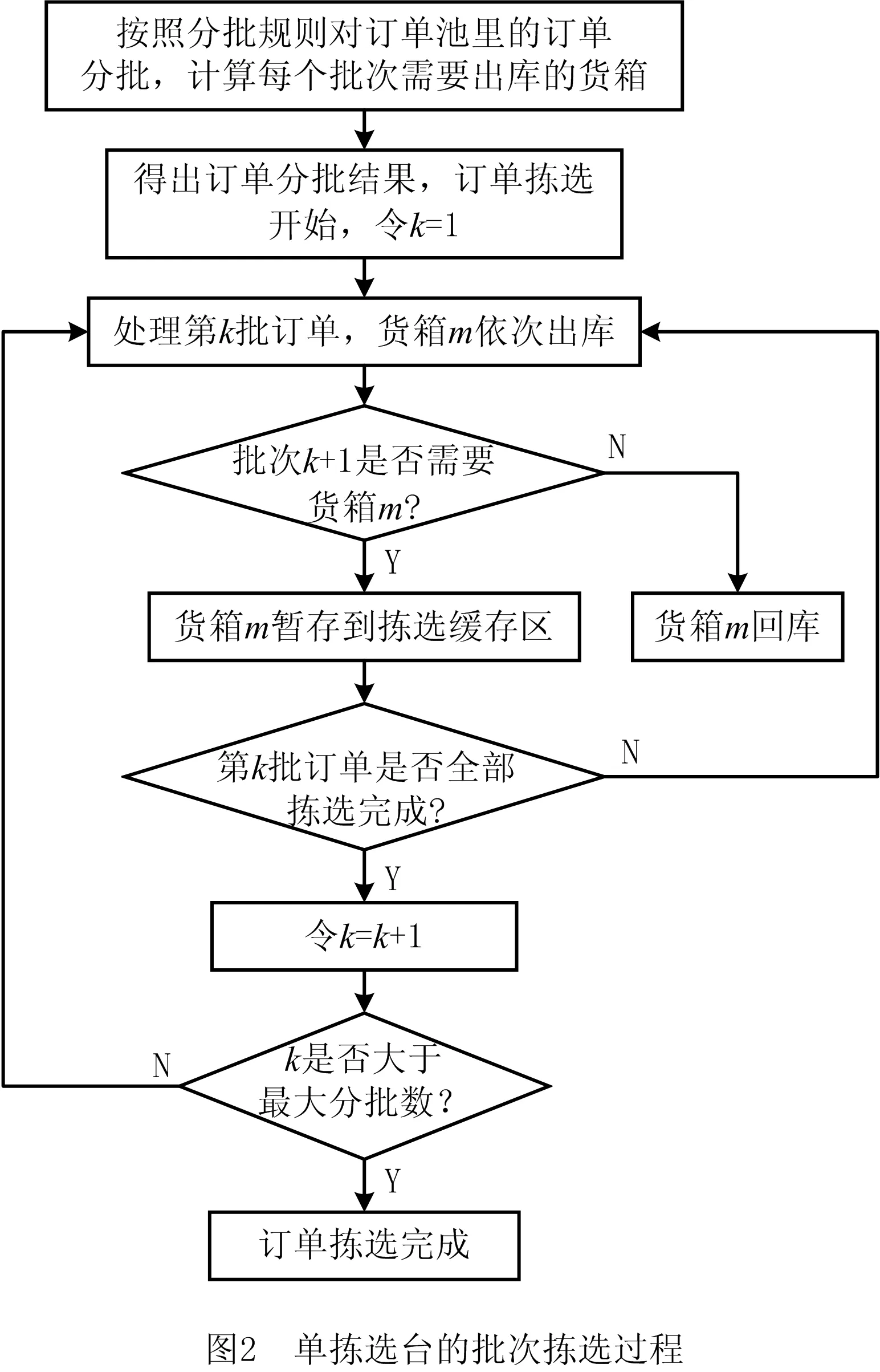
在设置货箱缓存区的AVS/RS系统中,当只有一个拣选台时,订单分批拣选过程如图2所示。首先按照某种分批规则对订单池内的订单进行分批,然后根据每个批次订单中包含的商品信息计算拣选该批次订单需要出库的货箱,通过穿梭小车、提升机与传送带等共同协作,将货箱输送到拣选台供拣选员拣取商品。当拣选第k批次时,系统将该批次需要使用的每个货箱m依次输送至拣选台,拣选完成后,根据拣选后续批次订单是否需要使用货箱m以及缓存区是否还有空余位置等信息,作出货箱是否需要回库的决策,将不需要回库的货箱m存放到货箱缓存区,将需要回库的货箱回库。若货箱m被存放在缓存区,且拣选第k+1批次时需要该货箱,则直接从缓存区调用货箱m,完成拣选后再次判断货箱m是否需要回库。
2 设置货箱缓存区的订单分批拣选问题数学模型
2.1 问题描述与分析
本文研究的设置货箱缓存区的AVS/RS包含一个拣选台,货箱缓存区最多可以同时存放H个货箱。已知仓库中M个货箱共存储了T种商品,一个货箱可存储一种或多种商品,已知每个货箱中存储的各种商品数量,且每个货箱中存储的各种商品总量不超过Q。 在一段时间内,配送中心共接到N个订单O={O1,O2,…,ON},已知每个订单Oi(i=1,2,…,N)中各种商品的数量Di=(di1,di2,…diT)(dit指订单i中商品t的需求数量)。由于拣选台空间限制,每个批次的订单数量不能超过C。 问题是如何将订单进行分批并确定批次拣选顺序,以及拣选每个批次的货箱出入库策略,才能使出库货箱总次数最小。
为了简化问题,本文作如下假设:
(1)每个订单箱只能容纳一个订单中的所有商品,拣选台可以同时容纳C个订单箱。
(2)系统使用标准化货箱,货箱的大小一样。货箱缓存区最多可以同时容纳H个货箱。
(3)假设仓库中每种商品的总库存量可以满足所有订单对该商品的总订购量,不考虑缺货的情况。
(4)每个货箱每次出入库时间相同,拣选员从货箱中拣取每件商品的时间相同,拣选员从货箱中拣取商品时的移动距离(时间)忽略不计。
基于以上假设,拣选所有订单的总时间可以表示为拣选订单中的商品次数和货箱出入库次数的函数。拣选订单中的商品次数与订单中商品总数量成比例,对于给定的待拣选订单,其中包含的所有商品总量为确定的常数,因此拣选订单中商品总时间为常数;在假设4下,货箱出库总次数越少,系统的拣选效率越高。因此,对于给定的待拣选订单,影响订单拣选效率的主要因素为货箱的出入库次数,本文的优化目标为最小化货箱出库总次数。
2.2 模型建立
本文模型符号和参数定义如下:
i为订单序号,i=1,2,…,N;
k为批次顺序,k=1,2,…,K;
m为货箱序号,m=1,2,…,M;
t为商品类别序号,t=1,2,…,T;
C为每个批次订单数量上限;

Q为每个货箱最大存储量;
H为货箱缓存区的容量;
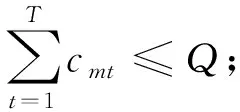
dit为订单i对商品t的需求数量;
决策变量定义如下:
smkt为拣选批次k时需要从货箱m中拣选的商品t数量。
建立混合整数规划模型(模型一):
(1)
s.t.
(2)
(3)
(4)
(5)
(6)
(7)
rmk≤ymk,∀k=1,2,…,K-1,∀m;
(8)
(9)
ym1=um1,∀m;
(10)
ymk=umk+rm,k-1,∀k=2,3,…,K,∀m;
(11)
(12)
xik,ymk,umk∈{0,1},∀i,m,k;
(13)
rmk∈{0,1},∀m,k=1,2,…,K-1;
(14)
smkt∈Z+,∀m,k,t。
(15)
其中:目标函数(1)表示使货箱的出库总次数极小化。约束条件(2)表示任意一个订单恰好被分配到一个批次中;约束条件(3)表示每个批次包含的订单数量不超过拣选台容量;约束条件(4)表示每个批次中包含的每种商品总需求量与从出库货箱中拣选的该商品总量相等;约束条件(5)表示如果拣选批次k时,从货箱m中拣取了某种商品,则决策变量ymk=1;约束条件(6)表示如果拣选批次k时没有从货箱m中拣取任何商品,则决策变量ymk=0;约束条件(7)表示从任意货箱m中拣取同一种商品t的总数量限制;约束条件(8)表示只有拣选批次k时使用了货箱m,货箱m才有可能在拣选完批次k之后被存入缓存区;约束条件(9)表示拣选批次k之后被存入缓存区的货箱m一定会在后续批次拣选中被使用;换言之,对于后续批次中均不需要使用的货箱,不必存入缓存区;约束条件(10)表示拣选第1批次需要使用的货箱只能是出库货箱;约束条件(11)表示拣选第2到K批次需要使用的货箱一定是缓存区存放的货箱或出库货箱;约束条件(12)表示拣选完任意批次k之后存入缓存区的货箱总数不能超过缓存区总容量;约束条件(13)~(15)为决策变量取值约束。
订单分批拣选联合优化问题的混合整数规划模型中同时包含了订单分批决策、批次排序决策、拣选每个批次需要出库的货箱和从每个货箱中拣取的商品数量,以及需要存入缓存区的货箱等决策。通过求解该模型可以得到使出库货箱总次数达到最小的订单分批拣选方案。
例1已知8种商品存储在10个货箱中,具体存储信息如图3所示,英文字母表示商品种类,数字表示存储量。
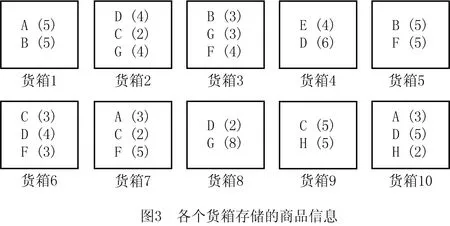
假设某段时间内收到12个订单, 每个订单中订购的各种商品及数量如下,其中括号中的数字表示商品的订购数量:
O1={A(1),C(2)},O2={A(1),F(2)},O3={A(1),B(1),C(1)},O4={C(1),H(1)},O5={B(1),D(1)},O6={D(1),E(1)},O7={F(1),G(2)},O8={F(2)},O9={B(1),D(1),E(1)},O10={D(3)},O11={B(2),F(1)},O12={G(1),H(1)}。
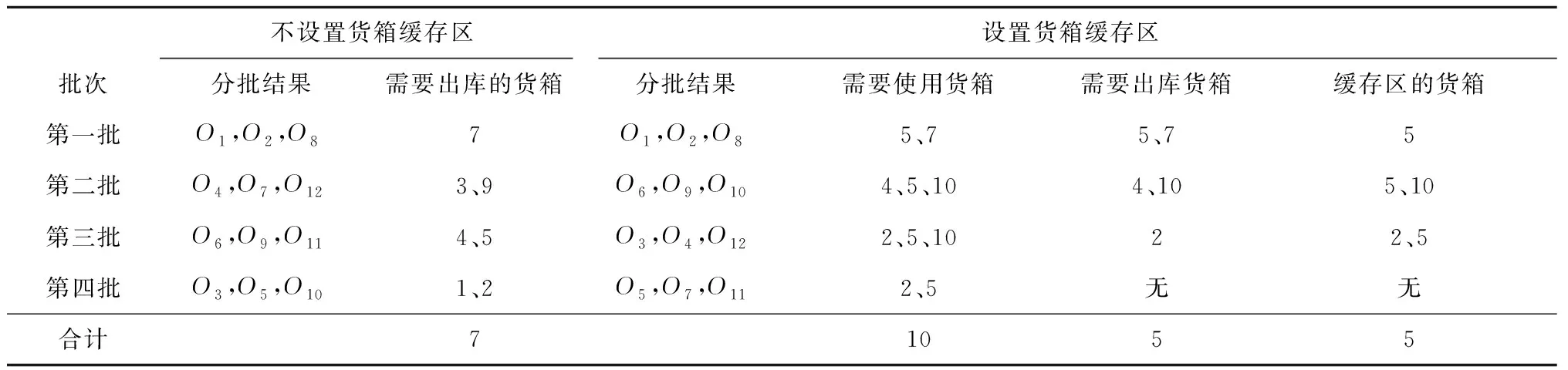
已知拣选台容量C=3,货箱缓存区容量H=2,利用GUROBI软件求解混合整数规划模型,得到最优分批拣选策略如表1所示。12个订单被分为4个批次,表1中第1列给出了每个批次的拣选顺序,第2列表示每个批次中包含的订单集合,第3列表示拣选每个批次订单需要使用的货箱集合,第4列表示拣选每个批次订单需要出库的货箱集合,第5列表示拣选完每个批次之后需要存入缓存区的货箱集合。按照表1所示的最优拣选策略,第一批次包含订单O1,O2,O8,拣选该批次订单需要使用货箱5、7,出库货箱为5、7;第一批次拣选完成之后,货箱5被存入缓存区,供拣选后续批次订单使用。第二批次包含订单O6,O9,O10,拣选该批次需要使用货箱4、5、10,由于货箱5已经在缓存区,所以只需再出库货箱4、10;第二批次拣选完毕后,将货箱10存入缓存区,此时缓存区存放的货箱为5、10;第三批次包含订单O3,O4,O12,拣选该批次订单需要使用货箱2、5、10,其中货箱5、10直接从缓存区调用,因此只需要出库货箱2即可;拣选完第三批订单之后,货箱2、5被存入缓存区;拣选第四批订单O5,O7,O11需要使用货箱2、5,由于货箱2、5均在缓存区,所以直接调用,不需要再出库其他货箱;第四批次订单拣选完毕后所有货箱回库。按照以上方案分批拣选,总共需要出库货箱5次。
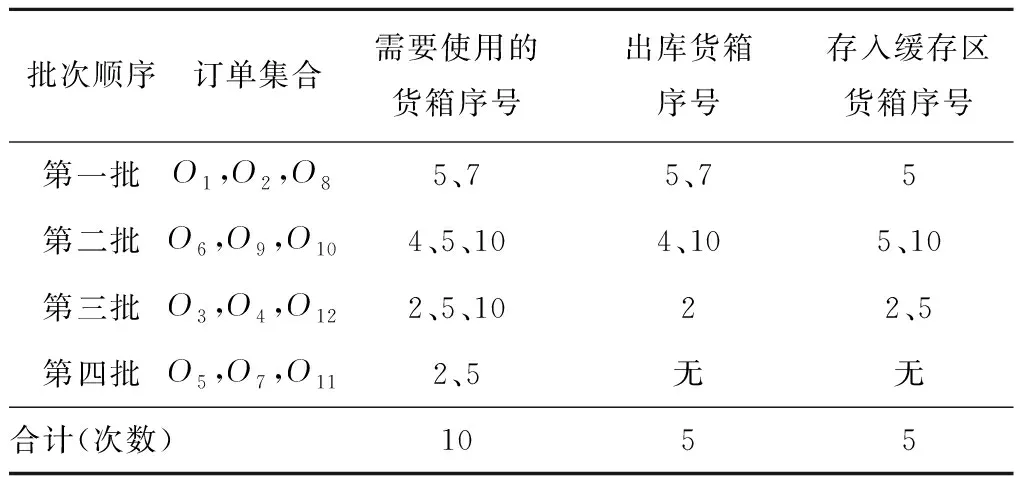
表1 示例对应的最优订单分批拣选方案
如果不设置货箱缓存区,仍然按照表1中的订单分批结果进行拣选,则拣选4个批次订单需要出库货箱的总次数为10次(实际上,在不设置货箱缓存区的情况下,最优分批结果与表1中的分批结果可能不同,本文将在4.4节中进行讨论);由以上分析可以发现,通过设置货箱缓存区,有效避免了同一货箱在不同批次拣选时重复出入库的操作,使货箱出库总次数减少了50%,大大提高了拣选效率,降低了拣选成本。
3 启发式算法
订单分批拣选问题可以分解为订单分批、批次排序、确定拣选每个批次的货箱出入库方案等3个相互关联的子问题。其中订单分批问题本质上是对订单进行聚类,将关联度较大的订单划分到一个批次中[27];确定服务每个批次需要使用的货箱集合可以归结为集合覆盖问题;确定分批后的批次拣选顺序问题可以归结为排序问题或带约束的旅行商问题,以上子问题均属于NP-hard问题。因为实际中,订单分批拣选问题属于运作层面的决策问题,需要在短时间内给出方案,所以需要设计快速有效的求解算法。本章将结合问题数学模型的结构特征,设计三阶段启发式算法。
3.1 计算订单之间的加权相似度
利用订单之间的加权相似度进行分批的基本思想为:通过订单中包含的商品种类与商品在货箱中的存储位置信息,分别计算任意两个订单之间的品项相似系数与储位相似系数,再根据给定的权重,计算订单之间的加权相似度;根据订单之间的加权相似度,利用贪婪规则对订单进行聚类,尽可能地将加权相似度大的订单分在一个批次中,从而减少货箱的总出入库次数。
首先借鉴文献[6]提出的巷道相似系数,将任意两个订单中订购的相同商品种类数占两个订单中的总商品种类数的比例,定义为两个订单之间的品项相似系数,即订单Oi和订单Oj的品项相似系数
式中Fi为订单Oi中的商品种类集合。
然后,定义订单之间的储位相似系数。在AVS/RS系统中,由于一个货箱可能存储多种商品,出库一个货箱可以同时拣选多种商品,满足一个或多个订单中的商品需求。给定任意两个订单,根据两个订单中商品占用相同货箱的比例,定义订单之间的储位相似系数[28]。
令VAi=(a1i,a2i,…aMi)表示订单Oi的商品占用货箱信息,其中
ami=
计算订单之间的加权相似度。对于给定的加权系数ω(0≤ω≤1),加权相似度
利用上式分别计算任意两个订单之间的加权相似度,则加权相似矩阵可以表示为:
其中gij表示订单Oi和订单Oj的加权相似度。为了方便计算,当i=j时,令gij=0。
从加权相似度的定义可以看出,加权系数ω的取值直接影响加权相似度的计算结果。本文直接根据从货箱中拣取一件商品的成本和出库一个货箱的成本之比,确定加权系数ω的取值[29]。
3.2 三阶段启发式算法
本节将基于订单分批拣选联合优化问题包含的3个子问题,设计三阶段启发式算法。第一阶段利用贪婪算法求出订单分批结果,分别计算拣选每个批次需要使用的货箱集合;第二阶段求解各个批次的拣选顺序;第三阶段确定拣选每个批次时需要出库的货箱和拣选之后需要放入缓存区的货箱。
3.2.1 第一阶段:设计贪婪算法求出订单分批结果及拣选每个批次需要使用的最少货箱集合
利用加权相似度矩阵,设计贪婪算法求解订单分批结果,并确定拣选每个批次需要使用的最少货箱集合,本阶段算法分为以下3步:
步骤1生成初始订单分批结果。
步骤1.1 设置参数ω,得到加权相似度矩阵G。
步骤1.2 从矩阵G中寻找最大相似度系数gij及相应的订单i与订单j。 若gij<0,则转步骤1.6;否则,转步骤1.3。
步骤1.3 根据以下4种可能出现的情景,为订单i与订单j指派批次:
(1)两个订单均被指派批次,则转步骤1.4。
(2)恰有一个订单被指派批次,则将另一个订单指派到相同的批次中,转步骤1.4。
(3)两个订单均未被指派批次,且现有的非空批次数量小于K,则开启一个新批次,并将两个订单同时指派到新批次中,转步骤1.4。
(4)订单i与订单j均未被指派批次,且现有的非空批次数量等于K。 此时,如果能够找到一个批次,其中包含的订单数量小于C-2,则将两个订单同时指派到该批次中;否则将两个订单指派到任意两个包含C-1个订单的批次中,转步骤1.4。
步骤1.4 将已指派批次的两个订单之间的相似度gij修改成-1。
步骤1.5 检查每个批次中的订单个数q是否达到上限C。
若q=C,则该批次中的订单个数已达到上限,将该批次中各个订单对应的加权相似度系数均修改为-1,转步骤1.2;如果q 步骤1.6 结束,输出初始订单分批结果x0。 步骤2计算拣选每个批次订单需要使用的最少数量货箱集合。 步骤2.1 用Pk=(pk1,pk2,…,pkT)表示批次k中所有订单订购的各种商品总数量,其中元素pkt代表批次k中订购商品t的总数量。令k=1,转步骤2.2。 步骤2.2 按下列公式选择包含批次k中尚未拣选商品数量最多的货箱m*: 更新货箱m*中剩余的商品存储量和批次k中尚未满足的商品需求量: cm*t=cm*t-min{cm*t,pkt},∀t; pkt=pkt-min{cm*t,pkt},∀t。 步骤2.4 令k=k+1,若k≤K,转步骤2.2;否则,转步骤2.5; 步骤2.5 计算结束,输出拣选每个批次需要使用的货箱集合(对应决策变量y0),计算拣选所有批次需要使用的货箱总数量z0。 步骤3利用邻域搜索方法改进订单分批拣选初始方案x0和y0,以减少拣选过程中使用货箱总次数z0。 输入:贪婪算法求得的订单分批拣选初始方案x0和y0,拣选所有批次需要使用的货箱总次数z0;设置最大迭代次数Lmax,移除操作D,插入操作R。 输出:近似最优分批拣选方案x*=xc,y*=yc,目标函数值z*=zc。 初始化:当前解与当前目标函数值分别设置为:xc=x0,yc=y0,zc=z0,迭代次数l=0。 当l≤Lmax时,循环执行步骤3.1~步骤3.3 步骤3.1 在初始分批结果中随机选取20%的批次,在每个批次中任意移除一个订单,生成破坏解xdestroy。 将已经移除的订单放到集合U中,等待重新分配批次。 步骤3.2 按照贪婪插入规则为被移除的订单i∈U重新指派批次,生成邻域解xrepair。 具体方法为:对于每一个订单i∈U,计算其与破坏解xdestroy中每个未饱和批次中各个订单的平均相似度,将订单i重新指派到平均相似度最大的批次中。 步骤3.3 计算邻域解xrepair对应订单分批结果,拣选每个批次需要使用的货箱信息yrepair,以及拣选所有批次需要使用的货箱总数量zrepair。 若zrepair 令l=l+1,转步骤3.1。 3.2.2 第二阶段:利用邻域搜索方法生成批次拣选顺序,使相邻两个批次使用的相同货箱数量之和达到最大 首先,利用贪婪算法生成各个批次的初始拣选顺序π:任意选择一个批次作为拣选序列中的第一个批次,按照贪婪规则,从未排序的批次中依次选择与拣选序列中最后批次共用货箱数量最多的批次加入拣选序列中,直到所有批次均加入序列中,生成初始可行解π。 然后,采用两种局部搜索方法生成邻域解,利用模拟退火机制逐步改进当前解,得到近似最优解。本节采用的两种生成邻域解的操作分别是插入操作(改变π中的某一批次在序列中的位置)与交换操作(将π中的两个批次在序列中位置进行交换)。 算法具体步骤如下: 输入:初始可行解π、初始温度τ、降温速率λ、最大迭代次数Tmax、插入概率p; 输出:近似最优解πb。 步骤1利用贪婪算法生成各个批次的初始拣选顺序π,计算按照该顺序拣选时,相邻两个批次之间共用货箱的总次数f(π)。 步骤2初始化当前解与及对应的目标函数值,令πc=π,f(πc)=f(π)。 初始化最优解与最优目标函数值,令πb=π,f(πb)=f(π)。 步骤3当t≤Tmax时,循环执行以下(1)~(4)的操作: (1)以概率p执行插入操作,否则执行交换操作,得到邻域解π′,并计算其对应的目标函数值f(π′); (2)若f(π′)>f(πc),则更新当前解与当前值;否则以一定的模拟退火概率接受邻域解; (3)若f(πc)>f(πb),则更新最优解与最优值,令πb=πc,f(πb)=f(πc)否则不更新。 (4)更新当前温度与当前迭代次数,令τ=τ·λ,t=t+1。 3.2.3 第三阶段:确定按近似最优解顺序拣选每个批次时,实际出库的货箱、放入缓存区的货箱及货箱出库总次数(整数规划的目标函数值) 输入:拣选各个批次k需要使用的货箱集合Yk={m|ymk=1,m∈M},k∈K; 步骤1令R0=∅,即货箱缓存区初始状态为空;令k=1,对任意的m∈M,令um1=ym1,U1=Y1, 表示拣选第1批次订单需要使用的货箱均为出库货箱。 步骤3对Uk∪Rk-1中的货箱,按照em值由小到大排序,依次选择em值较小的前min{H,|Uk∪Rk-1|}个货箱存入缓存区,对于每个被选中的货箱m,令rmk=1;计算拣选批次k之后存入缓存区的货箱集合Rk={m|rmk=1}。 步骤4计算拣选第k+1批次需要出库的货箱集合Uk+1={m|m∈Yk+1且ym,k+1-rmk=1}。 对∀m∈Uk+1,令um,k+1=1。 步骤5若k+1 为验证本文模型与算法的有效性,本章设计多个算例进行模拟计算。对于规模较小的算例,利用GUROBI求解器求解混合整数规划模型得到的精确最优解与启发式算法求得的近似最优解进行对比,分析启发式算法的求解效果。当算例规模增大时,GUROBI求解器无法在可接受的时间内求出精确最优解,为此本文设置固定的运行时间,并比较GUROBI求解器在给定的运行时间内得到的最好解与启发式算法求得的近似最优解的差异。对于每个算例,分别记录两种算法的运行时间,并进行对比分析。最后,针对拣选台容量和货箱缓存区容量变化对最优解的影响进行了灵敏度分析,并将设置货箱缓存区的订单分批拣选模型与不设置货箱缓存区的订单分批拣选模型进行比较,分析设置货箱缓存区的优越性,并提出确定缓存区容量的思路。 设置商品种类数T、货箱个数M、订单数量N等3个参数的不同取值生成28组算例。设拣选台容量C=3,货箱缓存区容量H=2。 每个货箱容量Q=20,每个货箱中最多存储4种商品;每个订单中订购的商品种类为1~4种,每种商品的订购量为{1,2,3,4,5}的任意取值。 本节将通过小算例分析启发式算法的求解精度与计算时间。对于每一个算例,先利用GUROBI求解混合整数规划模型得到精确最优解,再利用启发式算法运算10次,得到近似最优解,取启发式算法10次运算的平均值与精确最优解进行对比。 启发式算法的参数设置如下:相似度加权系数ω=0.5,第一阶段迭代次数Lmax=100,模拟退火的初温τ=200,降温速率λ=0.9,第二阶段最大迭代次数Tmax=200,生成邻域解的插入概率p=0.2。 本文使用GUROBI 9.0.2求解混合整数规划模型;利用MATLAB编程实现三阶段算法,并在Inter Core i5-8 265U笔记本电脑运行。 首先,将启发式算法10次运算求得的平均结果与利用GUROBI求解器得到的精确解进行对比,分析启发式算法的近似比。表2列出了两种方法的详细求解结果。在每个算例中,精确解均优于启发式算法的平均值,启发式算法平均值的近似比不超过1.4。启发式算法的平均求解时间均在3 s以内,而GUROBI的求解时间随问题规模的增大呈指数增长,对于很小的算例可以在1 s以内求得最优解,随着问题规模的增大,GUROBI的求解时间远远大于启发式算法的平均求解时间。 表2 小规模算例的求解结果分析 随着算例规模的增大,GUROBI的求解时间越来越长,对于中等规模的问题,求解器无法在2 000 s内得到精确最优解。由于订单分批拣选问题属于运作管理问题,需要在短时间内作出决策,假设实际中可接受的最长决策时间为2 000 s。设定GUROBI求解器的运算时间为2 000 s,将求解器在2 000 s内得到的最好解与启发式算法求出的近似最优解进行对比,分析启发式算法的求解效果,详细结果如表3所示。从表3可以看出,对于所有的算例,启发式算法的最长平均求解时间不超过90 s。其中,只有对订单数量为50或商品数量为20且订单数量为100的4个小算例,求解器在2 000 s之内得到了比启发式算法更好的解,对于其余的16组算例,特别是订单数量超过100的所有算例,启发式算法得到的近似最优解均明显优于GUROBI求解器在2 000 s内得到的最好解。当固定商品数量和货架数量时,随着待拣选订单数量的增加,启发式算法的优越性越来越明显。 表3 中等规模算例的计算结果分析 对于给定的待拣选订单,一些参数的变化会对订单分批拣选结果产生直接的影响。拣选台容量决定了一个批次中可以同时拣选的订单数量,货箱缓存区容量决定了批次之间共用货箱中不需要回库的货箱最大数量,本节分别对拣选台容量和货箱缓存区容量变化对货箱出库总次数的影响进行灵敏度分析。 (1)拣选台容量C的变化分析 为了分析拣选台容量C的变化对货箱出库总次数的影响,固定货箱缓存区容量H=2,选取参数为T=30,M=30,N=100和T=50,M=50,N=50的两个算例。对于每一个算例,让拣选台容量C依次取2~6之间的整数,分别计算不同拣选台容量下的最优分批拣选方案对应的货箱出入库总次数,结果如图4所示。 由图4可以看出,随着参数C的增大,货箱出入库次数逐渐减小。这是因为参数C越大,每个批次包含的订单数量越多,一个货箱出库平均可满足的订单数量越多;另一方面,参数C越大,批次数越少,同一货箱的平均出库次数减少,因此货箱的总出库次数也会减少。 (2)货箱缓存区容量H的变化分析 为了分析货箱缓存区容量H对货箱出库次数的影响,仍然以T=30,M=30,N=100和T=50,M=50,N=50的例子进行计算,固定拣选台容量C=3,让货箱缓存区的容量H从1变化到10,分别求解订单分批拣选问题,记录货量出库总次数,具体结果如图5所示。由图5可以看出,当H从1增大到4时,算例1的货箱出库次数减少得较明显,当H>4时,出库次数减少的幅度下降。这是由于算例1中不同批次共用的货箱数较少,当H大于任意两个批次之间共用的货箱最大数量时,继续增大货箱缓存区容量已经毫无意义。在算例2中,随着H的增大,货箱出库总次数单调减少,且减少趋势与算例1类似。当H≤5时,货箱出库次数下降较快,当H>5时,货箱出库次数下降缓慢。实际中,由于增大货箱缓存区容量需要一定的空间与成本,当缓存区容量达到一定规模以后,必然出现效益递减的情况,因此,不应该盲目增大缓存区容量。 从灵敏度分析结果可以看出,随着货箱缓存区容量的增大,拣选所有订单需要出库货箱的总次数单调递减。当货箱缓存区容量等于0时,设置货箱缓存区的订单分批拣选问题转化为不设置货箱缓存区的订单分批拣选问题。本节将对比分析两情况下的求解结果。 对于不设置货箱缓存区的订单分批拣选问题,拣选任意一个批次k需要使用的货箱与需要出库货箱完全相同,因此不设置货箱缓存区的订单分批拣选问题的优化目标等于拣选每个批次需要使用的货箱数量之和。为方便对比分析,仍然使用2.2节中定义的符号和变量,不设置货箱缓存区的订单分批拣选问题可以表示为如下混合整数规划模型(模型二): (16) s.t. (17) (18) (19) (20) (21) xik,ymk∈{0,1},∀i,m,k; (22) smkt∈Z+,∀m,k,t; (23) 2.2节中的模型(模型一)与本节不设置货箱缓存区的订单分批模型(模型二)的目标函数均为最小化货箱出库总次数,但由于模型二中不设置货箱缓存区,拣选每个批次需要使用的货箱即为要出库的货箱。模型一的约束(2)~约束(5)、约束(7)与模型二的约束(17)~约束(21)含义相同。但两个模型存在以下区别:首先,模型二不需要考虑批次顺序,符号k在模型二中既可以理解为批次索引,也可以理解为批次顺序索引,在模型一中则表示批次顺序索引;模型一要考虑拣选每个批次时,需要出库的货箱、和需要放入缓存区的货箱,因此模型一引入了两个决策变量umk与rmk,其中umk表示拣选第k个批次时是否让货箱m出库,rmk表示拣选完第k个批次后是否把货箱m放入货箱缓存区,通过约束条件(8)~约束(12),表示能够存入货箱缓存区的货箱需要满足的约束以及拣选批次订单需要使用的货箱与缓存区内货箱之间的关系,而模型二中不需要考虑这5个约束及相关的变量;同时,模型一为了有效利用缓存区的容量,避免不需要的货箱提前出库占用缓存区,引入了约束条件(6)限制拣选批次k时需要出库的货箱必须是批次k中需要使用的货箱。通过以上分析可以看出,设置货箱缓存区的订单分批模型中决策变量和需要考虑的约束条件更多,不设置货箱缓存区的订单分批模型可以看成设置货箱缓存区的订单分批模型的特殊情况(即H=0的情况)。下面通过一个具体例子,分析两种模型的求解结果。 例2已知商品存储信息、每个订单中订购的商品信息和拣选台容量等与2.2节示例相同,假设系统不设置货箱缓存区。利用GUROBI求解混合整数规划模型(模型二),得到如下分批结果:第一批包含订单O1,O2,O8,第二批包含订单O4,O7,O12,第三批包含订单O6,O9,O11,第四批包含订单O3,O5,O10。 与2.2节例1中设置货箱缓存区的订单分批模型求解结果相比,订单分批结果与货箱出库情况均发生了变化(其中2.2节例1有多个最优解,本节只对比其中一个最优解)。不设置货箱缓存区的订单分批拣选方案与设置货箱缓存区的订单分批拣选方案如表4所示。由表4可以看出,不设置货箱缓存区时一共需要出库货箱7次,设置货箱缓存区时只需要出库货箱5次。 表4 两种模型求解结果对比 分析表4的结果可知,在不设置货箱缓存区的中,每个批次之间无共用的货箱,且每个批次需要使用的货箱与出库货箱相同,拣选4个批次需要使用的货箱总数为7个。相比之下,设置货箱缓存区的系统中,拣选每个批次需要使用的货箱数明显增多,拣选所有批次需要使用的货箱总数为10个,但拣选相邻批次可以共用的货箱数量较多,通过将相邻批次共用的货箱存入缓存区,可以有效减少实际出库的货箱数量,本例中实际出库货箱数量为5,比不设置货箱缓存区的情况减少了28.6%。以上研究结果表明,对于给定的待拣选订单集合,与不设置货箱缓存区的系统相比来说,设置货箱缓存区的拣选系统可以使货箱的总出库次数明显较少,从而达到降低货箱出库成本、缩短拣选作业时间的效果。 考虑到设置货箱缓存区需要支付一定的固定成本,结合对货箱缓存区容量的灵敏度分析,可以进一步确定最优缓存区容量,使整个系统的总运行成本达到最小。 本文针对设置货箱缓存区的AVS/RS系统中的订单分批拣选问题,考虑订单中商品订购数量与货箱中商品存储数量,选取货箱出入库次数作为刻画系统拣选效率的主要指标,以出库货箱总次数最小化为目标建立了订单分批拣选联合优化问题的整数规划模型,并设计了求解模型的三阶段启发式算法。通过设计不同规模的算例,验证了本文模型与算法的正确性与有效性。进一步分析了拣选台容量与货箱缓存区容量变化对货箱出库次数的影响。 通过对比分析设置货箱缓存区与不设置货箱缓存区的订单分批拣选问题数学模型结构,证明了设置货箱缓存区的问题是不设置货箱缓存区情况的一般化推广。通过具体实例分析,证明了设置货箱缓存区的系统可以减少货箱出库总次数,提高订单拣选效率。 本文研究设置货箱缓存区的AVS/RS订单分批问题时,只考虑了单拣选台的情况,实际中可能存在多个拣选台。当多个拣选台之间的距离较远时,货箱缓存区不能共用,此时的问题可以分解为多个单拣选台的子问题。当多拣选台之间距离较近,且相邻的拣选台可以共用货箱缓存区中存放的货箱时,问题将变得更加复杂,此时需要综合考虑订单分批问题、多个拣选台之间的任务分配问题、各个拣选台的任务排序问题等,并协调多个拣选台的出库货箱与缓存区内货箱的存取及调度等问题,未来可以结合这些场景,对问题进行深入探究,建立更加符合实际的模型。下一步,可以针对本文建立的订单分批拣选模型结构特征,设计求解模型的精确算法并进行理论分析,为设计更多的快速有效近似算法提供理论基础。
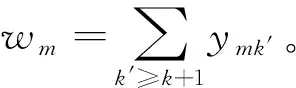
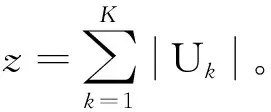
4 模拟计算与结果分析
4.1 参数设置与算例生成
4.2 小算例计算结果与分析
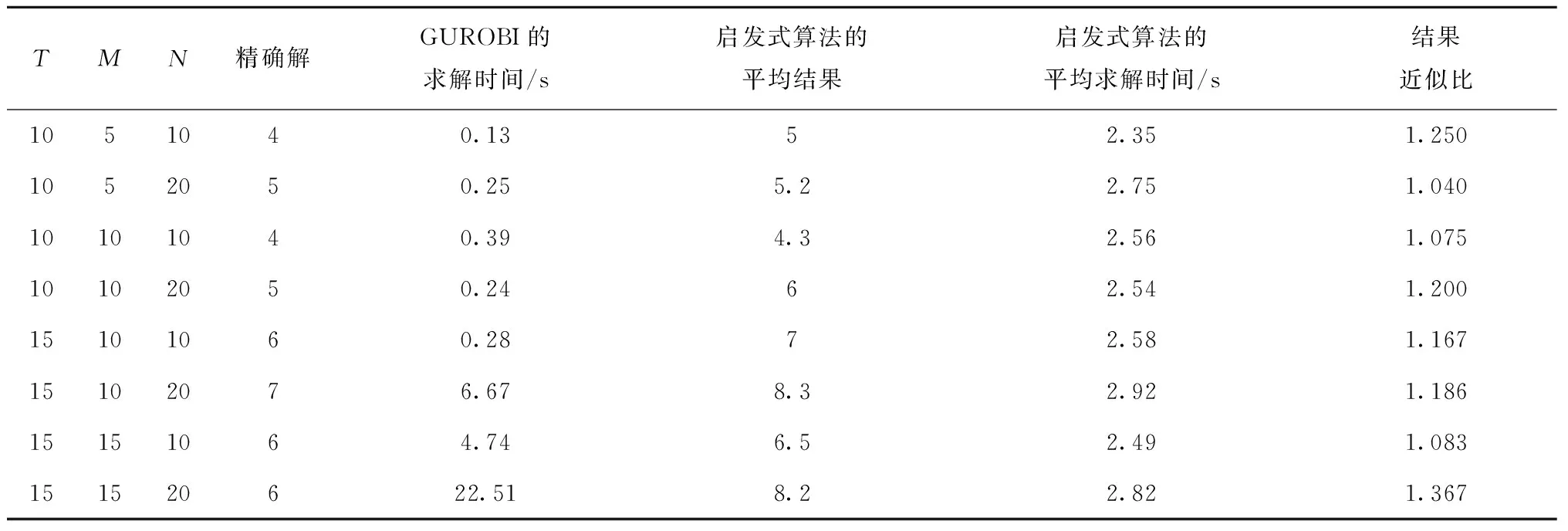

4.3 灵敏度分析
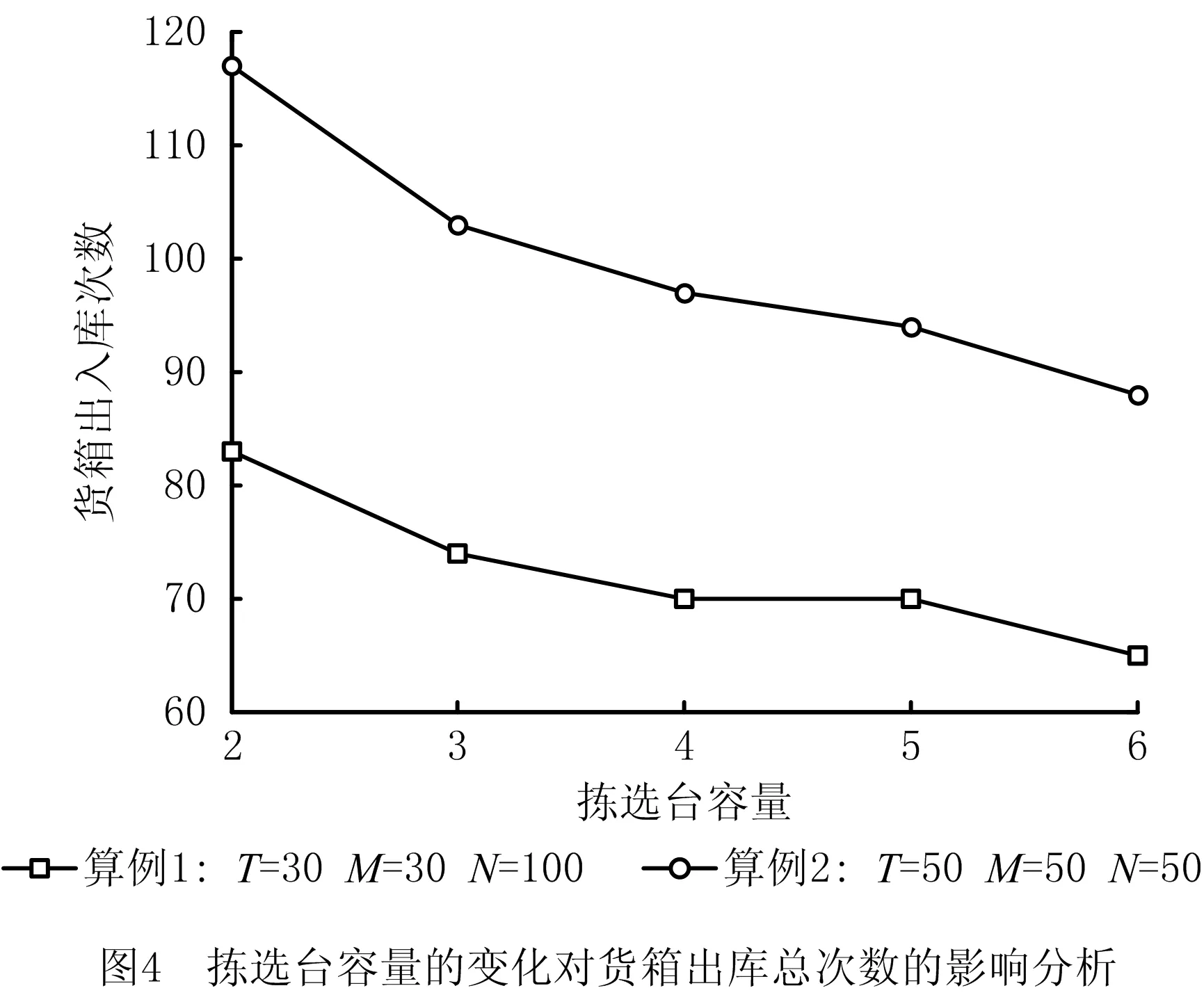

4.4 与不设置货箱缓存区的订单分批模型对比分析
5 结束语
