面向大规模立体仓库货位分配问题的两阶段混合优化算法

黄 鹏，姚锡凡，胡晓阳，曾中荣

(1.华南理工大学 机械与汽车工程学院，广东 广州 510640；2.广东世创金属科技股份有限公司，广东 佛山 528300)

0 引言

新技术和新业态的高速发展及产品生产周期不断缩短，迫使许多制造企业向智能化转型。智能工厂是智能制造和企业智能化转型的核心主题之一。立体仓库作为连接生产与销售间物料流转的重要环节之一，是智能工厂的重要组成部分，受到许多研究者的关注。相对传统的仓储方式，立体仓库有许多优点，如节约劳动力成本与建筑面积，提升仓库作业效率，提升仓储作业的可靠性和稳定性[1-2]。如何让立体仓库更快速地响应销售和生产的需求是当前仓储行业的研究热点之一，其中制约仓库作业效率的主要因素之一就是货位分配的质量。

大量的智能优化算法被用于求解仓库中的优化问题[3-4]。根据REYES等[5]在货位分配问题上的研究结论，许多文献使用遗传算法(Genetic Algorithm, GA)、禁忌搜索(Taboo Search, TS)等元启发式方法优化求解仓库货位分配问题。货位分配优化问题中常见的优化目标是出入库效率最高、货架稳定性最大、产品关联度高、能耗最小等。曹现刚等[6]、ZHANG等[7]和郭娟等[8]都针对立体仓库货位分配问题建立考虑出入库效率、货架稳定性和货物相关性的多目标模型。其中：曹现刚等[6]和ZHANG等[7]都采用了改进遗传算法求解货位分配优化模型，曹现刚等[6]在遗传算法中融合模拟退火机制增强遗传算法的搜索能力；ZHANG等[7]在遗传交叉和变异中采用了自适应算子以提升子代解的质量；而郭娟等[8]采用了融合非支配排序方法的粒子群算法求解多目标货位分配模型，并对改进粒子群算法进行了案例验证。ENE等[9]则关注立体仓库作业能量消耗问题，建立了最小化能量消耗的货位分配优化模型，采用了遗传算法对该模型进行优化求解，以满足立体仓库的环保节能需求。刘恺文等[10]针对立体仓库作业过程建立了能量消耗模型，采用一种基于levy飞行搜索策略的改进灰狼算法对立体仓库作业能量优化模型进行求解，并通过仿真实验验证了其算法的有效性。

除了上述优化原则外，许多研究人员在货位分配优化问题中考虑仓储流程约束和仓库物理空间约束，建立了更加切合实际情况的货位分配优化模型；TU等[11]在货位分配优化模型中添加拣货负载均衡和补货时间约束，提出了启发式多目标遗传算法对模型进行优化求解，并结合案例验证了该算法的有效性；YANG等[12]建立了集成存取作业调度的货位分配优化模型，针对不同规模的优化问题设计了不同的禁忌搜索算法，并对算法参数的敏感性进行实验分析；唐文献等[13]针对船舶工业立体仓库，考虑物品分巷道存储原则，提出一种细菌觅食算法求解多目标货位分配模型；XIE等[14]针对分组约束的货位分配问题提出一种邻域受限的邻域搜索算法，并对比了数学规划法，结果显示其设计的算法性能更加优异，是一种有效求解带分组约束货位分配问题的算法；GUERRIERO等[15]和QUINTANILLA等[16]将仓库空间利用率视为货位分配问题的优化目标，并设计了启发式、元启发式及局部搜索算法求解货位分配优化问题，验证了局部搜索算法能够解决货位分配优化问题；HE等[17]开发了一种基于邻域变异算子的粒子群算法求解带空间顺序约束的货位分配问题，并对该算法进行了数值实验，其实验结果显示，带有扰动的邻域变异算子能够有效地跳出局部最优解，增强了算法的全局搜索能力；蔡安江等[18]则研究了双出口立体仓库货位分配问题，提出一种改进蛙跳算法求解多目标货位分配模型，并通过实验验证了该算法的有效性。

不难发现，许多货位分配优化文献将出入库效率、货架稳定性、货物相关性或空间利用率作为优化重心，而忽略了货架间货物分布的失衡和堆垛机负载均衡问题。此外，立体仓库货位分配问题的研究大量应用元启发式智能优化算法，如遗传算法等。然而，智能优化算法的优点和缺陷都比较明显，实际应用需要考虑各个算法的特性，如算法的收敛速度、适用问题规模等因素。针对货位分配这类离散优化问题而言，连续型智能优化算法需要在求解过程中设计离散化环节。离散化环节需要特别关注，因为不合理的离散化可能会抑制优化算法的性能。同时，一些研究表明，针对离散优化问题开发有效的局部搜索算子增强算法的局部搜索能力是极其重要的[16-17]。延迟接受爬山(Late Acceptance Hill-Climbing, LAHC)算法在车间调度领域被证明是一种高效的迭代邻域搜索算法[19]，而在货位分配问题上却没有得到有效运用。考虑当前的研究现状，本文建立了考虑堆垛机负载均衡的多目标立体仓库货位分配优化模型，并提出一种集成GA和LAHC算法优势的两阶段混合优化算法。通过仿真实验结果表明，该两阶段混合算法较好地集成了GA算法的全局探索能力和LAHC算法的强大局部搜索能力，能够有效解决立体仓库货位分配问题。

1 场景及数学建模

立体仓库主要由货架、堆垛机、出入库平台和运输设备(自动导引小车、传送带、升降机等)组成。S金属公司是广东一家大型的金属加工与设备生产企业，该公司计划在其新厂区建设一个中型立体仓库，用于厂内物料中转。该公司计划建设的立体仓库布局与YUE等[20]所提及的仓库相似，但是将立体仓库的仓储部分与物料流动环节进行了重新布局，以节省更多建筑面积。如图1所示，立体仓库的存储区域与物料处理区域分布在不同的楼层，二者通过升降机实现物料转移与流通。物料处理楼层包含了DE KOSTER等[21]所提及的接收、打包、拣选等主要仓储活动。在物料处理过程中大量应用自动导引小车(Automated Guided Vehicle, AGV)，以减少传送带的使用，提升仓库的物料转运的柔性度。就单个货架而言，货架的出入库平台与升降机相连，实现货架与物料处理层的链接与流转。

货位分配作为仓储流程的起点，其结果的好坏会对后续环节产生影响[22]。合理的货位分配与设置是提升立体仓库仓储效率的关键之一。货位分配主要为入库物料安排恰当合理的仓储货位，以提升后续仓储操作的效率。货位分配问题是分配问题的变种之一，已被证明是NP-Hard问题[23]。为了更好地管理仓库，提升仓库作业效率，大量的货位分配策略被提出，如“最短路径”、“重心最低”、“先进先出” 等。这些分配策略体现了仓库管理者对仓库不同性能的重视程度，即仓库运作过程中的优化目标。为了使立体仓库更好地适应公司的实际需求，本研究在货位分配中的优化目标主要基于效率最高原则、货架稳定性原则和堆垛机负载均衡原则。

1.1 模型建立

假设立体仓库有Nx个货架，每个货架有Ny列、Nz层，所有货位长、宽、高均相等长度均为L，用Vy、Vz表示堆垛机在y轴和z轴方向上的运行速度，同时不考虑模型中堆垛机的加减速和启停特性，并约定每个货位只能存放一种物品，且一个入库托盘被视为一个入库订单，即将入库物料以入库托盘为单位重新划分入库订单。因为立体仓库存储部分与物料中转处理环节分离，所以不考虑不同货架间的距离。为了建立立体仓库模型，使用表1中的符号及其定义。

表1 立体仓库模型的符号定义与描述

立体仓库货位分配问题中常见的优化原则是 “效率优先原则”和“货架稳定性原则”，但在金属工业环境下堆垛机的负载均衡也尤为重要。依照立体仓库平稳、安全运行的要求和S公司实际需求，下面构建考虑立体仓库出库效率、货架稳定性及堆垛机负载均衡需求的多目标优化模型。

(1)效率优先原则

固定货架的立体仓库中，提升作业效率的有效方法是减少货物在堆垛机上的处理时间，即将货物放置于距离出入库平台更近的货位。在堆垛机能够在y轴与z轴同时运动的情况下，从货位(x,y,z)到达出入库平台原点(0,0,0)所花费的时间

(1)

根据效率优先原则，出入库频次高的货物需要放置在离出入库平台较近的货位上，以此减少仓库中出入库操作的时间，实现作业效率最大化。为了实现仓库效率最大化，构建了效率最大化货位分配目标函数，如式(2)所示：

(2)

式中Pi≠0。

(2)货架稳定性原则

货架稳定性原则主要考虑立体仓库在使用过程货架的稳定性需求。货架的稳定性和货架内仓储货物的分布有关，货物分布越集中在货架的低层，货架的稳定性越强，因此要保证货架的稳定性就要遵循“下重上轻”原则。受此启发，本文设计了货架稳定性货位分配优化目标函数,如式(3)所示：

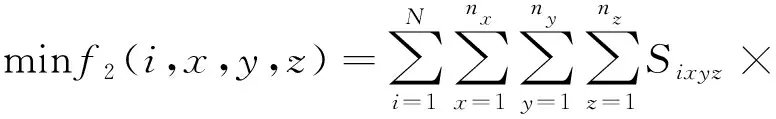
(3)

(3)堆垛机负载均衡原则

堆垛机负载均衡原则主要为了均衡每个过道内的出入库任务数量，避免托盘在一个巷道内堆积、堆垛机超负荷工作而影响作业效率及堆垛机寿命。同时，对于大中型立体仓库而言，货物分散在不同货架更有利于仓库运作。项前等[24]设计了以货架中占用货位数量的标准差来反映作业的均衡程度的堆垛机负载均衡目标函数，但仍难以完全反映不同过道的负载情况。本文对其设计的优化函数进行了改进，改进后的堆垛机负载均衡函数如式(4)～式(8)所示：

(4)

(5)

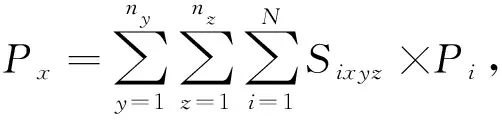
(6)

(7)

(8)

改进后的堆垛机负载均衡优化目标函数，不但考虑了货架中货物的数量均衡，而且考虑了货架中物料出入库频率的均衡，能够更加全面地反映货架的出入库负载差异。同时，该优化函数有利于物料的分散，避免物料频率分布不均造成的巷道堵塞或者堆垛机损耗不均衡的问题。

(4)约束条件

优化过程中，参数需要满足立体仓库的约束条件，避免出现不合法的优化结果。根据仓库配置参数和货位分配原则，对上述目标函数中的变量作了一些约束。具体约束条件如式(9)和式(10)所示：

(9)

(10)

以上约束条件保证了货位变量不会超出仓库配置，且保证货位与货物一一对应的关系，不会出现一对多的情况。式(9)表示每个入库托盘订单只能放在一个货位，而式(10)则要求每个任意货位只能存放一个入库托盘订单。同时，在整个货位优化过程中，约定入库订单托盘的数量不会超过可用货位的数量，即N小于等于当前仓库空闲货位数量。

为简化模型的求解，采用权重系数变化法对多个优化目标进行线性化。该方法将不同优化目标赋予不同的权重wj，最终优化目标表示为不同优化目标的线性加权。权重系数法求解多目标优化的描述如式(11)所示：

s.t.

(11)

通过分析S公司对立体仓库运作过程中的需求，利用层次分析法获得不同优化目标的权重。最终的立体仓库货位分配模型利用权重均衡了3个优化目标，实现了不同优化目标的均衡。所建立的立体仓库优化模型如式(12)～式(15)所示：

minf(i,x,y,z,nx)=ω1×f1(i,x,y,z)+ω2×
f2(i,x,y,z)+ω3×f3(x,nx),

(12)

(13)

s.t.

(14)

(15)

多目标进行线性加权时，为了消除不同目标量纲的影响，本文对以上3个优化目标函数均进行归一化处理。考虑归一化处理过程中可能出现数值溢出现象，将各个目标函数值归一化的公式如式(16)所示：

(16)

在对多目标进行线性化前需要确定各个目标函数的极值范围。由于大型立体仓库货位优化问题很难获取问题的精确解，本研究通过单目标优化实验获得各个优化目标的极值。同时，为了增加实验获取各目标函数极值范围的鲁棒性，对实验获得的最大值进行放大，最小值进行缩小。

2 基于遗传算法和延迟接受爬山算法的混合算法

本研究提出一种基于GA和LAHC算法的两阶段混合算法求解建立的立体仓库货位分配优化模型。为了集成GA算法的收敛能力和LAHC算法的局部搜索能力，混合算法分成GA和LAHC两个阶段，以最大化两种算法的寻优效率。GA阶段，利用遗传算法优秀的收敛能力，快速获得一个相对较好的初始解。然后，利用LAHC算法在上述初始解的邻域中搜索获得最优解。根据GA和LAHC算法的流程，本研究设计的两阶段混合算法的伪代码如下：

算法1GA-LAHC算法。

输入：种群大小Pn、最大迭代次数Maxgen、变异概率Pm、交叉概率Pc；初始化历史列表大小H和最大迭代次数maxiter;

输出：找到的最优解。

/* ---------------GA阶段 ----------------*/

初始化种群

gen← 0

Repeat: %重复

计算种群中个体的适应度值，并对种群进行联赛选择

随机选择一个个体替换为全局最优解

初始化一个空的新种群,Newpop

i← 0

Repeat： %重复

if Random(0,1)>Pcthen

随机从种群中选择两个个体,E1,E2

C1,C2←Crossover(E1,E2)

C1,C2←Repair(C1,C2)

end

if Random(0,1)>Pmthen

随机选择一个个体,E3

C3←Mutation(E3)

end

将子代添加到新种群中,更新Newpop

i←i+ 1

untili≥Pn

gen←gen+ 1

untilgen≥Maxgen

/* --------------- LAHC阶段 ----------------*/

短码转换为长码，并将转换后的长码作为初始解X

计算初始解的目标函数值f(X)

X*←X

f(X*) ←f(X)

初始化历史目标值列表，Lh←f(X),∀h∈{1,2,…,H-1,H}

j← 0

nidle← 0

Repeat： %重复

生产一个邻域解Y,并计算目标函数值f(Y)

iff(Y) ≥f(X) then

nidle←nidle+ 1

else

nidle← 0

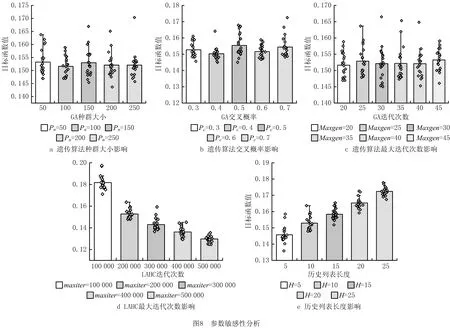
end

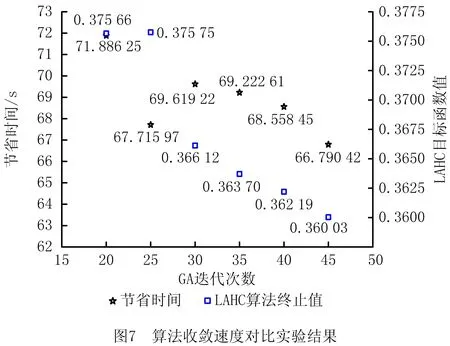
iff(Y)

X*←Y,f(X*) ←f(Y)

end

h← 1 +jmodH%取余

iff(Y)

X←Y,f(X) ←f(Y)

end

iff(Y)

更新历史列表，Lh←f(Y)

end

j←j+ 1

untilj≥maxiterornidle≥0.02 *maxiter

终止算法输出最优解

2.1 问题编码

求解离散问题整数序列编码方法被大量应用，如旅行商问题、车间调度问题、货位分配问题等。求解货位分配问题存在多种整数序列编码方式。在混合算法中采用了其中两种编码方法，如图2所示。两种编码在使用前均需对入库托盘订单和仓库货位进行整数编码。基于入库订单的整数序列编码是以入库订单数作为编码长度，为每一个入库托盘订单分配一个货位编号。基于托盘订单的编码能够减少编码的长度，在大规模问题上能够有效提升算法的效率，但不利于算法的全局探索。而基于货位的编码是以可用货位数量作为编码长度，将入库订单分配给不同的货位。基于可用货位的编码方式，有利于算法全局搜索，但是需要添加大量的哑订单，增加了算法的解码复杂度。

为了进一步利用两种编码的长处，在混合算法中同时利用了这两种编码方法，即两阶段编码。GA阶段采用基于入库订单的编码方法，利用遗传算法种群的优势来弥补编码全局搜索能力的不足；LAHC阶段则采用基于可用货位的编码方式，以充分发挥延迟接受爬山算法的局部搜索能力。因此，算法中存在问题编码的转换过程，编码转换过程如图3所示。编码转换的过程中需要使用哑订单占据多余的货位，其中哑订单的编号约定为0。

2.2 GA阶段

遗传算法是模拟达尔文生物进化论和生物遗传机理的生物进化计算模型，是一种模拟自然进化过程的智能优化算法。遗传算法的操作包含了生物进化的必须条件繁殖(交叉、变异)和生存(选择)。交叉过程中两个个体在基因层面发生交换，产生两个子代个体。常见的遗传交叉操作分为单点交叉(Single Point Crossover, SPX)和多点交叉。值得注意的是，离散优化问题双亲交叉操作容易产生非法解，这需要设计相应的染色体修复规则以修复非法解。GA阶段解的修复规则是将重复的货位编码随机替换为可行货位编码，子代通过选择机制决定自身基因传递的可能性。GA-LAHC算法的选择机制是精英保留和锦标赛选择机制，而变异操作则针对单个个体进行，个体有一定的概率能够提升自身的适应值(生存概率)。遗传算法中变异方式主要有单点变异和多点变异。GA-LAHC算法的变异采用了单点变异(引入新货位编号)和两点变异(交换货位编号)。在大规模立体仓库货位分配问题中，一次变异带来的效用极其有限。因此，GA-LAHC算法GA阶段的重点在交叉操作。事实上，GA-LAHC算法GA阶段的目的是为LAHC算法提供初始解。

为了最大程度地利用遗传算法的搜索能力，在最短时间内为延迟接受爬山算法提供尽可能优异的初始解，需要对遗传算法的交叉、变异操作进行改进。因为GA阶段的主要目的是快速获得一个相对优异的解，所以改进的重点不在变异操作中。而遗传算法出色的收敛能力主要来源于交叉操作，设计一种高效的交叉算子有利于算法的快速收敛。同时常规的双亲交叉只利用了个体层面的信息，而忽略了双亲个体基因层面信息的利用。受到BENNACEUR等[25]贪婪交叉算子的启发，本文设计了一种基于货位贪婪的交叉算子(Position Greedy Crossover, PGX)，以提升遗传算法的收敛和信息利用能力。

2.2.1 货位贪婪交叉

货位贪婪交叉算子在交叉过程中会利用个体中的每个基因信息，并对占优基因进行贪婪遗传操作。但这样处理会导致优势货位的大量重复，不利于算法的全局探索和货架间负载均衡，如图4中的子代存在多个9号货位(占优基因)。为了保证仓库内各个堆垛机的负载相对均衡和保留弱化优势基因，对货位贪婪进行限制。限制条件与货架储货状态有关，其定义如式(17)所示：

(17)

式中：SCx表示货架x的竞争力；¯P、Px分别表示仓库所有货架货物出入库频率的均值和x货架内出入库频率总和；Ox表示为x货架内存储货物的总数。货位贪婪的交叉算子具体过程如图4所示。

进行PGX交叉时，从种群中随机选取两个个体作为父代，同一个入库订单在满足货架竞争条件下进行货位编号贪婪交叉。货位交叉过程，货位分配会在货架竞争规则下向货位使用量少、货架内货物出入库频率低的货架倾斜。交叉过程中，在满足货位竞争通过计算父代中两个货位在当前订单的竞争值大小做出货位决策。交叉过程的表达式如式(18)所示：

(18)

式中:Li表示子代入库托盘订单i选定的货位编号;l1、l2分别表示父代个体1入库托盘订单基因i的货位编号和父代个体2入库托盘订单基因i的货位编号;ly、lz分别表示货位y轴和z轴上的值。通过货位贪婪交叉算子能够赋予遗传算法更快速收敛的能力。同时，由于货位贪婪交叉算子强化了遗传算法对基因层面信息的利用，遗传算法的优化能力也得到了提升。

2.3 LAHC阶段

应用PGX交叉的遗传算法虽然提升了收敛速度和对基因信息的利用率。但PGX交叉算子的引入不能改变遗传算法在大规模问题上容易陷入局部最优解的特性。遗传算法交叉的本质是旧解的拆解和个体旧基因重构。这种大范围的调整不利于算法的局部搜索，且容易产生大量重复搜索。虽然遗传算法存在变异机制，但由于交叉操作的进行，变异操作的效果将大大减弱。考虑到遗传算法局部搜索能力的缺陷，引入一种强有效的局部搜索机制就显得十分重要。延迟接受爬山算法作为一种迭代局部搜索算法，具有很强的局部探索能力。此外，该算法利用目标值作为当前解的跳跃约束，同时延迟接受爬山算法引入历史列表(搜索值列表)，极大地增加了当前解跳跃的灵活度，减小了跳出当前解的难度。

(1)初始化

LAHC算法的初始解是从GA中获得，将GA算法当前全局最优解编码转换成长编码形式作为LAHC算法的初始解。

(2)邻域生成

LAHC算法是一种邻域搜索算法，需要对算法的邻域探索方法进行约定。邻域搜索算子与遗传算法中的两点变异方法相似，在搜索过程中直接交换染色体内两基因的值，实现一次邻域搜索。由于解的结构中含有大量的哑订单，即虚拟的占位订单，为了减少无谓邻域搜索，本文对邻域搜索的起点作了约束，即在换位条件中约定交换基因值的两点中至少有一个基因位置的基因值不为0。

3 仿真数据案例分析与实验

3.1 实验平台

仿真实验在Pycharm环境中进行，使用的计算机硬件配置为Intel Core @i5-8 300H 2.3 GHz，16 G RAM；仿真实验中立体仓库各个参数如表2所示。

表2 立体仓库参数表

本研究的优化入库订单中包含498种商品，2 302个入库托盘订单，需将这些入库托盘订单在上述的5 040个货位的立体仓库中进行货位分配优化。入库托盘信息包括物料编号、出入库频次、质量等。

3.2 实验与结果分析

根据层次分析法，将目标1～目标3分配的权重分别设置为0.388 8、0.277 7和0.333 5。进行仿真案例优化实验前，需要对所建立模型的有效性进行验证，以保证优化结果的可靠性。模型验证完成后，对混合算法进行有效性验证实验及参数敏感性分析实验。

3.2.1 模型验证实验

根据SARGENT等[26]阐述的模型验证和检验方法，模型验证采用案例验证法。模型验证实验使用一个小规模案例在IBM公司开发Cplex软件中进行求解验证。验证案例包含4个货架，每个货架有6列5层30个货位。案例需为35个入库托盘订单分配仓储货位。入库订单信息如表3所示。

表3 模型验证案例待分配订单信息

Cplex软件的优化流程主要包括3个步骤：定义变量和加载数据、明确优化目标、添加约束。考虑到堆垛机均衡目标涉及到了多个货架的仓储数量及其订单物料的出入库频次，且优化目标公式较为复杂，直接添加该优化目标有一定难度。针对堆垛机负载均衡优化目标，在实际模型测验中将其转化成优化模型约束。出入库效率和货架稳定性的优化目标则参考Cplex多目标建模指导文件，进行配置两个优化目标的属性。

为了检验Cplex优化结果的质量，利用延迟接受爬山算法进行优化对比实验。LAHC算法最大迭代次数设置为10 000 000，历史列表长度设置为50。LAHC算法优化结果与Cplex求解结果对比如表4所示。针对同一入库订单的分配比较了货位出入时间和货位重心，将各自优势货位进行加粗显示，相应的订单编号带*号。加粗显示的货位表明该货位至少在一个优化目标上优于另一种分配方案。结果表明Cplex模型解在23个货位分配优于LAHC所得最优解。Cplex模型求解结果也印证了模型能够求解，且求解结果优于LAHC算法。

表4 模型验证结果对比

3.2.2 算法验证与分析

在混合算法有效性验证实验中，对比了单点交叉遗传算法(GA-SPX)、改进遗传算法(GA-PGX)、LAHC算法及改进粒子群优化(Improved Particle Swarm Optimization, IPSO)算法。IPSO算法流程和参数可参考文献[17]，实验中算法最大迭代次数统一为300次。GA算法种群设置Pn=100,Maxgen=300,Pc=0.6，Pm=0.95。算法的基准设置为进行20次随机存储策略(Random Storage Policy,RSP)所得的平均值。算法有效性验证实验重复进行了20次，实验所得结果如表5所示。

表5 算法有效性验证实验结果

根据表5的数据，GA-LAHC混合算法在求解精度和稳定性上远优于GA-SPX和GA-PGX。GA-LAHC算法的求解质量较RSP和GA-PGX分别提升了80%和50%以上。与LAHC相比，GA-LAHC算法在稳定性和求解质量上都有所提升，其中求解质量提升相对较大。GA-LAHC算法优化结果比LAHC算法提升了5%，少数情况下求解质量提升达13%；在算法稳定性上，GA-LAHC算法的稳定性与LAHC相比，提升不大。GA-LAHC较GA-SPX在求解精度和稳定性上都有较大的提升。IPSO在求解结果上稍优于GA-SPX，但求解稳定性远优于GA-SPX。这是因为IPSO针对集装箱货位优化改进的策略不适应立体仓库货位优化场景。相对其他算法来说，IPSO在求解稳定性上具有一定的优势。

为了更加直观地展现这几种算法的性能，对以上几种算法的收敛过程进行了可视化，结果如图5和图6所示。根据图5和图6可知，IPSO表现与GA-SPX相差不大，但是IPSO搜索最优解的能力优于GA-SPX。这是因为IPSO利用了新的拓扑结构来引导粒子跳出局部最优解。但由于案例和解编码的调整，IPSO算法的性能无法完全释放。根据“No Free Lunch”定理可以推断，如果对IPSO进行针对性改进，IPSO也能取得相对较好的优化效果。

就LAHC算法而言，由图5可以看出LAHC算法在求解货位分配问题上的求解质量不劣于GA-LAHC算法。LHAC算法优化结果在RSP存储策略的基础上提升了79%，优化性能略逊色于GA-LAHC。从实验结果上看，LAHC算法能够解决立体仓库货位分配问题。但观察LAHC算法的收敛曲线不难发现，LAHC算法存在收敛较慢的缺点。结合图5和图6的收敛曲线，可以发现GA-PGX算法收敛速度优于其他算法(GA-LAHC除外)。此外，算法收敛曲线可以验证GA-LAHC算法很好地融合了GA和LAHC算法的优点。

由图5不难观察到，GA-LAHC算法在GA阶段的收敛速度要快于LAHC算法。为了定量分析GA-LAHC算法与LAHC算法在GA阶段的收敛速度，设计了收敛速度对比实验。收敛速度对比实验中，LAHC的终止条件设定为运行20次GA算法所得最优目标函数值的均值。记录GA算法和LAHC算法所用的CPU时间，将LAHC算法所耗时间与GA算法CPU时间的差作为节省时间。为避免出现偶然性，LAHC算法也进行20次。算法收敛速度对比实验结果如表6和图7所示。分析表6的数据可得，GA-PGX算法增加迭代次数与节约时间收益成反比，且随着迭代次数增加，节约时间收益加速减少。这是因为PGX交叉算子加强了对个体基因信息的利用，强势基因的支配地位很难出现松动。然而，混合算法GA阶段的任务是获得较好的初始解。根据GA的收敛曲线可知，盲目增加GA算法的最大迭代次数只会浪费大量的计算资源，而初始解的质量没有明显提升。LAHC算法优异的邻域搜索能力，配合历史列表中以目标函数值为导向的超平面能够快速地跳出局部最优解，极大地改善了GA局部搜索能力弱的问题。根据图7的结果，合理设置GA的迭代次数能够加速GA-LAHC算法的收敛。

表6 算法收敛速度对比结果

3.2.3 算法参数敏感性实验

GA-LAHC算法融合了GA和LAHC算法，参数选择也变得更加复杂。为了更好地确定GA-LAHC算法的参数，本文对算法的参数进行敏感性分析，以确定最佳的参数组合。本文提出的混合算法在GA阶段的目的是生成一个较好的初始解。因此，GA阶段不考虑遗传算法变异概率对算法局部搜索能力的影响。根据前文对算法的描述，对混合算法的中GA种群大小Pn、GA交叉概率Pc、GA最大迭代次数Maxgen、历史列表长度H和LAHC算法最大迭代次数maxiter进行敏感性分析。参数敏感性分析实验分别进行20次，如表7所示为参数敏感性分析的统计结果。同时，为了更加直观地展现各个参数对算法的影响，将所有实验结果以散点柱形图的形式呈现，结果如图8所示。

表7 GA-LAHC算法参数敏感性实验

从图8不难发现，GA参数对GA-LAHC算法的稳定性影响较大，而对算法求解精度影响较小。由图8a和表7可知，GA种群规模增大到一定程度上可以提升算法求解稳定性。GA阶段种群规模对应GA的搜索空间大小。增加GA种群规模意味着扩大搜索空间，GA获得解的多样性就会增加。这导致了种群规模增加混合算法获得解的离群值恶化，而解的聚集度增加的现象。考虑计算时间和算法稳定性的均衡，最佳的种群数量应定为100。其次，GA阶段的交叉概率影响了GA算法的全局探索能力，对LAHC阶段初始解的质量有较大影响。就Pc的数值而言，Pc值越小交叉的概率就越大，种群内进行的交叉次数就越多。结合图9中不同交叉概率的GA-PGX收敛特性可以发现，当Pc超过一定阈值时GA-PGX在小迭代次数下目标函数值没有显著提升。结合图8b和图9可以推测阈值在0.4～0.7之间。为了保证算法的稳定性和求解速度，本文设定的最佳交叉概率为0.6。根据图7和图8c所示的结果，两个实验都证明了在迭代次数满足GA获得较好初始解的前提下，增加GA算法的迭代次数对算法求解质量的影响很小。综上可知，本文提出的GA-LAHC算法在GA阶段的最佳参数组合为：Pn= 100;Pc= 0.6;Maxgen= 20。

LAHC算法的参数较少，主要有历史列表长度H和最大迭代次数maxiter。历史列表存放了LAHC算法搜索过的目标函数值，限制了LAHC算法可接受邻域解的范围。在相同的条件下，历史列表长度越大，LAHC可接受邻域就越丰富，邻域生成难度越小，具有更强的局部探索能力。同时，历史列表长度约束了搜索步长，搜索步长越小，探索难度越低，求解稳定性就越高。图8e定性地验证了，H越大搜索效率越低。但需要注意的是过小的H会使得算法邻域搜索难度过大，导致算法极易陷入局部最优，且难以通过简单邻域跳出局部最优解。当H=1时，LAHC退化成完全随机搜索算法。而maxiter决定了LAHC算法探索邻域的最大次数，探索次数增加能够获得更优解的概率也增加，图8d也验证了这个结论。观察图8d可以发现，随着迭代次数的增加求解质量的提升幅度在减少。根据对LAHC参数敏感分析的结论，考虑到算法的优化成本，本文设H=5，maxiter=250 000。

GA-LAHC算法能够求解立体仓库货位分配问题，这是因为算法集成了GA的全局探索能力和LAHC的邻域搜索能力。混合算法最优解的提升依赖LAHC算法。LAHC算法核心在于其利用目标函数值为导向的变邻域局部搜索方式。当前解通过邻域生成算子试探比当前解更优或历史记录更优的邻域结构，产生更好的邻域解。历史列表一方面用来记录算法搜索历史；另一方面其作为当前解转换结构的约束条件，限制了可接受的邻域结构，引导算法向更优的目标值探索。LAHC算法的搜索方式能够求取最优解的前提是当前解能够通过一系列邻域结构转换成最优解的结构，即要满足更优解是较优解的邻域之一的条件。GA-LAHC算法和LAHC算法在货位分配问题上取得较好的优化结果，也从侧面印证了货位分配问题满足LAHC算法的前提条件。但对比模型验证和算法验证求解效果可以发现，在不同问题规模小货位分配问题解空间的连续性有一定的差异。小规模问题上，以目标函数值为导向解空间连续性不足，导致简单的邻域生成方式难以获得较满意的优化结果。LAHC算法的缺点在于单点探索方式效率较低，这也是LAHC算法前期收敛速度不如GA的主要原因。而GA-LAHC算法利用了GA的全局探索能力来解决LAHC前期收敛速度较慢的问题，为LAHC局部搜索提供较好的初始解。总的来说，GA-LAHC算法结合了GA和LAHC算法的优点，同时也能够有效地优化求解立体仓库货位分配问题。

4 结束语

本研究在立体仓库货位优化的常见原则的基础上，考虑堆垛机的负载均衡，设计了包含出入库效率、货架稳定性和堆垛机负载均衡的多目标优化模型，并提出一种基于改进GA和LAHC算法的两阶段混合算法。该算法解决了LAHC算法收敛速度较慢和GA局部搜索能力弱的问题，同时提升了算法的求解稳定性和精度。GA-LAHC算法较好地集成了GA算法和LAHC算法的优点。在一个5 040货位的仿真案例中，GA-LAHC算法的最优解比GA-PGX和RSP分别提升了56%和80%。在求解精度上，GA-LAHC比LAHC算法求解结果提升了5.9%，可以有效求解立体仓库货位分配问题。同时，对比IPSO算法的求解结果，GA-LAHC在求解精度上有明显优势，但在求解稳定性上差距不是很大。总的来说，GA-LAHC算法能够求解所建立的立体仓库货位优化模型，并取得相对较好的优化结果。

尽管所提出GA-LAHC算法的有效性得到了初步验证，但与实际应用需求仍有一定的差距，同时所采用的邻域搜索算子还过于简单，没有充分利用领域知识。在后续研究中可以增加约束和优化目标，以更加接近实际情况；其次，利用领域知识设计更加高效复杂的邻域搜索算子，提高算法在不同问题规模的适应性，提升算法的实效性。