生育政策、人口流动对宏观经济的影响

郑录军，韩庆潇

（中国人民银行济南分行，山东 济南 250021）

随着生育率的不断降低以及人口预期寿命延长，全球不可逆转地进入老龄化社会，并对各国消费、储蓄、投资、经济增长以及金融环境产生深刻影响。中国从计划生育政策实施以来，生育率不断下降，导致老龄化速度前所未有。正是为了应对老龄化问题，十八届三中全会提出了启动“单独二孩”政策，两年后的十八届五中全会决定实施“全面二孩”，2021年则再次放开“三孩”政策，计划生育政策调整进一步加快。在中国特殊的国情下，生育率持续下降主要受强制约束的生育政策影响，因此，生育政策的放松必将对中国人口规模和结构的走势产生重要影响。与此同时，各地区为了改善人口结构，主动出台优惠政策，在市场自愿机制下，积极引导优质人力资源流入。尤其是2020 年以来，武汉、杭州、成都等几十个热点城市纷纷出台人才新政，掀起了一场“抢人大战”。与过去农民进城为主的区域内纵向流动方式不同，本次人口迁移主要表现为年轻劳动力的横向跨区域流动，可能带来全国人力资源的区域间再分配。如果说生育政策调整带来了人口走势时间维度的变化，那么跨区域人口流动则改变了人口的空间分布，二者叠加导致的人口时空变化将对中国宏观经济产生更加复杂的冲击。当前，人口变化在产出方面的积极作用尚不明显，却明显提升了居民的购房需求，带来了房价上涨和居民负债增加的压力；人口跨区域流动虽然为部分地区经济增长带来活力，却使落后地区成为了人才流出的重灾区。因此，从更广泛的视角来看，人口数量和结构的时空变动将对人力资源分配、区域经济发展和金融环境带来一系列深层影响。然而，以上人口因素到底会对经济增长产生何种程度的影响？又会带来怎样的风险冲击？这两个维度的人口调整方式有何内在差异？在长短期有什么不同影响？这些问题值得深入研究。

1 文献综述

从人口角度探索经济增长问题由来已久，早在1958年Samuelson［1］就开创了世代交叠模型（OLG），分析了代际转移对财富储藏和经济增长的作用。而后Diamond［2］对模型进一步完善和拓展，形成了较为成熟的二期OLG 模型，通过区分年轻人和老年人引入年龄结构异质性的影响，为理论研究创造了规范的模型范式。自此，从人口角度探索经济增长的研究日益丰富，特别是随着老龄化问题的加剧，人口老龄化对经济的影响成为国外学者们探讨的焦点，但却并未达成一致观点。目前，大部分学者证实了老龄化对经济的负面影响［3-5］，主要基于OLG 模型对本国人口和经济情况进行了模拟，认为生育率下降导致劳动适龄人口比例逐步下降，进而减少了劳动力供给和储蓄水平，抑制经济产出增长。但也有少数学者得出了相反的结论，如Futagami 等［6］的内生增长模型显示，存在寿命延长的条件下，人口老龄化的负面效应将会削弱，经济产出可能收敛于更高水平。此外，还有学者认为人口老龄化对经济的影响存在不确定性，如Zhang 等［7］通过建立三期的OLG 模型证明，人口老龄化对经济增长的影响因国家而异，人口老龄化对发展中国家的经济增长会产生显著的正面影响，但会显著抑制发达国家的经济增长。

近年来，人口老龄化问题也成为中国必须面对的严峻挑战，但与国外研究方向不同，国内更加关注应对老龄化的手段。因此，相关研究主要集中在生育政策与人口流动方面，且在研究方法主要采用了实证检验，而较少运用OLG 模型。在生育政策方面，部分学者肯定了生育政策调整对经济的正面作用，如陆旸等［8］实证检验结论显示，放开计划生育政策有利于减缓潜在增长率的递减趋势；汪伟［9］则通过建立三期OLG 模型的数值模拟发现，生育率与经济增长的关系呈现“倒U 形”，因此放开计划生育政策后，如果生育率不出现大幅度反弹，将有利于经济增长；魏丽莹［10］构建了消费者、生产者和政府三个部门的多区域OLG‑CGE 模型，通过模拟发现全面二孩政策有助于京津冀地区GDP 增长。但是，黄少安等［11］则认为放松计划生育政策会导致中国陷入“人口红利”依赖症，无法实现从人口结构优势向产业、人力资本与技术升级优势转化，不利于长期经济增长；刘晓曦等［12］基于三阶段划分的OLG 模型模拟发现，全面二孩政策下人口增长率提升可以增强房地产行业对经济的影响力，但同时也会挤占其他行业投资，从而抑制整体经济发展。在人口跨区域流动方面，阮荣平等［13］基于人口流动省级面板数据的实证研究表明，人口流动总体上削弱了输出地的人力资本积累。侯燕飞等［14］利用2005—2014 年29 个省份面板数据进行实证检验证明，人口净流入促进了区域经济增长。郭东杰等［15］利用省际面板数据研究了抚养水平、人口变迁和居民消费之间的关系，发现跨地区人口流动扩大了整个居民部门的消费水平，但是对于人口流出地区却是不利的；孙继国等［16］基于省际面板数据的实证检验发现，人口流动会通过调节居民工资水平进而对地区经济增长产生影响，且西部地区人口流入的经济效应更加明显；龚锋等［17］基于人口普查的县级数据的实证检验发现，人口流入有助于缓解人口老龄化对经济增长的不利冲击。

此外，在人口因素影响经济增长的同时，带来的金融波动风险也逐渐引起关注。如陈雨露等［18］基于119 个国家（地区）的实证研究表明，人口老龄化与金融杠杆呈现显著的倒U 型关系，且在越过老龄化“拐点”后，“去杠杆化”进程将随金融危机发生概率而明显上升。Lisack等［19］基于多期OLG 模型的研究表明，生育率和死亡率同时下降，导致房地产价格和居民负债水平上涨。蒲火元等［20］基于广州数据的实证检验表明，中心城市大量人口流入引致城市房价上涨，进而推升了居民买房的负债水平。杨华磊等［21］通过动态优化模型的模拟发现，受人口老龄化影响，中国将在2050 年前步入资本收益的下行通道，从而导致资本外流的金融风险明显加大。

通过梳理以上文献可知，目前国内OLG 模型的构建仍相对简单，鲜有能够纳入动态一般均衡分析框架进行深入分析的研究，导致生育政策调整对经济影响的内在机理尚不清晰。究其原因，一方面，OLG 模型纳入动态一般均衡分析框架较为复杂，区分年龄结构异质性会使居民部门行为方程数量翻倍，对模型稳态和冲击模拟带来巨大挑战；另一方面，国内外经济情况差异巨大，无法直接套用国外模型，如在人口生育率方面，国外生育率的改变是内生调整，而国内生育率变化却受生育政策外生影响，二者机制完全不同。基于此，为了能够准确分析人口因素对中国经济增长和杠杆率的影响，该研究在OLG 模型标准范式基础上，进行了相应的调整和改进，使之贴近中国的现实情况，能够清晰展示宏观变量调整的内在机理；然后，结合人口方面的经验数据，对全国和地区经济增长和风险冲击进行了初步判断，增强了文章结论的实践价值。因此，该研究试图在以下方面有所贡献：第一，将生存率、劳动效率、房产购买和遗产倾向等重要的年龄异质性因素纳入OLG 模型，探索适合国内研究的分析框架；第二，拓宽研究视角，从人口时空变动的角度出发，分析生育政策调整和人口流动带来的经济效应和风险冲击，展示更加清晰的内在机理；第三，结合当前的经验数据，对全国和地区的人口影响进行初步判断和预测，为经济决策提供更加合理参照标准。

2 理论模型

为全面分析人口因素的影响，该研究将OLG 模型（世代交叠模型）纳入动态一般均衡的分析范式，在充分考虑不同年龄人口异质性的基础上，构建符合国内实际情况的理论模型，通过模拟生育政策调整和人口流动对宏观经济的影响过程，更加清晰地揭示人口时空变化冲击的内在机理。

首先建立在封闭经济中包括居民、企业、商业银行和政府的四部门动态一般均衡模型。根据中国人口生育率变化的现实情况，假设在长时间的独生子女政策背景下经济逐步实现稳态增长，而随着年轻人生育观念的改变及生育政策的调整对稳态产生新的冲击，在完美预期的条件下，经济增长等宏观变量在波动中向新的稳态过渡。此外，考虑到人口规模调整时间跨度较大，价格调整更加具有弹性，货币冲击也趋于中性，所以仅研究人口变化对实际变量的影响。

2.1 人口变化情况

该研究模拟国内人口就业、退休和寿命情况，建立八期的生命周期模型，年龄从7 岁到86 岁，每期代表10 年。这一建模方式较两期的OLG 模型能更加全面地反映现实情况，且比每年一期的建模方式更加简洁和明确。为反映代际更迭的情况，将居民儿童期设定为第0 期（7～16岁），此期并不具备独立行为能力，消费支出完全依赖于父母；第5 期（57～66 岁）部分人口开始退休并获得养老金。人口增长的公式为：

其中：P代表人口规模，ρ代表生育率，φ代表跨期生存率；而上标j代表年龄期（包括0～7 期），其中0 为儿童期，1 为成年后第1 期，t则代表当期时间。与生命周期相同，时间t的变化同样为10 年一期。因此，区别于传统一般均衡模型，该研究时间变动代表年龄期j与时间t的同时增长。需要注意的是，OLG 模型假定人口生育仅集中在第1 年龄期，因此公式（1）表示人口生育过程，而公式（2）表示人口年龄增长过程中的生存情况，即医疗水平的表现。基于此，人口总规模的计算公式为：

公式（3）中Pt代表t期成年人的总规模，而公式（4）中PAt代表全部人口总规模。

2.2 居民部门

假定处于第1 年龄期的代表性居民通过选择各年龄期的消费、养孩支出、劳动供给、房产购买和净储蓄水平来实现效用最大化。其总体效用函数如下：

公式中，β为居民效用的折现因子，而U代表每一年龄的效用函数，具体形式如下：

公式（6）表示年龄期为1～6的效用函数，公式（7）则为第7 年龄期的效用函数。其中和分别为各年龄段居民消费需求、劳动供给和买房需求，相对应的和则为各年龄段居民对闲暇和买房的偏好参数。此外为养孩成本，χ1t则为第1 年龄期的养孩支出偏好，系数之前乘以(1 +ρt)则表示随着孩子数量增加，养孩偏好同比例上升，这一点与买房倾向类似。为第7 年龄期老人为后代留下的储蓄，ψ表示遗产倾向。每个居民面临的预算约束条件为：

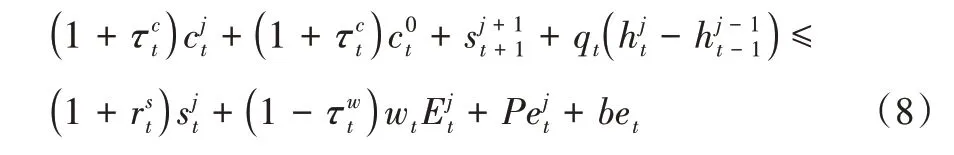
等式左右两边分别表示居民各年龄段的支出和收入。其中：支出包括消费、养孩成本、净储蓄和房产购买；收入主要包括利息收入、工资收入、养老金和遗产收入。和分别表示消费税率和工资税率，qt为实际房地产价格为各年龄段净储蓄，并假设第1年龄期期初的净储蓄为0，后几期为负则是负债，为正则为储蓄。为人力资本，计算方式为代表各年龄段的劳动效率。此外，为养老金，只有达到退休年龄才可领取。bet为遗产收入，主要来自年龄期为7的老人遗留的储蓄和房产。

根据方程（5）、（6）、（7）、（8），求解最大化问题可以得到消费的欧拉方程、养孩成本、劳动供给、房地产需求公式：

需要注意的是，方程（12）中j'表示下一期增加房地产购买的年龄期，而并非每个年龄期都存在房地产购买意愿，这与现实情况一致。此外，根据第7 年龄期的效用函数和约束方程，得到房地产和储蓄遗产方程。

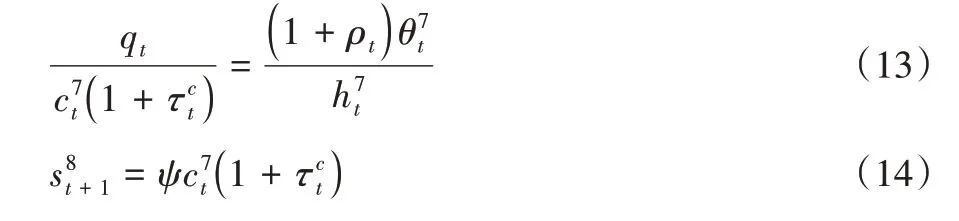
参考Sudo 等［22］的做法，模型假定遗产转移来自两个部分，一是各年龄期死亡人口的储蓄和房产，二是最后年龄期老人主动遗留的储蓄和房产。其中，房产按当期价格变卖后转移给后代。全部遗产平均分配给下期所有成年人口。因此，其计算公式为：

公式中，的值按照计算，表明第7 年龄期老人死亡后，储蓄和房产全部成为遗产。

2.3 厂商部门

假定在完全竞争市场环境下，厂商通过雇佣劳动力和贷款进行生产，其利润最大化的目标函数为：

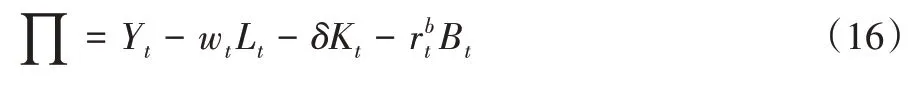
其中：Yt为厂商产出，Lt、Kt和Bt分别为劳动力、资本和贷款，wt、δ和rbt分别为工资、资本折旧率和贷款利率。厂商面临的约束条件包括：

公式（17）表明厂商服从规模报酬不变的Cobb‑Doug‑las生产函数。其中，At为全要素生产率，由于随机变化的技术冲击将导致模型转轨路径无法获得，因此，全要素生产率设定为1。公式（18）为厂商贷款约束方程，方程左侧为贷款本息和，右侧为资产价值Kt的贷款条件，其中m为贷款价值比。

根据方程（16）、（17）、（18），求解最大化问题可以得到工资和贷款利率的方程：

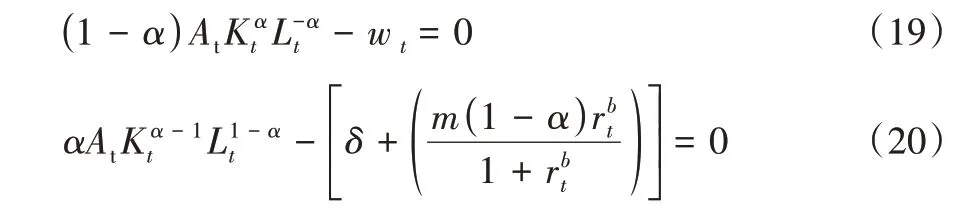
此外，根据资本积累过程，可以得到投资方程：

根据各年龄段人力资本水平，可以得到劳动力总供给水平为：

需要注意的是，第5年龄期的劳动供给水平需要扣除κ比例的退休人口。

2.4 银行部门

商业银行作为模型中唯一的金融机构，根据市场供求配置资金并调整利率水平，发挥着金融中介作用。为简化模型，假定银行部门从居民部门吸收存款，同时向企业放贷和购买政府债券，因此，银行面临资金和利润两个约束条件：

公式（23）为资金约束条件，表示银行从各年龄段居民吸收的储蓄总和St，其计算公式为，总储蓄除了上缴bt比率的存款准备金之外，用于向企业贷款Bt和购买政府债券Dt。公式（24）为利润约束条件，表示银行从企业贷款和政府债券中获得利润和，其中和为贷款利率和债券利率。而银行利润按照存款利率和利润率πb支付给居民和用于银行运营。考虑到政府债券风险较低，因此假定债券利率低于贷款利率且二者差值固定，公式为为二者之差。

2.5 政府部门

假设政府每期都能实现预算平衡，其预算约束方程为：

其中：g为政府购买占总产出的比重，d为政府债券占总产出的比重。

2.6 房地产市场出清条件

各年龄段居民房地产购买需求加总可以得到总的房地产需求方程：

在房地产供给方面，部分文献假设房地产供给增速与人口增速持平，保证人均房地产水平不变；也有文献将房地产供给水平假设为固定值［19，23］。这两种处理方式显然与国内现实情况差别较大。长时间以来，中国城镇土地供给不足，导致城镇人口增速超过房地产供给增速，特别是在部分人口吸引力较大的热点城市更为突出。因此，房地产的数量和价格应该对居民的资产和负债产生重要影响。基于此，根据人口数量与房地产供给的长期关系，将房地产供给方程设定为：

3 数值模拟

3.1 参数校准

考虑到1993 年前后中国经济结构的变化较大，且统计口径发生调整，因此该研究选择了1994—2003 年的数据进行校准，以2003 年为稳态的初期值，并基于2004—2013 年的数据对部分参数的数值进行了预测，模拟人口等相关变量的调整对宏观经济的影响。此外，由于模型一期跨度为10年，该研究参照Bouzahzah等［24］的方法进一步对部分参数进行了调整。相关参数校准的原始数据主要来自于《中国统计年鉴》《中国人口统计年鉴》《中国房地产统计年鉴》以及《中国家庭收入调查》等。

3.1.1 人口变化情况的相关参数

（1）人口年龄期划分。参照国内生育、就业、退休和死亡的情况，将年龄段划分为8 期，10 年为1 期，分别为7～16 岁、17～26 岁、27～36 岁、37～46 岁、47～56 岁、57～66 岁、67～76 岁、77～86 岁。需要特别说明的是，7～16岁为第0 年龄期，为了构建OLG 模型，仅以第0 期代表整个儿童期，且儿童无法独立参与经济活动，其消费水平取决于父母；17～26 岁为第1 年龄期，按照人口代际交叠的设定，仅本期可生育孩子；57～66 岁为第5 年龄期，本期部分人口开始退休，不再提供劳动力但领取养老金；77～86 岁为第7 年龄期，作为生命周期的最后一期，老人考虑在死亡之前留下部分遗产。

（2）生育率。在性别比例为1 的背景下，为了满足动态一般均衡模型稳态条件，已有文献普遍将生育水平设定为1［24-25］，即生育率ρ=0。但是，相比较国外稳定的生育率水平，国内同时受到生育意愿下降和生育政策调整正反两方面的影响，生育率变化幅度较大，内在机制也更加复杂。根据联合国公布的中国1994—2013年的总和生育率数据，2003年前后总和生育率变化较小，但这一数值并未达到模型稳态条件，因此将2003 年稳态期的生育水平调整为1（ρ=0）。而为了模拟生育观念变化和人口老龄化水平提高，文章将第1期生育水平设定为0.9（ρ1= -0.1），并结合人口预测的相关研究［26］，将2014—2023 年生育政策逐步调整后的生育率分为三种情景。第2—6期分别为低生育水平（1，1，1，1，1），代表较弱的政策效果，生育率仅能直接恢复稳态；中等生育水平（1.05，1.037 5，1.025，1.012 5，1）和高生育水平（1.1，1.075，1.05，1.025，1），表明政策效果较明显，生育率皆有大幅提升，而后逐步衰减至稳态生育率。因此，各期生育率(ρ1，ρ2，ρ3，ρ4，ρ5，ρ6)分别为低生育率（-0.1，0，0，0，0，0），中等生育率（-0.1，0.05，0.037 5，0.025，0.012 5，0），高生育率（-0.1，0.1，0.075，0.05，0.025，0）。

（3）生存率。参考第5次和第6次人口普查的数据，将各年龄期10年的人口生存率数据依次相乘得出相对应的生存率，然后根据两次人口普查数据的平均值得出2003年稳态时各年龄段生存率值。此外，根据已有文献，将儿童期生存率设定为1。因此，稳态时的各年龄段生存率（φ1，φ2，φ3，φ4，φ5，φ6）=（1，0.995，0.992，0.96，0.9，0.74）。

3.1.2 居民部门参数

参考Bouzahzah 等［24］的计算方法，文章将消费者跨期替代率β设定为0.84；根据Muto等［5］方法将闲暇偏好γ设定为1.5；孩子支出偏好χ 与文献［9］一致，设定为1；购房偏好系数θ的设定，则结合Lisack 等［19］的计算方法，假定居民仅在第1年龄期购买房产，根据历年房地产价值与总产出的关系，计算出第1 年龄期的购房偏好系数θ1为4。遗产倾向系数ψ的设定与国外文献不同，由于第7年龄期老人代表77～86 岁所有人口，而非仅86 岁末期老人的遗产倾向，且国内外收入和消费数据差别巨大，这就使得参数值变化较大。根据《中国家庭收入调查》这一年龄段的消费和储蓄情况，结合稳态公式将遗产倾向系数ψ设定为2。各年龄段劳动效率的计算根据《中国家庭收入调查》中居民各年龄段平均工资收入和工作时间情况，反推出各年龄段单位工资差异，然后以第1期为基准计算出各期劳动效率（ε1，ε2，ε3，ε4，ε5）=（1，1.39，1.4，1.3，0.98）。

3.1.3 厂商部门参数

参考许志伟等［27］的计算方法，计算得出资本折旧δ为0.4；根据历年GDP收入份额中劳动者报酬占比计算出资本份额占比α 为0.35；根据Gerali 等［28］的方法，结合历年工业企业贷款与资产的数据测算出贷款价值比m为0.35。

3.1.4 银行部门参数

根据中国人民银行存款准备金数据，存款准备金率设为0.2；参考杨熠等［29］的计算方法，根据上市银行历年财务报表，得出银行利率净收入占存款总额的比例πb为0.025；根据人民银行公布的一年期贷款基准利率与财政部公布的一年期国债收益率，计算得出10 年期贷款与债券回报差ζt为0.2。

3.1.5 政府部门参数

工资税率τw和消费税率τc参考吕冰洋等［30］的计算方法，根据历年数据分别计算为0.1 和0.13；第5 年龄期退休人口占比κ则根据中国退休年龄规定进行估算，但考虑到部分自由业者等可以灵活推迟退休年龄，因此将稳态期κ设定为0.7；政府购买占比g和政府债券占比d参考托雷斯等［31］的取值和计算方法，分别设定为0.14和0.03。

3.1.6 房地产供给相关系数

根据各年龄段生存率以及稳态出生率可以计算初期人口稳态值-P为6.33；根据第6次人口普查的人均住房面积和《中国房地产统计年鉴》中的历年商品住宅房屋竣工面积，可以计算出2003年人均住宅面积，进一步折算为人均住房数量0.31，因此，初期住房总量的稳态值-H为1.96；根据历年房地产供给和人口增长关系，可以计算出房地产增速系数η为0.68。

3.2 生育政策调整的模拟分析

根据文献［25］的建模和求解方法，可以将人口方面的因素设定为外生冲击，在计算人口结构动态调整过程的基础上，模拟冲击对经济的影响过程。因此，将生育政策调整导致的生育率变化作为外生冲击，以确定性模拟方法模拟经济从初始稳态向最终稳态过渡过程。首先，模拟生育政策调整对经济产出和储蓄的影响。结果显示，居民负债主要源于第1 年龄期（17～26 岁）购买房产和养孩支出增加，且第2 年龄期（27～36 岁）的收入仍然无法完全覆盖前期的负债，这说明在这两个年龄期的居民属于借款者；从第3 龄期（37～46 岁）开始居民储蓄才调整为正，从而转变为净储蓄者。这一结果最大程度地模拟了不同年龄结构下居民储蓄和负债的现实情况，也为计算居民杠杆率提供支持。由于该研究储蓄以期初值表示，因此，居民负债水平的计算方式为LEV h=P1s2+P2s3，进而得出居民杠杆率LRh=LEV h/Y。可以计算出企业杠杆率LRp=B/Y，政府杠杆率LRg=D/Y=d，全社会杠杆率LR=LRh+LRp+LRg。根据以上公式，从经济增长和杠杆率风险两个角度出发，模拟两个稳态之间的转轨路径，通过对比不同情景下的经济波动情况，探索生育政策调整的作用及其内在机理。

3.2.1 低生育率的政策效应

如前所述，在低生育率情景下，“二孩”“三孩”的政策作用较小，仅能抵消2003年以来生育意愿的下降，使生育率恢复稳态值。在这一假定下，宏观经济变量走势如图1所示。

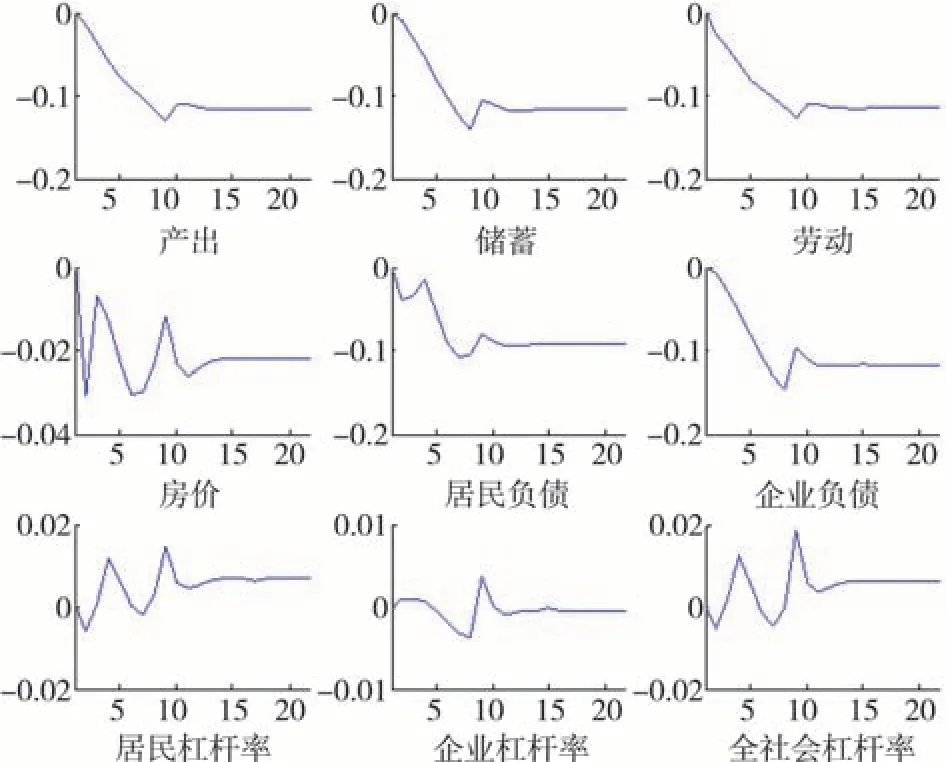
图1 低生育率的经济效应

从经济增长角度来看，初期生育率下降带来的经济下行压力短期内难以改善，导致产出水平延续下行趋势。但在新的生育政策支撑下，产出缓慢趋于新的稳态水平，而终值低于初期稳态值。根据模型的内在机理可知，由于生育政策调整的刺激作用较弱，短期内适龄劳动人口持续下滑，在此背景下，一方面劳动力供给水平难以提升，另一方面利率下滑的预期助推储蓄回落，导致资本积累水平的缓慢下降，二者共同作用于总产出。直到生育政策抑制住人口下滑趋势，劳动力供给和储蓄才趋于平稳，从而抑制了产出下滑趋势。

从杠杆率风险来看，从第2 期生育政策调整开始，年轻（第1年龄期）居民的购房需求增加，带动房地产价格回升，导致购房和养孩成本同时上升，共同驱动居民部门负债水平回升，在产出持续下滑的背景下，居民杠杆率超越稳态值呈现上升趋势。但是，由于生育率回升有限，最初几期居民杠杆率上升幅度较小，加之企业杠杆率波动更小，总体在短期内并未造成全社会杠杆率大幅回升，带来的风险冲击不大。然而，在人口结构调整过程中，生育政策调整初期的“婴儿潮”一代逐步迈向老龄化，导致人口结构再次调整和负债水平的超调回升，从而给杠杆率造成了二次冲击，风险水平甚至超过第一次冲击。最终，随着人口结构调整完成，全社会杠杆率趋于稳定，并略高于初期稳态。

3.2.2 中等生育率的政策效应

在中等生育率情景下，生育政策作用更大，特别是在政策调整初期生育意愿的集中释放，使生育水平大幅提升，而后随着生育意愿的下降，生育率逐步回到稳态水平。在这一假定下，宏观经济变量走势如图2所示。

图2 中等生育率的经济效应

从经济增长角度来看，初期生育率下降的影响逐渐被新的生育政策抵消，从第4 期开始产出水平逐步增长，最终收敛于更高的新稳态水平。从模型的内在机理可知，生育政策调整初期，由于新出生人口处于儿童期，不仅无法提供劳动力，而且延迟了利率上升预期对储蓄的刺激作用，加之年轻居民购房和养孩支出增加，导致总储蓄水平下降。但是随着新增人口的成长带动劳动供给增加，以及利率上涨预期对储蓄刺激逐步加大，二者最终助推总产出达到新的稳态。

从杠杆率风险来看，第2 期生育政策调整幅度较大，引发房地产价格回升明显，导致年轻居民购房和养孩成本同时提升，助推负债水平连续上涨，在总产出水平下降的背景下，居民杠杆率持续提升；此外，由于企业负债下降小于产出下滑水平，导致企业杠杆率也有所增加，因而导致全社会杠杆率在最初几期波动幅度较大。最终，在经历了“婴儿潮”一代的二次冲击之后，居民和企业负债上升被更高的产出所抵消，导致全社会杠杆率略低于最初的稳态水平。

3.2.3 高生育率的政策效应

在高生育率情景下，生育政策调整的效果突出，带来人口增长更快，但受生育意愿下降影响，最终也将恢复初期稳态水平。在这一假定下，宏观经济变量走势如图3所示。

图3 高生育率的经济效应

从经济增长角度来看，初期生育率下降的影响迅速被新的生育政策抵消，从第3 期产出水平就开始回升，随着人口结构逐步调整到位，产出水平达到更高稳态值。从模型内在机理可知，在完美预期假设下，虽然生育政策调整初期增加了年轻居民的购房和养孩成本，但是对未来存款利率大幅上升的预期，刺激了其他年龄期人口的储蓄水平上升，而后者作用强于前者，导致总储蓄从初期就有所提升，并驱动资本积累水平上升；同时，随着新增劳动力的成长，共同助推产出持续增长，最终趋于更高的稳态值。

从杠杆率风险来看，从第2期开始的生育政策调整力度大，导致房地产价格大幅回升，使得年轻居民负债水平上升更为明显，再加上产出水平的小幅下滑，导致居民杠杆率波动加大；此外，储蓄的稳步回升带动企业负债增加，随着产出的回落，企业杠杆率上升也较为显著。因此，在较高生育率情景下，政策调整初期居民杠杆率与企业杠杆率的协同上升导致全社会杠杆率波动更大，风险更高。但是，随着产出水平的大幅提高，不仅削弱了“婴儿潮”一代的二次冲击，而且全社会杠杆率最终收敛于较低的稳态值。

由以上模拟结果可知，三种生育率情景下，宏观经济变量随时间变化存在一定共性，代表生育政策调整后的经济走势。从短期来看，由于政策调整初期新增人口处于儿童期，对劳动供给和储蓄的影响有限，不仅无法改变产出下滑的趋势，而且带来了年轻居民负债增加，杠杆率风险提升；从长期来看，随着新增人口逐步成长，人口结构不断优化，驱动产出水平回升，并降低了初期加杠杆的风险水平。但是，需要注意的是，生育政策调整带来的冲击更加复杂。在人口结构调整到位之前，各期波动较大，特别是生育率提高带来的“婴儿潮”。随着这期人口进入老年期，造成了产出增速下降和杠杆率提高的二次冲击，尤其对低生育率情境下的人口结构相对变化冲击更大。

此外，考虑到放开计划生育政策后，各地区生育率提高情况差别较大，正好可以对应以上三种生育率情景。因此，通过纵向对比三种情景下的模拟结果，不仅有利于识别不同生育率对全国经济增长的作用，而且有利于预测对各地区的异质性影响。对比发现，短期内，生育率水平越高，存款利率上升预期对储蓄的刺激作用越强，同时再加上人口结构调整幅度更大，共同驱动产出水平提前回升。但与此同时，在房地产需求数量和价格的共同影响下，年轻居民负债上升更快，加上更充裕的储蓄资金支撑企业负债增加，二者协同上升导致全社会杠杆率波动幅度更大，金融风险加大。长期内，生育率水平越高，经济效果越明显，不仅经济产出水平得以提高，而且进一步降低了全社会杠杆率水平。

3.3 人口流动效应的模拟分析

若将全国人口流入与流出的地区统一纳入DSGE 框架内，就需要同时考虑各地区间资本流动、贸易往来等各种关联因素，叠加生育政策调整的不同效果，将大幅增加模型的复杂程度与稳态的求解难度，且会偏离文章研究主题。基于此，该研究假定各地区为独立的经济个体，并以人口流动作为外部冲击，以更加简明的模型模拟人口生育政策调整叠加人口流动冲击对流入和流出地区的异质性影响。

3.3.1 人口流入的经济效应

根据人口流动的年龄特征，假定流动人口仅为第1年龄期的成年人口，加入人口流动的人口计算公式为：其中，imt为人口净流入变量，计算公式为：imt=itPAt-1，it为人口流动占地区总人口比例。根据2013 年以来流动人口占各省份常住人口的比例，将it设定为0.004。此外，仅设定第2 期（即2013 年）开始出现1期的人口流动冲击，同时考虑到现实中的生育政策调整并未达到高预期水平，因此叠加了中等生育率情景，从而得到图4的模拟结果。

如图4 所示，叠加人口流入冲击的模拟结果画成虚线，仅中等生育率冲击则画成实线。通过对比虚线与实线的走势可知：从经济产出角度来看，人口流入对经济增长的作用十分明显，从人口流入的当期开始，产出水平就显著高于中等生育率情景，且产出由降转升的时间提前，最终实现了产出水平的永久性增长。从模型内在机理可知，人口流入直接增加了当前劳动力水平，同时对利率上升的预期刺激了储蓄增加，驱动产出水平明显提高。从杠杆率风险角度来看，虽然流入的年轻人口增加了居民负债水平，同时储蓄增长助推企业负债上升，但更高水平的产出导致两种杠杆率变化不大，从而全社会杠杆率并未上升，其波动仅由生育政策调整所致。

图4 人口流入的经济效应

3.3.2 人口流出的经济效应

为探索人口流出的影响，假定各省稳态时经济产出相同，将it设定为-0.004，同样在叠加中期生育率情景下，得到图5的模拟结果。

由图5 所示，通过对比虚线与实线的走势可知，人口流出对经济的冲击与人口流入完全相反。简言之，劳动力人口流出直接降低了劳动供给水平，同时抑制了储蓄水平上升，导致经济产出下降；而年轻人口的减少虽然降低了居民和企业负债水平，但同时产出水平也大幅下降，导致全社会杠杆率水平变化不大。通过纵向对比人口流入和流出的模拟结果可知，吸引人口跨区域流入对经济产出的影响立竿见影，而且不会带来杠杆率风险的巨大波动，因此与生育率调整相比，既节约了等待后代成长的时间成本，又避免了杠杆率大幅上升带来的经济风险，但是对人口流出地区却造成负面影响。这一结论对各省市热衷于人才“争夺战”提供了更加直观的解释。

图5 人口流出的经济效应

4 基于经验数据的判断和预测

近年来，受计划生育政策调整与人口流动加快的影响，全国以及不同地区的宏观经济开始呈现出新的变化趋势。基于此，结合生育政策调整以来的经验数据与前文的模拟分析，初步判断生育率和人口流动情况符合的模拟情景，并预测全国和不同地区经济增长和金融风险

波动的走势。因此，从人口时空变换的角度为稳增长、防风险以及统筹区域协调发展提供决策参考。

4.1 数据说明

考虑到从2013 年底生育政策调整至今只有不到10年时间，参考数据的时间跨度为2014—2019 年。全国人口生育率数据来自世界银行与国家统计局；各地区生育率和人口流动数据来自《中国统计年鉴》《中国人口与就业统计年鉴》。此外，由于少数民族占比高的地区受生育政策调整的影响较小，因此剔除了云南、宁夏、贵州、广西、青海、新疆、西藏以及港澳台地区，选取了24个省级单位。地区人口流动则以各省人口增长与净出生人口（出生人口-死亡人口）之差占地区总人口的比重来表示。

4.2 人口因素对全国经济影响的预测

由人口出生率数据可以初步判断，自生育政策调整后，生育率开始回升，但增长幅度较小，数值更加接近中等生育率的OLG 模拟结果。结合前文中等生育率的结论可以预测，截至2021 年底生育政策调整对经济增长的刺激作用较小，且存在较长的滞后期，模型显示为20年（2期）。进一步考虑到模型设定和现实情况的差异，更长的新增人口培养周期可能会延长滞后期。此外，由生育政策调整带来的房价上涨和居民负债增加具有短期效应，由此对国内房价调控和防范高杠杆率风险带来一定挑战。

4.3 人口因素对地区经济影响的预测

由于各省人口变化同时面临生育政策调整和人口流动的影响，因此，为了区分不同地区所处的生育率和人口流动情景，以生育政策调整后各省人口出生率历年均值为横轴，以各省人口流动比率的历年均值为纵轴，分类判断并预测了人口因素对各地区经济的影响（图6）。

根据以上分类可以预测，图6 中4 个象限的地区将面临差异化的人口因素冲击。第一象限为高出生率叠加人口流入的地区，包括海南、福建、安徽、广东、浙江、重庆、四川和陕西八个省份。其中，人口流入与高出生率分别为以上地区提供了短期和长期的劳动力，共同支撑经济持续增长。但是，高出生率带来了短期杠杆率上升的风险，特别是海南和福建两个生育率更高的省份将会面临更大的冲击。

图6 人口影响因素分布图

第二象限为低出生率叠加人口流入的地区，主要包括江苏和天津两个省份。以上地区的经济增长更多依靠外来人口流入，虽然避免了生育率提高带来的风险冲击，但从长期来看，这些地区如何保持对人才的吸引力成为经济可持续增长的关键。其中，最值得关注的是天津，虽然2014—2019 年均人口流入率比较高，但2016—2019 年回落明显，人才引进力度的减弱或增加经济增长减速的风险。

第三象限为低出生率叠加人口流出的地区，包括山西、内蒙古、北京、上海、辽宁、黑龙江和吉林六个省份。以上地区的低生育率与人口流出同时存在，使得劳动力短缺问题在长短期内皆非常突出，经济增速或将持续回落。特别是东北三省生育意愿和人才吸引力的不断降低，使得经济增长下行压力不断加大。

第四象限为高出生率叠加人口流出的地区，包括山东、江西、湖南、河南、河北、湖北和甘肃七个省份。以上地区在短期内同时面临人口流出对产出的负面影响，以及高生育率带来的风险冲击。虽然高生育率提供了新的劳动供给，但如果人口流出仍然保持较高水平，将使本地培养的优质人力资源被其他地区掠夺，对经济增长的作用将明显削弱。特别是山东、江西和湖北几个人口流出严重的地区，必须更加重视本地人才的利用水平。

5 结论与政策启示

5.1 结论

为了能够准确分析人口因素对中国宏观经济的影响，在OLG 模型标准范式基础上，构建了契合国内现实的理论模型，从经济增长和杠杆率风险两个角度出发，分别模拟了生育政策调整和人口流动在长短期的异质性影响；结合研究结论和经验数据，对全国和地区经济增长和风险冲击进行了初步判断。得出如下结论：第一，从生育政策调整的时间维度看，高生育率的增长效应更加明显，但也存在一定滞后期。同时，短期内年轻居民负债水平回升明显，加之储蓄稳步增加带动企业负债上升，由此带来的杠杆率上升会造成短期风险冲击。第二，从人口流动的空间维度看，人口流动的产出效应直接且显著，而且不会带来杠杆率巨大波动的风险，因此与生育率调整相比，既节约了等待后代成长的时间成本，又避免了杠杆率大幅上升带来的金融风险，但流入和流出截然相反的作用方向或拉大地区经济差距。第三，基于全国人口增长数据可以初步判断，生育率的数值更加接近中等生育率情景，因此本次生育政策调整对全国经济增长的刺激作用较弱，且存在较长的滞后期，而短期杠杆率上升风险也需要特别关注；第四，人口时空变化将对不同地区产生显著的差异化产出效应与风险冲击。在高出生率叠加人口流入地区，短期和长期的劳动力将共同支撑经济持续增长，但高出生率带来了短期杠杆率上升的风险；在低出生率叠加人口流入的地区，经济增长主要依靠外来人口流入，同时避免了生育率提高带来的杠杆率冲击；在低出生率叠加人口流出的地区，劳动力短缺问题在长短期内皆非常突出，经济增速或将持续回落；在高出生率叠加人口流出的地区，短期内面临人口流出对产出的负面影响，以及高生育率带来的杠杆率冲击，长期内如果人口流出将明显削弱生育政策调整对经济增长的影响。

5.2 政策启示

基于以上研究结论，结合国内现实情况，该研究得出如下政策启示：第一，逐步放开计划生育政策刺激人口增长。当前，“三孩”生育政策已经全面放开，但对人口增长的刺激作用仍然较弱，要想发挥人口红利对经济增长的支撑作用，应该制定人口增长的长期发展战略，逐步全面放开计划生育政策，消除生育方面的政策限制。第二，完善生育政策的配套支持措施。生育成本过高是影响生育率回升的重要原因，因此应该进一步发挥财政补贴和税收优惠的支持作用，有针对性地推出生育补贴、教育补贴、税收减免以及购房优惠等措施，减轻家庭生育、养育、教育负担，加快释放生育潜力。第三，关注人口因素带来的杠杆率风险。生育政策调整导致杠杆率波动明显，叠加经济下行压力较大和负债水平高企的现实情况，或面临较大的风险冲击，因此应持续关注居民和企业部门杠杆率水平，强化跨周期和逆周期调节，积极防范化解人口结构调整过程中的杠杆率波动风险。第四，重视人口流动带来的区域不均衡发展。人口流动类似于零和博弈，很多落后地区成为了人口流出的重灾区，在此背景下，需要进一步加大对落后地区的支持力度，深入实施“西部大开发”“东北振兴”“中部高质量发展”等区域战略，增强地区人才流入的吸引力，促进区域协调发展。第五，积极调控人口因素带来的房价波动。房地产市场的供给不足，导致生育政策调整和人口流入都能引起房价上涨。因此，在高生育率叠加人口流入的地区，要加强房地产调控政策，促进房地产供求平衡，坚决遏制房价过快上涨，实现稳地价、稳房价、稳预期，促进房地产业良性循环和健康发展。