基于t分布变异的改进麻雀搜索算法*
2022-09-05吴超略韦文山邬贵昌
吴超略,韦文山,郭 羿,邬贵昌
(广西民族大学 电子信息学院,广西 南宁 530006)
0 引言
群智能优化算法是一种仿生算法,旨在模拟自然界中某些生物的行为或某些物理现象,因其寻优能力强、操作简单等特点,被许多科研人员研究。常见的群智能优化算法有:粒子群优化算法(Particle Swarm Optimization,PSO)[1]、萤火虫算法(Firefly Algorithm,FA)[2]、灰狼 优 化算 法 (Grey Wolf Optimizer,GWO)[3]、乌鸦搜索算法(Crow Search Algorithm,CSA)[4]和飞蛾火焰优化算法(Moth-Flame Optimization,MFO)[5]。受自然界中麻雀种群觅食行为的启发,薛建凯[6]等人于2020年提出了麻雀搜索算法(Sparrow Search Algorithm,SSA)。相比之下,该算法拥有更优的收敛率、更高的精度和易于实现等特点。但是,在算法运行的末期,SSA算法也不能避免收敛速度下降、易陷入局部最优的问题。
为了改善麻雀搜索算法跳出局部最优难的问题,加强算法运行效率,许多学者提出了有效的改进策略:吕鑫等[7]通过Tent混沌序列初始化麻雀种群,同时引入高斯变异和Tent混沌扰动对个体进行变异和扰动,使算法不易陷入局部最优点;柳长安等[8]融合反向学习策略和自适应t分布变异,引入精英粒子,扩大了算法搜索范围,增强算法后期局部搜索能力;付华等[9]在加入者位置更新时加入鸡群算法的随机跟随策略,保证多样性的同时又提高了搜索性能;Zhang等[10]利用Logistic混沌映射对种群位置进行初始化提高初始解的质量,为了加快SSA算法的收敛速度和效率,采用两个自适应参数更新发现者位置和预警麻雀数量。
以上改进措施虽然能在一定程度上提高算法跳出局部最优的能力,然而,问题仍然存在,如搜索精度不够、收敛速度不快等。基于此,本文提出一种基于t分布变异的改进麻雀搜索算法(t-SSA),该算法在加入者位置更新后,引入自适应t分布变异,对加入者位置进行扰动变异,避免陷入局部最优,提高算法的寻优精度。通过在6个基准函数上进行仿真实验,结果表明,与SSA算法相比,t-SSA算法具有更好的优化精度和更快的收敛速度。
1 麻雀搜索算法的基本原理
麻雀搜索算法(SSA)受自然界中麻雀捕食行为和反捕食行为影响,将麻雀种群抽象为三类:发现者、加入者和预警者。其中,发现者具有较高的适应度值,负责为麻雀种群寻找食物区域,并把相关区域和方向提供给加入者;为了得到更好的食物,提高自身适应度值,加入者会一直跟随具有较高适应度值的发现者,不断监视发现者进而争夺食物;当预警者发现捕食者后会立即向种群中的麻雀发出警报,此时处于种群边沿的个体会快速地朝安全区域飞去,即反捕食行为。此外,在SSA算法中,麻雀种群的发现者和加入者的身份并不是一成不变的,假如能寻觅到更优的食物区域,每只麻雀都能是发现者,不过二者在种群总数量中的比重是固定的。
在SSA算法中,麻雀种群的表示形式为:

其中,n为麻雀的数量;d为待优化变量的维度。可用下述形式来代表麻雀种群的适应度值:

其中,f(Xn)为麻雀个体的适应度值。
对于发现者,用下式表示其位置变化:

对于加入者,其位置更新公式如下:

对于预警者,数量通常占麻雀种群数量的10%~20%,且位置随机确定,其位置更新公式如下:
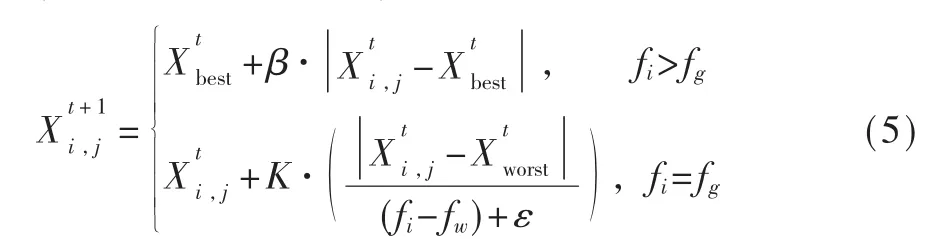
2 改进的麻雀搜索算法(t-SSA)
2.1 t分布变异
t分布又称学生t分布(Student′s t-Distribution),它的概率密度函数曲线与其自由度n有关,n的值越大,其曲线中间越高。当n=1时,有t(n=1)→C(0,1);当n=∞时,有t(n=∞)→N(0,1)。其中,C(0,1)为柯西分布,N(0,1)为高斯分布。即柯西分布和高斯分布为t分布自由度n分别为1和∞时的两个特例。t分布的函数分布如图1所示。

图1 t分布函数分布图
t分布既有柯西分布的特点,也有高斯分布的特点,本文将t分布的自由度参数用算法迭代次数代替,使t分布在算法迭代初期趋近于柯西分布,此时算法的全局寻优能力得到提升;随着迭代次数的增加,t分布又趋近于高斯分布,提高了算法的局部搜索水平,进而提高算法的寻优精度。
本文利用当前迭代次数中发现者所能搜索到的最优位置,结合t分布变异对发现者的位置进行扰动,其公式如下:

其中,Xnew表示经t分布变异扰动后的新位置;表示当前发现者所搜索到的最优位置;t(iter)表示以当前迭代次数iter为自由度的t分布;表示当前由式(4)计算得到的第i个加入者位置;fnew表示新位置的适应度值,fi表示第i个加入者的适应度值。当fnew<fi时,表示经过t分布变异扰动之后得到的新位置优于当前加入者位置,并把该位置更新给加入者。
2.2 改进的麻雀搜索算法流程
本文提出的基于t分布变异的改进麻雀搜索算法(t-SSA)步骤如下:
(1)进行初始化,并设置参数,如种群数量n、发现者数量PD、预警者数量SD、最大迭代次数itermax、安全值ST等。
(2)计算麻雀个体适应度值,记录当前全局最优值和最劣值,及其对应位置。
(3)根据设置好的发现者数量PD,挑选适应度值较好的麻雀数量当作发现者,并按照式(3)更新发现者位置。
(4)剩余的麻雀为加入者,按照式(4)更新加入者位置。
(5)应用式(6)计算出t分布变异扰动后的新位置,并按照式(7)对加入者位置进行相应的替换。
(6)根据设置好的预警者数量SD,随机选取部分麻雀作为预警者,并按照式(5)更新预警者位置。
(7)更新麻雀种群个体最优位置和全局最优位置。
(8)判断当前迭代次数是否满足算法最大迭代次数,若是,则循环结束,输出结果;否则返回步骤(2)。
3 仿真实验与结果分析
为验证本文所提出的t-SSA算法的可行性和寻优能力,本文基于Intel®CoreTMi5-7200U CPU@2.50 GHz,8 GB内存,Windows 10操作系统和仿真软件MATLAB R2019b进行仿真实验。
3.1 对比实验设计和参数设置
本文将t-SSA算法与3种基本算法:灰狼优化算法(GWO)[3]、飞蛾火焰优化算法(MFO)[5]和麻雀搜索算法(SSA)[6],分别测试6个基准函数(其中f1~f3为单峰函数,f4~f6为多峰函数),进行对比。 为确保实验的公平性,将全部算法统一设置种群数量100,迭代次数200,其余算法参数见表1。6个基准测试函数具体信息见表2。选取各算法在基准测试函数独立运行30次的结果的平均值和标准差作为实验结果,具体实验结果如表3所示,基准测试函数收敛情况如图2所示。

表1 算法参数设置

表2 基准函数信息
3.2 实验结果分析
从表3和图2能看出,在测试单峰函数f1~f3时,t-SSA算法均取得了其理论最优值,且具有更快收敛速度和更强的鲁棒性。在测试多峰函数f4~f6时,对于f4,t-SSA虽然收敛精度稍差于MFO,但与其余算法相比,其在前期的收敛速度较快;对于f5,t-SSA和SSA收敛结果相同,并且比GWO、MFO优,但从图2可以看出,t-SSA收敛速度明显更快;对于f6,t-SSA具有较好的寻优精度和较强的鲁棒性。

表3 算法优化结果对比
综合来看,本文所提出的t-SSA算法较其他算法在收敛精度、收敛速度和鲁棒性方面都有很大的提升,这表明本文所提出的改进策略是有效的,既提高了算法的寻优精度,又降低了算法陷入局部最优的概率,且拥有更好的性能。
3.3 Wilcoxon秩和检验
为进一步评估t-SSA算法的优化性能,仍需要对算法进行统计检验。因此,本文选择Wilcoxon秩和检验验证t-SSA算法每轮的优化结果是否与所对比算法存在明显区别。用P表示检验结果,当P<5%时,说明两种算法之间存在显著差异;当P>5%时,说明两种算法之间差距不明显,性能相当。在本文3.1节同样的实验条件下,t-SSA分别与GWO、MFO、SSA的详细检验结果P如表4所示,其中NaN代表两个对比算法性能接近,无法比较。
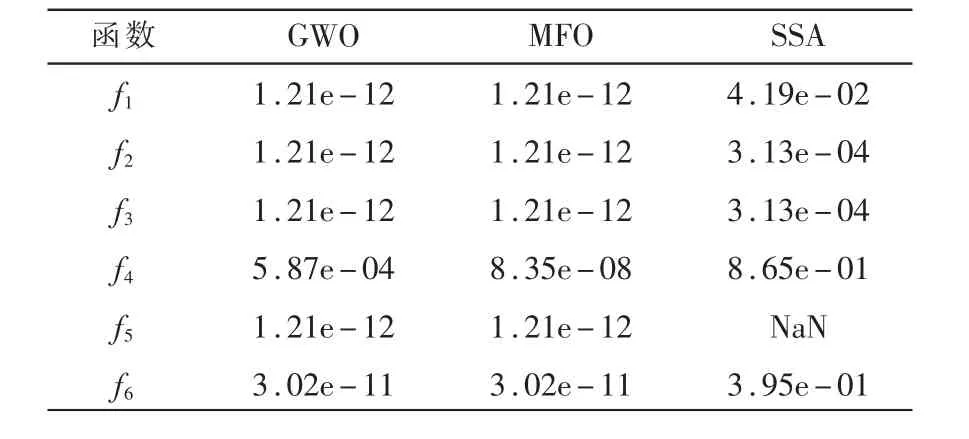
表4 Wilcoxon秩和检验结果
由表4可知,除t-SSA与SSA的f4、f6,其余大部分的P值都小于5%,这说明t-SSA算法与其他算法在统计上存在显著差异。对于f5,t-SSA与SSA差异不明显,寻优效果相当。
4 结论
为了改善麻雀搜索算法(SSA)在其运行末期出现种群多样性下降、难以跳出局部最优等问题,本文提出一种新的改进麻雀搜索算法(t-SSA)。首先,引入自适应t分布变异,对加入者位置进行扰动变异,防止跳不出局部最优点,增强算法性能。然后,通过在6个基准函数上进行仿真实验,结果证明本文提出的t-SSA的收敛精度与速度优于其他算法。综合来看,本文所提出的改进方法是有效的,能够明显提升SSA算法的寻优性能,下一步将考虑将t-SSA算法应用于实际工程问题的优化中,验证其在工程问题上的应用价值。
