基于PSO优化Bi-LSTM的交通流量预测

樊 冲

(锦州市大数据中心，辽宁 锦州 121000)

0 引言

交通运输是一个广泛的以人为本的领域，有各种各样的、具有挑战性的问题有待解决。运输系统、服务、成本、基础设施、车辆和控制系统的特征和性能通常是在定量评价其主要作用的基础上定义的。大多数交通决策都是在不精确、不确定和不完全真实的情况下做出的，有些目标和约束通常难以用清晰的值来衡量。传统的分析技术在处理变量之间的依赖关系过于复杂或定义不清的问题时被发现是无效的。此外，硬计算模型不能有效地处理交通流量的不确定性。为了解决以上问题，在过去的十年中，人们对交通和运输系统的软计算应用进行了研究，并且在此领域取得了一些重要成果[1]。

使用软计算方法建模和分析交通运输系统不仅可以处理定量或定性的问题，还可以有效地解决涉及不精确和不确定性的复杂问题。软计算可以用来弥补交通运输研究中规范决策模型和描述性决策模型之间的差距。交通问题可以分为四个主要领域：交通控制和管理、交通规划和管理、物流、交通设施的设计和建设。本课题所研究的交通流预测属于第一个研究领域。自20世纪90年代以来，软计算界一直在研究、攻克这个领域的相关问题。其中，Pamula等人[2]基于神经网络在城市交通管理系统中的应用，提出了一种基于神经网络的交通流量预测方法。Bucur等人[3]建议使用自适应模糊神经网络[4-9]进行交通预测，提出一种可以跟踪由于天气条件、季节或其他因素造成的概率分布漂移的架构。文献[10]构建了实时交通流量模型，构建模型时将自回归滑动平均模型与支持向量回归模型进行结合，克服了预测过程中的非线性问题。文献[11]为了解决模型在预测过程中会陷入局部最优问题，采用蚁群算法对基于BP神经网络的交通流量预测模型的参数进行了优化。文献[12]构建了季节性差分自回归滑动平均模型和BP的组合模型，并以实测数据对构建的交通流量预测模型进行了验证。文献[13]对城市交通流量预测时，对其进行了短时流量预测，并取得了较好的预测效果。文献[14]采用灰色极限学习机模型，实现了短时交通流量预测模型的构建，并验证了所提模型的有效性。以上研究均使用神经网络模型来进行交通流量预测，未能很好地应对交通流量强随机性对于预测结果的影响。鉴于此，本文研究了强随机性对交通流量预测结果的影响，提出了更高预测精度的城市交通流量预测模型。首先，基于双向长短时记忆(Bi-directional Long Short-Term Memory，Bi-LSTM)算法，建立了交通流量短期预测模型；其次，为了进一步提升Bi-LSTM的交通流量短期预测模型性能，采用粒子群优化算法(Particle Swarm Optimization，PSO)对Bi-LSTM模型的超参数进行寻优，确定预测模型的最优超参数组合，有效提升预测模型的泛化性，实现交通流量的精准预测。

1 基于Bi-LSTM的交通流量预测模型

因城市交通流量具有较强的波动性，选取的交通流量模型需要具有强泛化性。所以本文选择Bi-LSTM算法构建研究所需的交通流量预测模型。

循环神经网络(Recurrent Neural Network，RNN)是一种很擅长处理时间序列数据的神经网络。然而，在反向传播时，RNN不能学习到序列中早期的数据信息。由于时间序列的长度逐渐增加，神经网络会遇到梯度消失的问题。针对这一问题，长短时记忆(Long Short-Term Memory，LSTM)神经网络解决了RNN的这个局限。LSTM网络是一种特殊类型的RNN，可以学习长期依赖的信息。图1为RNN和LSTM基本结构单元。

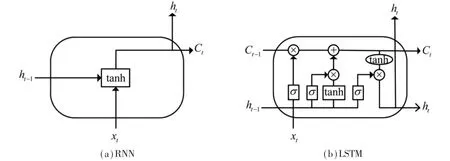
图1 RNN和LSTM基本结构单元

LSTM网络的特殊结构避免了由于复杂的重复链模块而产生的长期依赖问题。LSTM网络的关键结构是记忆单元Ct和“门”结构。LSTM网络由输入门、遗忘门和输出门组成，用于将信息更新和删除到存储单元。特别地，遗忘门可以决定过去的信息是否从一个单元状态中删除；输入门可以更新信息；输出门决定单元输出。不同门的表达式如下：

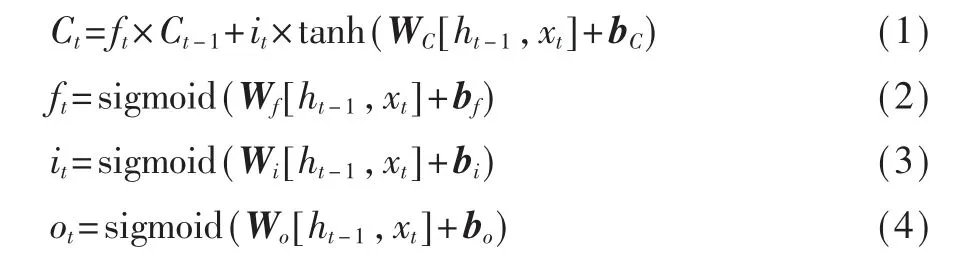
其中，xt和ht-1由隐含层的激活函数决定；Wf表示相应的权重矩阵；bf为网络偏置；ft、it分别为遗忘门、输入门的状态；sigmoid为激活函数。Ct是输入在t时刻的临时状态，tanh()是单元格的输出。ot为输出门。

在单向循环神经网络中，将学习到的前置信息用来驱动后续信息。然而，在许多情况下，预测通常需要使用整个序列的信息。双向递归神经网络结合了一个递归神经网络，预测时可实现向前和向后双向移动。LSTM网络可以将前向序列和后向序列结合起来作为递归神经网络的一种变体。在预测中，Bi-LSTM网络能够较好地考虑前后数据的内在规律。Bi-LSTM结构如图2所示。

图2 Bi-LSTM结构

对于Bi-LSTM网络，每一层的隐层状态可以表示为：

式中，LSTM()表示LSTM网络的传统运行过程；ht是隐含层前向状态；hi是隐含层后向状态；at和bt分别为隐含层前向和隐含层后向的输出权值；Ct为隐含层在t时刻的偏移优化参数；h～i为隐含层状态。

2 PSO优化的Bi-LSTM预测模型

为了进一步提升模型的性能，采用PSO算法对Bi-LSTM模型的超参数进行优化，提升交通流量预测模型的泛化性与鲁棒性，实现城市交通流量的有效预测。PSO的目的是分析群体中每个个体对环境的适应度。PSO确定该区域在环境中的最佳位置，并通过协作和信息共享向最佳位置移动。模型的性能在很大程度上取决于神经网络训练过程中模型的参数，不恰当的参数会降低模型的预测能力。神经网络参数调整的目的是获得一组能产生最佳预测性能的最优参数值。因此，采用PSO算法来识别神经网络的最优参数，在进行参数寻优时将所需参数定义为粒子群算法中的每个粒子，通过调整和迭代获得最优种群。PSO算法优化过程可以大大减少模型训练过程中的人工干预，确保最终模型具有最佳的预测效果。PSO优化Bi-LSTM模型流程如图3所示。

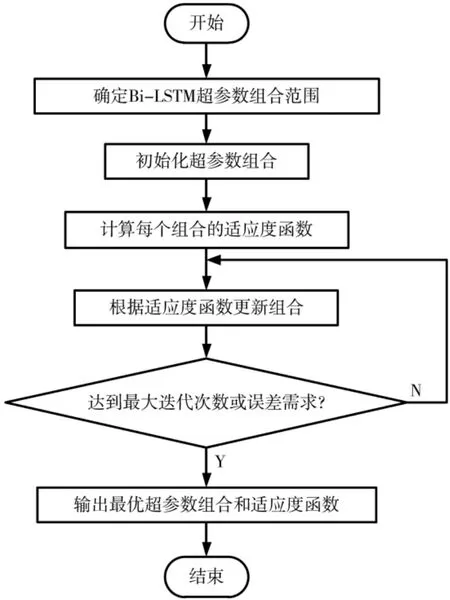
图3 PSO优化Bi-LSTM模型流程图

PSO优化Bi-LSTM模型的主要步骤如下：

(1)确定Bi-LSTM交通流量预测模型的超参数组合值范围；

(2)对Bi-LSTM交通流量预测模型的超参数组合进行初始化；

(3)计算Bi-LSTM交通流量预测模型的超参数组合的适应度函数；

(4)根据Bi-LSTM交通流量预测模型的超参数组合的适应度函数，进一步更新超参数组合，并判断是否满足误差需求，若不满足要求，继续更新超参数组合；

(5)若满足误差需求，确定最优超参数和适应度函数，由此确定本文研究所需的交通流量预测模型。

3 算例分析

为了验证本文提出的预测模型的性能优势，本研究采用绝对值平均误差(Mean Absolute Percentage Error，MAPE)、相对均方根误差(Relative Root Mean Square Error，rRMSE)、相对平均绝对误差(Relative Mean Absolute Error，rMAE)、均 方 根 误 差(Root Mean Square Error，RMSE)四个预测精度指标进行评估，各指标的计算公式如下：

为了能够有效开展交通流量预测研究，获取完备的交通流量数据集是关键环节之一。因此，在河北省唐山市某城市路段进行实测交通流量数据采集。获取的数据集包含该路段300天的交通流量数据，数据的采样间隔包括5 min、10 min和15 min 3种，每种时间间隔累积的样本数各为300个。在预测交通流量时，将获取的实测交通流量数据集中80%作为训练集，20%作为测试集。交通流量预测模型输入的特征包括待预测日前两天全部流量数据、前一天t时刻流量数据与日期类型共98维。

图4展示了5 min、10 min、15 min三个时间分辨率下的原始数据。采集到不同时间间隔下的交通流量数据样本后，可以基于不同时间分辨率的数据集开展交通流量预测。训练基于PSO-Bi-LSTM的交通流量预测模型时，采用数据集中80%的交通流量数据对模型进行训练。模型通过对历史交通流量数据的不断学习，掌握交通流量数据的变化规律，进而确定预测模型的参数。通过训练结果得出基于PSO-Bi-LSTM的流量预测模型节点个数、学习率的最优参数值分别为50和0.005 8。

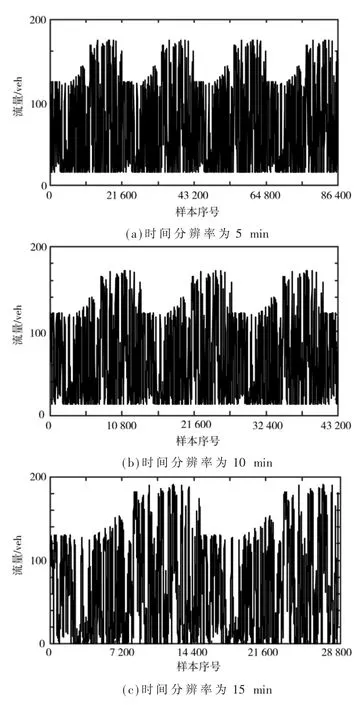
图4 不同时间分辨率下原始数据展示

在不同的时段，城市的交通流量大小变化很大。工作日，人口流动较为频繁，流量波动性会相对较强；非工作日，人口流动程度稀疏，流量波动性会相对较小。为了验证本文提出的基于PSO-Bi-LSTM的交通流量预测模型的性能优势，在测试集中选择春、夏、秋、冬四个季节的交通流量数据，同时包含了工作日和非工作日的不同日期类型，采用Bi-LSTM模型和PSO-Bi-LSTM模型分别对上述测试集的交通流量数据进行预测。开展预测时，分别采用了5 min、10 min、15 min三个分辨率下的交通流量数据。以采样间隔为15 min分辨率的数据集为例，预测分析获取的四季交通流量预测结果如图5所示。从图5可以看出，相较于Bi-LSTM模型，PSO-Bi-LSTM模型获取的交通流量预测值能够更准确地反映出交通流量的变化，并且与实际值更接近。

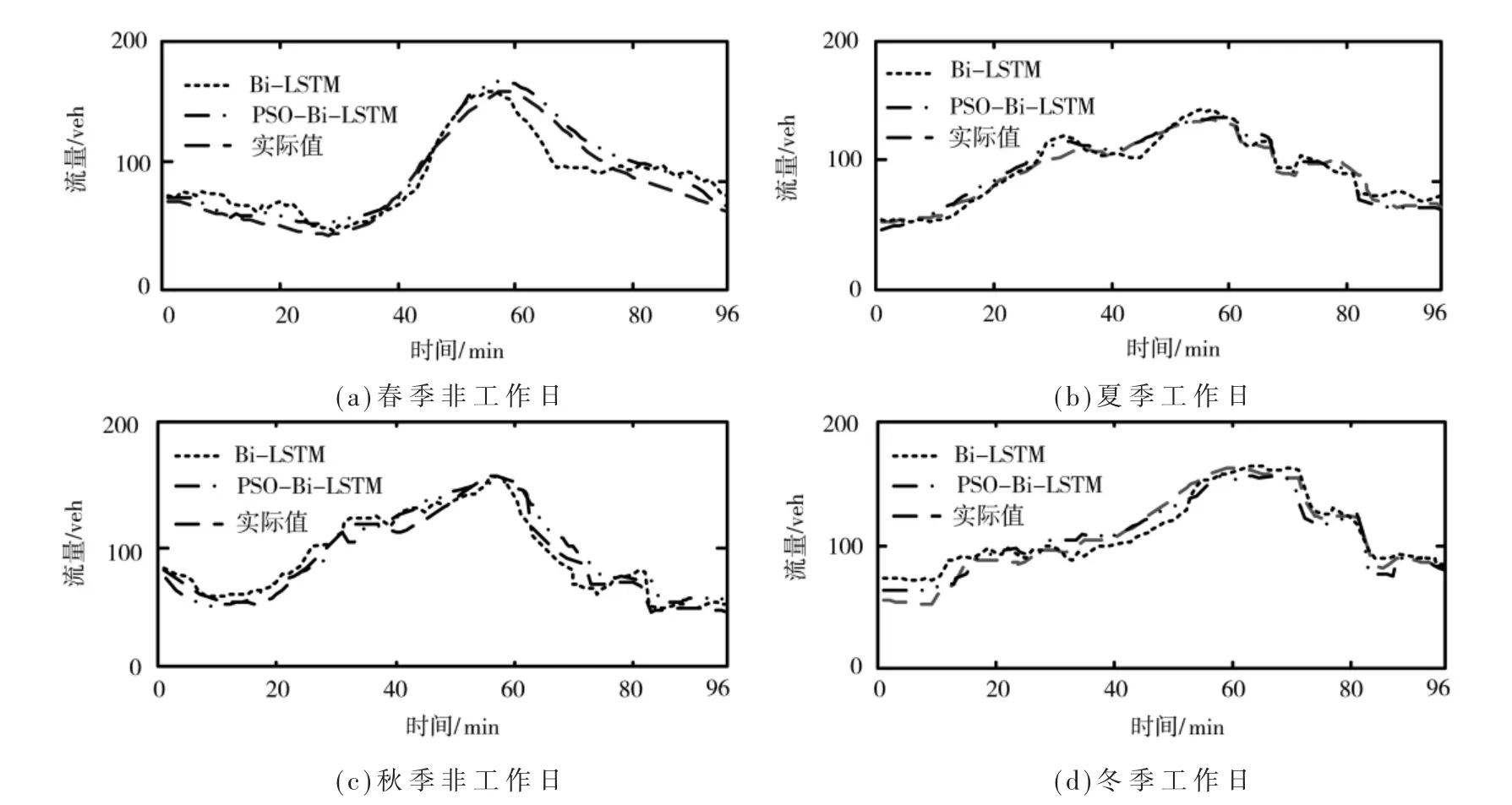
图5 两个模型不同季节的交通流量预测结果

为了进一步量化说明PSO-Bi-LSTM交通流量预测模型的优势，计算各模型预测结果的四个评价指标值，结果如表1所示。表1展示了四季典型日下，两个模型在不同采样间隔数据驱动下获取的交通流量预测结果评价指标值。通过对Bi-LSTM模型和PSO-Bi-LSTM模型预测结果评价指标的对比分析可知，PSO-Bi-LSTM模型获取的预测结果评价指标值均小于Bi-LSTM模型，效果更好。其中RMSE本身就是用来衡量观测值与真实值之间偏差的指标，其值越小，代表着与真实值之间误差越小。通过RMSE指标可以看出，本研究方法获取的预测结果与实际值更接近。由此，证明了PSO-Bi-LSTM模型对城市交通流量预测的有效性，并且此模型在不同时间采样间隔数据集下都展现出优越性能，获取了准确的交通流量预测结果。

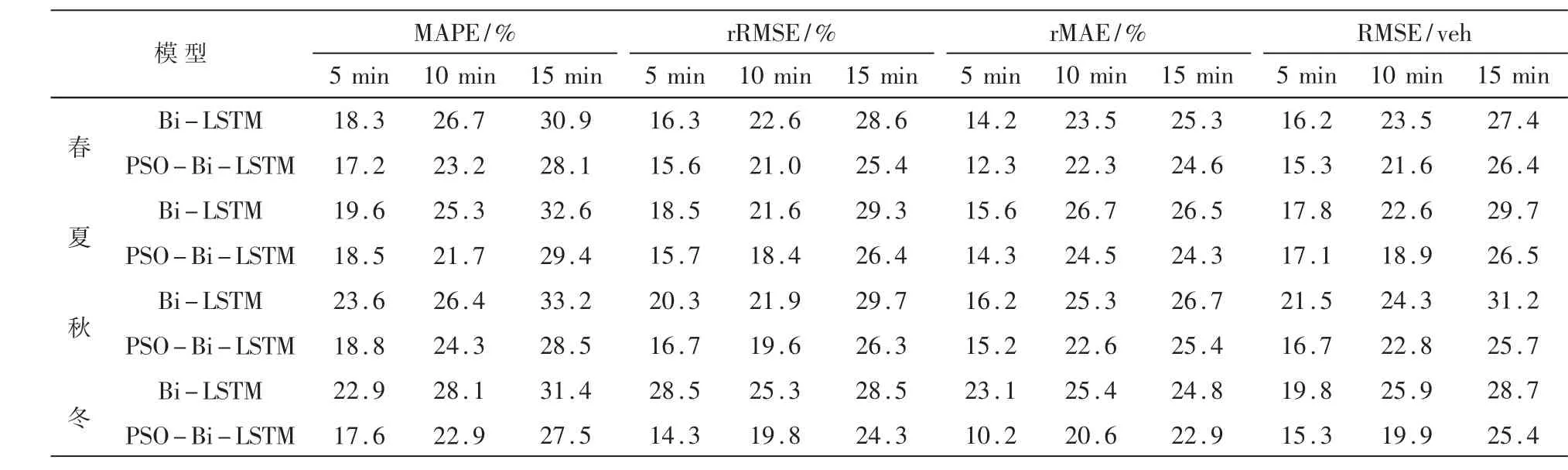
表1 两个模型不同季节交通流量预测结果的评价指标

4 结论

为有效解决交通流量具有的强随机性对预测结果的影响，本文提出了基于PSO优化双向LSTM的交通流量预测方法，实现了对城市交通流量的有效预测。取得的主要研究成果如下：

(1)为解决交通流量强波动性的影响，采用了双向LSTM模型构建交通流量预测模型；

(2)为进一步提升交通流量预测模型泛化性与鲁棒性，采用PSO算法优化双向LSTM模型的超参数，实现了对交通流量预测模型性能的进一步提升。