基于FHN神经元电路的研究性教学探索

陈 墨 武花干 徐 权

(常州大学 微电子与控制工程学院， 常州 213164)

“电子技术课程设计”是电子信息类本科专业一门重要的实践类课程。课程旨在融合“电路分析”“模拟电子技术”“数字电子技术”等多门专业课程的核心知识，提高学生应用理论知识解决实际电路问题的能力，启发学生的创新意识和创新思维[1]。国内学者已经基于虚拟仿真教学[2]、项目化教学[3]、混合式教学[4]等对该课程进行了非常有意义的探索与改革。

针对“电子技术课程设计”选题过于陈旧、缺乏创新性与时代性的问题，可引入以Fitzhugh-Nagumo(FHN)神经元电路为核心的研究性教学案例。生物神经元是神经系统处理信号的基本单元，在外界刺激的作用下可以呈现静息态、尖峰放电、簇发放电以及混沌放电等多种放电模态[5]。对生物神经元模型的复杂放电模态进行动力学分析，有助于探索生物神经网络的反应机制和工作原理。近年来，生物神经元模型的建立与应用得到了越来越多的关注，成为电子信息科学与计算神经科学领域的研究热点。在本科教学中拓展神经形态电路相关研究内容，对开拓学生的创新性思维具有重要作用，符合国家《“十四五”规划》提出的“瞄准人工智能、量子信息、基础电路、生命健康、脑科学等前沿领域，实施一批具有前瞻性、战略性的国家重大科技项目”的指导原则。

FHN神经元模型是由经典Hodgkin-Huxley模型简化得到的二维神经元模型[5]，数学模型相对简单，适合用作本科实践教学的典型案例。以FHN神经元模型中膜电位非线性关系的电路实现为切入点，设计一类改进的FHN神经元电路，并开展数学建模分析和电路仿真验证研究，内容涉及“电路分析”课程的基本元件特性和电路分析方法、“模拟电子技术”课程的运算放大器应用电路、基于Matlab的数值仿真技术，以及基于Multisim的电路仿真技术。所设计的研究性教学案例可作为“电子技术课程设计”以及电子信息类其他实践类课程的研究案例。

1 教学方案设计

(1)布置FHN神经元模型相关综述文献和研究性论文，指导学生掌握科技文献的阅读方法，了解FHN神经元模型相关研究背景和研究现状，启发学生的创新意识和创新思维[6]。

(2)以FHN神经元模型中膜电位非线性关系的电路实现为切入点，利用“模拟电子技术”中所学的半导体元器件及应用电路，对FHN神经元模型进行电路实现，得到改进的FHN神经元电路。

(3)利用“电路分析”中所学的基本元件特性和电路分析方法，推导所构建FHN神经元电路的状态方程，开展数值仿真分析。进一步的，利用Multisim电路仿真软件开展仿真验证研究。鼓励学有余力的学生，开展基于数字或模拟电路的实验测试研究。

(4)科学地分析数值仿真和电路仿真得到的数据，探寻其中存在的误差、引起误差的主要原因及其解决方案，得到一般性结论，形成逻辑严密、格式规范、语言专业的研究报告。选取优秀作品，进行研讨总结。

(5)基于研究报告、中期检查和验收汇报，从科技文献阅读能力、电路设计能力、理论分析能力、仿真软件应用和调试能力、报告撰写能力五个方面综合评定课程研究内容的完成情况。

2 FHN神经元电路实现方案

FHN神经元模型是由经典Hodgkin-Huxley模型简化得到的二维神经元模型，其数学模型为

(1)

其中含有膜电位V和恢复变量W两个状态变量，以及a、b、c、z四个系统控制参数。该模型可以模拟阳极突变激活(anode break excitation)现象和输入适应性(accommodation)，但是无法产生自发混沌或簇放电现象[5]。因此，研究者们通过施加噪声激励、引入忆阻突触等方式对经典FHN模型或电路进行改进[7]，以获得更加丰富的动力学特性。

以FHN神经元模型中膜电位非线性关系的改进和电路实现为切入点，利用反向并联二极管对的对称非线性伏安特性、运算放大器的非线性饱和特性等替换式(1)中膜电位的非线性关系，可以得到改进的FHN神经元电路。此外，亦可采用忆阻元件含有内部状态变量的特殊非线性[8]，描述FHN神经元中膜电位的非线性特性，得到更高维度、更为复杂的FHN神经元电路。基于这些特性各异的非线性元器件，可以构造出具有不同动力学特征的FHN神经元电路，为“电子技术课程设计”实践教学的开展提供丰富的研究实例，同时启发学生开展神经形态电路设计的创新思维。

3 基于分段线性电阻的FHN神经元电路

以基于运算放大器饱和特性实现的分段线性电阻为例，进行FHN神经元电路的设计，构造了一种结构简单、容易电路实现的二阶非自治FHN神经元电路，其电路结构如图1所示。为了规避交流电流源的使用，便于后续开展硬件电路测试，电路中采用交流电压源vS串联电阻R0实现非自治FHN神经元电路所需要的外加交流激励信号。

图1所示FHN神经元电路电路由电容C，电感L，线性电阻R0和R，交流电压源vS，以及非线性电阻RN构成。左侧虚线框内的非线性电阻RN利用运算放大器的饱和特性实现，当R2=R3时，其伏安关系可以描述为[9]

iN=G2vC+0.5(G1-G2)(|vC+Bp|-|vC-Bp|)

(2)

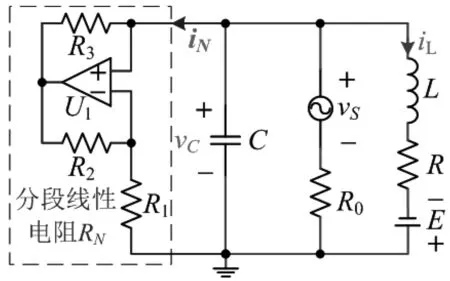
图1 基于分段线性电阻的FHN神经元电路

其中

(3)

Esat是运算放大器的饱和输出电压。当运算放大器的电源电压为15 V时，饱和输出电压Esat约为13 V。

根据基尔霍夫电压和电流定律，以及电容和电感的伏安关系，推导得到电路的状态方程为

(4)

其中，交流电压激励信号为vS=vmsin(2πft)，vm和f分别为外加激励信号的幅度和频率。

将图1的电路参数设置为vm=20 V，f=5 kHz，C=0.1 nF，E=1 V，L=10 mH，R0=20 kΩ，R=3 kΩ，R1=5 kΩ，R2=R3=10 kΩ。数值仿真时，选择电路方程的初始状态为(0 V, 0 mA)，采用Matlab仿真软件和龙格-库塔ODE23算法对电路方程(4)进行求解，进而绘制出状态变量vC或iL随外加激励幅度vm和频率f、平衡电位E等参数变化的分岔图。据此解析FHN神经元的放电模态及其随相关参数转化的情况。根据分岔图揭示的动力学演化规律，绘制出vC-iL平面的相轨图、状态变量vC的时域波形图，更为直观地观测电路的放电模态。

以平衡电位E为例。随着E的增加，FHN神经元电路由双边簇发，演化为单边簇发。而且，单边簇发的激发态持续时间随着E的增加逐渐缩短，最终演化为单周期状态。簇发放电是神经元的主要放电节律之一，其时域波形表现为静息态和激发态(即具有较大振幅的重复尖峰行为)之间的相互转迁。图2给出了E=1 V和E=0.3 V时，vC-iL平面投影的相轨图和状态变量vC的时域波形图。从图中，可以清晰地观察到神经元电路工作模态在静息态和激发态之间的转迁。而且，vC的时域波形规律地周期性重复，说明电路产生了周期簇发放电行为，而不是杂乱无章的混沌簇发放电行为。

基于Multisim电路仿真软件，搭建图3所示的电路仿真模型，对图2给出的数值仿真结果进行电路仿真验证。仿真模型中采用AD711AH运算放大器，偏置电压为± 15 V时，其饱和输出电压测量值为± 12.95 V，与数值仿真中设置的Esat基本接近。

设置仿真步长为“1e-007”，设定动态元件状态初值由任意值起振，运行仿真软件，并采用双踪示波器对电容电压vC和电感电流iL进行监测。得到的相轨图和时域波形仿真结果如图4所示。图4的电路仿真结果与图2所示的数值仿真结果，在行为特性上完全一致，但是相轨图的拓扑结构存在细微的差别。需要注意的是，当采用忆阻来构建FHN神经元电路时，可能产生依赖于动态元件状态初值的复杂放电模态[7]。对这类初值敏感的放电模态进行电路仿真时，需要为电容、电感等动态元件设定初始电压、初始电流，并将“Simulate-Interactive Simulation Setting”中的“Initial conditions”设为“User-defined”，使电路按照设定的状态初值起振，才能得到对应的放电模态。

(a) E=1 V时的周期簇发放电行为

(b) E=0.3 V时的周期簇发放电行为图2 数值仿真得到的周期簇发放电行为

结合Matlab数值仿真和Multisim电路仿真，可以对图1所示FHN神经元电路随电路参数和动态元件状态初值变化的放电行为做系统的分析。进一步地，可以利用商用元器件，制作出硬件电路开展电路测试研究。

将实验结果与数值仿真和电路仿真的结果进行对比，总结其中相吻合的特性、存在的偏差，以及引起偏差的原因及改进措施，得到一般性结论，并形成系统的研究报告。研究报告的撰写不仅要保证结果的正确性，还要注重报告格式的规范性、逻辑的严密性和语言的专业性。从细节做起，培养学生逐步养成严谨求实、认真负责、精益求精的工程素养和科学精神。

4 结语

针对“电子技术课程设计”课程选题过于陈旧、缺乏创新性与时代性的问题，提出基于FHN神经元电路的研究性教学案例，并以基于分段非线性电阻的FHN神经元电路为例，进行了数学建模、数值仿真和电路仿真研究。所设计的研究性教学案例可作为“电子技术课程设计”以及电子信息类其他实践类课程的设计内容，以有效地贯通理论课程的关键知识点，建立理论知识与实际应用之间的桥梁，也有利于启发学生的创新意识和创新思维。

图3 Multisim电路仿真模型

(a) E=1 V时的周期簇发放电行为

(b) E=0.3 V时的周期簇发放电行为图4 电路仿真得到的周期簇发放电行为