云计算环境中面向大数据的改进密度峰值聚类算法

郑冬花，叶丽珠，隋 栋，黄锦涛

(1. 广州商学院 信息技术与工程学院，广东 广州 511363，中国；2. 管理与科学大学 研究生院，雪兰莪 莎阿南 40100，马来西亚；3. 北京建筑大学 电气与信息工程学院，北京 102406，中国；4. 澳门大学 科技学院，澳门 999078，中国)

for big data samples by reasonably setting the nearest neighbor valuekofK-nearest neighbor algorithm. Compared with common clustering algorithms, this algorithm has higher clustering accuracy and efficiency, and is suitable for clustering big data samples.

Keywords: big data; cloud computing; density peaks clustering;K-nearest neighbor algorithm; decision diagram

大数据分析技术的发展给各行业生产及管理带来了新的发展机遇，通过大数据技术对企业运行过程中的各项数据进行挖掘分析，可以获得企业自身乃至整个行业的运行内在关联数据。聚类技术作为大规模数据统计分析的常用方法[1]，能够有效挖掘海量异构多维数据之间的关系，完成非标签的数据分类，为大数据各种模型分析提供数据支持。通过聚类可以将数据进行有效归类整理，提高数据的可用性[2]。在大数据聚类过程中，由于待聚类样本量较大且样本属性结构复杂，因此完成精准聚类需要较强的数据运算平台支持。云计算作为解决大规模运算问题的重要方式，可以为聚类算法的顺利实施提供平台支持。

当前，关于云计算环境的大数据聚类研究较多。孙倩等[3]将人工蜂群算法用于聚类，并通过MapReduce云平台实现并行聚类，解决了大规模数据聚类的问题。赵恩毅等[4]采用Hadoop云平台实现了大规模数据的聚类。虽然他们都充分利用了云计算环境优势，解决了聚类样本量大的问题，但是在数据聚类性能方面优势并不明显。本文中对密度峰值聚类(DPC)算法进行改进后用于数据聚类，以提高聚类适应度，采用K近邻(KNN)算法对DCP算法进行优化。根据距离矩阵计算样本点的密度值，绘制决策图并选择簇内中心点，将剩余点根据密度值分配给离中心点距离最近的类，最后将KNN-DPC算法部署至Hadoop云计算平台，用于解决大规模数据聚类的问题。

1 DPC算法

设N个样本集X被划分为m类，其数学表示为C={C1,C2, …,Cm}，C表示不同的类型，其中m≤N，且X=C1∪C2∪…∪Cm，Ci∩Cj=○/(i≠j)。

样本点xi到样本点xj的距离为rij，表达式[5]为

(1)

式中n为当前维度。

样本点xi的局部密度ρi[6-7]为

(2)

式中：rc为距离阈值；χ为密度核函数，

(3)

设核函数为高斯函数，则ρi可以表示[8]为

(4)

样本点xi所对应的最小距离δi表示为距xi最近且密度比xi大的点的距离[9]，即

(5)

根据式(4)、(5)确定点xi为簇的一个中心点。根据样本点局部密度ρi和距离δi可以生成决策图，密度值大和距离值大的被选为中心点，因此处于二维决策图右上角的点为中心点。

为了防止出现ρi和δi中一个值较大、另外一个值较小的情况，一般采用下式计算约束阈值γi[10]：

γi=ρiδi

。

(6)

然后根据ρi、δi和γi值综合选择簇中心点进行聚类。为了更加直观地表达聚类中心点的选择过程，以下采用图示方式进行说明。图1所示为样本点分布。图中的样本初始分布类别个数为3，根据各样本点的特征分布采用式(1)计算各自距离，然后根据式(4)、(5)计算样本点密度ρ和距离δ，生成的二维决策分布如图2所示。图中3个聚类中心点分别是10、12和25，选择中心点之后，按照中心点个数对所有样本点进行分类，对其余待分类的点按照样本点密度值选择离中心点距离最近的类别进行聚类。

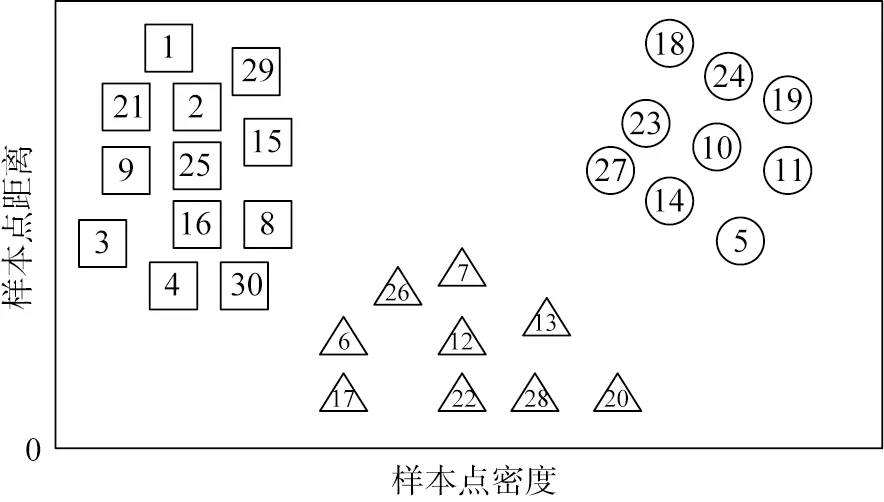
图1 密度峰值聚类算法的样本点分布

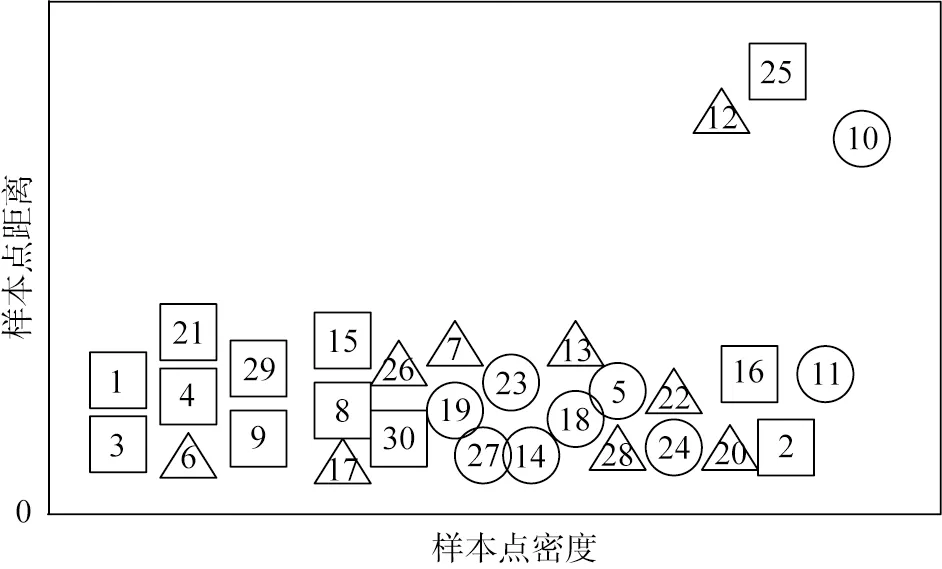
图2 基于密度峰值聚类算法生成的二维决策分布

2 DPC算法的KNN优化

在DPC算法实现过程中，rc的选择非常重要，它既决定了该算法的聚类精度，也影响着算法的执行效率。由于DPC算法受rc影响较大，对样本点分布密度不均衡的处理效果差，因此本文中采取KNN算法对DPC算法进行优化。

2.1 KNN算法

设整个待聚类的样本集为X，样本点xi∈X，dist(·)为密度距离函数，Nk(xi)表示距离xi第k近的点的集合。

xi的近邻表示[11]如下：

KNN(xi)={xj∈X|dist(xi,xj)≤dist[xi,Nk(xi)]},

(7)

K近邻的密度[12]为

(8)

(9)

采用KNN算法对DPC算法进行优化后，算法不需要再进行DPC算法的参数选择，但是需要对近邻值k进行选择[13]。

2.2 KNN-DPC算法聚类流程

在获得待聚类的样本后，计算待聚类的样本点两两之间的距离，生成距离矩阵集合，然后计算各样本点密度及距离，选择两者较大的样本点作为样本聚类的中心点，然后计算剩余样本点相对于各中心点的距离，选择较近的中心点所属类别作为各剩余样本点的类别。KNN-DPC算法聚类流程如图3所示。

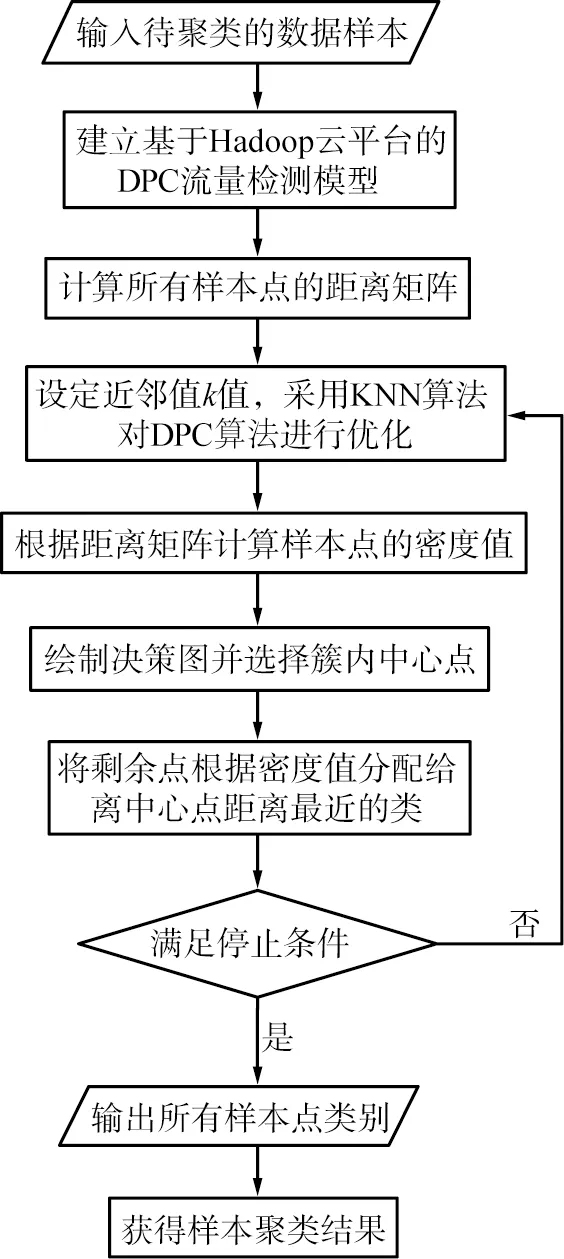
图3 K近邻(KNN)-密度峰值聚类(DPC)算法聚类流程

3 实例仿真

为了验证KNN-DPC算法在大数据聚类中的性能，进行实例仿真。云计算的Hadoop平台版本为12.1，仿真数据来源为某在线大型学习平台，样本集相关数据见表1。首先对不同样本量进行聚类仿真，生成DPC算法的决策图并分析其性能；然后分别采用DPC算法和KNN-DPC算法进行聚类操作，分析KNN算法对DPC算法的优化程度。

表1 某在线学习平台样本集

仿真的云计算环境为Apache Hadoop 2.0平台，将聚类算法打包成jar文件格式，并将数据样本和jar文件提交至Hadoop云平台。

3.1 不同样本量的决策图性能仿真

在DPC算法聚类过程中，核心内容是获得准确、有效的决策图，通过决策图选择合适的聚类类别中心点，然后根据样本点与各中心点距离获得样本类别。采用KNN-DPC算法对4个样本集求解的决策图如图4所示。

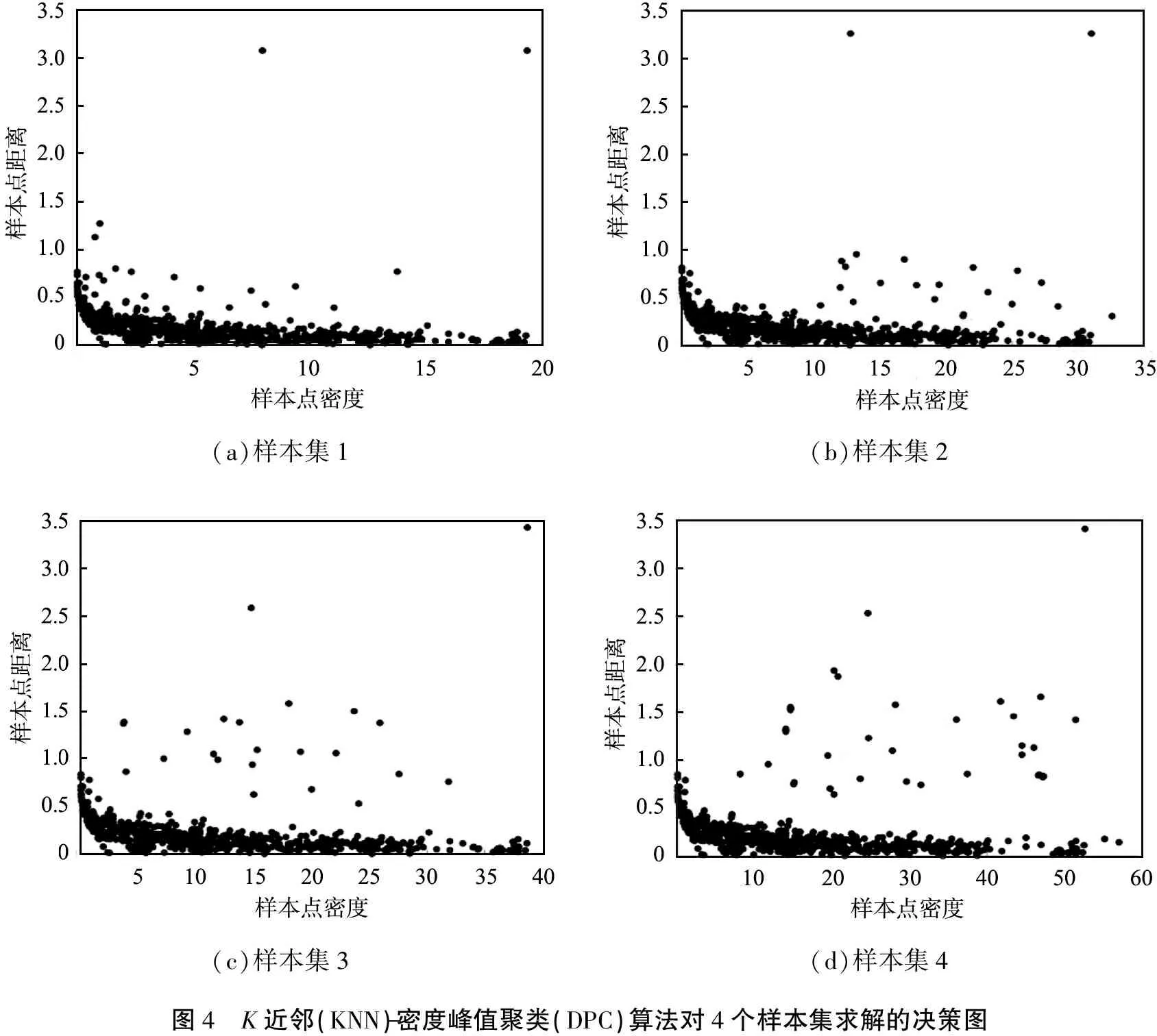
(a)样本集1(b)样本集2(c)样本集3(d)样本集4图4 K近邻(KNN)-密度峰值聚类(DPC)算法对4个样本集求解的决策图

由图可以看出： 当样本个数为1 000时，大部分样本点分布在δ<1的范围内，样本点的ρ分布范围较广；当样本个数为2 000时，大部分样本点仍分布在δ<1的范围内，但相比于样本个数为1 000时，ρ较大的样本点增多；当样本个数为3 000时，δ>1的样本点逐渐增多，ρ较大的样本点也在增加；当样本个数为4 000时，相比于前3种样本量，处于δ>1且ρ>30的样本点数显著增加。图中位于坐标轴右上角的样本点δ变化较小，但ρ明显增大。总之，随着样本数量增加，样本点局部密度ρ最大值增大，但δ变化较小，原因是在聚类中心数不变的情况下，样本数量增加使得聚类中心阈值范围内的样本点数增多，从而样本点局部密度值增大。因为聚类中心点个数没有发生变化，所以样本数量增加对影响较小。

采用KNN-DPC算法对4个样本集进行聚类准确率仿真，结果如表2所示。从表中可以看出，当样本个数从1 000增至4 000时，平均聚类准确率提升了1.84%。随着样本数量增加，在进行KNN算法的近邻密度求解时能够更全面地获取样本点的密度，促使DPC算法获得更优的聚类效果，从而提升了聚类的准确率，表明KNN-DPC算法特别适用于大数据聚类。

表2 K近邻-密度峰值聚类算法的

3.2 KNN算法的优化性能

为了验证KNN算法对DPC算法的优化性能，分别采用DPC算法和KNN-DPC算法对样本集4进行聚类仿真，并求解2种算法的聚类准确率及标准差，结果见图5。

(a)聚类准确率

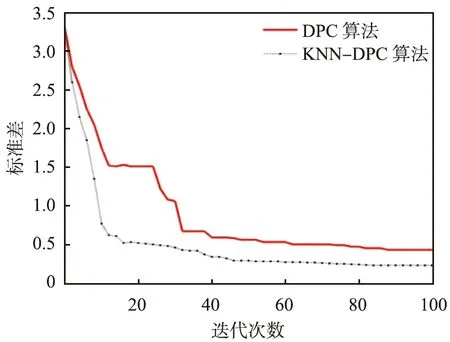
(b)标准差KNN—K近邻算法；DPC算法—密度峰值聚类算法。图5 不同算法的聚类准确率及标准差

从图5(a)中可以看出，KNN-DPC算法的聚类准确率明显高于DPC算法的，KNN-DPC算法收敛时准确率约为0.95，而DPC算法的仅为0.83。从聚类时间来看，稳定时DPC算法的聚类时间约为24 s，而KNN-DPC算法的聚类时间约为27 s，原因是引入KNN优化后，聚类需要消耗更多的时间，但两者差距并不大。从图5(b)中可以看出，DPC算法和KNN-DPC算法的聚类准确率标准差快速减小直至稳定，在迭代82次后，KNN-DPC算法达到稳定，标准差收敛于0.23左右，而DPC算法迭代90次后标准差才收敛于0.43，因此从聚类稳定性来看，KNN-DPC算法优于DPC算法。

通过对比可以看出，KNN-DPC算法比DPC算法需要较长的聚类时间，但是前者迭代次数更少，原因是引入KNN算法优化后，DPC算法能够获得更优的距离阈值，在相同聚类准确率阈值条件下，虽然KNN算法优化需要消耗时间，但算法达到收敛时的迭代次数更少，降低了聚类模型复杂度。

3.3 不同算法的聚类性能

为了验证不同算法的大数据聚类性能，分别采用常用的模糊聚类算法[14]、K均值聚类算法[15]、卷积神经网络(CNN)算法[16]和KNN-DPC算法对样本进行仿真，仿真样本来自公开的UCI机器学习数据库，如表3所示，不同算法的聚类准确率和标准差结果如表4、5所示。

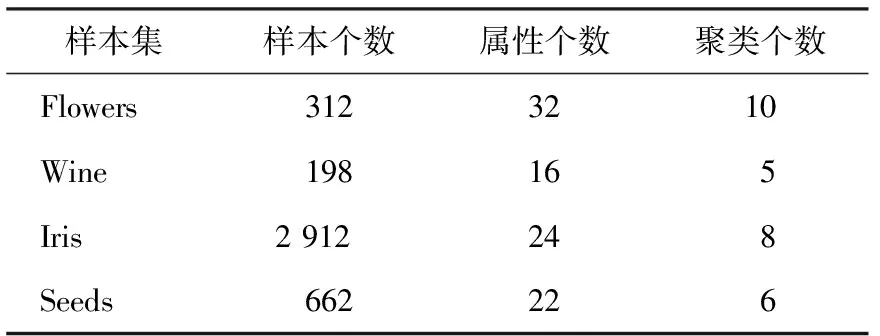
表3 聚类算法仿真数据集

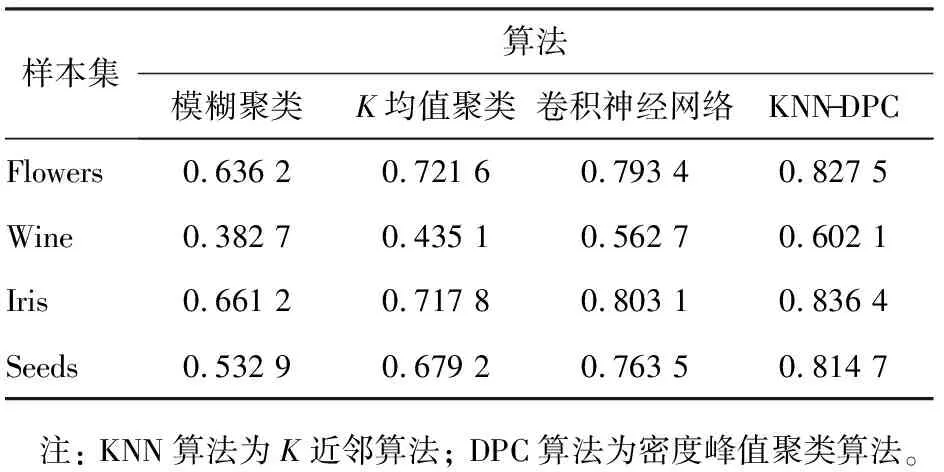
表4 不同算法的聚类准确率

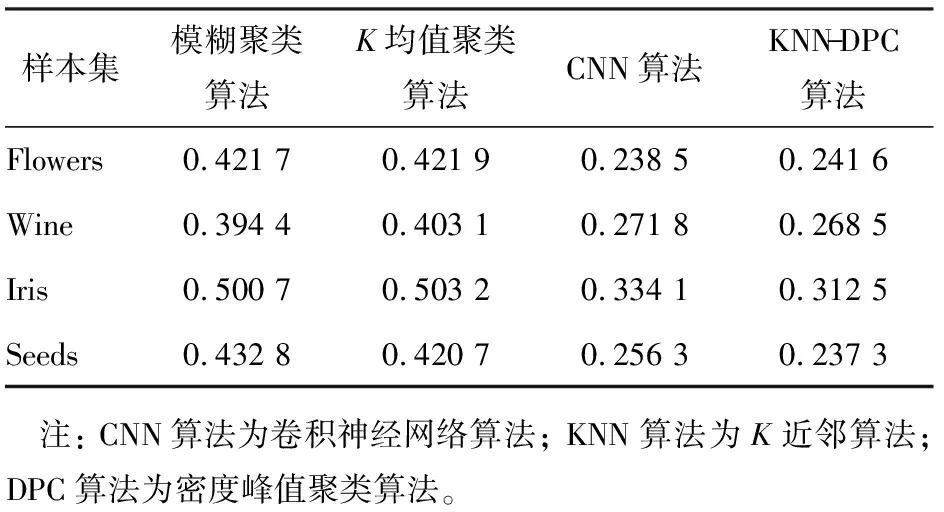
表5 不同算法的聚类准确率标准差

从表4中可以看出，4种算法对4个不同类别样本集的聚类性能差异明显，KNN-DPC算法在4个样本集中的聚类准确率均最高，CNN算法的次之，模糊聚类算法的最低。4种算法在Iris样本集中的聚类准确率最高，在Wine样本集中的聚类准确率最低，其中KNN-DPC算法在Iris样本集中的聚类准确率达到0.836 4。从表5可以看出，KNN-DPC算法和CNN算法收敛时的聚类准确率标准差明显小于模糊聚类算法和K均值算法的，其中KNN-DPC算法在Seeds样本集中的聚类准确率标准差最小，仅为0.237 3。

4 结语

本文中将KNN算法优化的DPC算法应用于大数据聚类，能够获得较高的聚类准确率，通过合理设置KNN算法中参与局部密度计算的近邻值k，求解DPC算法的核心参数样本局部密度和距离，选择两者中数值较大的点作为聚类中心点进行聚类，与常用聚类算法对比，KNN-DPC算法具有更高的聚类准确率且聚类效率高，适用于大数据聚类。