HSM标准模型的风噪声源及其特性分析*
2022-09-05胡兴军毛靖铭张扬辉刘一尘马家义乔俊贤余天明
胡兴军,毛靖铭,张扬辉,刘一尘,马家义,乔俊贤,余天明
(1. 吉林大学,汽车仿真与控制国家重点实验室,长春 130022;2. 一汽奔腾轿车有限公司,长春 130022)
前言
随着我国汽车技术的发展,消费者对汽车品质的追求日益增加。噪声是客户对汽车品质最直观的感受。高速行驶时,气动噪声对驾乘舒适性的影响越来越重要。随着电动汽车的兴起,由风噪引起的内部噪声受到越来越多的关注。如何对内部噪声进行有效仿真以探究内部噪声特性也一直是研究热点。
仿真计算是研究汽车风噪的重要手段,但是以往多数仿真计算只针对外部噪声,评价指标为外部监测点,对内部噪声特性研究较少。近年来,不少国内外学者开始研究内部噪声计算。2017 年,Schell等提出了有限元、边界元和SEA 的广义边界方法相结合的方法,可用于计算宽频的车内噪声。2020年,Hu 等采用不可压缩CFD 求解器和振动声学模型计算商用车外流场特性和内部声场响应。2021年,Wang 等用不可压缩的LES 与有限元法结合计算乘用车的内部噪声,研究了车底流动噪声对车内噪声的贡献。计算车内噪声时,声源来源越广,计算资源和时长要求越高,由于外部声源构成复杂,声源选取困难,因此研究车内噪声时,如何合理有效地选择仿真声源十分重要。
本文中以HSM(Hyundai simple model)标准模型为研究对象,通过实验与仿真研究以驾驶员耳侧噪声水平为目标时,合理声源的选择及声源成分与其对内部噪声的贡献。分为实验、流场和声场仿真3个部分。在实验部分中对HSM 标准模型的实验数据进行分析,研究不同噪声源对内部噪声的贡献及其受风速影响的变化规律;在流场和声场仿真部分中基于实验结果分别验证流场和声场仿真结果,并对流场结构和噪声源成分及其贡献度进行分析,由隔声理论对成分差异的机理做出阐释。由此获得通用性结论,为实际车型风噪控制提供仿真策略和指导。
1 实验部分
1.1 HSM标准模型
HSM 标准模型是一种可用于车内噪声实验和数值研究的模型。本次实验所用HSM标准模型构成及连接方式如图1 所示,其外廓尺寸长为2 m,宽和高各1 m(××= 2 m × 1 m × 1 m),模型除车窗外,其余部件均为铝结构,车窗玻璃统一为4 mm 普通钢化玻璃。模型整体使用密封胶进行密封,防止泄露噪声的出现。
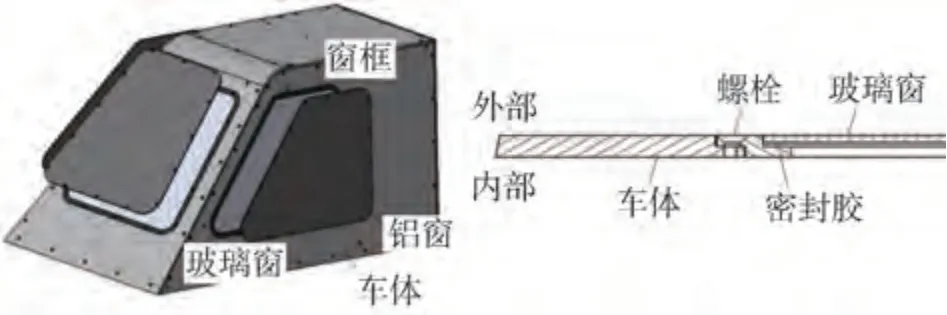
图1 HSM标准模型
为保证车窗是内部噪声的唯一声源,对模型内部进行噪声控制处理(NCT)。针对铝表面的传声区域,在模型内部进行如图2 所示的噪声处理,记为NCT_1,而玻璃表面的传声区域,内部不做任何处理,记为NCT_2。
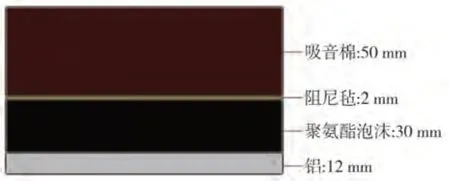
图2 HSM标准模型内部声学处理布置图
1.2 实验设置
本次噪声实验在吉林大学汽车风洞实验室进行,混响实验在一汽轿车半消声室进行。
1.2.1 表面压力测量实验
考虑到HSM 标准模型本身的对称性,仅在模型左侧窗进行表面压力测量。实验风速为120 km/h,测量点在侧窗横纵方向上均匀布置,实验测点及装置布置如图3所示。

图3 表面压力测点及装置布置图
1.2.2 内部噪声测量实验
内部噪声实验的测点参照文献[6]中布置在驾驶员左耳侧,实验共设置5 种测量工况,分别为全铝窗、全玻璃窗、单左侧玻璃窗、单右侧玻璃窗和单前玻璃窗,如图4 所示。其中单侧玻璃窗工况表示实验布置时仅有该侧为玻璃窗,其余车窗为经如图2所示的噪声控制处理的铝窗。测量各工况在不同风速下内部测点的噪声水平。

图4 内部噪声测量布置图
1.2.3 混响时间测量实验
为提供后续声场仿真所需对腔内材料吸收与反射作用的模拟参数,进行混响时间测量实验。本实验一共设计3 个方案,各方案下体积声源分别置于HSM 标准模型地板的前中后3 个位置进行发声,对于每种声源位置,均采用模型前后的两个传声器进行测量,不同方案中传声器位置保持不变,每种方案下重复测量3次,实验布置如图5所示。

图5 混响时间测量布置图
1.3 实验数据分析
1.3.1 表面压力测量实验分析
图6为表面压力测量结果。由图可知,侧窗表面压力波动呈现明显的规律性。纵向上表面压力数值呈先减小后增大的趋势,存在明显拐点。由此可见,侧窗上存在一条压力分界线。
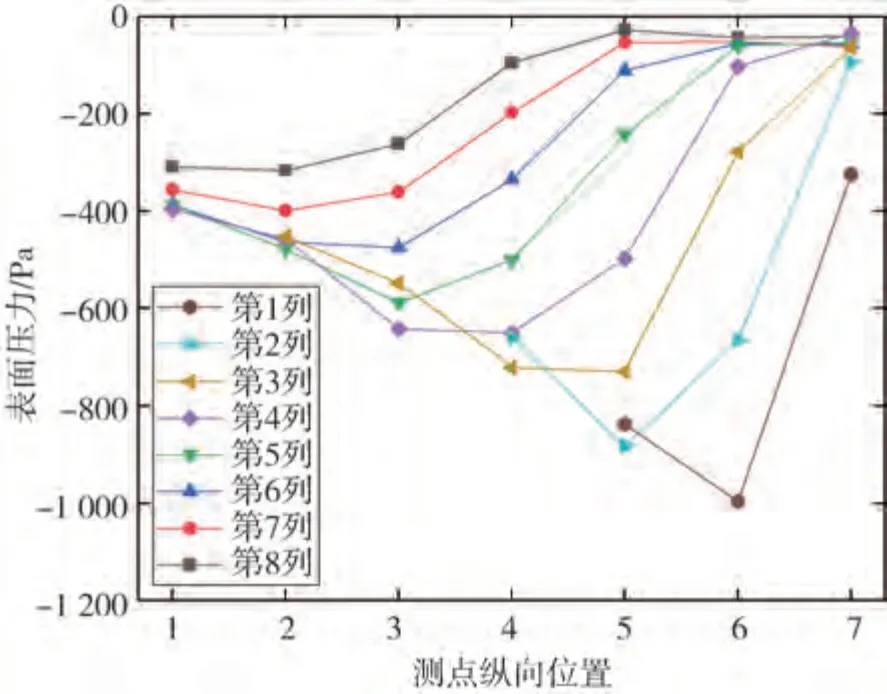
图6 左侧窗表面压力曲线
结合各拐点位置,拟合得到如图7 所示的压力分界线。侧窗压力分界线与水平方向的夹角约呈30°,由此推测实际侧窗压力分界线与水平方向约成29°~30°的夹角。
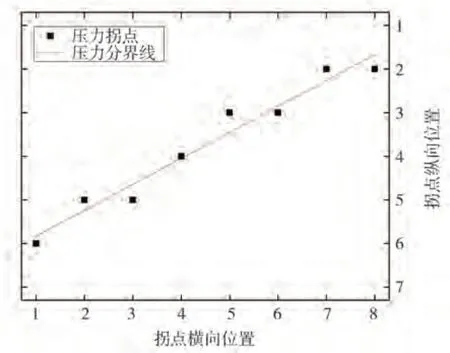
图7 侧窗压力分界线
1.3.2 内部噪声测量实验分析
(1)风速对内部噪声的影响
图8为不同工况下不同风速测点噪声的频谱图。由图可知,随风速增加,各工况的频谱曲线变化规律随风速变化基本保持不变,而车内声压级随之增加,但不同工况下声压级受风速影响而变化的频段不同。对全铝窗、前玻璃窗和右侧玻璃窗而言,风速增加对其声压级的影响集中在1 200 Hz 以下;1 200~4 000 Hz 之间,声压级波动很小。对全玻璃窗和左侧玻璃窗来说,声压级在全频段上均随风速增加而增长,但增长幅度随频率增大而减小,在1 200 Hz 附近,全玻璃窗受前玻璃窗和右侧玻璃窗突变的影响,其随风速变化的趋势有明显波动。

图8 不同工况下测点噪声频谱图
(2)各窗对内部噪声的贡献度分析
120 km/h 风速下,各玻璃车窗工况的频谱图如图9 所示。由图可知,右侧与前玻璃窗的频谱曲线基本一致,仅在100~800 Hz 频段内右侧玻璃窗的声压级略高于前玻璃窗;左侧玻璃窗的频谱曲线在全频段内均与全玻璃窗相似,仅在1 000~2 500 Hz 之间存在差异,但对总声压级影响有限,两者总声压级相差0.89 dB,仍十分接近;全频段内,左侧玻璃窗频谱曲线高于前玻璃窗和右侧玻璃窗,在1 000~2 500 Hz以内,尤为明显。由此可知,针对测点噪声声压级,各窗的贡献度依次为:左侧窗>右侧窗>前风窗。

图9 各玻璃车窗工况的频谱图
(3)传声效率差异分析
全铝窗与左侧玻璃窗的频谱图如图10 所示。由图可知,除400~800 Hz 频段外,其余频段上左玻璃窗的声压级均高于全铝窗,在1 000 Hz 以上的中高频段内,这一现象尤其明显。由此说明,在全频段内(除400~800 Hz 外),NCT_1 对车内测点的传声效率低于NCT_2。
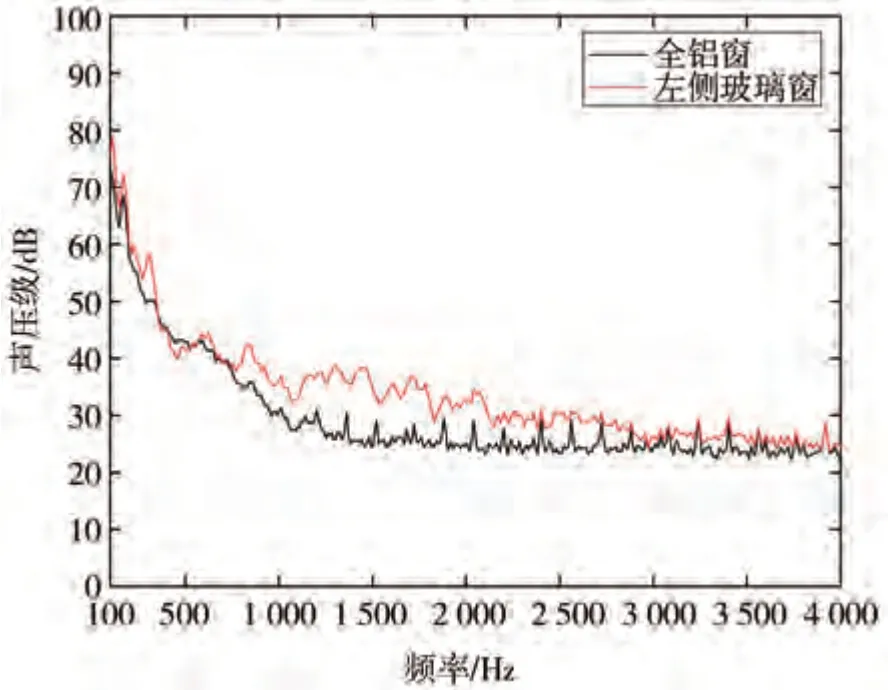
图10 NCT的传声效率对比
结合文献研究可知,驾驶室内部噪声主要来源于汽车侧窗区域。基于实验分析可得:在左侧玻璃窗工况下,车体和其他车窗对测点噪声的贡献可以忽略,且左侧窗下的内部噪声情况与全部声源存在下的内部噪声较为接近。因此研究驾驶员左耳位置处的噪声水平时,只以左侧玻璃窗作为声源合理可行。而针对400~800 Hz 之间可能带来的误差,由于其声压级较低,对总声压级影响较小,因此误差应在可接受范围内。
1.3.3 混响时间测量数据处理
根据文献[7]处理混响实验数据,得到HSM 标准模型的混响时间。由计算流体等效阻尼系数,将其作为声速的虚部,为声学仿真提供声学计算参数,声速设置如表1所示。
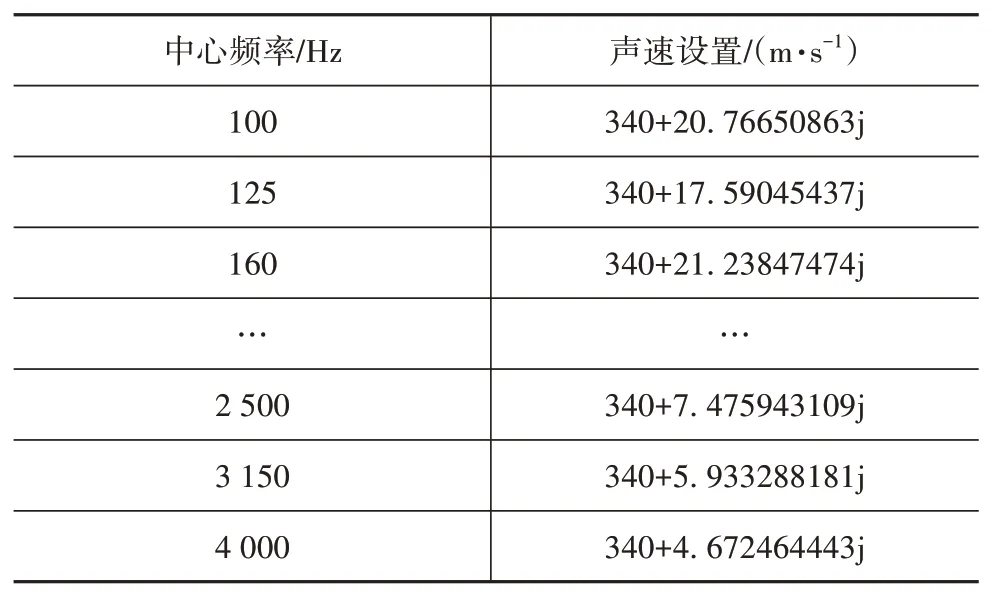
表1 声腔内部流体声速设置
2 流场仿真
采用计算气动声学方法进行流场仿真求解,研究内部噪声的成因,并与实验对比验证流场仿真准确性。
2.1 流场仿真模型与计算设置
由于计算资源和时长的限制,同时考虑到HSM标准模型本身具有对称性,故流场仿真中仅使用HSM 标准模型的左半侧作为仿真模型。流场仿真模型及监测点如图11所示。

图11 流场仿真模型及监测点布置示意图
流场仿真计算域及加密区设置如图12 所示。计算域的阻塞比为3.3%,满足仿真要求。采用切割体网格和棱柱层网格划分计算域,加密区尺寸依次为2、4、8、16和32 mm。
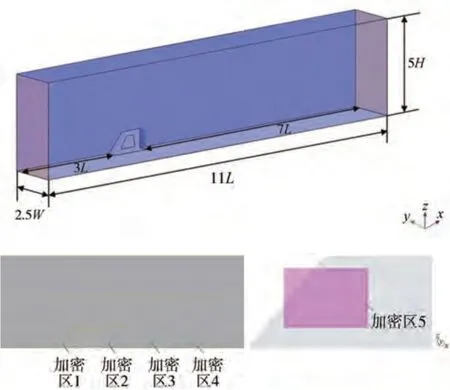
图12 流场仿真计算域及加密区
流场仿真时首先通过稳态计算以初始化流场,为后续计算提供初始值,然后进行瞬态计算,采用直接计算气动噪声法求解,同时计算流场压力和声场压力。时间步长Δ为1.25 × 10s,计算时间为0.2 s,0.1 s后开始采样。本文边界条件与求解设置如表2~表4所示。

表2 边界条件设置
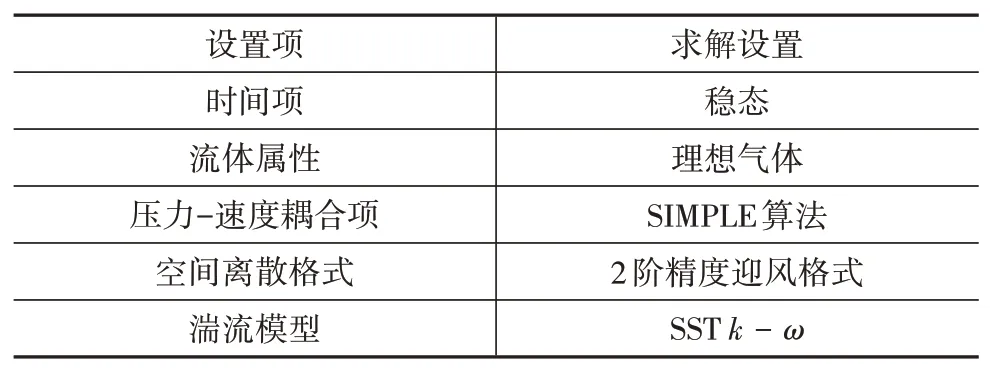
表3 稳态求解设置

表4 瞬态求解设置
2.2 流场仿真分析
2.2.1 流场结构分析
方法为第二代涡识别方法,可识别流场涡结构。基于Cauchy-Stokes分解,表达式为

式中、分别为速度梯度张量的对称与反对称部分。
图13为等值面图(=800000.0 s)。由图可看出涡的分布与结构。来流受到HSM 标准模型前缘的阻碍而分离,产生分离涡,该涡随气流向后发展一段距离后,重新附着在模型表面。分离涡的存在区域随向升高,逐渐朝向扩展,其再附着位置也随着向升高朝向延伸,形成一条倾斜的再附着线。仿真得到再附着线与水平方向约呈30°,如图13 所示。与实验结果吻合度较高。由此说明仿真所获得的流场结构准确性较高。
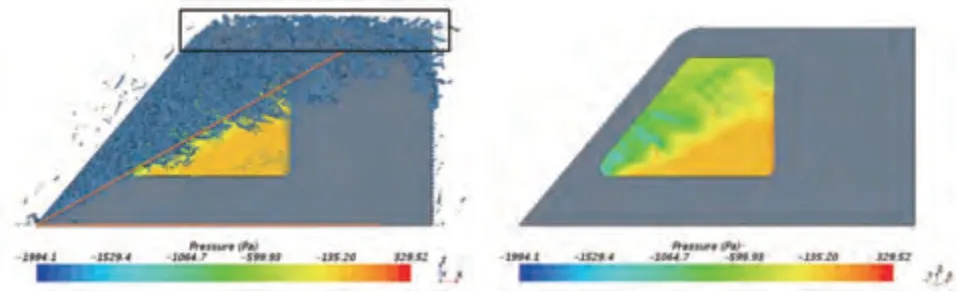
图13 Q等值面图及侧窗压力云图
由图13 可知,模型前缘分离现象随向升高逐渐减弱,当气流遇到弧形过渡时,这部分气流并不在过渡位置发生明显分离,而是继续向后发展与顶部侧边作用产生向侧面发展的涡结构,如图13 黑色区域所示。从图中可明显看出,黑色区域的涡结构在强度上不如前端产生的分离涡,且作用区域基本没有进入侧窗,而分离涡的范围则占据了侧窗的左上部分。从压力云图可以看出,侧窗表面左上部分和右下部分之间存在较大的压力梯度,侧窗表面压力脉动剧烈,中间的压力分界线与分离涡再附着线基本一致,这说明侧窗表面剧烈的压力脉动是由模型前缘的分离涡引起。综上可知,通过侧窗向内传递的噪声主要由分离涡引起。
2.2.2 流场声源分析
对于汽车气动噪声,偶极子和四极子声源为主要噪声源,因此基于宽带噪声源模型对声源进行分析。
(1)偶极子声源分析
在假定各向同性的湍流场内,Curle 模型可以计算偶极子声源产生的声音,如图14 所示。由图可知,在HSM 标准模型侧面靠近前缘的位置,存在一倾斜向上的强声源分布,声功率强度在100 dB 左右,且越靠近模型底部,强度越高,为主要偶极子声源。该声源的位置与上述分离涡再附着位置基本一致。由此可知,该处声源是由分离涡再附着引起模型表面剧烈压力脉动而产生的。
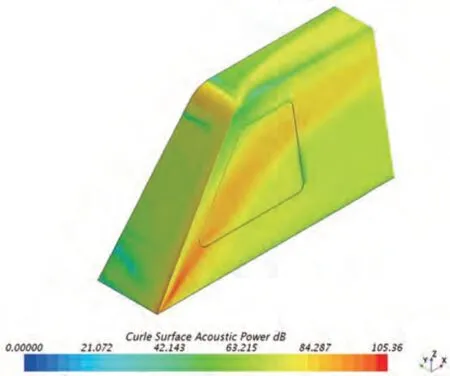
图14 HSM标准模型表面Curle声功率分布云图
(2)四极子声源分析
在假定各向同性的湍流场内,Proudman 模型可以评估流场中湍流产生的四极子声源造成的局部影响。图15 为湍流结构在HSM 标准模型的不同向位置的流场内产生的四极子声源。由图可知,在同一水平面上,四极子声源朝和向扩散,且以向为主要传播方向,随向的增大,四极子声源作用范围在和向上扩展,但仍以向为主,且声源强度的核心区也随向增加逐渐朝向移动,但声源强度随向增加而减小。根据四极子声源作用范围终止点的迁移可以看出,四极子声源在模型侧面产生了倾斜向上的作用区,随向升高,作用范围增大,作用强度减弱,这一现象与模型前缘分离涡的效果一致。由此可知,四极子声源是由分离涡引起模型侧面前端附近的涡流运动剧烈而产生的。

图15 HSM标准模型表面Proudman声功率分布云图
综上所述,模型前缘产生的分离涡及其再附着现象是车内噪声的主要成因。
2.3 流场仿真结果验证
通过仿真计算得到表面压力监测点的瞬态结果,将其平均后与各测点的表面压力实验数据进行对比,结果如图16 所示。由图可以明显看出,仿真结果与实验数据具有一致性。
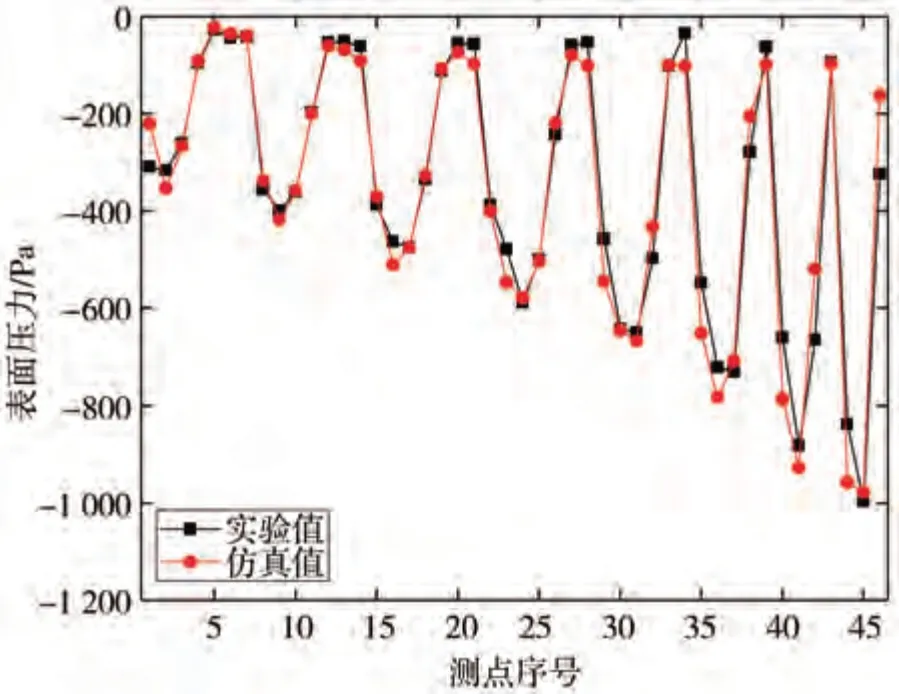
图16 表面压力实验与仿真对比图
将仿真计算得到表面声压级监测点的瞬态结果,经傅里叶变换得到1/3倍频程曲线。鉴于本次实验条件的限制,未能对侧窗外表面的声源信息进行测量,因此选择HSM 标准模型实验的文献[10]进行表面声压级的验证。实验与仿真的对比结果如图17 所示。从图可以看出,仿真结果与参考实验数据具有良好的一致性,各中心频率下的差异在10%以内。
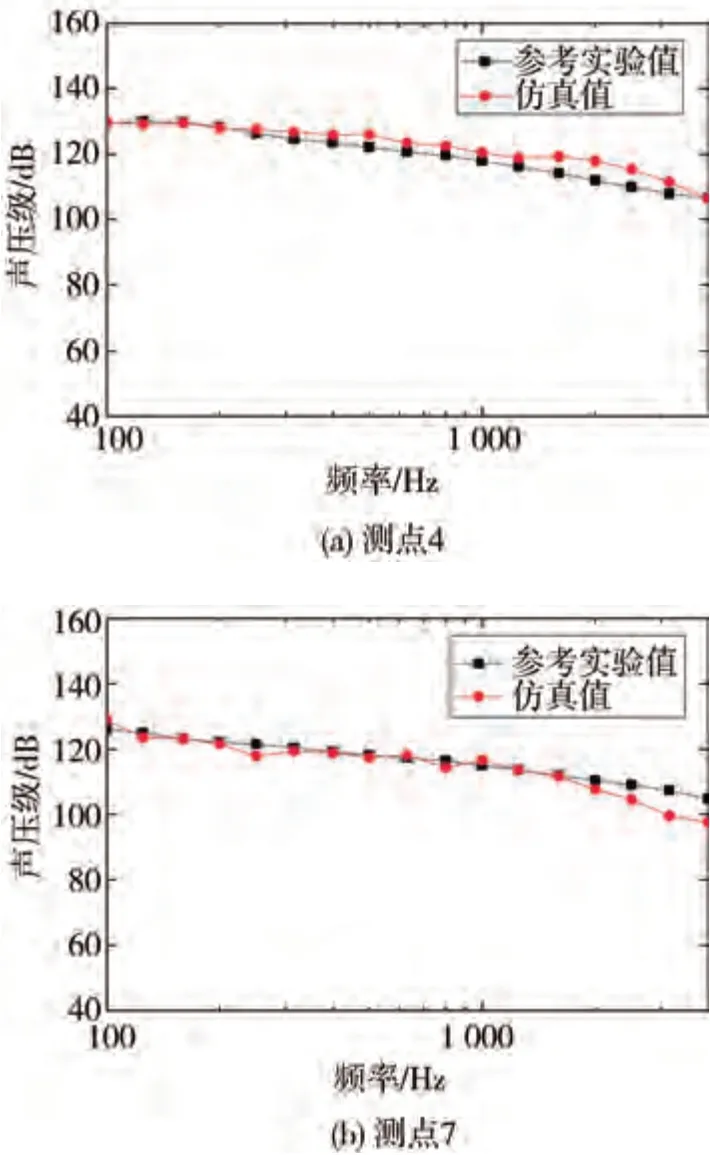
图17 表面声压级实验与仿真对比图
由以上对比结果可以说明,本文中采用的流场计算方案具有较高准确性。
3 声场仿真
采用ACTRAN 声学求解器对HSM 标准模型进行内部声传播计算,并与实验对比验证声场仿真准确性。
3.1 声场仿真模型与计算设置
根据实验模型的内部声腔建立声场仿真所用的声腔模型,内部监测点与实验测点保持一致,声场仿真模型及监测点的布置如图18所示。

图18 声场仿真模型及监测点
声场计算时,为保证声传播的计算精度,声腔模型的体网格尺寸与求解频率应满足:

上式表示目标求解频率所对应的一个声波波长应包含6~8 个网格,其中为声速,Δ表示声腔模型的最小网格尺寸。
本文目标求解频率为4 000 Hz,综合求解精度和计算时长考虑,声场仿真模型上声源加载区网格尺寸为2 mm,网格节点与流场仿真模型一一对应。声场仿真的计算设置如表5所示。

表5 声场仿真计算设置
3.2 声场仿真分析
3.2.1 声源激励成分分析
定义5[1,7] 设μ:X∪Y→X∪Y上的映射,若N>M≥2,对任意的Xi∈X,Yj∈Y,满足:μ(Xi)∈Y,μ(Yj)∈X∪{Yj}和μ(Xi)=Yj,μ(Yj)=Xi,则Xi和Yj在μ中匹配,称(Xi,Yj)为双边匹配对。若(Xi,Yj)是μ中任意的双边匹配对,且μ(Xi)≠Yj′,Yj′∈Y,Yj′≠Yj,μ(Yj)≠Xi′,Xi′∈X,Xi′≠Xi,则称μ是一对一双边匹配,μ(Yj)=Yj表示Yj在μ中未匹配。
流场计算得到的声源激励由两种成分组成:一是流场中涡结构本身作为声源,向周围辐射声波,这种声源激励被称为声学压力脉动(acoustic wall pressure fluctuation,AWPF);另一种是流场中流体与结构直接作用,引起结构边界发生振动而形成的声源,被称为湍流压力脉动(turbulent wall pressure fluctuation,TWPF)。
表面压力激励由PMD 分解得到图19。由图可知,湍流压力脉动与侧窗表面压力脉动基本重合,随着频率的升高,差异逐渐显现,但差距始终较小,而声学压力脉动在全频段上,数值远小于湍流压力脉动,两者之间的差距随频率升高而减小。由此说明左侧窗上的声源激励,主要成分是湍流压力脉动,其占比随频率增大而减小,但始终维持在一个较高的水平。
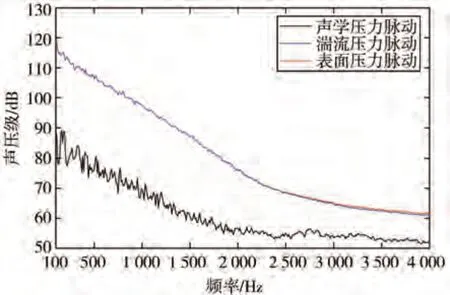
图19 左侧窗表面压力分解结果
3.2.2 内部噪声源项贡献度对比
图20为表面压力及不同压力脉动分别加载得到的内部噪声频谱图。由图可知,表面压力脉动产生的内部噪声在低频段时,受声学压力脉动与湍流压力脉动的共同作用,随着频率的升高,声学压力脉动逐渐占据主导地位,湍流压力脉动的贡献越来越小。在2 500~4 000 Hz 内,表面压力脉动的频谱曲线基本与声学压力脉动产生的内部噪声一致。由此说明,内部测点的噪声主要来自声学压力脉动,其占比随频率的升高逐渐增加,在高频段内的内部噪声基本由声学压力脉动造成。
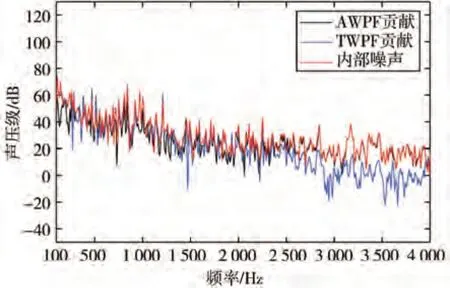
图20 内部噪声贡献对比图
3.2.3 传递效率对比
综上所述,声源激励和内部噪声的主成分完全相反,这是侧窗玻璃对不同声源激励的传递效率不同所致。
根据研究人员对板隔声量的研究发现,单层薄板在外部激励发生受迫振动时,会在板内产生弯曲波,当外部激励达到某频率时,弯曲波的波长在激励波方向上的投影等于激励波的波长,此时两种波发生共振,激励波以高传递效率通过薄板,这一现象被称为吻合效应。
由此可知,当声源激励的波数与弯曲波波数相近时,受激励引起的玻璃弯曲波波长与激励波波长接近,易引起共振,此时玻璃对该激励波的传递效率较高。为此,计算各频率下声源激励及侧窗玻璃波数之间的关系,公式如下:

式中:为湍流压力脉动的波数;为对流速度。

式中为声学压力脉动的波数。
式(3)表示湍流压力脉动对应波数与频率的关系。式(4)表示声学压力脉动对应波数与频率的关系。

上式表示玻璃受激励后产生的弯曲波波数,以无限大平板的波数求解公式进行近似求解。式中、、、分别表示玻璃的弹性模量、厚度、泊松比和密度。经计算得到如图21所示的波数-频率图。
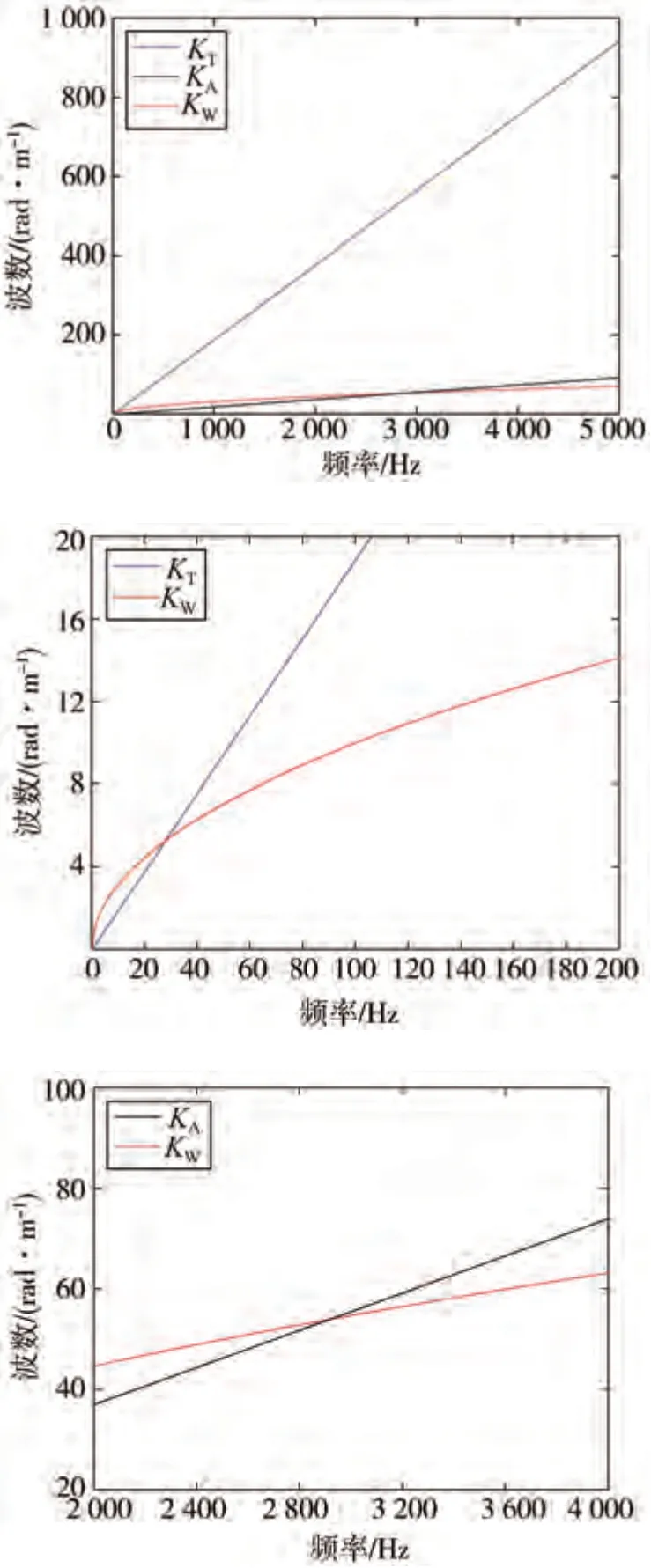
图21 声源激励及侧窗玻璃的波数-频率图
由图可知,全频段内声学压力脉动的波数与侧窗玻璃弯曲波的波数相近,即声学压力脉动在全频段上与玻璃弯曲波波长接近,因此声学压力脉动通过侧窗玻璃的传递效率较高,激励作用较明显。而湍流压力脉动的波数只在低频段内较为接近,在耦合频率以上,波数与弯曲波相差甚远,即湍流压力脉动仅在低频段内与弯曲波波长相近,因此湍流压力脉动通过侧窗玻璃的传递效率随频率升高而降低,激励作用并不明显。正是这样的传递效率差异导致了声源激励与内部噪声在主成分上完全相反的结果。
3.3 声场仿真结果验证
将声场仿真得到的频谱曲线与实验结果进行对比,如图22 所示。由图可知,实验与仿真结果的声压级随频率变化的趋势基本一致,除400~800 Hz外,各频率所对应的声压级在数值上差距较小。总的来说,实验与仿真整体一致性较好。其中400~800 Hz 的误差较其他频段明显,原因如1.3.2 节所述,该频段内不同NCT 的传递效率差异不足以忽略其他声源作用,因此产生仿真误差。综上所述,本文中采用的流场-声场联合仿真具有较高准确性。
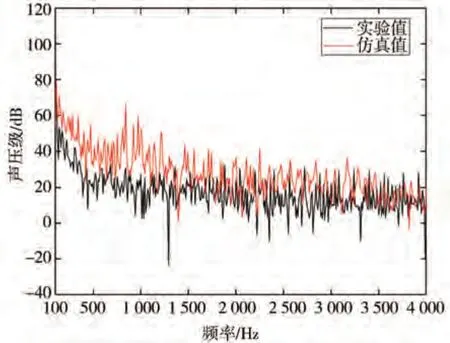
图22 内部噪声实验与仿真对比图
4 结论
基于HSM 标准模型的实验与仿真分析,得到如下结论。
(1)随风速增加,不同声源作用下的内部噪声在不同频段上变化规律不同。全铝窗、前玻璃窗和右侧玻璃窗作用下,声压级主要在1 200 Hz 以下随风速有明显变化,全玻璃窗和左侧玻璃窗作用下,声压级在全频段上随风速增加而增加,但增长幅度随频率增大而减小。
(2)模型前缘分离涡及其再附着引起的压力激励由各窗向内传递产生内部噪声,各窗对内部噪声的贡献大小为:左侧窗>右侧窗>前风窗。经实验验证,以左侧窗为唯一声源可获得与全部声源存在时相近的声压级结果,因此针对驾驶员左耳位置的噪声研究,可以只考虑左侧窗声源。
(3)表面压力激励包含湍流压力脉动和声学压力脉动,湍流压力脉动是声源激励的主成分,占比随频率升高而降低。声学压力脉动是内部噪声的主成分,占比随频率升高而增大。两者的差异是由玻璃对两种声源的传递效率不同引起的,这是不同激励与玻璃弯曲波之间不同波数关系导致的。
