钢纤维橡胶混凝土的循环受压应力-应变关系
2022-09-04赵秋红
赵秋红,董 硕,朱 涵,2,于 泳
(1.天津大学建筑工程学院,天津 300072;2.天津大学滨海土木工程结构与安全教育部重点实验室,天津 300350;3.青岛理工大学土木工程学院,山东 青岛 266033)
将橡胶和钢纤维共同掺入混凝土中来制备钢纤维橡胶混凝土(SFR-RuC),具有良好的延性、韧性、抗裂性和耐损伤能力[1-7].Karimipour等[3]发现与橡胶混凝土相比,SFR-RuC的抗压、劈裂抗拉及抗弯强度均有显著提高.Li等[4]和Noaman等[5]发现,受压时SFR-RuC中钢纤维的桥联拉结及橡胶的增韧抗裂作用能够得到充分发挥,显著提高混凝土的抗压韧性.Fu等[6]研究了SFR-RuC的断裂韧性,发现橡胶和钢纤维分别在初始裂缝和不稳定裂缝发展阶段起作用,协同增强其断裂韧性.但是,橡胶颗粒的掺入导致SFR-RuC的抗压强度显著降低[7].因此,为了将SFR-RuC更广泛地应用于结构工程中,有必要对其抗压强度进行优化控制.
混凝土的循环力学行为对其结构抗震性研究具有重要意义.普通混凝土[8-9]和纤维混凝土[10-13]的单轴受压循环力学行为已经得到了研究,并建立了相应的循环本构关系模型,对于SFR-RuC单轴循环受压力学行为的研究则尚未见报道.
本文通过配合比优化设计来制备与普通C60混凝土等强的SFR-RuC,并对不同橡胶及钢纤维掺量的SFR-RuC试件进行单轴循环受压应力-应变全曲线试验,分析橡胶及钢纤维对其循环受压力学性能的影响,建立SFR-RuC单轴循环受压应力-应变关系模型,为其在结构工程的应用提供一定的理论基础.
1 试验
1.1 原材料
水泥(C)为P·O 42.5普通硅酸盐水泥;粗骨料(CA)为粒径5~20 mm的连续级配碎石;细骨料(FA)为细度模数2.64的连续级配中砂;外加剂(SP)为减水率(质量分数)25%~35%的聚羧酸高性能减水剂;钢纤维(SF)采用端钩型钢纤维,长30 mm,等效直径0.75 mm,长径比40,平均抗拉强度不低于1 000 MPa;拌和水(W)为自来水;橡胶颗粒(R)由废旧轮胎经过机械破碎、筛分、清洗、除尘等流程制得,粒度1.00 mm,密度为1 050 kg/m3.
1.2 试件设计
为研究SFR-RuC单轴循环受压应力-应变全过程的力学行为,本文以橡胶颗粒和钢纤维掺量为变量,设计了12组试件.其中,钢纤维掺量Vf(体积分数,下同)分别为0%、0.5%、1.0%、1.5%,橡胶颗粒掺量ρr(体积分数,等体积替代砂)分别为0%、5.0%、10.0%、15.0%、20.0%.首先,设计强度等级为C60的普通混凝土(NC)试件;然后,加入预定掺量的橡胶颗粒,以轴心抗压强度达到40~50 MPa为目标,通过降低水胶比来进行配合比优化设计,得到等强橡胶混凝土(RuC)试件;最后,加入预定掺量的钢纤维,得到SFR-RuC试件.混凝土配合比及主要性能见表1.其中,R代表橡胶,F代表钢纤维,之后数字代表相应的掺量,如R10F1代表掺加10.0%橡胶颗粒、1.0%钢纤维的钢纤维橡胶混凝土,εc为峰值应变,Ec为弹性模量.由于钢纤维长度在40 mm以内,按照CECS 13—2009《纤维混凝土试验方法标准》,可采用尺寸为100 mm×100 mm×100 mm的立方体试件以及尺寸为100 mm×100mm×300 mm的棱柱体试件,并考虑尺寸效应乘以强度转换系数0.90.每组配合比均制作9个试件,其中3个立方体试件用于测量抗压强度(fc),3个棱柱体试件用于测量轴心抗压强度(fcu)以确定预加载标准,另外3个棱柱体试件用于测量单轴循环受压应力-应变(σ-ε)曲线.
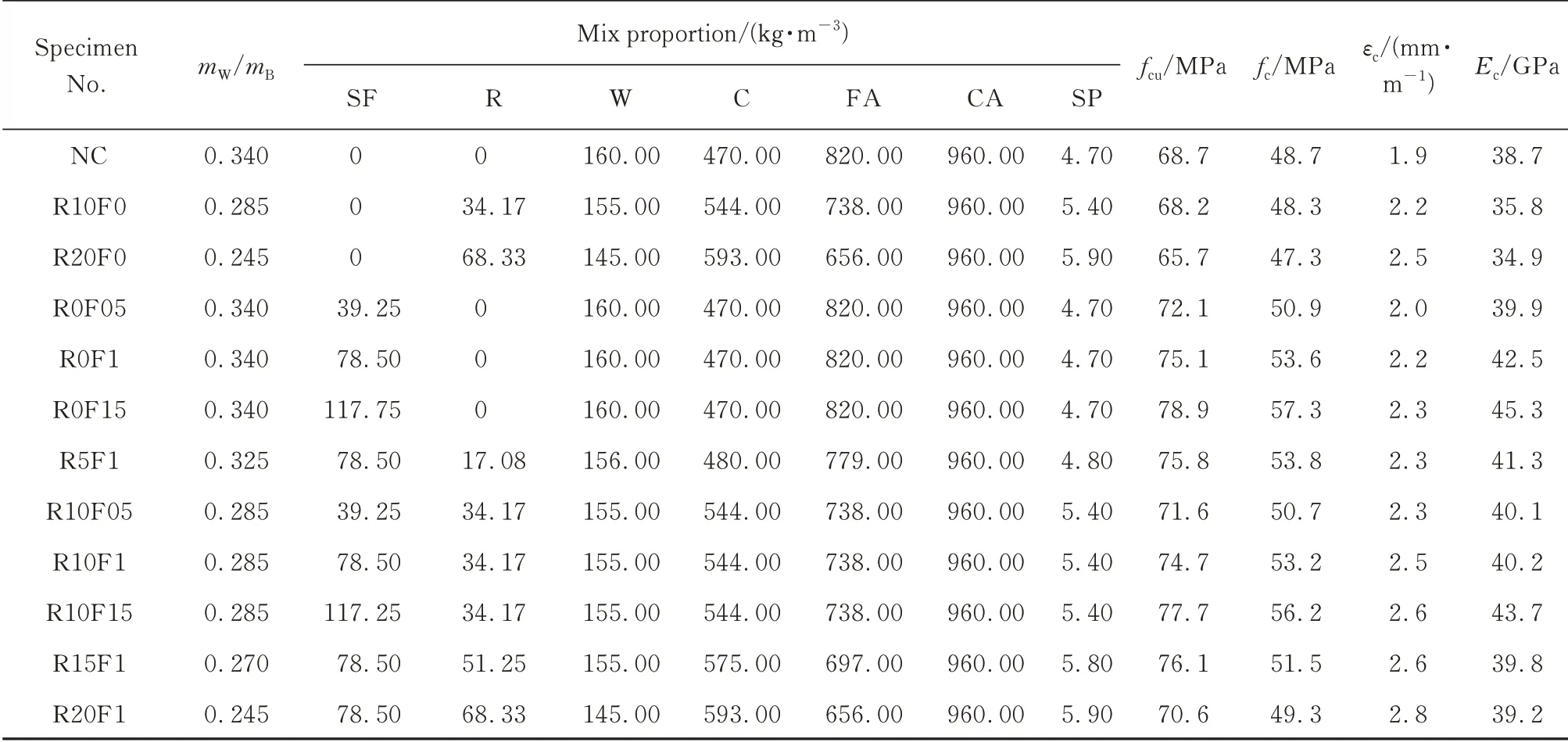
表1 混凝土的配合比及主要性能Table 1 Mix proportions and main properties of concretes
1.3 试验加载装置及测点布置
采用YAW-5000A型微机控制电液伺服压力机(可施加最大荷载为5 000 k N)对棱柱体试件施加循环轴压荷载,可实现精度为1%的闭环控制加载,内置Wintest数据采集系统以获得试件所受轴压荷载;试件中部安装WTB-100型引伸计,量测标距为100 mm,精度为1/1 000 000,外接静态数据采集系统以获得试件的压应变;为保证数据的同步检测,将2个数据采集系统的采集频率调整为一致,并在加载板下对称设置2个精度为0.01 mm的位移计,以监测轴向位移,如图1所示.首先对试件预加载至同组试件轴心抗压强度的10%,然后开始循环加载试验.试验加载采用位移控制模式,加载速率为0.005 mm/s,每级位移增量为0.24 mm,应变增量Δε=0.8×10-3;卸载采用力控制模式,加载速率为10 kN/s[9].

图1 试验加载及测量装置Fig.1 T est setup and instrumentation
2 结果及分析
2.1 循环受压全过程及破坏形态
图2为SFR-RuC试件单轴循环受压全过程.由图2可见,SFR-RuC试件单轴循环受压曲线包括6个特征阶段及其他加卸载阶段,各阶段曲线特征及裂缝发展如下:

图2 SFR-RuC试件单轴循环受压全过程Fig.2 Uniaxial cyclic compressive process of SFR-RuC specimen
(1)弹性阶段OA.曲线呈线性,骨料、水泥基体及橡胶颗粒受压产生弹性变形,试件基本无裂缝.
(2)细观裂缝扩展阶段AB.曲线开始呈非线性,水泥基体在粗骨料周围形成初始裂缝,并发展成微裂缝.橡胶颗粒强度较低,周围易形成薄弱带,微裂缝开展更为细密,并对其起到一定阻裂作用.钢纤维的约束作用尚未开展,十分有限.
(3)宏观裂缝扩展阶段BC.曲线呈明显非线性直至峰值点,在循环压力作用下,部分微裂缝连通形成宏观裂缝,试件横向变形发展速率明显增大,表面出现肉眼可见的竖向短裂缝.横跨宏观裂缝的钢纤维开始拉结并约束裂缝的开展,峰值应变显著增大.橡胶颗粒导致基体内部裂缝更为细密,形成多缝开裂,使得更多钢纤维横跨宏观裂缝,有效拉结裂缝及约束其开展.
(4)断裂发生阶段CD.曲线开始下降,D点应力约为峰值应力的90%.宏观裂缝进一步扩展延伸,试件表面出现多条不连续竖向短裂缝,沿对角线平行分布,交结形成主裂缝.钢纤维进一步有效约束宏观裂缝的发展和延伸.
(5)持续破坏阶段DE.曲线持续下降,E点应力约为峰值应力的60%~75%.主裂缝逐渐联结,斜向扩展成为斜裂面.斜裂面的抗剪及变形能力主要由钢纤维提供.
(6)收敛阶段EF.曲线下降趋于平缓,斜裂面持续变宽,发展延伸形成裂缝破坏带.在循环压力作用下,斜裂面上的混凝土受到挤压而剥落,拉结的钢纤维逐渐被拔出并发出声响.
(7)卸载阶段GH.曲线下降至零,横跨主裂缝的钢纤维拉应力降低,弹性变形恢复,裂缝宽度减小.
(8)再加载第1阶段HI.曲线再次上升至卸载时的应变,但无法达到卸载时的应力,裂缝宽度基本与卸载时相同.再加载第2阶段IJ,曲线继续发展至下一级卸载应变,裂缝宽度增加且数量增多.
图3为SFR-RuC试件断裂面的微观形态.由图3可见:橡胶颗粒与水泥基体之间存在明显的裂隙,界面过渡区的水化产物较少,其黏结及密实度较差,存在较大空隙,形成基体内的受力薄弱区,为多缝开裂的产生提供了条件;钢纤维与基体的裂隙细小,黏结密实度较高,使其在裂缝开展时能够更好地起到拉结作用.

图3 SFR-RuC试件断裂面的微观形态Fig.3 Micro morphology of fracture surface of SFR-RuC specimens
图4为12组试件的循环受压破坏形态.由图4可见:

图4 12组试件的循环受压破坏形态Fig.4 Cyclic compressive failure modes of twelve groups of specimen
(1)普通混凝土试件呈现明显的脆性破坏特征,裂缝穿过粗骨料形成断裂面,完全破碎;橡胶混凝土试件破坏形态较为完整,裂缝从加载端附近往下扩展汇聚成主裂缝;橡胶掺量越大,裂缝越细密,分布越均匀;钢纤维混凝土试件表面有明显的斜向裂缝带,纤维掺量增加时裂缝宽度减小.
(2)当SFR-RuC试件的橡胶掺量在10.0%以下时,表面也形成斜向裂缝带,与钢纤维混凝土试件相比,其裂缝更细密,分布更均匀;当橡胶掺量大于10.0%时,SFR-RuC试件表面出现细密裂缝,与橡胶混凝土试件更为相似.
2.2 循环受压应力-应变全曲线
图5为试件的单轴循环受压应力-应变全曲线.由图5可见:橡胶和钢纤维的掺入对混凝土的单轴循环受压力学行为,尤其是后期循环的影响明显,显著增加了试件的延性及耗能能力;与普通混凝土、橡胶混凝土及钢纤维混凝土试件相比,在橡胶自身耗能阻裂机制和钢纤维拉结耗能机制的共同作用下,SFR-RuC试件的塑性变形及延性更高,滞回环面积明显增加.
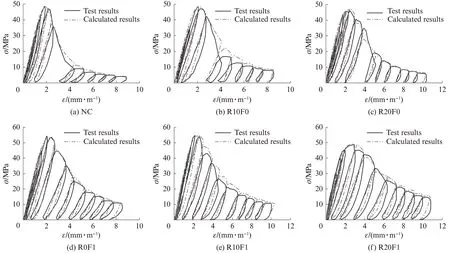
图5 试件的单轴循环受压应力-应变全曲线Fig.5 Uniaxial cyclic compressive stress-strain curves of specimens
图6为试件的循环受压全曲线包络线.由图6和表1可见:
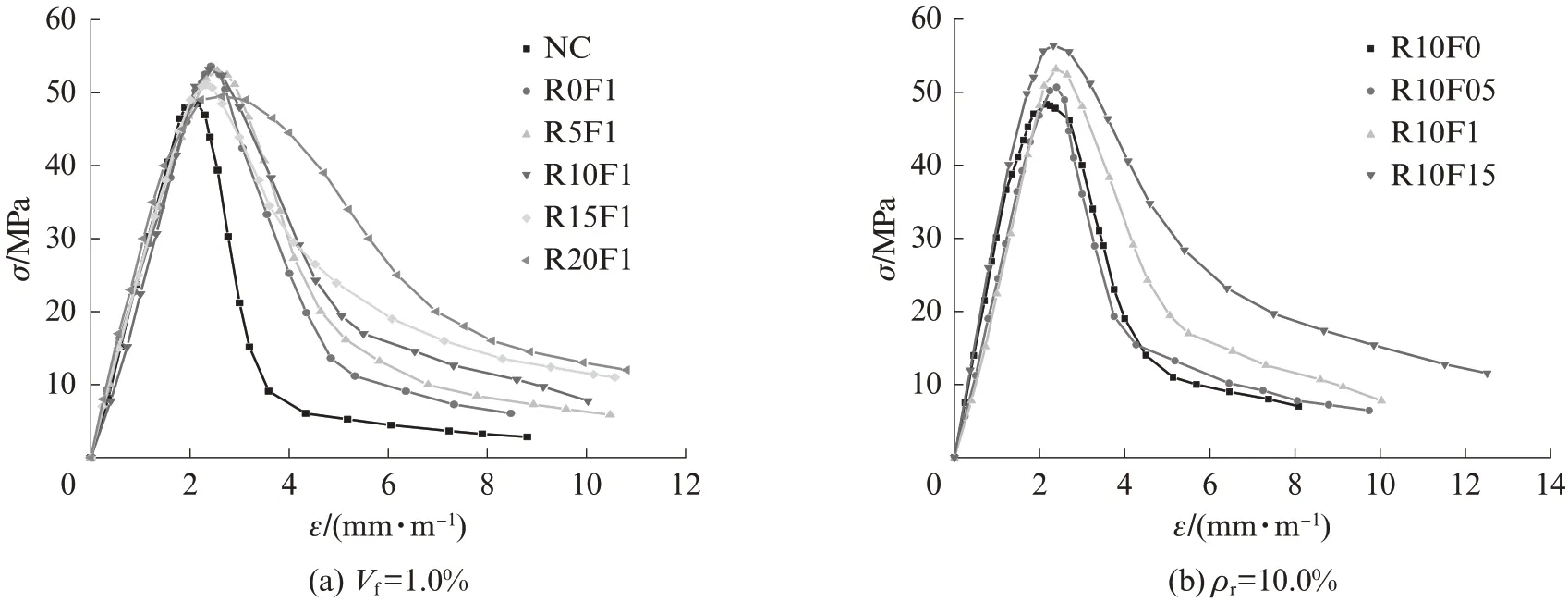
图6 试件的循环受压全曲线包络线Fig.6 Envelope curves of the cyclic compressive curves of specimens
(1)当钢纤维掺量不变、橡胶掺量增加时,包络线下的面积明显增加,而峰值应力几乎不变.表明通过配合比优化设计,成功克服了橡胶掺入对SFR-RuC抗压强度的削弱,使材料在橡胶掺量高达20.0%时仍能与C60混凝土基本等强,且耗能能力明显提高,适宜应用于结构抗震.
(2)当橡胶掺量不变、钢纤维掺量增加时,试件的抗压强度及耗能能力均有所提高,钢纤维掺量由0%增至1.5%时,抗压强度提高了16%,这是由于更多钢纤维参与到抵抗裂缝开展及拉结耗能的过程中.
2.3 刚度退化率
图7为试件刚度退化率与卸载点应变的关系.图中εeu为卸载点应变,Eeu/Ec为刚度退化率,Eeu为卸载刚度,定义为循环受压应力-应变全曲线的卸载点与相应塑性应变点所连直线的斜率[9](见图2).由图7可见:SFR-RuC的刚度退化率Eeu/Ec在循环加载前期随着卸载应变的增加明显下降,尤其是在到达峰值点之前,之后下降趋势明显变缓;与普通混凝土相比,掺入橡胶或钢纤维均使得材料的刚度退化率增加,即刚度退化变得更为缓慢,这种趋势在循环加载后期随着橡胶或者钢纤维掺量的增加更为明显.
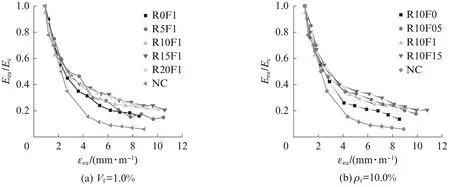
图7 试件刚度退化率与卸载点应变的关系Fig.7 Relationship between stiffness degradation ratio and unloading strain of specimens
2.4 塑性应变
图8为试件塑性应变与卸载点应变的关系.图中εeu/εc为标准化卸载点应变,εeu为卸载点应变;εp/εc为标准化塑性应变,εp为塑性应变,定义为试件在循环轴压荷载作用下,卸载至应力为零时相应的残余应变[11](见图2).由图8可见:塑性应变随着卸载点应变的增加而增加,在εeu/εc≤2时增加更快,之后基本呈线性增加的趋势.橡胶掺量的增加对塑性应变几乎无影响,但加载后期随着钢纤维掺量的增加,塑性应变有所降低,这是由于该阶段钢纤维的拉结作用开始充分发挥,减小了混凝土的塑性应变累积.因此,本文以分段函数的形式来描述SFR-RuC在单轴循环受压时塑性应变与卸载点应变的关系,如式(1)所示.当εeu/εc≤2时采用幂函数[11]的形式,在试验数据的基础上拟合幂函数;当εeu/εc>2时采用线性函数的形式,并引入钢纤维特征参数λf,在试验数据的基础上将线性函数的控制参数γf、φf拟合为λf的线函数(见式(2)、(3)),所得曲线与试验数据的对比如图8所示.
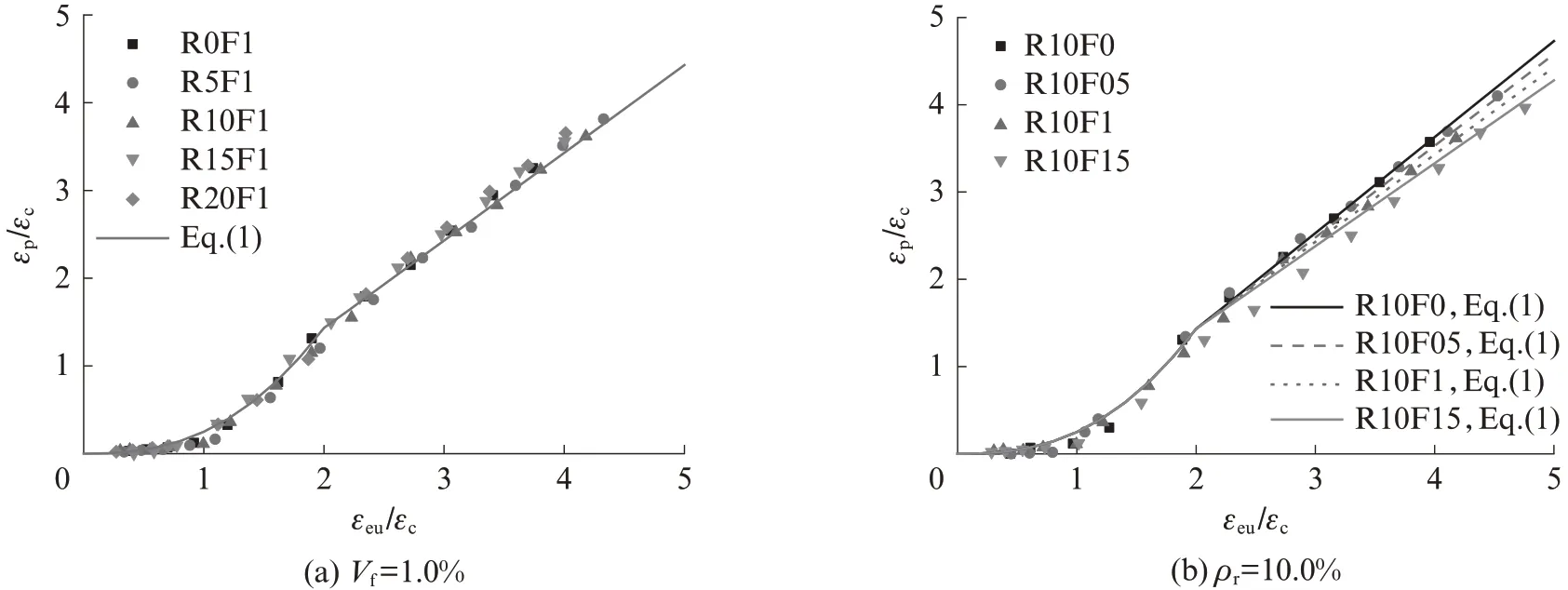
图8 试件塑性应变与卸载点应变的关系Fig.8 Relationship between plastic strain and unloading strain of specimens
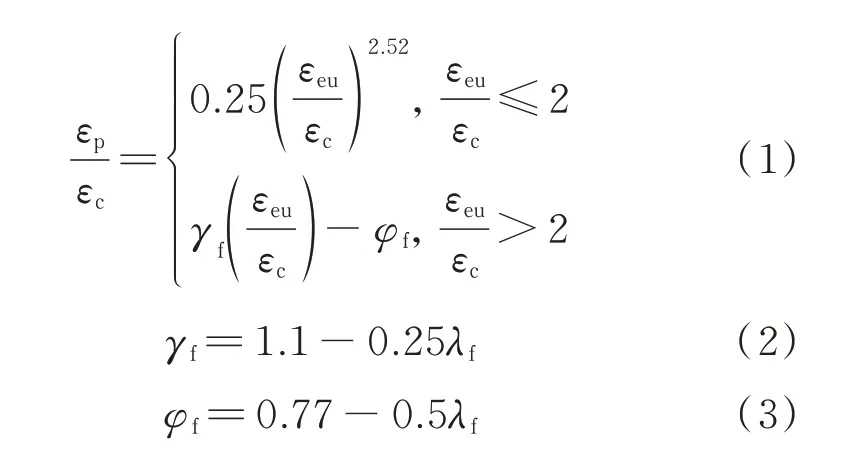
式中:γf、φf为考虑钢纤维影响的塑性应变控制参数;λf为钢纤维特征参数,λf=Vflf/df,其中Vf、lf、df为钢纤维体积分数、长度和等效直径,lf/df为长径比.
2.5 应力退化
由图5可见,SFR-RuC在单轴循环受压加卸载过程中存在应力退化现象,即再加载曲线接近包络线时其应力达不到上一级卸载应力.图9为试件应力退化率与卸载点应变的关系.图中εeu/εc为标准化卸载点应变,ξ=σre/σeu为应力退化率,其中σeu为卸载点应力,σre为转折点应力,定义为再加载曲线达到上一个循环卸载应变εeu时的应力[12](见图2).由图9可见,应力退化率随着卸载点应变的增加而降低,在εeu/εc>2时变化不再明显,且橡胶和钢纤维掺量对SFR-RuC应力退化率的影响无明显规律.因此,本文在试验数据的基础上,拟合出线性分段函数来描述应力退化率与卸载点应变的关系,如式(4)所示,所得曲线与试验数据的对比见图9.
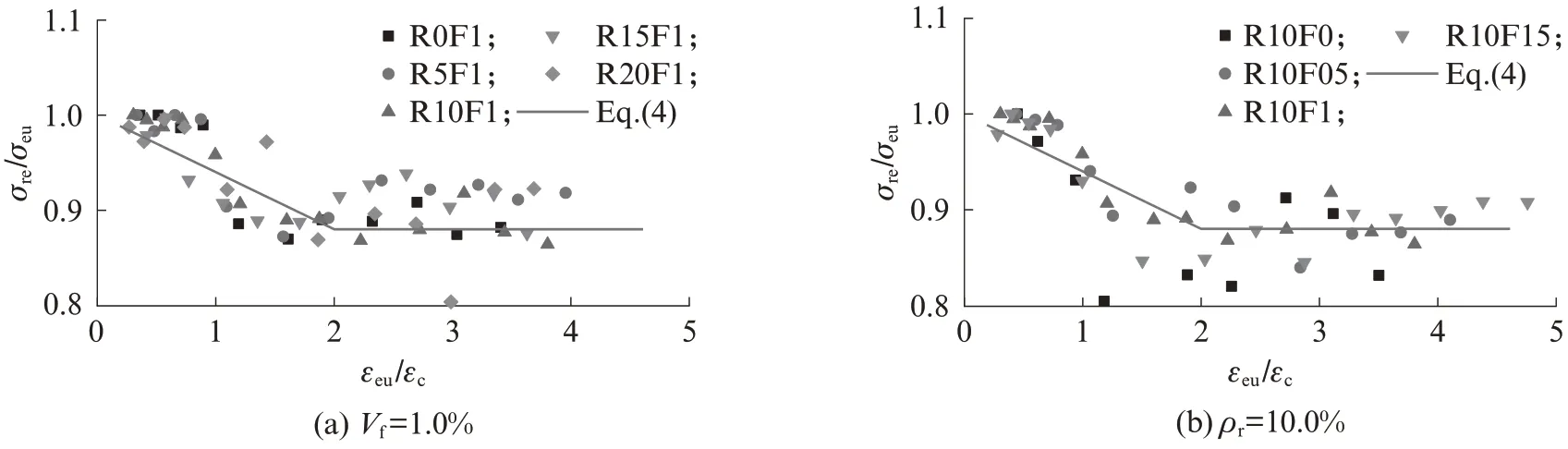
图9 试件应力退化率与卸载点应变的关系Fig.9 Relationship between stress degradation ratio and unloading strain of specimens

2.6 再加载曲线起点应变与终点应变关系
图10为试件再加载曲线的起点应变与终点应变的关系.图中εp/εc为再加载曲线标准化起点应变,εret/εc为标准化终点应变,其中εp为再加载曲线起点应变即塑性应变,εret为再加载曲线终点应变.由图10可知,再加载曲线终点应变随起点应变的增加而增加,在εeu/εc≤1时增加更快,之后基本呈线性增加的趋势,且橡胶和钢纤维掺量对SFR-RuC再加载曲线终点应变的影响无明显规律.因此,本文提出以分段函数的形式来描述SFR-RuC在单轴循环受压时再加载曲线终点应变与起点应变的关系,当εeu/εc≤1时,根据试验数据拟合为幂函数的形式;当εeu/εc>1时,根据试验数据拟合为线性函数的形式,如式(5)所示.所得曲线与试验数据的对比见图10.
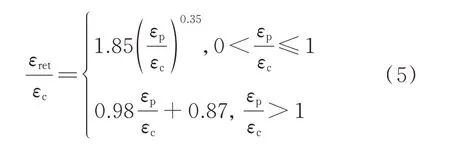
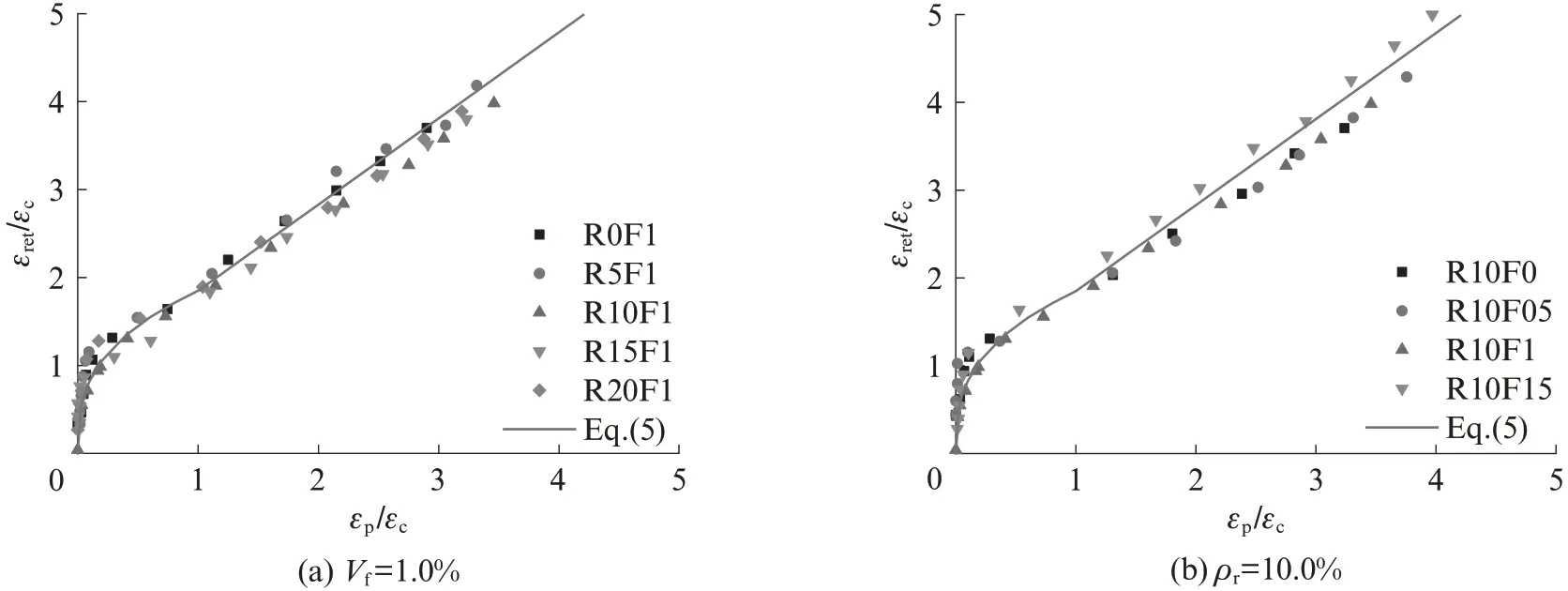
图10 试件再加载曲线的起点应变与终点应变的关系Fig.10 Relationship between ending point strain and starting point strain on reloading curve of specimens
3 循环应力-应变关系
3.1 循环应力-应变曲线包络线
已有研究表明,混凝土单轴循环受压应力-应变全曲线包络线的形状与混凝土单轴单调受压应力-应变全曲线大致相同[8,12],可采用损伤本构模型来描述.因此,本文采用GB 50010—2010《混凝土结构设计规范》的损伤本构模型来描述SFR-RuC单轴循环受压应力-应变全曲线的包络线,如式(6)~(12)所示.
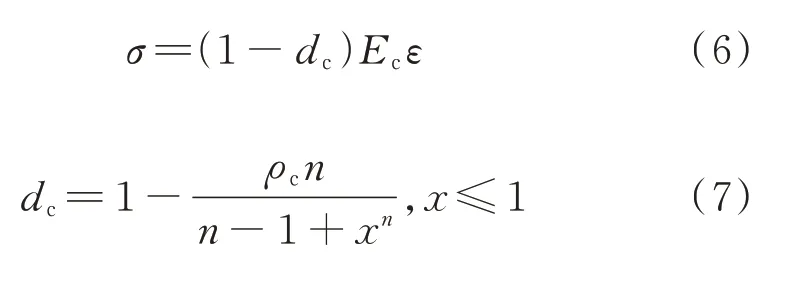
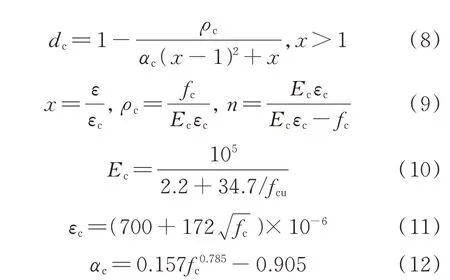
式中:dc为混凝土轴压损伤演化参数;αc为下降段形状参数.
考虑到橡胶与钢纤维的正向协同作用,在试验数据的基础上,本文分别采用钢纤维特征参数λf和橡胶特征参数λr对SFR-RuC的弹性模量Ec,fr、峰值应变εc,fr及下降段形状参数αc,fr进行拟合及修正,如式(13)~(16)所示.Ec,fr、εc,fr及αc,fr的计算值与单轴循环受压试验测得值的对比如表2所示.由表2可见,计算值与试验值吻合良好.
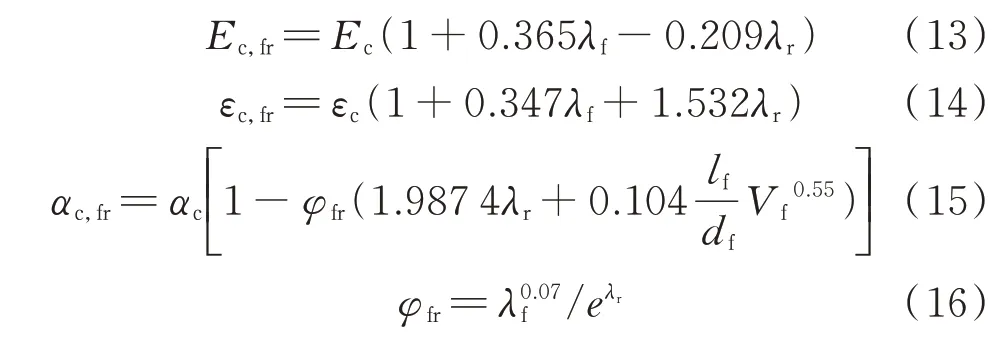
式中:λr为橡胶特征参数,λr=ρrdr,其中ρr、dr为橡胶颗粒等体积替换率和平均粒径;λf为钢纤维特征参数,λf=Vflf/df,其中Vf、lf、df为钢纤维体积分数、长度和等效直径,lf/df为长径比;φfr为同时考虑钢纤维和橡胶影响的下降段形状控制参数,当橡胶掺量或钢纤维掺量为0%时,φfr取为1.0.
3.2 卸载曲线和再加载曲线
在试验数据的基础上,采用幂函数的形式[8]拟合得到SFR-RuC单轴循环受压过程中卸载曲线的公式,如式(17)所示.

式中:a为卸载曲线参数,拟合取为1.0;mul为卸载曲率控制参数,根据试验数据拟合为标准化卸载点应变εeu/εc的幂函数:

由图2可见,再加载曲线在转折点εre前后的变化规律有所不同.在试验数据的基础上,采用分段函数的形式[8]拟合得到SFR-RuC再加载曲线的公式,如式(19)、(20)所示.
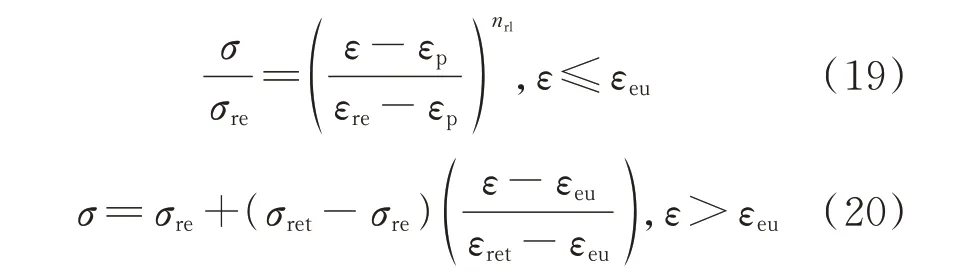
式中:nrl为再加载曲率控制参数,根据试验数据拟合为标准化塑性应变εp/εc的幂函数:

3.3 应力-应变关系验证
对已有文献中钢纤维混凝土的单轴循环受压应力-应变曲线[9]、非等强的橡胶混凝土和SFR-RuC的单轴单调受压应力-应变曲线[5]进行对比验证.图11为试件单轴循环受压应力-应变曲线计算值和试验值的比较.由图11可知,提出的模型能够较好地预测等强橡胶混凝土和SFR-RuC、钢纤维混凝土的单轴循环受压应力-应变全过程,但在预测非等强橡胶混凝土和SFR-RuC的单轴受压曲线下降段时,应力值偏大.这是由于通过配合比优化设计的等强SFR-RuC及橡胶混凝土克服了橡胶颗粒掺入对抗压强度的不利影响,同时保持峰值后延性较好.因此,考虑到材料的单轴循环受压应力-应变全过程会受到混凝土基体性能、橡胶颗粒及钢纤维特性等因素的影响,本文提出的模型适用于橡胶粒径为1 mm且等体积替代砂率0%~20.0%、钢纤维为端钩型长径比40且体积分数0%~1.5%、轴心抗压强度在40~50 MPa之间的等强SFR-RuC,具体使用时可根据实际试验数据进行调整.
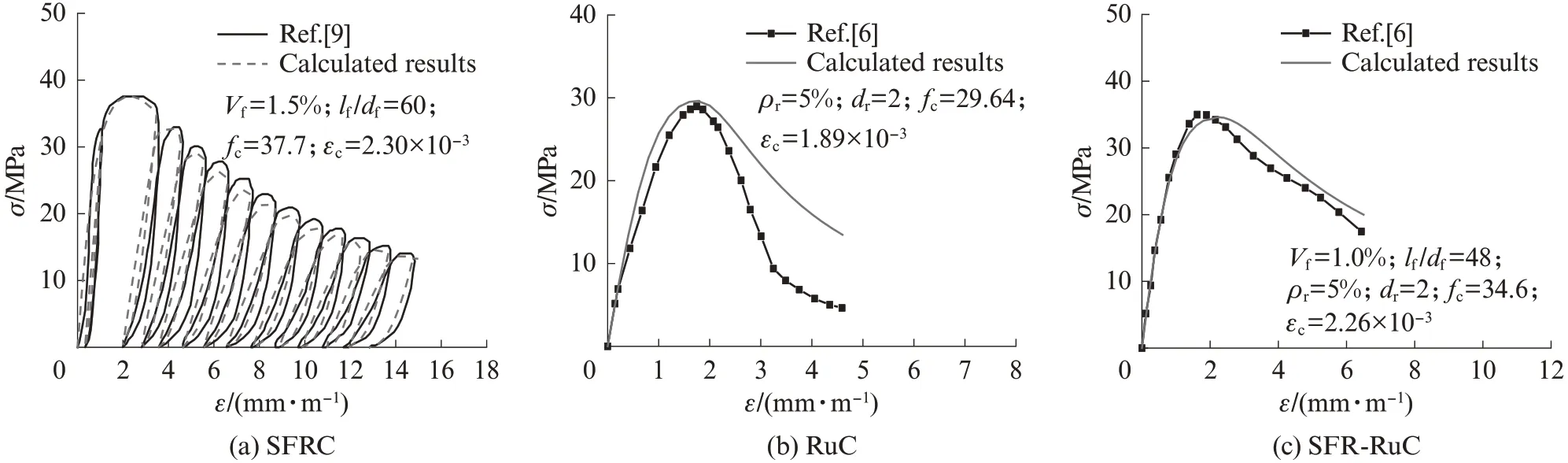
图11 试件单轴循环受压应力-应变曲线模型结果与试验结果的比较Fig.11 Comparisons between experimental and calculated results of cyclic compressive stress-strain curves of specimens
4 结论
(1)钢纤维的掺入可以显著改善橡胶混凝土的单轴循环受压力学性能,SFR-RuC试件的循环受压破坏呈明显延性特征,裂缝更为细密且完整性更好.与普通混凝土、橡胶混凝土及钢纤维混凝土试件相比,SFR-RuC试件的延性及韧性更高、滞回耗能能力增强,塑性应变累积及刚度退化更为缓慢.
(2)钢纤维与橡胶颗粒起到良好的协同作用,在循环加载初期,橡胶颗粒周围形成了薄弱带,使得微裂缝开展更为细密,更多钢纤维横跨于裂缝两侧;在循环加载后期,钢纤维有效桥接宏观裂缝,减小裂缝宽度并提供一定的变形能力,提高了材料的延性及耗能.
(3)通过配合比优化设计,成功克服了橡胶掺入对材料抗压强度削弱的缺点,SFR-RuC在橡胶掺量高达20.0%时仍能与C60混凝土基本等强,且耗能能力明显提高,适用于结构抗震中.
(4)在循环加载后期,随着橡胶和钢纤维掺量的增加,SFR-RuC的刚度退化更为缓慢,塑性应变降低,但橡胶和钢纤维掺量对于SFR-RuC的应力退化及再加载曲线的影响无明显规律.在试验数据的基础上提出了SFR-RuC塑性应变、应力退化及再加载曲线终点应变的分段函数模型.
(5)同时考虑橡胶和钢纤维的影响,提出了等强SFR-RuC的单轴循环受压应力-应变关系模型,以及卸载和再加载曲线的计算公式.模型计算值与本文及文献中的试验结果吻合较好,在具体使用时可以根据实际试验数据进行调整.
