基于深度学习的平面位姿估计算法
2022-09-04陈玉鹏
许 鲜,陈 宁,陈玉鹏
(集美大学海洋装备与机械工程学院,福建 厦门 361021)
0 引言
随着计算机视觉技术的发展,平面位姿估计在机器人技术、增强现实和虚拟现实、船舶海上作业等领域的应用越来越广泛[1-5]。尽管在过去几十年中,已经出现了很多平面位姿估计的方法,但是在快速准确和适应性方面还有很大的提升空间,尤其是对缺少纹理表面的平面目标而言。
平面位姿估计的目的是检测平面并估计其平移和旋转。传统视觉平面位姿估计通常分为两类。1)基于特征的方法[6-7],计算一组三维点和二维投影之间的对应关系,得到相机与平面之间的相对位置和方向,比如通过在平面物体上添加特定标志物,使用相机对特定标志物进行定位和检测,实现检测非接触式的平面位姿检测,其中比较成熟的方法有Aruco[8],Apriltag[9]等。然而这些方法精度易受场景限制,依赖于特定的特征,这些特征对图像变化和遮挡对不确定因素等的鲁棒性较差。2)基于模板匹配的直接方法[10],将姿态估计问题简化为模板匹配问题,通过优化参数来估计姿态,观察目标图像的刚性变换,但是这些模板匹配方法的主要缺点是,当仿射或者单应变换空间与姿态空间之间未对准时,容易产生额外的附加姿态误差。
随着深度学习对场景理解能力的增强,基于深度学习的位姿估计方法实现了精度、实时性和鲁棒性更好的位姿估计结果。Rad等[11]提出BB8网络,从单张RGB图像预测目标3D边框的2D投影,并使用PnP算法解算出目标3D位姿;Kehl等[12]提出了SSD-6D网络,使用合成数据集进行训练,将SSD用于三维实例检测和6D位姿估计,获得更好的实时性;Xiang等[13]提出PoseCNN网络,可以在杂乱场景中实现精确的物体6D姿态估计;Sida等[14]提出PVNet网络,从单张RGB图像预测目标的语义分割和物体关键点的向量场,使用随机投票算法计算出目标的关键点,并使用PnP算法解算出目标6D位姿;Chen等[15]提出DenseFusion网络,在像素级别嵌入和融合颜色和深度信息,以估计RGB-D图像中已知物体的6D位姿。然而现有大多数基于深度学习的位姿估计方法需要已知目标的三维模型,且网络的泛化性较差,很难实现未知模型的平面位姿估计。
最近的一些使用深度学习的平面重建方法可以从单幅RGB图像中检测平面实例分割、深度及法线信息。Liu等[16]提出了一种端到端的深度神经网络PlaneNet,从单幅RGB图像中推算平面参数及其对应的平面分割掩码;Yang等[17]提出一种针对室外场景的非监督学习方法PlaneRecover,预测平面实例分割及其平面参数。但PlaneNet和PlaneRecover两者都需要事先给出单个图像中的最大平面数,并且跨域的泛化能力较差。为了解决上述问题,Liu等[18]提出基于MaskRCNN的平面重建网络PlaneRCNN,可以从单个RGB图像中检测出小的平面区域并重建分段平面深度图;Yu等[19]提出了平面重建网络PlanarReconstruction,训练卷积神经网络得到每像素的嵌入映射,再使用聚类算法对嵌入向量分组得到任意数量的平面实例,通过平面参数预测分支得到平面参数。受这些工作的启发,本文使用基于深度学习的方法进行平面分割和法线估计,并经过位姿解算实现单个RGB图像的平面位姿估计,解决传统视觉位姿估计需要添加特定标志物和现有深度学习位姿估计算法需要已知物体三维模型的问题。
1 平面位姿估计试验系统
1.1 平面位姿估计试验系统硬件设计
基于实验需求搭建一套平面位姿估计实验系统,如图1所示,包括六自由度运动模拟系统和视觉检测系统。其中:六自由度运动模拟系统通过输入设定的运动方程模拟需要的六自由度运动;视觉检测系统通过相机可以获得其安装视野下的彩色RGB图像,通过单目视觉位姿检测算法检测出目标位姿,可对位姿估计效果进行验证。

1.2 基于深度学习的单图像位姿估计算法
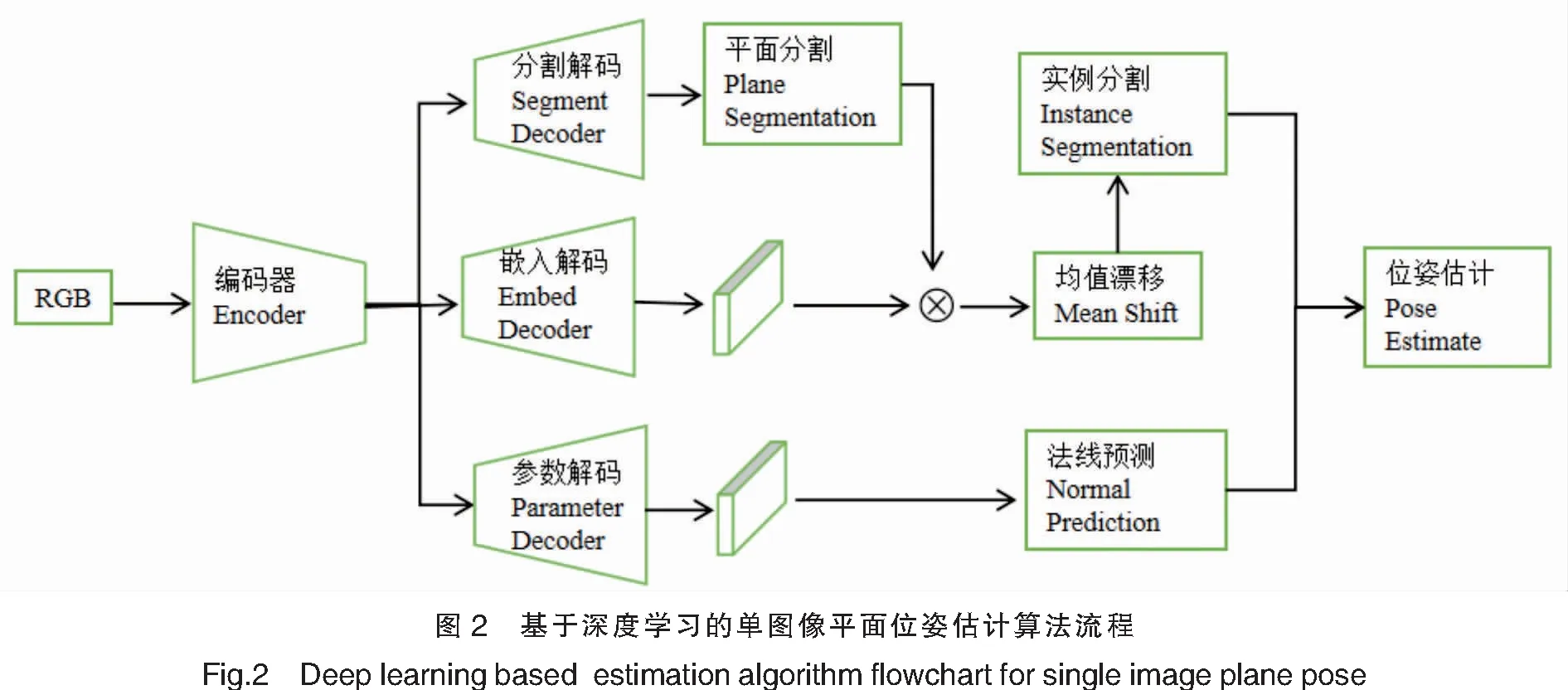
本文的目标是从单个RGB图像推断平面实例和平面位姿,算法框架如图2所示。在第一个阶段,使用多分枝的编码器-解码器网络共同预测单图像平面实例和法线。基于ScanNet[20]数据集生成平面实例数据集,并进行训练,输入单张RGB图像,采用编码器-解码器网络获得每个像素的关联嵌入向量,使用均值漂移算法对嵌入向量进行聚类,得到平面实例分割;共享编码特征进行平面参数分支解码,得到每个像素的法线信息。第二个阶段,对获得的平面掩码和法线进行位姿解算,获得平面的位姿,对实例分割和法线进行位姿解算,得到每个平面实例的位姿信息,最后通过实验对基于深度学习的平面位姿估计算法的可行性进行验证。
2 原理及方法
2.1 数据集构建
用于平面位姿估计的深度学习算法需要大量数据集进行训练,同时平面区域在图像中可能具有复杂的边界,手动标注这些区域非常耗时,并且不能保证对数据集提供精确的位姿标注。为了避免繁琐的手动标注过程,可以使用模型拟合算法,将现有RGB-D数据集中的每像素深度图转换为平面实例标注,使用PlaneNet生成的ScanNet数据集[20]训练并评估该方法,通过将平面拟合到ScanNet的合并网格并将其投影回各个框架,可以获取真实值。生成过程还包含来自ScanNet的语义注释,结果数据集包含50 000个训练图像和760张测试图像,分辨率为256 px×192 px,数据集含有深度信息,并具有平面实例分割标记及平面法线信息。
2.2 算法网络结构
平面位姿估计算法采用一种编码器-解码器的网络结构,如图3所示。
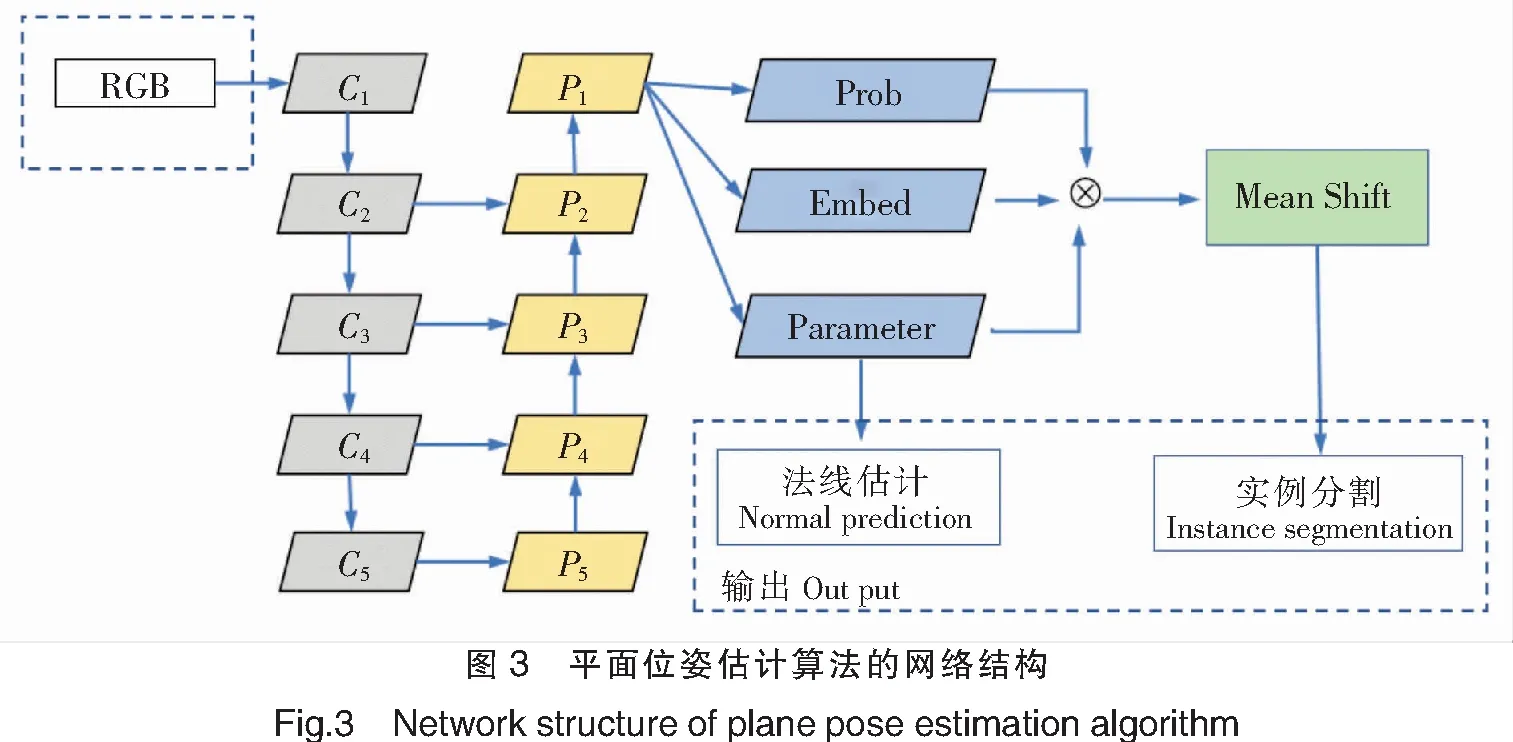
其中:C为卷积层;P为池化层。输入单张RGB图像,编码器使用ResNet101-FPN网络,解码器分别为平面/非平面语义分割,关联嵌入向量和平面参数解码,三个分支共享相同的高级特征映射。C1~C5采用自下向上的通路,即普通卷积特征自底向上逐层浓缩表达特征的过程。此过程低层表达边缘等较浅层次的图片信息特征,较高层表达较深层次的图片特征,如物体轮廓、类别等。P1~P5采用自上至下的通路,处理每一层信息时会参考上一层的高维信息作为输入。上层特征输出的特征图尺寸小但感受野更大,高维信息经实验证实能够对后续的目标检测、物体分类等任务发挥关键作用。解码器网络采用1×1卷积,可有效降低中间层次的通道数量,使输出不同维度的各个特征图有相同的通道数量。平面参数解码分支得到法线估计结果,结合平面/非平面语义分割和平面参数解码,使用均值漂移聚类算法对嵌入向量解码进行聚类,得到平面实例分割结果。深度学习算法的网络输出为法线估计和实例分割。
2.3 损失函数
对平面/非平面分割解码器,由于平面/非平面分割区域在人为环境下不平衡,因此采用式(1)所示的平衡交叉熵损失函数。
(1)
其中:F和B分别是前景(平面)和后景(非平面)像素点集;pi是第i个像素属于前景的概率;ω是前景和后景像素点数的比值。
平面嵌入解码器采用关联嵌入的思想,为每个像素预测一个嵌入向量,采用式(2)中的判别损失函数,其中“拉”损失将每个嵌入拉到对应实例的平均嵌入,而“推”损失将实例中心彼此推开,使同一平面实例中的像素比不同平面中的像素更接近。由于图像中平面实例的数量不是先验已知的,采用均值漂移聚类算法将得到的嵌入向量分组成平面实例。标准均值漂移算法在每次迭代中对所有像素嵌入向量进行两两距离计算,计算复杂度较大。为了解决实时性,PlanarReconstruction在聚类开始时过滤掉局部密度较低的锚点,并提出了均值漂移聚类的一个快速版本,只移动嵌入空间中的少量锚点,并将每个像素分配给最近的锚点。聚类算法收敛后,形成聚类,每个聚类对应一个平面实例,聚类中心是这个聚类中锚点的平均值。
LE=Lpull+Lpush。
(2)
其中:
(3)
(4)
其中:C是标准的聚类(平面)的数量;NC是每个聚类中元素的数量;xi是像素嵌入;μc是聚类C的平均嵌入;δv和δd分别是拉损失和推损失边界。如果嵌入的像素是容易分离的,即类内实例的距离大于δd或嵌入向量及其中心之间的距离小于δv,惩罚是零,否则惩罚将大幅增加。
平面参数分支推断图像每个像素点的平面参数,即点的法向量,使用式(5)中的L1损失即L1范数损失函数,也被称为最小绝对值偏差,是目标值与估计的绝对差值的均值。
(5)
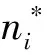
已知同一平面上单位法线相等且满足平面公式(6)。
nT·Q=1。
(6)
其中:n为平面法线,为单位法线矢量(M)除以平面偏距(d),即n=M/d;Q为平面像素点3维坐标。
由此先验知识,使用如式(7)所示损失函数,使同一平面实例上法线相等。
(7)
2.4 位姿解算
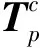
(8)
其中:α、β分别为绕x、y轴的转动角;[tx,ty,tz]T为平移矢量。
在相机坐标系中,平面公式满足式(9)。
nx·xc+ny·yc+nz·zc=1。
(9)
在理想针孔模型下,摄像机的成像模型齐次坐标投影关系为:
(10)
其中:fx,fy为焦距;cx,cy为图像中心与像素坐标系原点像素偏差;R,T分别为旋转矩阵和平移矩阵,M1,M2分别为摄像头的内参矩阵和外参矩阵;[uv]为像素坐标系下坐标点;[xcyczc]为相机坐标系下坐标点;[xwywzw]为世界坐标系下坐标点。
由式(10)和式(11)可得相机坐标系下坐标点为[xcyczc]。
(11)
联立两式解得:tx=x0;ty=y0;tz=z0;α=arcsin (ny);β=arctan(-nx/nz)。代入式(8)可解得M2,得到平面的位姿。
3 实验
首先对平面重建网络进行复现和对比,在此基础上选择泛化性更好的平面重建网络架构。然后使用选定的平面重建网络进行平面实例分割和法线估计,在ScanNet数据集上对平面实例分割和法线估计的结果进行量化分析和评估。最后在ScanNet数据集上对平面位姿估计的结果进行对比分析,并在NYU数据集和平面位姿估计实验系统上进行验证。使用PyTorch来实现本文的模型。服务器平台配置:Intel(R) Core(TM) i7-7700K CPU@4.2GHz处理器,16 GB内存,1T盘,8GB Geforce GTX 1070 GPU。
3.1 平面实例分割结果
平面重建网络PlaneRCNN和PlanarReconstruction均使用ScanNet数据集进行训练,并使用NYU数据集和用户图片对两者的训练结果进行测试,测后对比结果如图5所示。由图5可见,PlaneRCNN对小平面的检测结果较好,但会误识别多余的小平面。相比之下,PlanarReconstruction对小平面的检测效果较差,但能够检测出较完整的平面,该网络对平面实例的检测具有更好的泛化性。因此本文尝试在平面重建网络PlanarReconstruction基础上进行平面位姿估计。
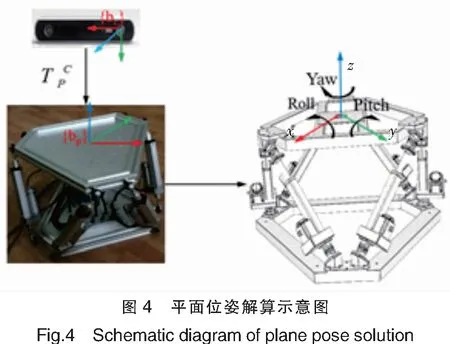
图6为在ScanNet数据集上的平面实例分割结果,与真实平面实例分割相比,基本能得到数量和形状一致的平面分割结果。平面召回率是正确预测标准平面的百分比,像素召回率是正确预测平面内像素的百分比,因此,本文使用平面和像素召回率作为评价指标。标准平面预测指标:ⅰ)其中一个预测平面交并比(IOU,Intersection over Union)得分大于0.5;ⅱ)重叠区域平均深度差小于阈值,该阈值从0.05 m到0.60 m不等,增量为0.05 m,则认为标准平面预测正确。实验中,通过该指标进行判定得到算法的平面和像素召回率,图7为在ScanNet测试数据集上的平面召回率(蓝色)和像素召回率(黑色),可以看出测试集上平面召回率平均值为0.625,像素召回率平均值为0.773。

3.2 平面位姿检测结果
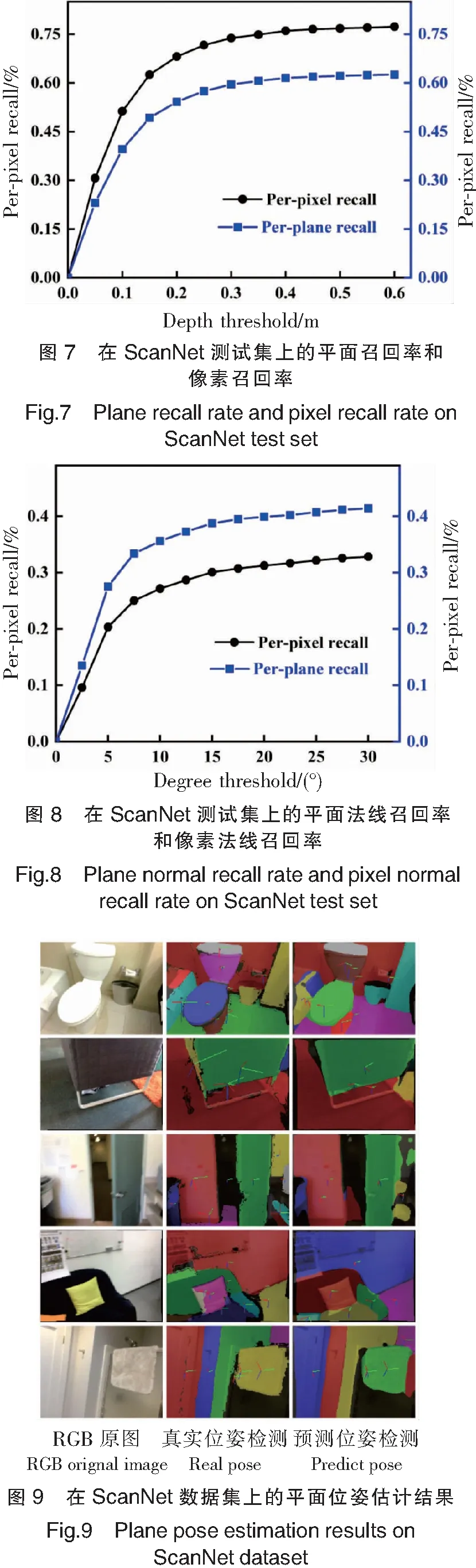
法线估计的准确性是平面位姿估计准确率的关键因素。根据研究,平面法线召回率是正确预测标准平面法线的百分比,像素召回率是正确预测法线的平面内像素的百分比。其中平面法线预测指标为:ⅰ)其中一个预测平面交并比(IOU)得分大于0.5;ⅱ)预测法线与真实法线夹角小于阈值,该阈值从0到30°不等,增量为2.5°,则认为平面法线预测正确。实验中,通过该指标进行判定,得到算法的平面和像素法线召回率。
如图8为在ScanNet测试数据集上的平面法线召回率(蓝色)和像素法线召回率(黑色),可以看出平面法线召回率平均值为0.414,像素法线召回率为0.328。
表1为在ScanNet测试数据集上的深度预测准确率,其均方根误差为0.039 m。由图8和表1可以看出,相比平面实例分割效果,基于单图像的平面法线预测精度还有较大提升空间。
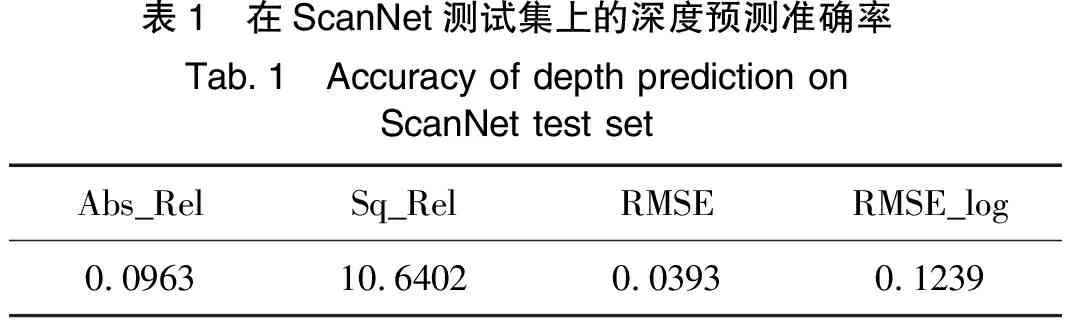
表1 在ScanNet测试集上的深度预测准确率Tab.1 Accuracy of depth prediction onScanNet test setAbs_RelSq_RelRMSERMSE_log0.096310.64020.03930.1239
使用位姿解算算法对平面实例分割和法线估计进行位姿解算,在ScanNet数据集上的平面位姿估计结果如图9所示。
其中:第2列为使用深度学习预测的平面实例分割和法线估计解算的平面位姿,第3列为使用数据集中真实平面实例分割和法线信息解算的平面位姿。图9中,每个平面实例中心处均标记解算得到的平面坐标系,红绿蓝颜色的坐标轴分别为x,y,z轴。本文采用的平面位姿估计计算法在简单场景下的位姿估计结果基本与真实值一致。
图10为在用户图片和NYU数据集上的平面位姿检测结果,可以看出位姿估计结果仍具有一定参考性。

实验中在ScanNet数据集上预测每张图片平面位姿平均用时0.0545 s,实时性为18.5 f/s,基本满足实时性要求。
4 结论
本文研究了基于深度学习的平面位姿检测算法,采用编码器-解码器网络从单个RGB图像中检测平面实例分割及法线信息,对每个平面进行位姿解算,从而获得其实时位姿。实验结果表明,在ScanNet测试数据集上的平面召回率为0.625,平面法线召回率为0.414,实时性为18.5 f/s。同样在NYU和用户自制的RGB图上平面分割效果较好,但基于单图像的平面法线预测准确率较差,平面位姿估计效果有待提高。同时还表明,基于深度学习的RGB图像平面位姿检测方法是可行的,但平面检测效果尤其是单图像法线和深度估计的准确率有待进一步提升。未来改进平面位姿检测的工作应该集中在研究更鲁棒的实例分割和法线估计算法,尝试多视图、多传感器融合等方法来提高平面位姿估计的准确率。
