星地双向时差测量系统周跳探测与修复算法

韩子彬，白燕，张峰，郭燕铭，卢晓春

( 1. 中国科学院国家授时中心, 西安 710600；2. 中国科学院精密导航定位与定时技术重点实验室, 西安 710600；3. 中国西安卫星测控中心, 西安 710043；4. 中国科学院大学, 北京 100049 )

0 引 言

目前常用的星地时间频率传递方法主要有双向时差测量及时间同步法、单向时间同步法、倒定位法以及激光测距法. 这些方法各有特点，其中双向时差测量及时间同步法可以实现较高的时间同步精度，吕宏春等[1]分析了星间链路体制下的双向时间同步精度，其1 h钟差拟合精度能够达到0.15 ns. 但以上基于伪码的双向时差测量仍无法满足对高精度的时间频率基准的应用. 载波相位测量相较于伪码测量具有更高的精度，张鹏飞等[2]分析了北斗卫星导航系统(BDS)下载波相位时间传递长基线链路精度可达0.2 ns，短基线链路精度可达0.02 ns. 针对更高的测量精度需求，将载波相位测量运用到双向时差测量及时间同步技术中，可以达到更高的时间同步精度. FONVILLE等[3]在载波相位双向时频传递模型下，实现了美国海军天文台(USNO)到德国联邦物理研究院(PTB)间10-12s量级的传递精度. 然而对于更加复杂的星地环境，由于航天器飞行动态高，时频传递链路的传输频率高，载波多普勒效应大，载波相位测量更容易出现粗差和周跳，双向时差测量中载波相位测量数据的可靠性不能完全保证，因而对载波相位周跳探测与修复技术[4-8]提出了更高的要求.

目前，国内外学者对周跳探测已经提出一些有效的方法，诸如电离层残差法(GF)[9-11]、多项式拟合法[12]、双频码相组合法[13-15]、高次差法[16]等，但是这些方法各有优劣，单独使用一种方法时存在不同的缺陷，因此诸多学者采用两种或两种以上的探测方法进行组合探测. 范士杰等[13]采用GF法和双频码相(MW) 组合法两种方法进行探测，并对两种方法进行了改进，利用时间窗口合理确定电离层残差法中的阈值大小，并将加权递推平滑和时间窗口结合估计宽巷模糊度，以此确定更合理的阈值；张小红等[14]对TurboEdit算法进行了改进，针对MW组合和GF组合构建了自适应的阈值模型，以提升探测精度；王成等[17]将码相观测量二次差分构建周跳检验参数，并引进了Jarque-Bera正态检验方法实现实时周跳探测.

本文针对高精度星地双向时间比对需求，提出一种适用于星地双向时差测量系统的周跳探测与修复方法，该方法联合MW组合法可以实现不同类型周跳的探测与修复. 通过搭建仿真实验平台对本文提出的周跳探测与修复方法进行实验验证，结果表明：对于上下行三条微波链路均可探测出周跳的存在并实现毫米级周跳修复精度，进一步对其星地时间同步性能进行分析，在经过周跳探测与修复，以及链路时延数据处理后，其星地时间同步精度优于0.3×10-12s.

1 星地双向时差测量系统实现原理

高精度星地双向时差测量系统采用基于载波相位测量的双向测量模式，具有单上行和双下行三条微波链路[18-20]，示意图如图1所示. 其中，上行链路fGS和下行链路fSG1可实现双向时差测量，三条链路组合可实现载波相位周跳探测与修复.

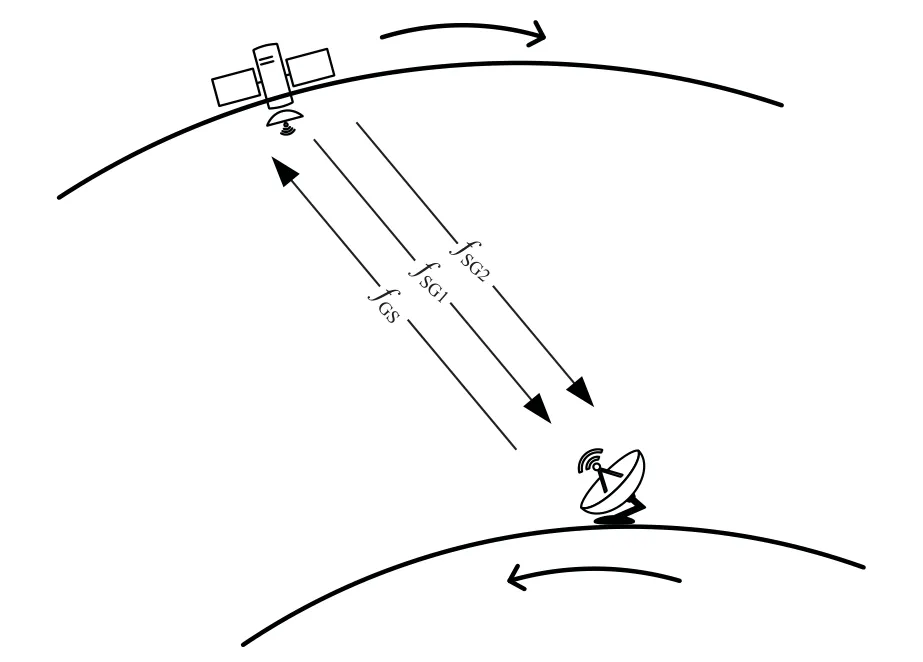
图 1 信号体制示意图

1.1 观测方程

在不考虑多路径效应的情况下，三条微波链路对应伪距观测方程表示为式(1)～(3)，载波相位观测方程表示为(4)～(6)：

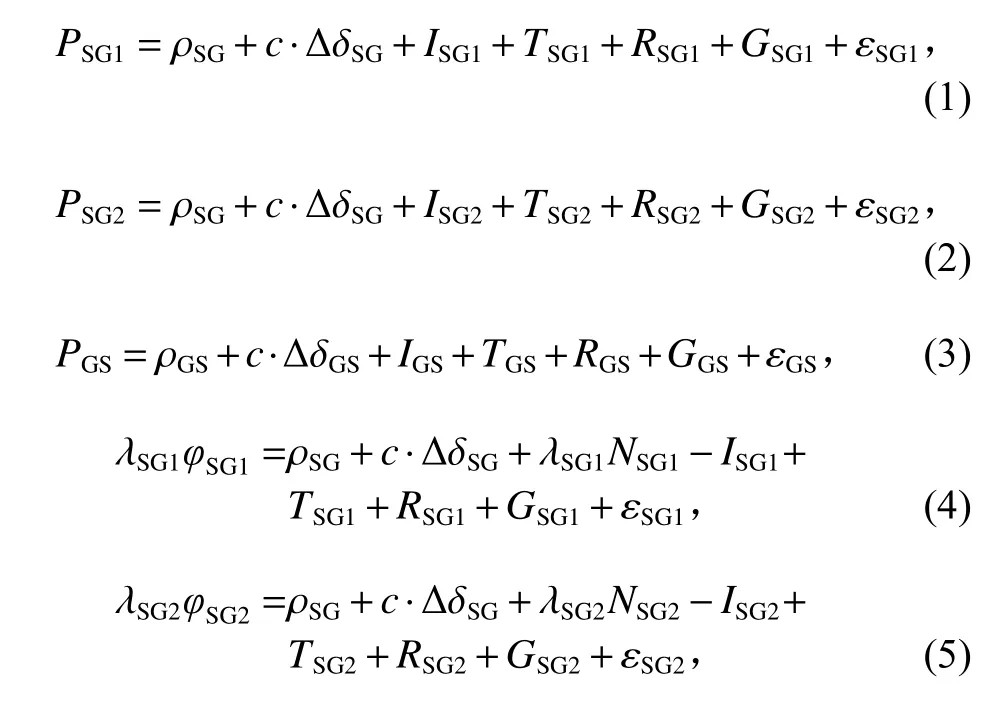
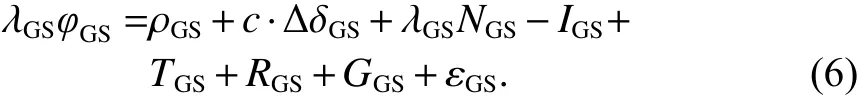
式中： S G1 、 S G2 和 G S 下标分别对应下行双频及上行单频微波链路；P为码伪距观测值；φ为载波相位观测值； λ 为载波波长； ρ 为卫星到地面站间的几何距离；Δδ 为星地间钟差；c为光速；N为整周模糊度；I为电离层误差；T为对流层误差；R为相对论引起的误差；G为引力时延误差； ε 为观测噪声.

1.2 基于载波相位的双向时差测量

与伪码的双向测量类似，根据载波相位的观测方程得到基于载波相位的双向时差测量方程，将上行链路fGS和下行链路fSG1对应相位伪距值作差得

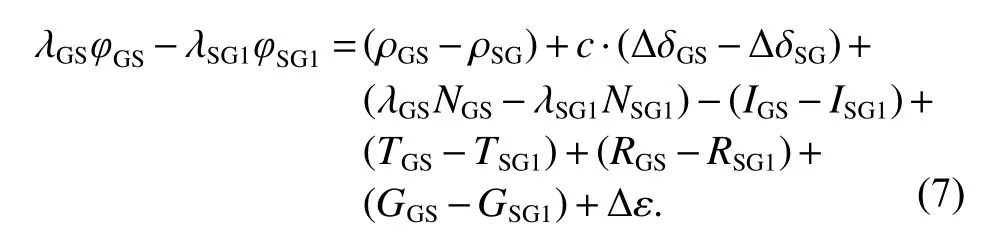
式中，星地钟差的关系为 Δ δ=ΔδGS=-ΔδSG，所以整理可以得到星地钟差为

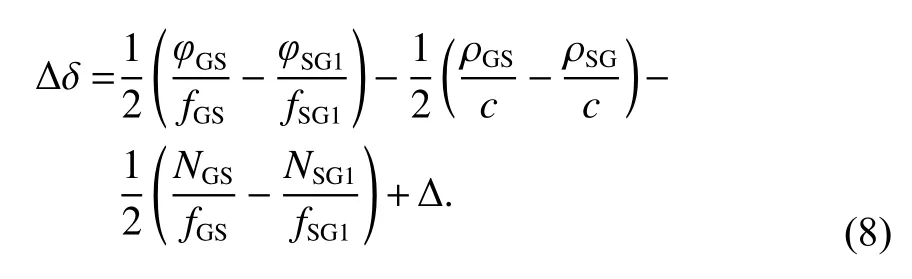
式中， Δ 包括由于路径不对称导致的电离层时延、对流层时延、相对论效应时延以及引力时延，这些误差在双向时差测量中是必须要考虑的，此类误差处理不是本文重点，且与周跳修复性能评估无关，这里不再过多赘述. 信号在空间的传输过程中，由于传输延迟和卫星的高速运动，星地双向伪距测量值中包含了不同时刻的卫星位置，为此需要将双向相位伪距中包含的时空信息归算至同一时刻[21].

由式(8)可知，上行链路fGS和下行链路fSG1若存在一个周期的周跳误差分别可以导致1.865 7×10-11以及1.644 7×10-11双向时间同步误差，显然实现高精度的周跳修复也是提升双向时间同步性能的关键因素.

2 周跳探测与修复方法

2.1 三频组合探测周跳

由于星上本地时间和地面站本地时间存在差异，即使上行与下行观测文件中的接收时间相同，其几何距离与钟差也不完全相同，所以不可以通过传统的周跳探测与修复方法进行分析，为融合上行与下行链路数据，先将双下行码伪距、载波相位伪距与对应上行伪距相减，得到作差后的组合观测方程：

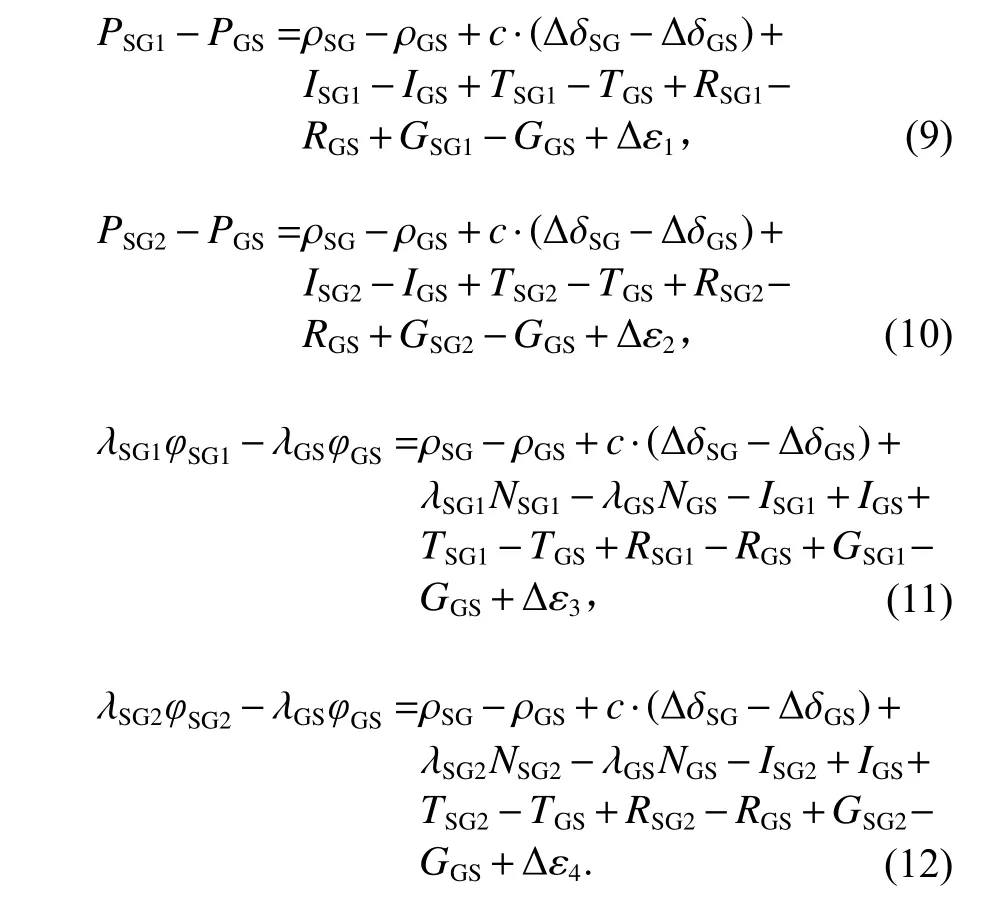
式中符号与前文所示一致，其中 Δ ε1、 Δ ε2、 Δ ε3和Δε4为观测噪声残差. 差分后的组合观测方程，伪码和相位间各式除电离层误差和整周模糊度外，其他各项保持一致，即在同一钟面时刻t，下行减上行的星地几何距离、星地间钟差、对流层误差是对应相等的，将相位减伪距便可得到只保留整周模糊度和残差的组合观测量：

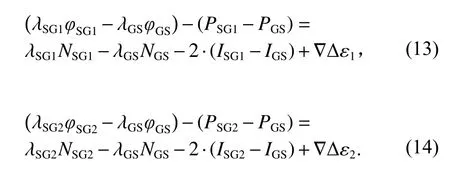
三频组合法消除星地几何距离、星地间钟差、对流层误差，只保留了电离层误差、模糊度以及观测噪声，非常适合用于探测周跳. 由于两个相邻的历元间电离层变化较小，对式(13)～(14)历元间作差，得到对应的检验量公式：

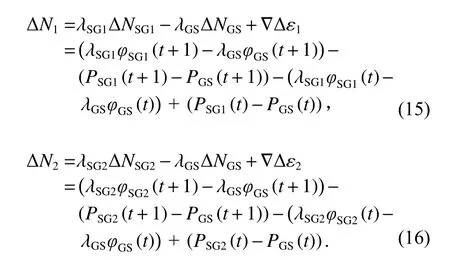
历元间求差后，无周跳情况下的组合序列将在“0”周围波动，发生周跳后，检验量则会超出探测阈值. 在无周跳情况下，影响检验量波动的量只有观测噪声，载波相位测量误差主要包括相位抖动和动态应力误差，经分析本文仿真系统中相位观测噪声在载噪比大于40 dB·Hz时，即可满足0.3×10-12s的测距误差，所以取 σφ=σφSG1=σφSG2=σφGS=0.01 即可满足系统要求，伪距观测噪声则取测距码码元长度的百分之一，对于该仿真系统来说，伪距测量误差取0.000 5 m，则 σP=σPSG1=σPSG2=σPGS=0.0005 ，根据误差传播定律，检验量 ΔN1和 ΔN2的中误差分别可以表示为：

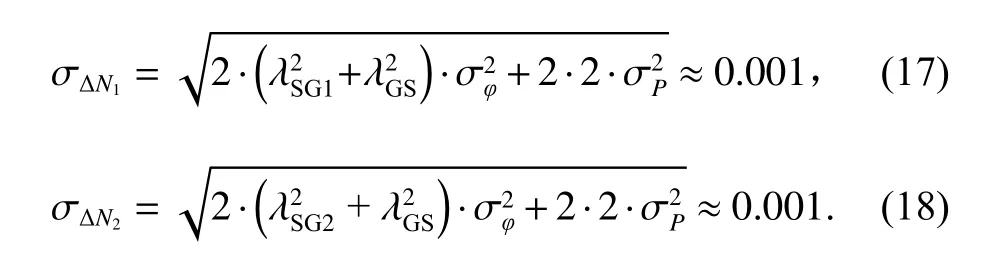
以3倍中误差为检验量阈值，即检验量|ΔN|＞0.003 ，历元t到历元t+1 发生了周跳，反之，则没有发生周跳. 检验量阈值除以对应波长可转换为以周为单位的量，可以得出，三频组合法理论上 ΔN1检验量可以探测出0.311周以上的周跳， ΔN2检验量可以探测出0.215周以上的周跳. 另外，根据式(15)与式(16)可知，当周跳比和频率比相同时无法探测周跳，该方法失效. 针对这种情况，需要另外的组合弥补该方法的不敏感周跳探测，且两个检验量方程三个未知量，无法解算周跳，于是本文选择结合MW组合可互补不敏感周跳的探测，而且可以联立解算周跳.

2.2 MW组合探测周跳

MW组合法[7,13-16]通过宽巷相位减窄巷伪距，消除星地间几何距离、星地间钟差以及大气误差的影响，有效利用了双下行观测数据，并联立三频组合解算周跳. 根据前文伪距相位观测方程，MW组合观测方程可表示为

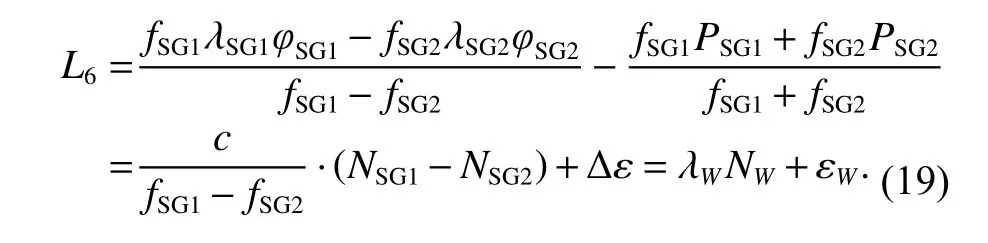
式中：fSG1和fSG2为双下行微波链路频率； λW为宽巷波长；NW为宽巷模糊度； εW为组合观测噪声. 由此可以得到宽巷模糊度为

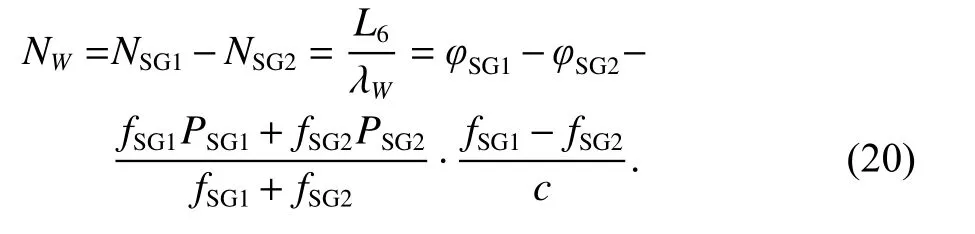
通过组合后的宽巷模糊度已经消除了星地间几何距离、星地钟差以及大气误差等误差因素，在不考虑多路径效应的前提下仅剩余观测噪声的影响，且通过组合后的宽巷波长较长其测量噪声也相应变小.Blewitt通过递推公式推演出第一个历元到第t个历元的宽巷模糊度均值 〈NW〉t和方差，递推公式如下：

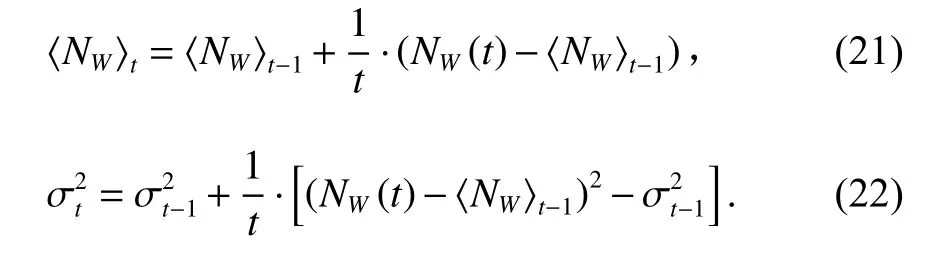
式中：NW(t) 为第t个历元的宽巷模糊度； 〈NW〉t为前t个历元宽巷模糊度的平均值；为前t个 历元 的 方 差.通过历元间宽巷模糊度差分判断是否存在周跳，若满足 |NW(t)-〈NW〉t-1|≥4σt-1以 及 |NW(t+1)-NW(t)|≤1 ，则认为第t个历元发生周跳. 根据上文中相位及伪距的观测误差计算出MW组合的中误差为 σΔNW≈0.0258 ，以3倍中误差为探测阈值，可以得到阈值为±0.077 4，即 | ΔNW|＜0.0774 ，历元t到历元t+1 没有发生周跳，反之，历元间则发生周跳.

MW组合法探测周跳可以弥补三频组合探测周跳中的不敏感周跳，但对于 ΔNSG1/ΔNSG2=1/1 的周跳比，该方法也将失效，而三频组合法可以弥补对应周跳的探测，两种方法相辅相成，可探测出不同类型的周跳.

2.3 周跳的修复

三频组合以及MW组合均存在不敏感周跳对，两种方法互补可以探测出预设的周跳对，并确定组合周跳所在历元，根据联立三组线性无关的检验量方程，对周跳进行解算，得到以下矩阵方程

3 实验仿真及结果分析

3.1 周跳探测与修复

本文通过搭建仿真平台对算法进行实验验证，数据样本是通过模拟得到的低轨卫星与某地面站的星地三频双向的观测数据，采样率为1 s，共有332个观测历元.

为检验本文周跳探测算法的有效性和正确性，对该样本数据在不同历元时刻添加不同类型的载波相位周跳，分别包括了小周跳、连续周跳以及不敏感周跳等几种类型，周跳对应的历元和类型如表1所示.

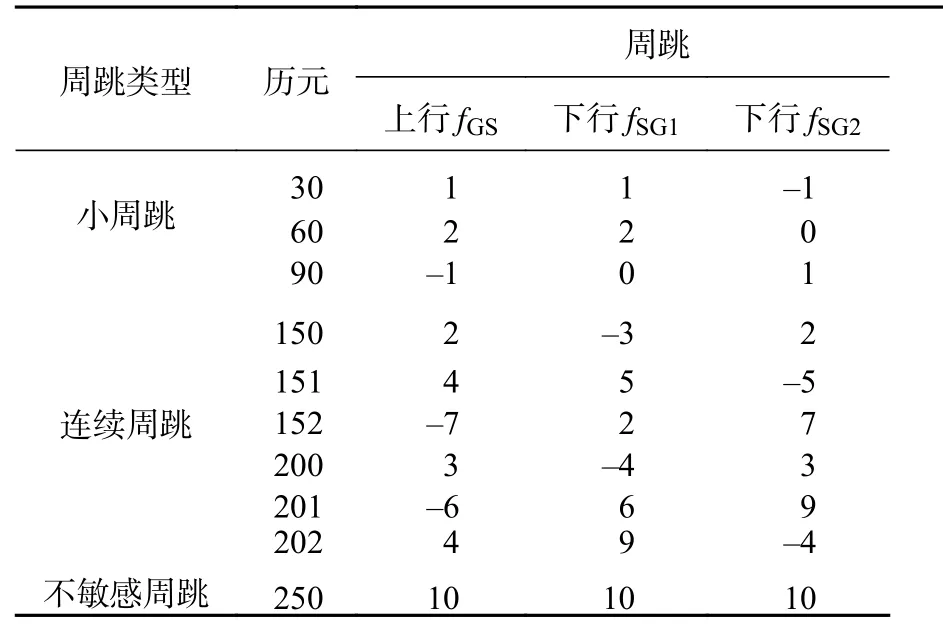
表 1 不同类型周跳

使用本文周跳探测算法对预设周跳的样本数据进行周跳探测，图2～4分别为周跳探测后的各检验量变化情况，可以看出在设置周跳的历元明显检测出超出探测阈值的突变，即在此历元处探测出有周跳存在.

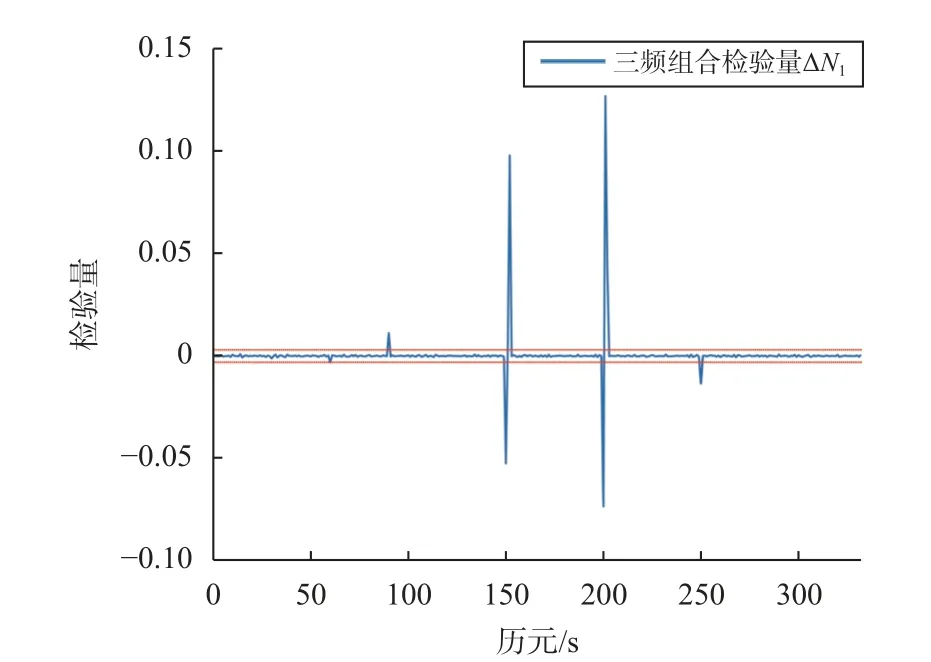
图 2 加入周跳后三频组合 Δ N1 检测序列

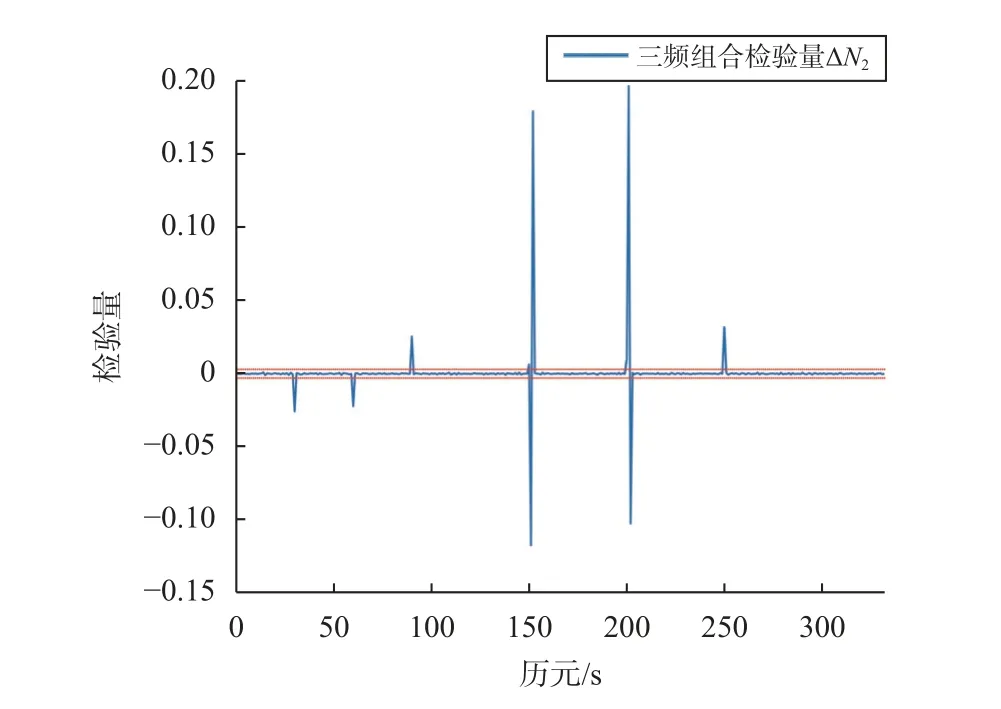
图 3 加入周跳后三频组合 Δ N2 检测序列

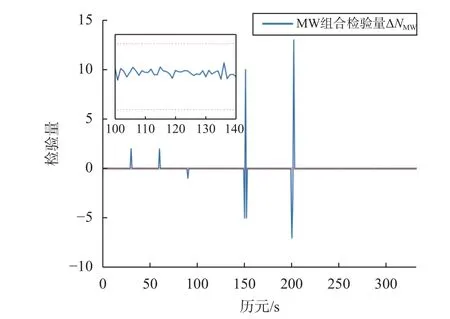
图 4 加入周跳后MW组合检测序列

由图2可知，第30历元上的周跳对(1,1, -1)和第60历元上的周跳对(2,2,0)没有超过探测阈值，经过分析发现由于对应频点的波长较小，且上行fGS和下行fSG1频率接近，当同时发生±1周和±2周周跳时，对应检验量分别为 ± 0.001326+∇Δε 和±0.002652+∇Δε，此时由于检验量变化过小而无法探测出同比例周跳，而发生其他不等比小周跳时，如(1,0)、(2,1)等，均可以探测出来，当周跳值大于等于3时，此类现象不再发生可悉数探测出来，这种现象只出现在检验量ΔN1中 ，从图3看出检验量 ΔN2不存在这种情况，而且ΔN2可以弥补 ΔN1探测出该历元存在周跳，所以综合图2和图3三频组合法可以将所有预设周跳探测出来. 由图4可知，历元30、60、90、150、151、152、200、201、202均探测出有周跳存在，而历元250的周跳对(10,10,10)无法通过MW组合探测出来，这验证了上文所述的MW组合法存在不敏感周跳组合.而利用三频组合法仍可以有效探测，两种组合方法相辅相成，极大地提高了周跳探测的成功率.

所有预设周跳通过两种组合法均可探测出来，通过最小二乘解算矩阵X获得周跳的浮点解，并在相应历元进行修复，不同类型周跳探测与修复结果如表2所示.

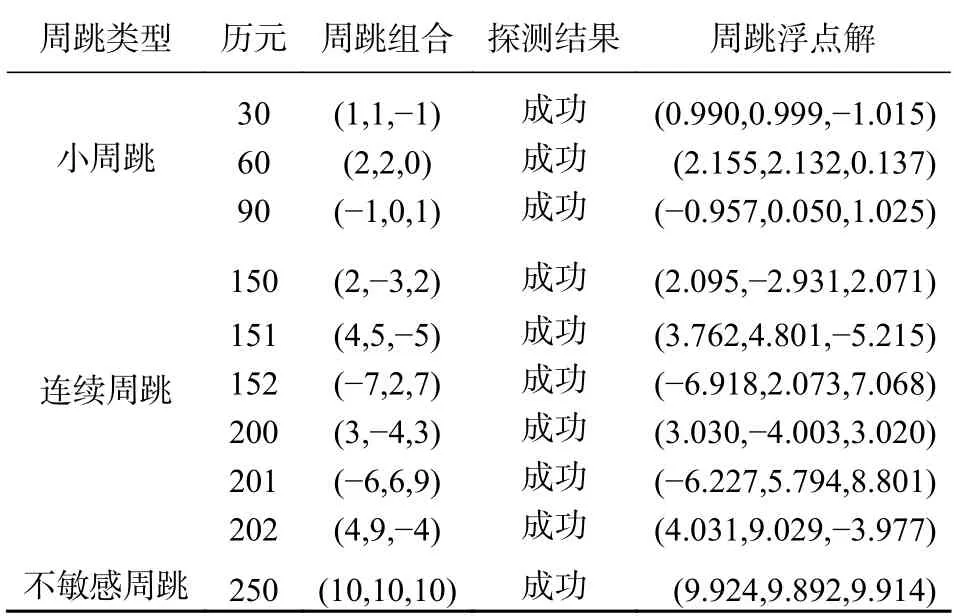
表 2 周跳探测与修复结果

由表2可知，无论是单一历元上的小周跳，还是连续历元出现连续周跳，亦或是在不同频率观测量中出现的不敏感周跳对，本文的方法均可以准确有效地探测出周跳的发生，并确定周跳所在历元，通过最小二乘法解算出周跳浮点解，成功修复相位数据，验证了三频组合法和MW组合法对周跳探测与修复的有效性和正确性.

为了进一步验证本文算法对周跳探测与修复准确性，将周跳探测并修复后的载波相位值与理论的载波相位值作差，以此观察载波相位探测修复的精度.图5～7分别为单上行双下行对应相位伪距修复精度.

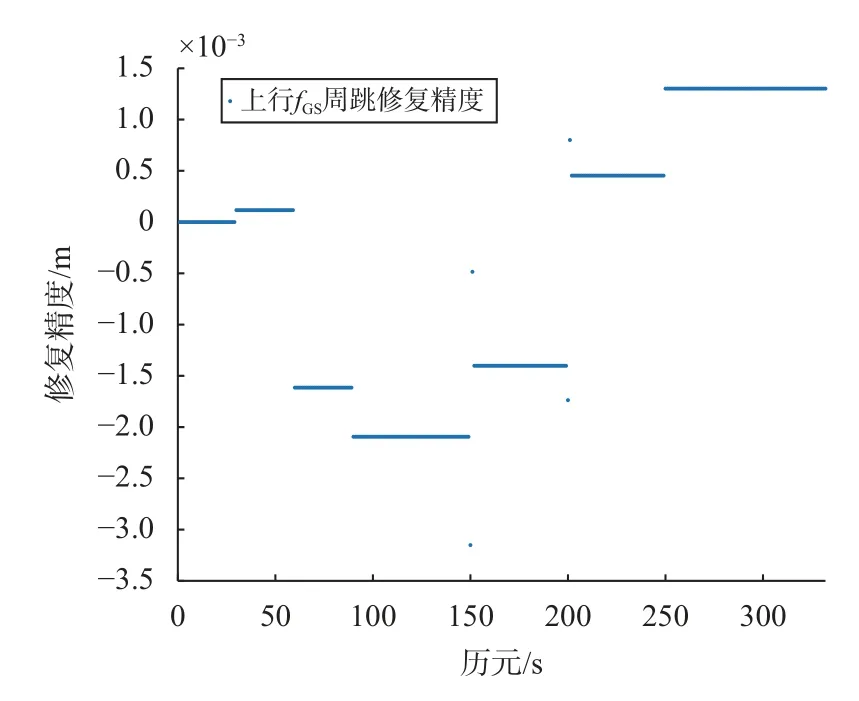
图 5 上 行 fGS 周跳修 复精度

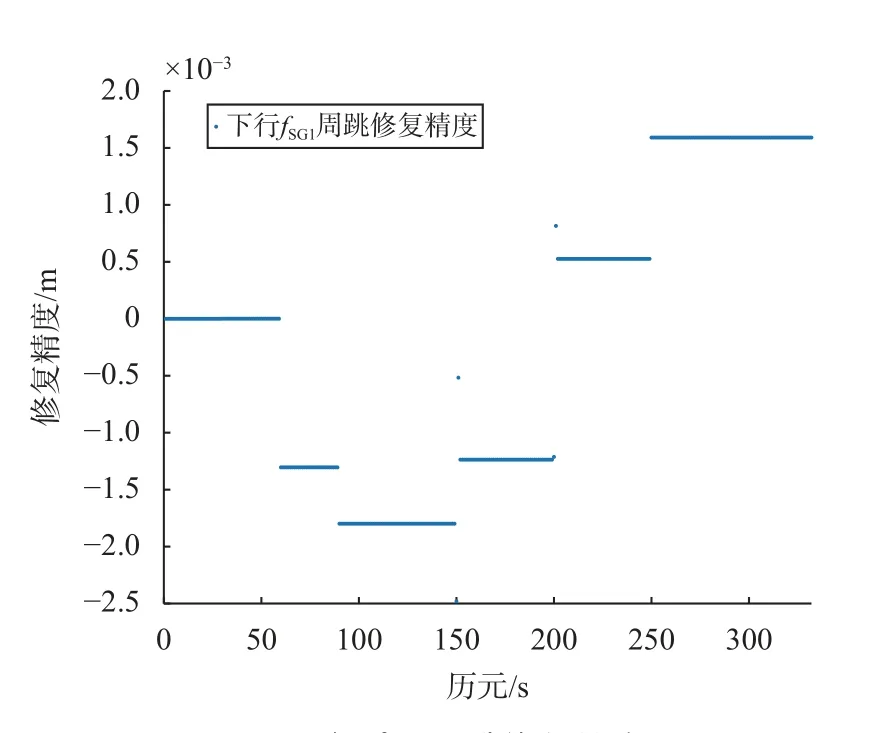
图 6 下行 fSG1 周跳修复精度

图5～7的仿真结果表明，上行链路fGS和双下行fSG1、fSG2周跳修复精度RMS值分别为1.345 mm、1.288 mm和1.737 mm. 由于周跳会对当前历元及之后的历元产生影响，如果在周跳发生历元后再次发生周跳，先前发生的周跳会对之后发生的周跳产生叠加效应，以浮点解修复后的残差依然会产生叠加效应，但从图中可以看出，即使存在叠加影响，各链路周跳修复精度均能达到毫米量级.

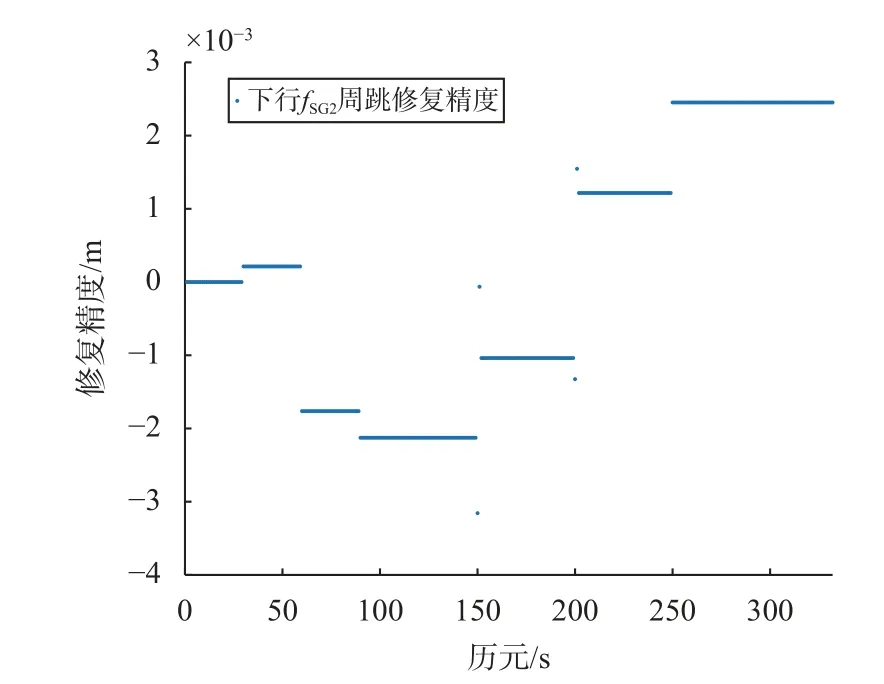
图 7 下行 fSG2 周跳修复精度

3.2 星地双向时间同步性能分析

星地双向时差测量的最终目的是实现高精度的星地时间同步，通过周跳探测修复并将双向测量时间信息归算至同一时刻，并通过模型和算法消除链路中电离层时延、对流层时延、周期性相对论时延和引力时延，最后解算得到星地相对钟差，进一步对星地钟差求其拟合残差的RMS值，分析星地时间同步精度.

按照表1周跳设置方案加入周跳，图8展示了包含周跳的原始数据只进行空间距离归算的星地双向时间同步性能.

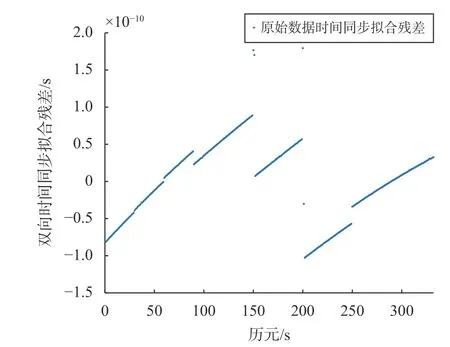
图 8 原始数据双向时间同步性能分析

为了区别周跳探测与修复前后双向时间同步的性能改进，图9展示了未进行周跳探测与修复，只进行链路时延数据处理的双向时间同步性能.

通过周跳探测与修复以及链路时延数据处理，图10展示了周跳修复后且进行时延处理后的星地高精度双向时间同步性能.

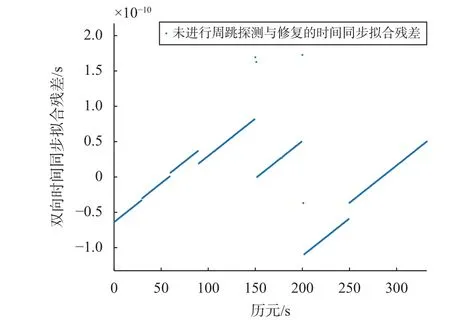
图 9 未探测修复双向时间同步性能分析

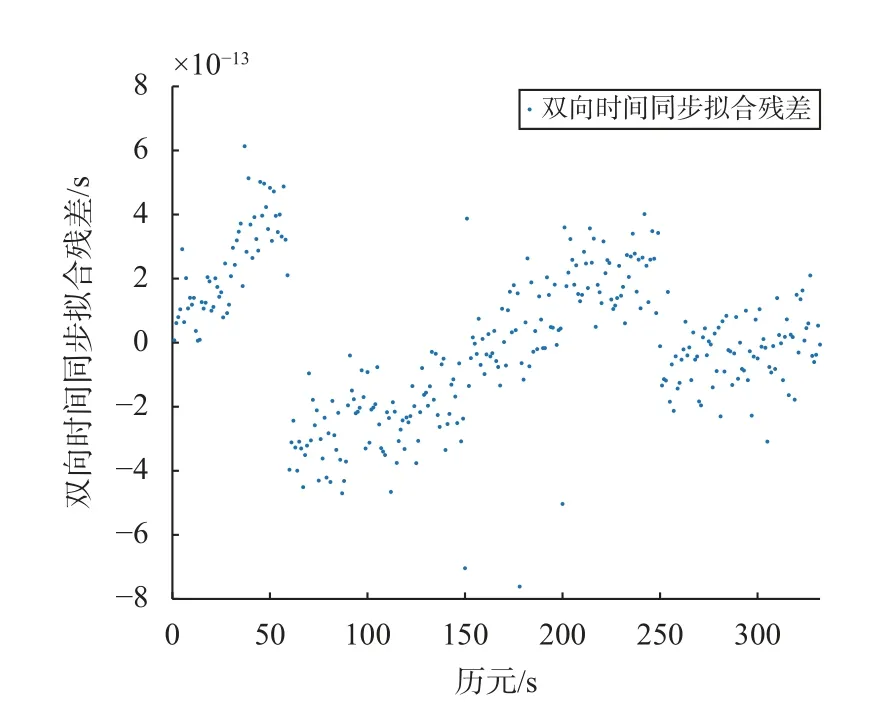
图 10 数据处理后双向时间同步性能分析

由图10可知，其双向时间同步拟合残差整体在-0.8×10-12s至0.8×10-12s间波动，波动趋于稳定，整个弧段中由于周跳修复残差的影响，在周跳发生历元出现了不同程度的跳变，但始终保持在指标范围内. 综合图8～10双向时间同步性能，经计算包含周跳的原始数据双向时间同步精度RMS为50.83×10-12s，而未进行周跳探测与修复只进行链路时延数据处理的双向时间同步精度RMS为49.18×10-12s，经过周跳修复和链路时延数据处理后的双向时间同步精度RMS可达0.225 6×10-12s，相较于未探测修复的时间同步结果提高了2个数量级. 因此，本文的周跳探测与修复方法对星地双向时间同步性能实现了明显提升.

4 结束语

为实现高精度星地时间比对，将载波相位测量融入双向时差测量中，本文提出一种适用于三频组合模式的双向周跳探测与修复方法，并联合MW组合法实现不同类型周跳的探测与修复. 两种方法相互弥补周跳探测从而实现所有预设周跳的有效探测，上下行三条微波链路均可探测出周跳的存在并实现毫米级周跳修复精度. 进一步对基于载波相位测量的星地双向时差测量系统的星地时间同步性能进行分析，在经过周跳探测与修复，以及链路时延数据处理，其星地时间同步精度优于0.3×10-12s.