汽车尾气温差发电系统车载兼容性多目标优化研究

全 睿 李 涛 乐有生 常雨芳 谭保华

1.湖北工业大学太阳能高效利用及储能运行控制湖北省重点实验室，武汉，4300682.湖北工业大学太阳能高效利用湖北省协同创新中心，武汉，4300683.湖北工业大学理学院，武汉，430068

0 引言

随着社会的发展，汽车的保有量急剧增加，依旧占据汽车发动机主流的内燃机效率普遍较低，大约30%～40%的燃油能量以尾气的形式直接排入大气[1]，造成了极大的能源浪费与环境污染。温差发电技术作为最有前途的绿色环保技术之一，可以利用热电材料和器件将热能直接转换为电能。温差发电技术具有模块小、无运动部件、寿命长等一系列优点[2-3]，可以有效回收汽车尾气废热进行发电并用于车载系统，从而提高传统燃油发动机的燃料利用率，降低其排放污染[4-5]。然而，汽车尾气温差发电系统在整车集成时除了谋求其最大发电功率，还需要考虑其车载兼容性问题。

热交换器作为汽车温差发电系统的重要部件，其流场结构和尺寸参数直接影响着系统的发电功率以及发动机的排气背压，而排气背压的增加会导致发动机燃烧不充分，其动力性、燃油经济性和排放性能可能会恶化，这种此消彼长的现象很有可能抵消甚至超过温差发电所带来的节能效益。因此，在尽可能降低对发动机原有性能影响的基础上，优化热交换器结构参数，增大温差发电系统的发电功率，提高汽车尾气温差发电系统的车载兼容性是十分必要的。WANG等[6]利用多岛遗传算法对平板式热交换器内部翅片的结构参数进行了优化，在提高其温度分布均匀性的同时降低了其压力损失。HE等[7]利用Fortron程序进行数值模拟，研究了热交换器的尺寸、传热、流动阻力特性以及对温差发电性能的影响，并在合理压降下确定其最高净输出功率时热交换器最佳横截面积为0.0056 m2，最佳高度为5 mm，最佳长度为0.56 m。何嘉华等[8]综合利用神经网络和遗传算法，以热交换器的排气背压和质量为约束条件对平板式热交换器的热通道结构参数进行了优化设计，在排气背压和质量可控的情况下提高了热电器件的两端温差。上述平板型热交换器虽然便于安放热电器件，但热源利用率低，尾气流动背压相对较高，而圆筒式热交换器的表面利用率高，表面温度分布较平板式更为均匀，背压也比平板式更低。舒歌群等[9]利用GT-Power排气背压模型对一款适用于柴油发动机的圆筒式温差发电装置提出了加装不同尺寸导流装置的优化方案，当采用60 mm的导流装置时，在背压合理的情况下取得最大系统净输出功率为651.1 W，比原系统提高了49.2%。刘越等[10]基于CFD模型对不同肋片数目、肋片高度、肋片前后端高度和装置端口长度等进行仿真计算，以热端表面平均温度和流场均匀性为评价指标，确定了优化方案，相比原始方案其冷热端平均温差提高了8.8%, 系统输出功率提高了5.8%。上述研究均是追求温差发电系统发电功率最大化的优化设计，未考虑排气背压对其发电功率和发动机性能的影响(或假定热交换器的压力损失对发动机影响忽略不计)，实际情况是增大的背压会急剧恶化发动机的原有动力性、燃油经济性和排放性能。因此，上述设计的汽车尾气温差发电系统尽管发电量可观，但其车载兼容性不高，制约了汽车尾气温差发电系统的节能与减排功效。

本文考虑到圆筒式热交换器的背压较低且其表面温度分布较平板式更为均匀，针对汽车尾气温差发电系统用六边形结构热交换器搭建CFD模型，研究三种热交换器翅片结构在不同入口流速和温度下对热交换器进出口压力损失以及换热温度的影响，采用多目标灰狼算法对热交换器内部翅片的长度、宽度、角度及分布间距进行优化设计，以提高热交换器表面温度和汽车尾气温差发电系统的发电功率，同时降低发动机的进出口压力损失。

1 汽车温差发电系统结构

本文设计的汽车尾气温差发电系统其结构如图1所示，热电器件夹紧在热交换器和冷却水箱之间，热交换器接入排气管吸收尾气余热为热电器件提供热端温度，冷却水箱为热电器件冷端散热，从而实现温差发电，热电器件产生的直流电能经过DC/DC变换后给车载电器供电[11]。其中，六边形热交换器采用黄铜制造，其具体尺寸如图2所示[12]。全长为440 mm，壁厚为2 mm，外径为53 mm，中间换热段的总长为260 mm。

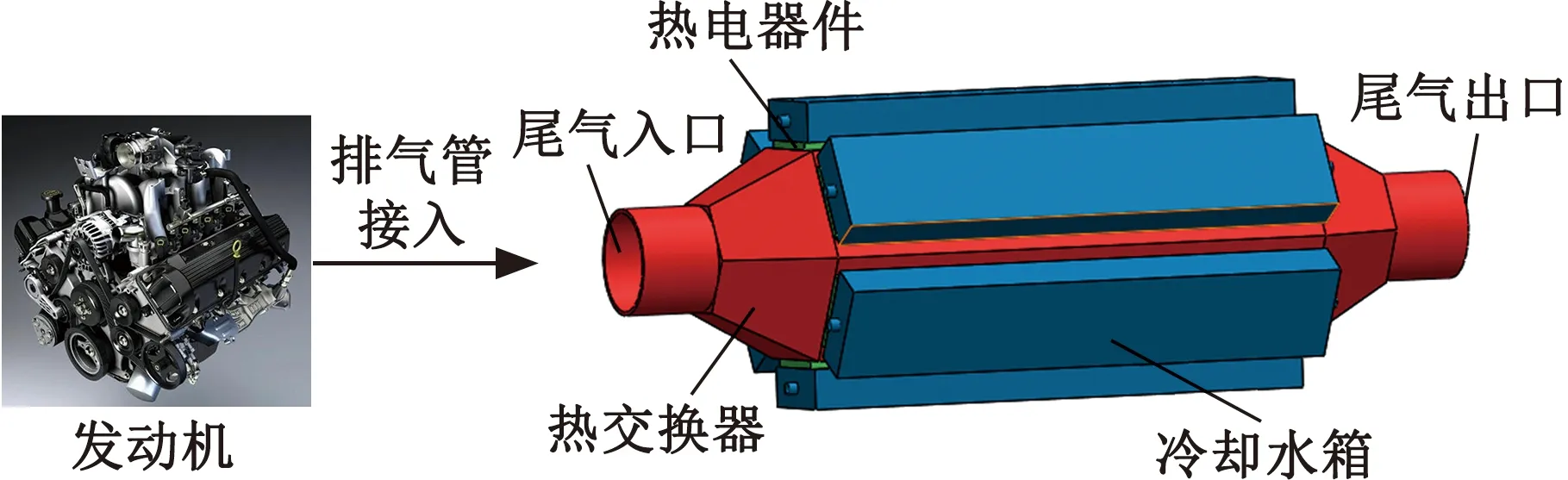
图1 汽车尾气温差发电系统结构示意图Fig.1 The structure of the automobile exhaust thermoelectric generator system

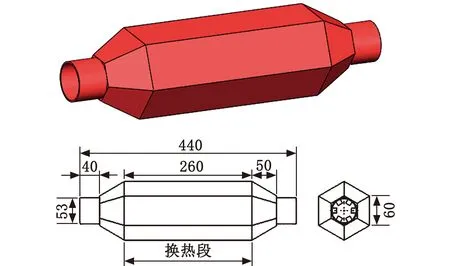
图2 六边形热交换器尺寸图Fig.2 Hexagonal heat exchanger size

2 热交换器数值模拟与仿真分析

2.1 设计变量的选取

为了提高热交换器的吸热和储热能力，其内部安置了大量翅片以加强热交换器内表面与尾气之间的对流。针对图2所示的热交换器，保持其外部长度尺寸不变，选取翅片的长度、角度、宽度以及分布间距作为设计变量对其进行车载兼容性优化。图3是热交换器的1/2截面图，翅片厚度固定为2 mm，首列翅片与换热段始端的距离始终为20 mm，翅片皆居中放置。变量A是翅片与换热端内表面之间的角度，翅片的一端面向热交换器的入口；变量W是翅片的宽度；变量L是翅片的长度；变量S是翅片间的间距，翅片默认填满整个换热段。

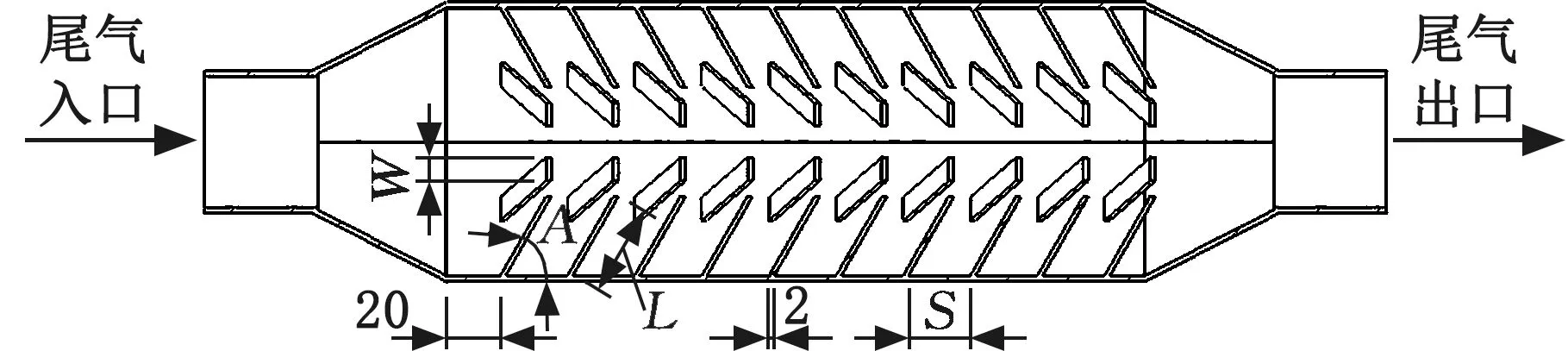
图3 热交换器的截面图Fig.3 A cross-section of the heat exchanger

2.2 热交换器数值模拟

根据流体动力学基本理论，汽车尾气在流动过程中始终遵循质量守恒定律、动量守恒定律和能量守恒定律。为了减少不必要的计算量，假设尾气具有常物性且不可压缩，为稳态流动状态，在热交换器入口处流速均匀。采用的三大方程具体形式如下。

质量守恒方程：

(1)

动量守恒方程：

(2)

(3)

(4)

能量守恒方程：

(5)

式中，ux、uy、uz分别为流速在x、y、z方向上的速度分量；ρ为流体密度；μ为动力黏度；cp为流体质量定压热容；T为温度；k为热导率。

在SolidWorks中建立上述六边形热交换器模型并导入DesignModeler中填充流体。考虑到计算量以及模型的对称性，将其对称为原模型的1/4，采用四面体划分网格，网格单元质量最低为0.17。将划分好的网格导入FLUENT中设置边界条件，仿真类型为稳态并开启能量方程，选择可实现的k-ε模型，壁面函数选择增强型壁面函数。由于固体外表面和空气的对流传热系数一般为5～25 W/(m2·K)，仿真时设置热交换器外表面与空气的对流传热系数为20 W/(m2·K)，外部环境温度采用默认的300 K，热交换器入口设置流速为20～40 m/s，温度为400～600 K，设置出口相对压力为0。流体域和固体域相临的网格面设置为耦合面。考虑到收敛的速度，压力速度耦合算法采用Coupled算法，压力、动量、湍流动能、湍流耗散率和能量皆设置为Second Order Upwind，采用面积加权平均法计算换热段表面的平均温度和热交换器入口与出口之间的压力损失。

2.3 仿真结果及边界条件的确定

根据图2所示的热交换器外部尺寸，选取三组不同翅片结构的热交换器研究不同入口流速和入口温度对换热温度的影响以及不同流速对进出口压力损失的影响，其中，结构1：L=40 mm，W=6 mm，A=60°，S=20 mm；结构2：L=37 mm，W=8 mm，A=80°，S=30 mm；结构3：L=42 mm，W=7 mm，A=70°，S=25 mm。

图4所示为入口最高温度为600 K时不同入口尾气流速下热交换器的进出口压力损失。可见，入口流速与热交换器的进出口压力损失成正比，尾气流速较低时，不同翅片结构热交换器的压力损失差距很小，而随着尾气流速的增加，不同翅片结构热交换器的压力损失差距愈发明显。入口最高温度为600 K时不同入口尾气流速下热交换器换热段的温度如图5所示。入口流速的增加会提高热交换器的换热段的温度，但提升幅度会随着流速增加而越来越小。图6所示为入口最大流速为40 m/s时不同入口温度下热交换器换热段的温度，可见入口温度与换热段表面温度近似成线性正比，换热能力越高的结构曲线斜率越高，随着入口温度的增加，不同结构热交换器换热段的储热吸热性能差距也愈发明显。

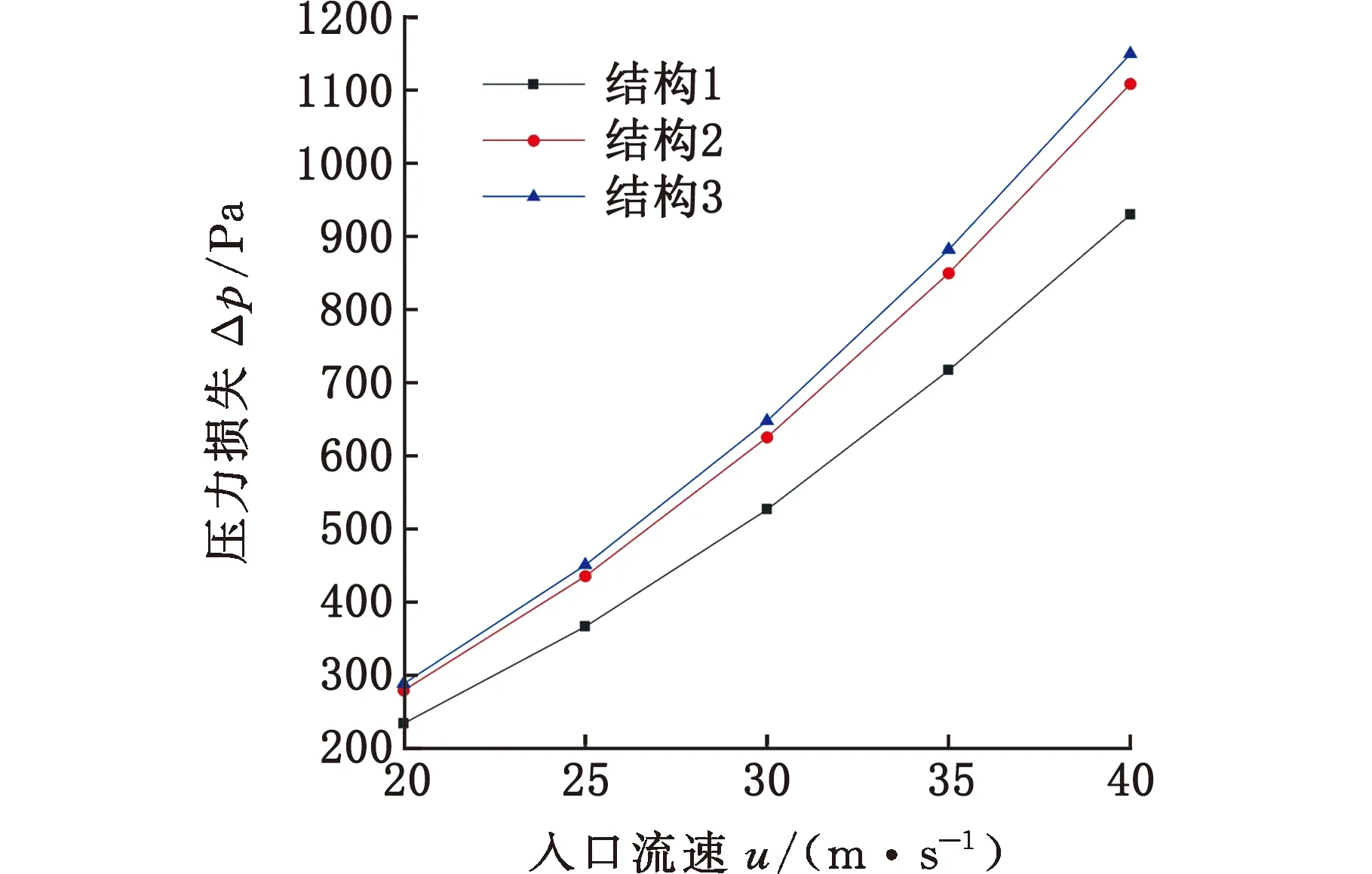
图4 不同入口流速下进出口压力损失Fig.4 Pressure loss between inlet and outlet with different inlet flow speeds

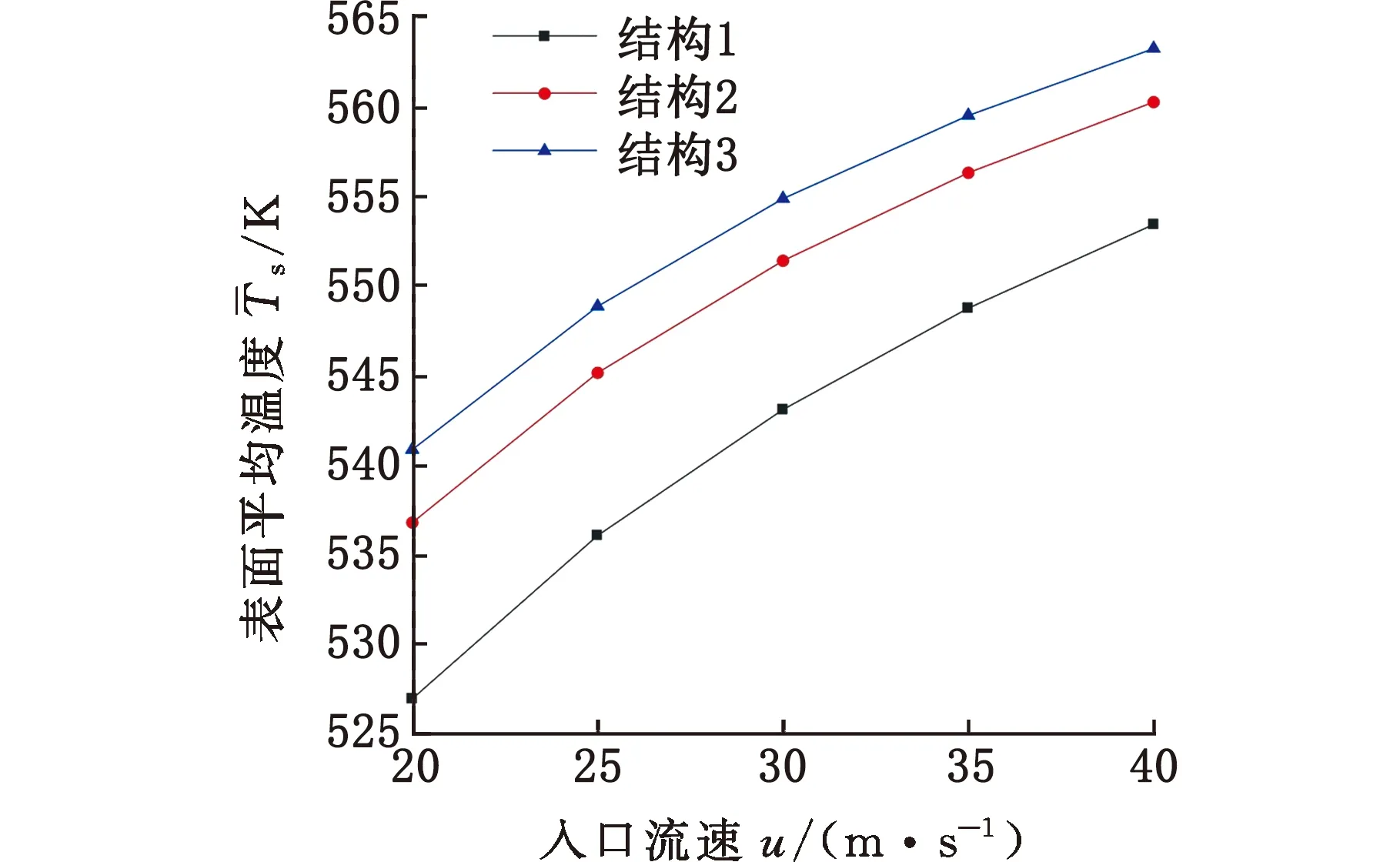
图5 不同入口流速下热交换器换热段表面平均温度Fig.5 Average surface temperature of heat exchanger with different inlet flow speeds

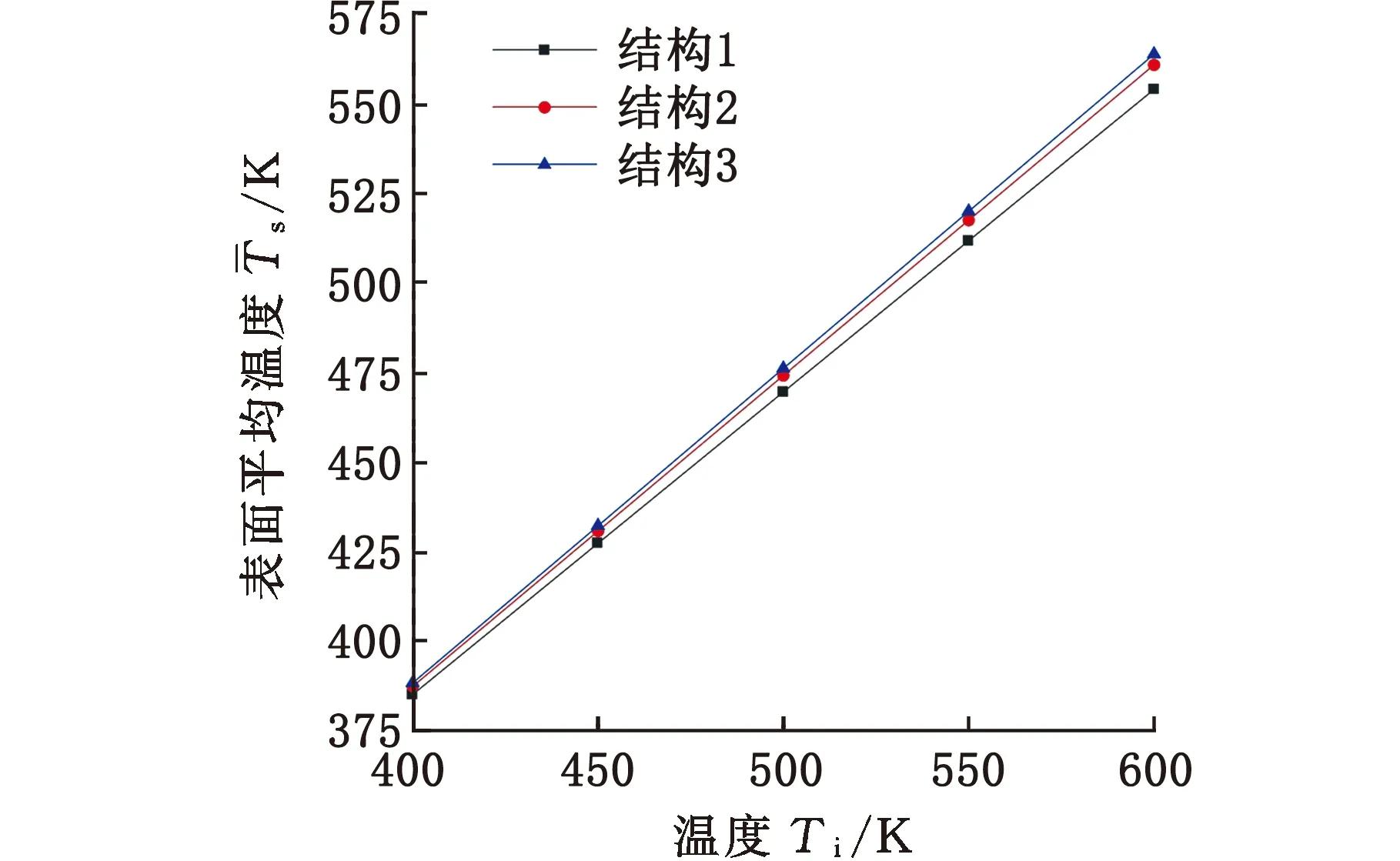
图6 不同入口温度下热交换器换热段表面平均温度Fig.6 Average surface temperature of the heat exchanger with different inlet temperatures

考虑到入口流速为40 m/s、入口温度为600 K时，不同结构的热交换器其换热温度与压力损失差距最为明显，为了方便优化设计，具体边界参数设置见表1。

表1 热交换器边界条件参数

3 高斯代理模型

3.1 正交法设计试验

正交设计法是研究多因素多水平系统的主要试验设计方法之一，在不影响最终试验结果的基础上，根据正交性从试验中挑选代表性强的部分点进行试验，在极大减少工作量的同时，使得试验结果尽量符合实际情况。

图7a～图7c分别为结构1、2和3在入口流速为40 m/s时的速度云图，可见，结构1、2、3的翅片对气体流动有着明显的阻挡作用，热交换器中心区域的流速要远高于翅片间隔之间的流速，尾气大多都是从中心区域通过，这使热交换器对尾气的压力损失较小。同时可以看到若翅片的角度和长度过小，将导致翅片对气体流动几乎不起扰动作用。

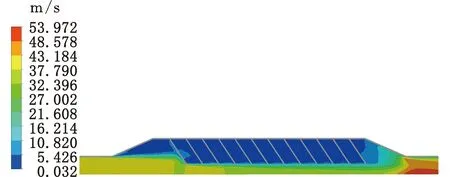
(a)结构1

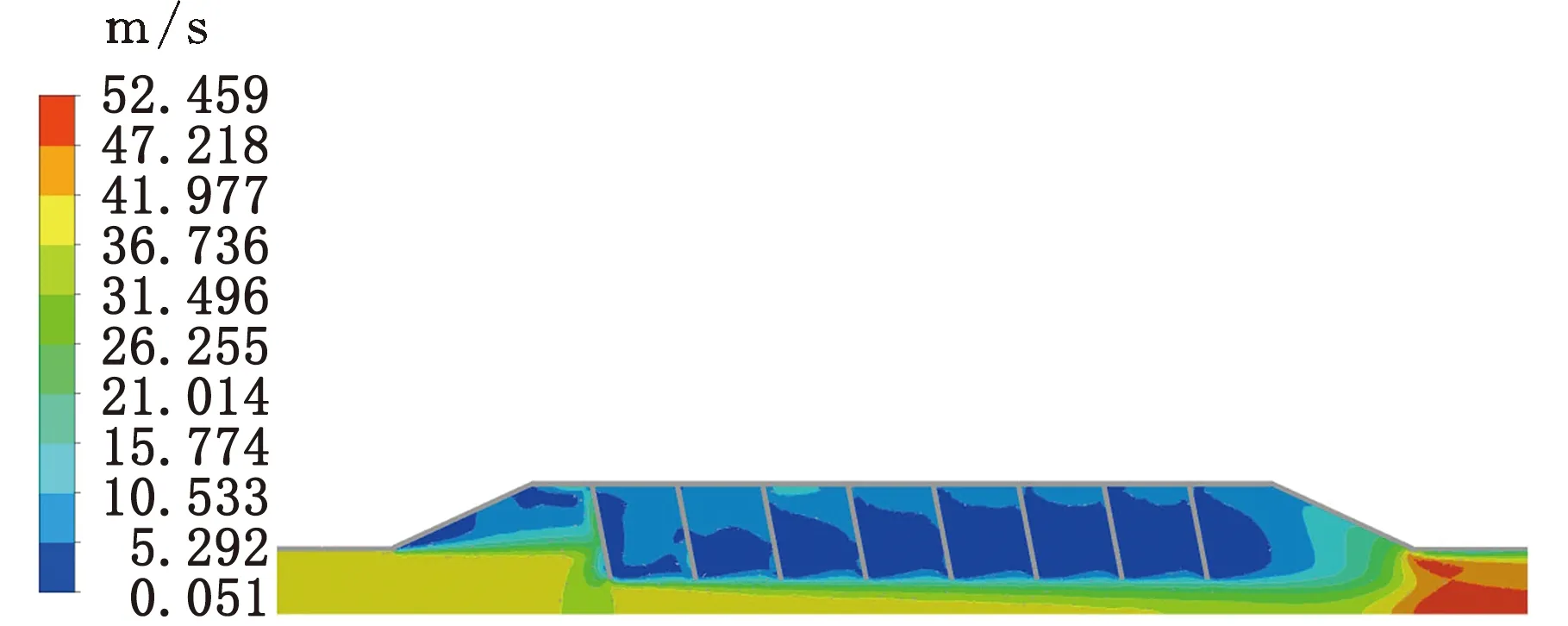
(b)结构2

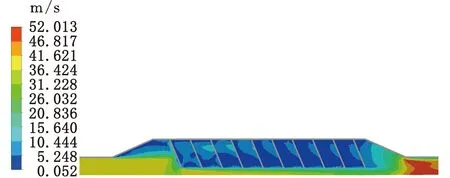
(c)结构3图7 入口流速为40 m/s时三种结构的速度云图Fig.7 Velocity cloud map of three kinds of structure when the inlet speed is 40 m/s

考虑到优化的精确度，选择四因素四水平的正交表L(16)进行试验，见表2。根据表1设置的边界条件分别对16组结构参数进行数值模拟。

3.2 高斯过程拟合

当设计变量和优化目标之间的关系很难用精确数学表达式表示时，需要拟合试验点数据，建立设计变量和响应值的关系。由于上述正交设计所

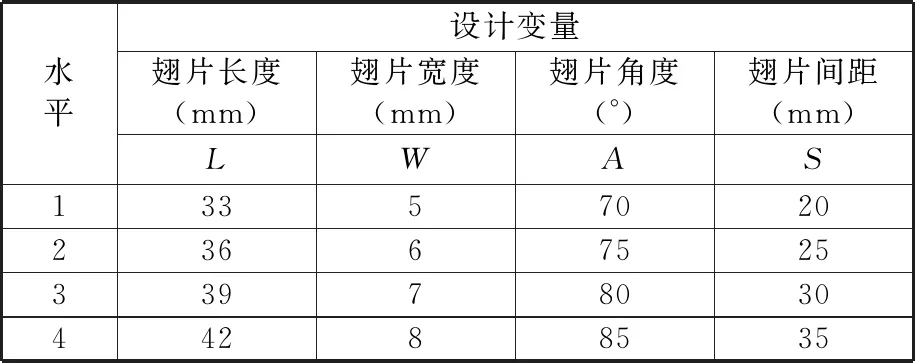
表2 因素水平表

得的样本空间中只有16个试验点，为了保证拟合的精确度，采用高斯过程回归算法建立代理模型，对输入和输出的关系进行拟合，确定目标输出的条件分布。高斯过程对处理高维度、非线性、低样本的问题有很好的适应性。利用MATLAB的fitrgp函数分别对进出口压力损失和换热段表面平均温度建立回归模型。压力损失回归模型的协方差函数选择Matern52，温度回归模型的协方差函数选择Matern32，拟合方式和预测方式均选择高斯过程回归。

决定系数R2又称为拟合优度，可以用来评判回归模型的拟合精度，其取值范围为0～1，越靠近1，说明回归模型的拟合精度越高，默认情况下若R2>0.9，则就可以表示回归模型的拟合较为精确。决定系数的数学表达式为

(6)

Sres=∑(y-f)2

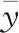
经过计算，压力损失的决定系数为97.21%，表面平均温度的决定系数为97.95%，两者皆大于90%，表明高斯过程回归的拟合精度较高。高斯过程回归模型拟合精度散点图见图8，纵横坐标分别对应16个试验点的仿真值和预测值，散点大多靠近y=x的对角线上，说明仿真值与预测值近乎相等。从设计空间中选取不同于16个正交试验点的另外三组翅片结构参数(依次命名为结构4、5、6)，分别进行回归模型预测与数值模拟，验证回归模型的可信度，对比结果见表3。可见，结构4、5、6三组样本的仿真值与预测值的相对误差均小于3%，可认为高斯过程回归的拟合精度较高，可信度高，能满足多目标寻优的精度要求。

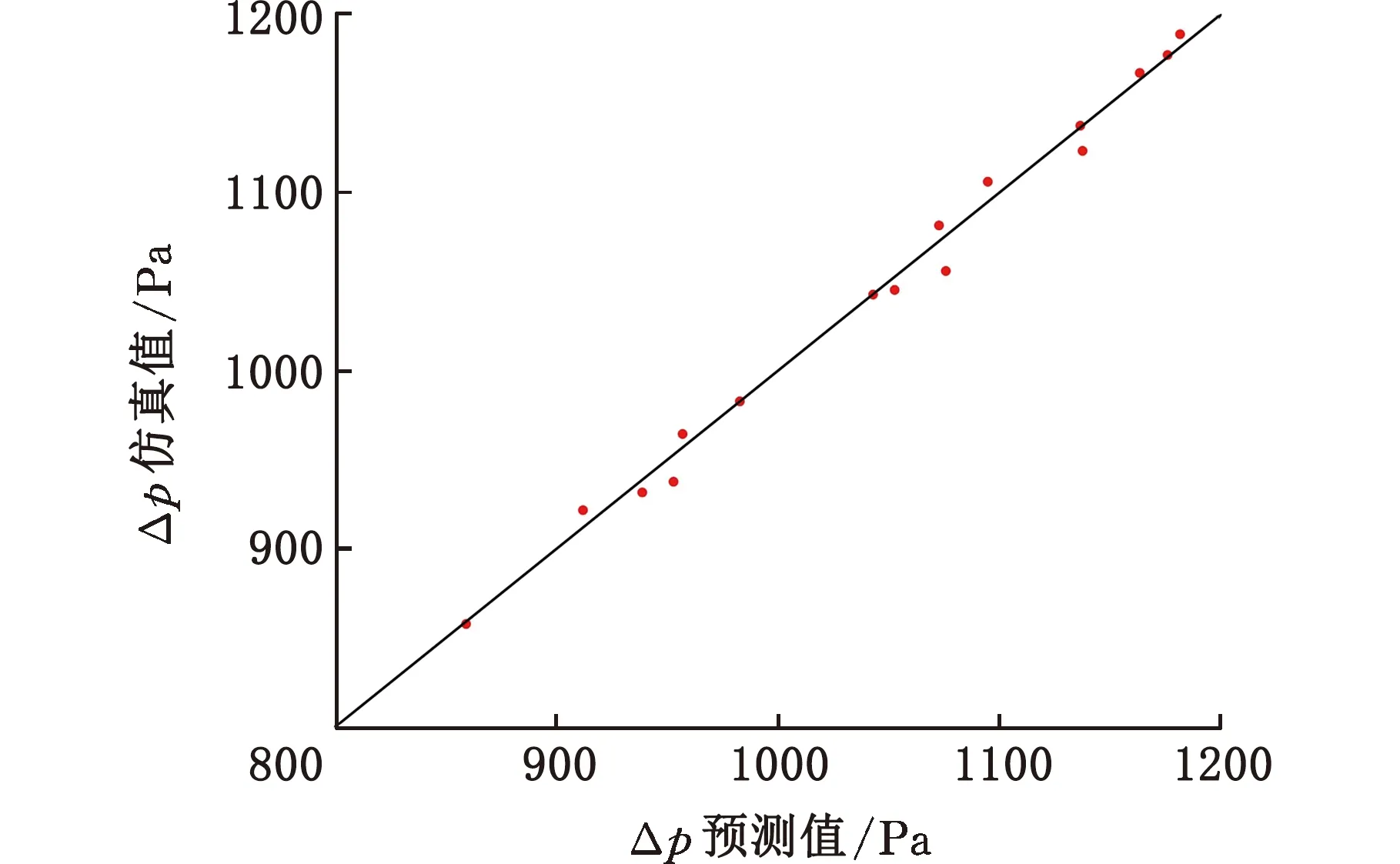
(a)压力损失代理模型

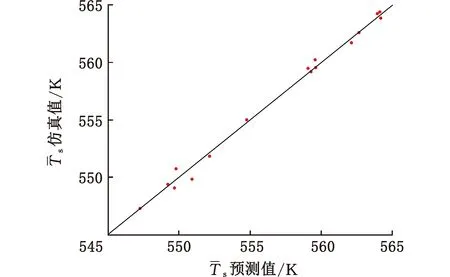
(b)表面平均温度代理模型图8 高斯过程回归模型拟合精度散点图Fig.8 Gauss process regression model fitting precision scatterplot

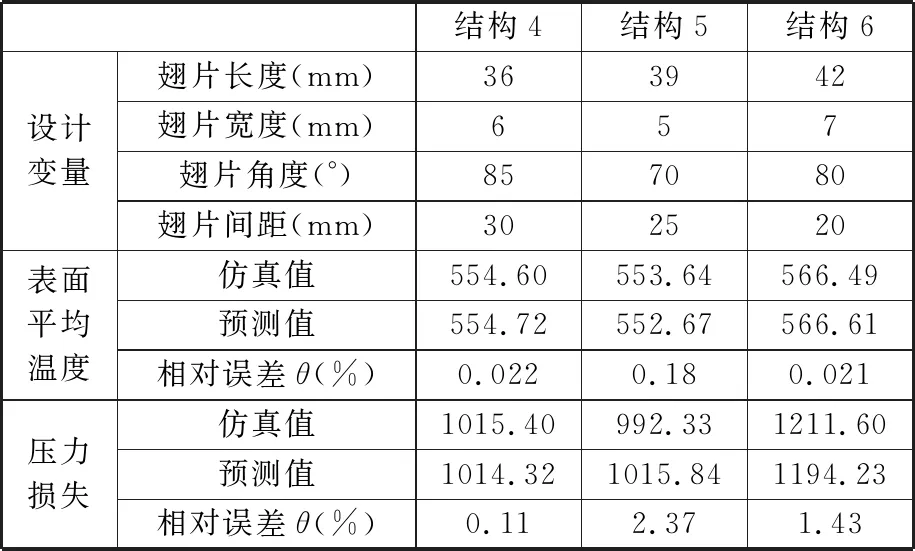
表3 仿真值与模型预测值比较

4 车载兼容性多目标优化

4.1 热交换器车载兼容性优化模型的构建

在热交换器车载兼容性优化问题中，需要考虑热交换器换热段表面平均温度和进出口压力损失之间的相互耦合关系，即换热段表面温度最高的同时进出口压力损失最低是其车载兼容性的优化目标，具体优化模型如下：

maxT(L，W，A，S)

(10)

min Δp(L，W，A，S)

(11)

s.t.L∈X1，W∈X2，A∈X3，S∈X4

(12)

式中，T为热交换器换热段表面平均温度函数；Δp为进出口压力损失函数；X1、X2、X3、X4分别为设计变量翅片长度L、翅片宽度W、翅片角度A、翅片间间距S的设计空间，X1、X2、X3、X4的范围分别设为[33，42]、[5，8]、[70，85]、[20，35]，其中，翅片长度L、翅片宽度W和翅片间间距S的单位为mm，翅片角度A的单位为°。

4.2 基于灰狼算法的多目标优化实现

灰狼算法(grey wolf optimizer,GWO)是一种新型的群体智能优化算法，具有收敛快、调参少和实现简单的优点，它主要分为社会等级制度、包围猎物、搜寻猎物以及攻击猎物四部分，以迭代的方式不断接近直至找到猎物(最优解)。灰狼的社会等级分为四层[13]，α狼又称头狼，负责狼群的管理以及各种事宜的决策；β狼辅助头狼进行决策与安排，是头狼的候选人；δ狼听从前两等级的指示，负责侦察、看护等，年老的α狼与β狼也会降为δ狼；ω狼是社会的最底层，听从其他等级的指挥，主要负责平衡种群内部关系。在捕食过程中，α狼、β狼与δ狼分别对应着当前行动的最优解、优解与次优解，狼群会根据距离猎物位置的优劣程度重新选出α狼、β狼与δ狼，ω狼始终向着α狼、β狼与δ狼的位置移动。

多目标灰狼优化算法(multi-target grey wolf optimizer,MOGWO)需要在传统灰狼算法的基础上引用多目标处理机制[14-15]：一是引入外部种群archive存放每次迭代中的最优个体，并根据支配关系不断更新种群内部个体。如果新个体被archive中的个体所支配，则不加入archive中；如果新个体支配archive中一个或多个个体，则加入archive中替换掉被其支配的个体；如果新个体与archive中个体互不支配，则不加入archive中。但archive的上限是固定的，为防止超出archive种群上限以及维持种群的多样性，计算archive内所有个体的目标函数值，并以极值为上下限平均划分区间，每个区间内所有值的集合即为个体目标函数所在组，若在迭代过程中，archive内部空间已满，则在最拥挤的组中随机剔除某些个体，并将新加入的个体插入不拥挤的组中。二是优化头狼选择机制。archive空间内存有迭代过程中产生的所有非支配最优解，采用轮盘赌的方式从中选取头狼(此处α狼、β狼与δ狼皆称为头狼)。

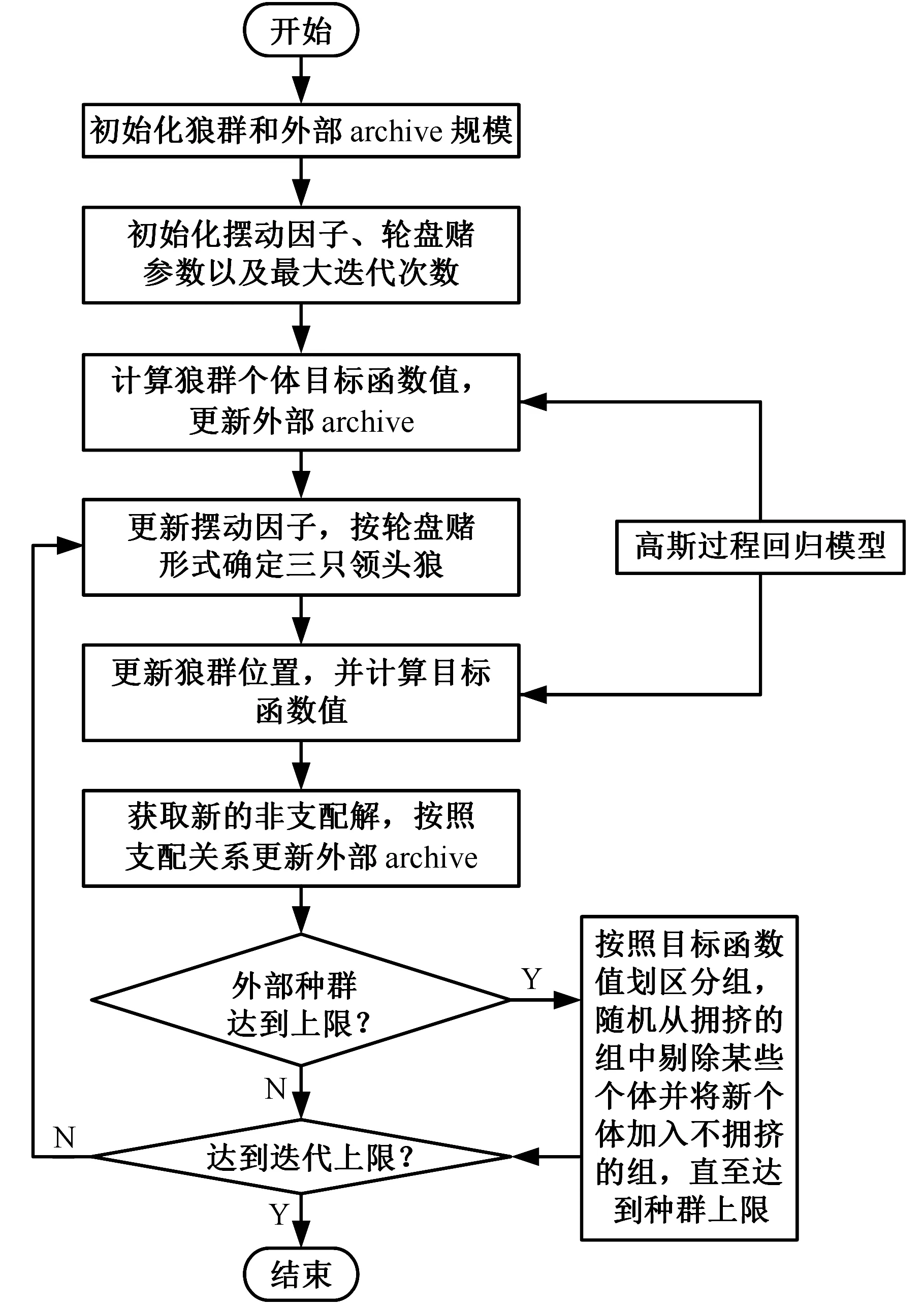
图9 多目标灰狼算法流程图Fig.9 Multi-target grey wolf algorithm flowchart

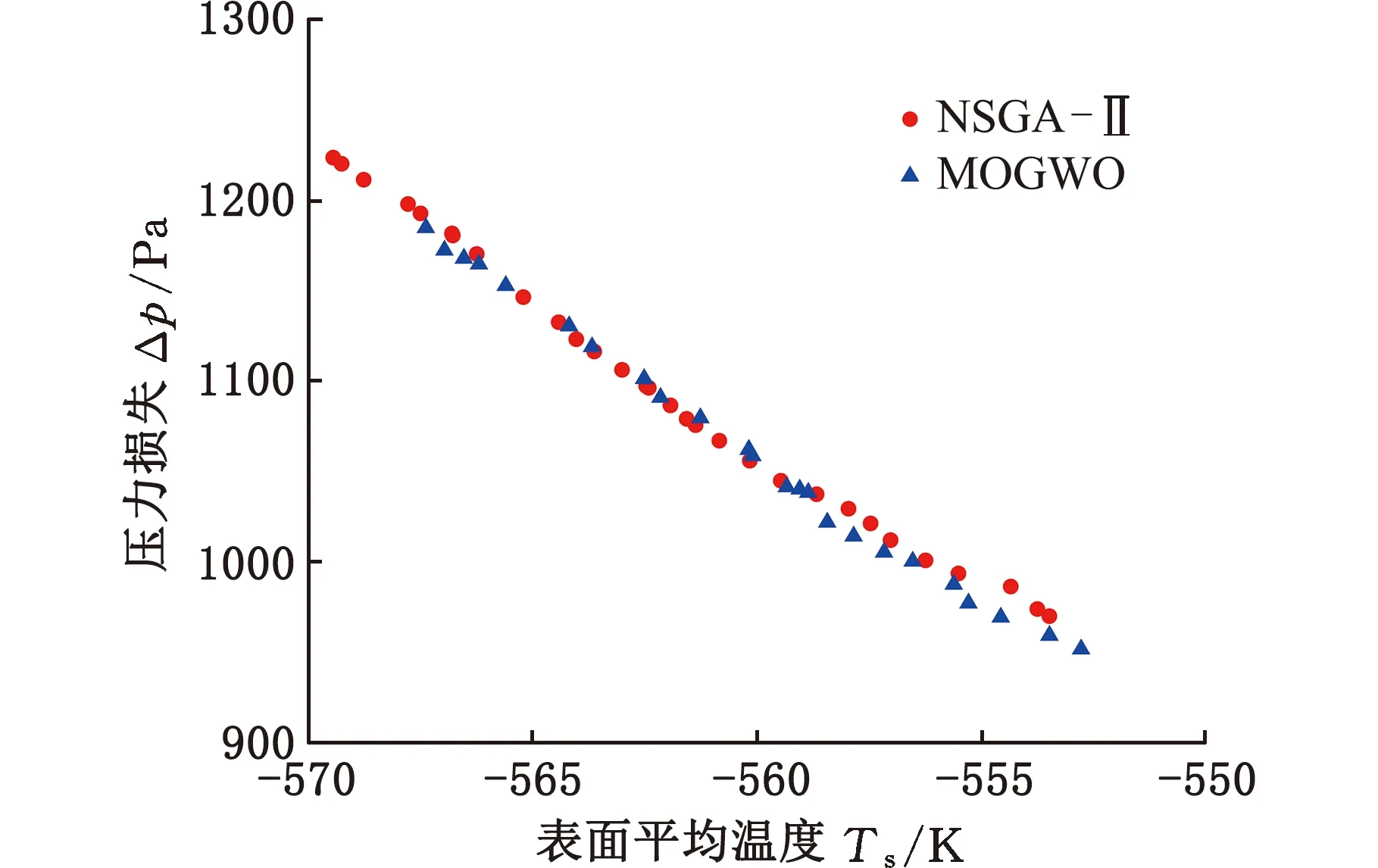
图10 基于NSGA-Ⅱ和MOGWO的优化解集Fig.10 Optimized solution based on a multi-target grey wolf algorithm and non dominated sorting genetic algorithm-Ⅱ

图9为热交换器车载兼容性多目标灰狼优化算法流程图，为了方便计算和搜索，将表面平均温度的目标函数值取负，优化的目标即为表面平均温度和进出口压力损失皆最小。设置多目标灰狼算法中灰狼的种群为100，最大迭代次数为300，外部种群archive为30。同时与经典的非支配排序遗传算法(NSGA-Ⅱ算法)进行对比，NSGA-Ⅱ算法初始种群规模设置为30，最大迭代次数为300，遗传交叉概率为0.9，变异概率为0.25，运行后所得非劣解结果如图10所示。可见，基于多目标灰狼算法所得的Pareto解集与基于NSGA-Ⅱ算法所得的Pareto解集在中间段几乎重合，前者解集相对集中，而后者相对分散。

定义车载兼容性评价指标σ来确定最终优化结果：σ=Tj/T0/(Δpj/Δp0)，其中，Tj为第j个非劣解的表面平均温度函数值，Δpj为第j个非劣解的压力损失函数值，T0为空腔热交换器(即内部无任何翅片)的表面平均温度，Δp0为空腔热交换器的进出口压力损失。通过对同尺寸的空腔热交换器数值计算后，得到T0=545.10 K，Δp0=853.81 Pa，将所有非劣解转换为评价指标σ值。

图11所示为所有非劣解对应的评价指标。可见，基于多目标灰狼算法所得的Pareto解集相比基于NSGA-Ⅱ算法所得的Pareto解集整体质量更高，最高评价指标总体上也更大，使用多目标灰狼算法优化热交换器的结构是可行的。其中，基于多目标灰狼算法所得Pareto解集的第4个解的评价指标最高，所对应的设计变量组合为L=34.19 mm，W=7.04 mm，A=76.9°，S=20.24 mm，优化结果是压力损失为951.54 Pa，表面温度为552.78 K，以同样的参数构建热交换器模型并进行数值模拟，仿真结果为压力损失为936.82 Pa，表面温度为554.61 K，相比优化结果分别相差1.57%、0.33%，误差皆小于2%，再次证明了上述高斯过程回归模型的有效性。

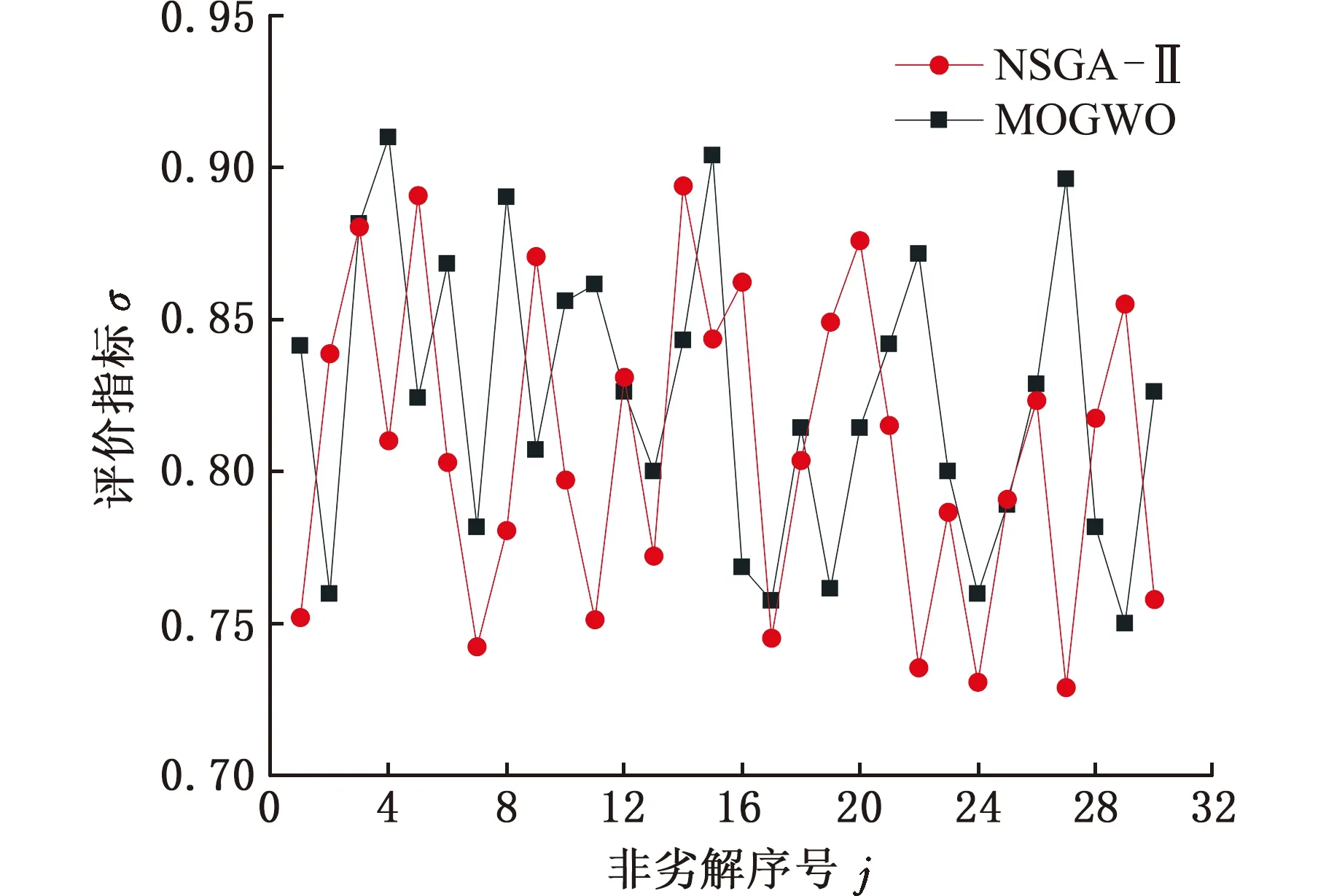
图11 评价指标点线图Fig.11 Evaluation index dot-line chart

图12所示为空腔及上述优化前后热交换器的性能对比。可见，相比同等外部尺寸空腔的热交换器，优化后的热交换器其压力损失从853.81 Pa提高到936.82 Pa(提高了9.72%)，而表面温度从545.10 K提高到554.61 K(提高了1.74%)，虽然压力损失也提升较多，但对发动机的性能影响并不大，在可接受范围内。

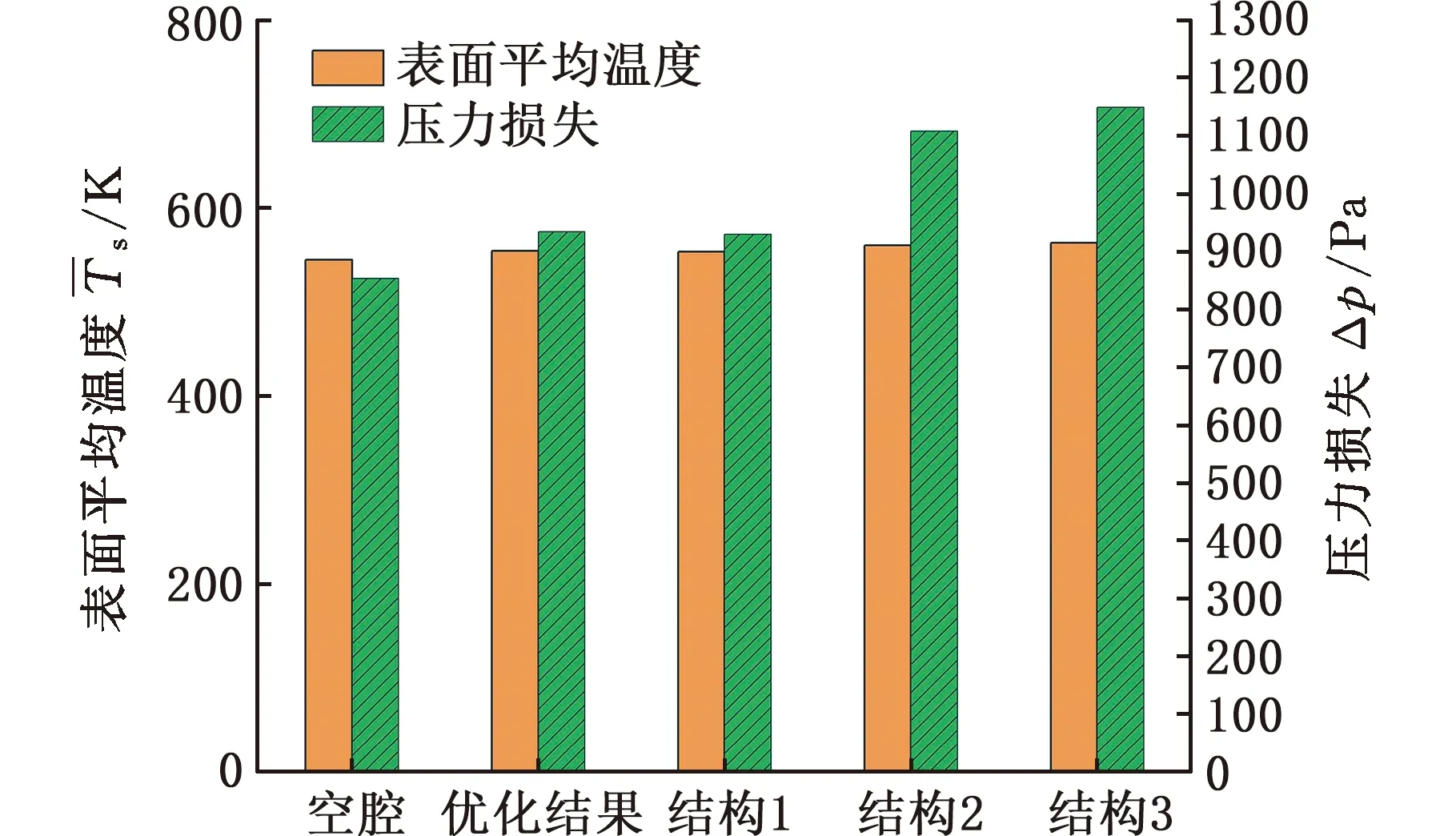
图12 空腔及优化前后热交换器的性能对比Fig.12 Performance comparison of cavity and heat exchanger before and after optimization

此外，上述优化的结构相比结构1，其表面平均温度提高了0.22%，而压力损失提高了0.73%，压力损失的变化也较小，表面平均温度有所提高。同时与结构2和3相比，上述优化结构的热交换器其表面平均温度分别降低了1.01%和1.53%，压力损失分别降低了15.49%和18.50%，热交换器表面平均温度虽然有所降低，但压力损失降低更为显著,对发动机排气的影响更小。

采用40 mm×40 mm×4 mm的热电器件(型号TEHP1-1264-0.8)，在图1所示的六边形热交换器每个面均匀放置5个(共放置30个)。根据塞贝克效应，在接入负载的回路中，当负载电阻和热电器件内阻相等(即负载匹配)时，热电器件的最大输出功率可表示为[16-17]：

Uoc=nαΔT

(13)

(14)

式中，Uoc为热电模块的开路电压；n为热电器件中PN结的数量；α为热电器件的塞贝克系数；ΔT为热电器件的冷热端温差；Pm为热电器件的输出功率；Rm为热电器件的内阻。

根据热电器件厂商(江西纳米克)提供的不同冷端温度下热电器件负载匹配条件下输出功率随热端温度变化的一系列标定性能曲线，利用发动机自身90 ℃左右的冷却水并联通入图1所示的汽车尾气温差发电系统冷却水箱(可假设热电器件冷端温度分布均匀)，取热电器件的热导率为1 W/(m·K)，并以各个热电器件中心点处的温度作为其热端温度，当热交换器入口温度为600 K、入口流速为40 m/s时，假定热电器件冷端温度为100 ℃进行综合考虑，对装置优化前后及空腔热交换器的汽车尾气温差发电系统的发电功率进行仿真，如图13所示。可见，基于上述优化结构热交换器的汽车尾气温差发电系统其最大发电功率较于采用空腔热交换器的系统从23.92 W提高到31.06 W，提高了29.85%。

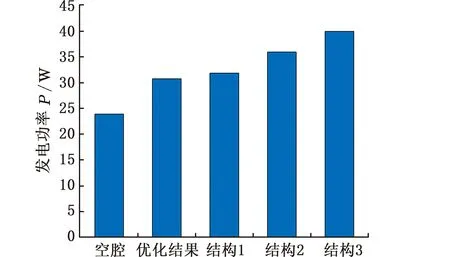
图13 空腔及优化前后温差发电系统发电功率对比Fig.13 Power generation comparison of cavity and thermoelectric generation system before and after optimization

基于上述优化热交换器结构的汽车尾气温差发电系统最大发电功率相比，采用结构1热交换器的系统从30.4 W提高到31.06 W(提高了2.17%)，相比采用结构2和3热交换器的系统分别从35.95 W和38.52 W降低到31.06W(降幅为13.60%和19.37%)，由于其压力损失的显著降低，可认为该优化结构对发动机性能的影响微乎其微。因此，汽车尾气温差发电中很难做到热交换器平均温度更高的同时其压力损失也更小，需要在两者之间进行折中处理，采用上述优化结构热交换器的汽车尾气温差发电系统在兼顾最大发电功率的同时，满足了降低气体背压的车载兼容性要求。

5 结语

回收汽车尾气废热进行发电和车载应用可以进一步提高传统发动机的燃油经济性，降低其排放和污染，而汽车尾气温差发电系统用热交换器的内部流场结构会影响发动机的尾气气流，甚至会恶化发动机的原有性能，这种此消彼长现象造成的车载兼容性差会制约汽车尾气温差发电技术的推广应用。考虑到圆筒式热交换器压力损失相对较小，其表面温度分布更为均匀，本文针对外部形状为六边形而内部为圆筒式的汽车尾气温差发电系统用热交换器提出了正交设计法、高斯过程回归以及多目标灰狼算法结合的优化设计方案，以热交换器表面平均温度最高和进出口两端压力损失最小为优化目标获取了热交换器内部翅片的最优结构参数，优化后的热交换器与结构2和3相比其表面平均温度有所降低，但压力损失降低显著。同时，与空腔热交换器相比其表面平均温度和压力损失皆有提升，但压力损失增幅在可接受的范围内，可忽略不计。因此，通过对热交换器进行优化设计，可以在实现回收尾气废热发电的同时降低其对发动机的影响，达到真正意义的节能减排功效。本文方法是完全有效可行的，为进一步提高汽车尾气温差发电系统的车载兼容性设计及示范应用提供了借鉴。