搅拌摩擦焊机床开放式控制系统及切线跟踪研究
2022-09-03刘立业陈永亮汤伟莉魏云篷索树灿
刘立业 陈永亮 汤伟莉 魏云篷 索树灿
天津大学机械工程学院,天津,300354
0 引言
搅拌摩擦焊(friction stir welding,FSW)是一种固相连接技术,在焊接轻质合金方面有很大优势。由于该工艺是在低于材料熔点的温度下固相中进行的,故焊缝没有收缩、脆化、开裂或孔隙之类的缺陷[1]。该工艺采用一种硬质合金制成的搅拌头,通过主轴的旋转扎入被焊件,随后沿被焊件的焊缝进给,经过搅拌头的搅拌,与工件进行摩擦,使得待焊件温度升高到热塑性状态,高速旋转时材料绕搅拌头从工件前方向后方运动,并在轴肩对工件的挤压的联合作用下,完成了金属间的固相连接[2]。
很多因素都会对FSW焊缝性能产生影响,如旋转速度、焊接速度、焊接压力、搅拌头的形状和尺寸、工艺倾角、倾斜方向等,其中,工艺倾角是搅拌头轴线与工件上表面法线方向的夹角。沿着焊接方向合适的工艺倾角能够确保搅拌头轴肩包容被搅拌针搅拌后的金属材料,可以有效地把这些材料从搅拌针的前端带动到后端,进而对搅拌针后端的金属材料施加压力,形成致密的焊缝[3],合理的倾角对接头的性能及组织结构同样有重要的影响。正是由于焊接倾角的存在,使得在焊接圆弧转弯处,搅拌头要实时进行调节,时刻保持在圆弧的切线方向上,这个功能叫作圆弧切线跟踪。在保证此功能的基础上实现FSW过程变量的检测,建立开放式的FSW控制系统,可以进一步完善FSW工艺并提高焊接质量。
仇晓磊[4]开发出一种平面二维曲线焊接的搅拌摩擦焊设备,采用FAGOR 8055数控系统实现了倾斜方向的跟踪。蔡智亮[5]基于西门子840Dsl数控系统实现了进给轴的运动控制与搅拌头的转速控制,并研究了倾斜方向上非线性误差的补偿算法。夏罗生[6]开发出一种基于PC+PMAC运动控制卡的平面搅拌摩擦焊设备的开放式控制系统,并对搅拌头长度补偿进行了研究。吴功柱[7]针对搅拌摩擦焊设备的设计、焊接过程中下压力的测量以及工艺参数优化等进行了相关研究,并设计了支撑软件。
要实现运动控制与切线跟踪功能,对机床的运动学建模是前提,可以类比五轴机床运动学建模方法。BU等[8]将结合点设置为床身,推导出工件、刀具相对于床身坐标系的变化关系,得到了XYZ-AC式配置的机床运动学模型,通过OpenGL将加工代码变换为刀具运动轨迹。骆海涛等[9]利用机器人学中的D-H法对大型航天搅拌摩擦焊机器人进行了运动学分析,为实现三维轨迹焊接提供了基础。李进进等[10]提出了一种普遍适用于多轴机床的运动学建模方法,并且加入边界条件,增加了求解各种多轴机床运动学模型的准确性。WANG等[11]建立了五轴机床运动学模型库,主要包括五轴机床的几种典型配置,例如刀轴偏置、转台偏置和两者共同偏置。
本文首先构建FSW机床开放式控制系统,再根据D-H法建立机床正逆向运动学模型,并对逆向运动学模型进行验证。最后,设计了一种圆弧切线跟踪方法进行运动仿真与焊接试验,以验证参数化运动学模型的正确性及圆弧切线跟踪方法的可行性。
1 FSW机床开放式控制系统设计
1.1 数控系统的搭建
传统FSW数控系统采用专用计算机系统,软硬件都是封闭的,不仅用户无法重新定义和扩展,也很难满足用户的特殊要求,而且系统缺乏统一、有效和高速的通道与其他控制设备和网络设备进行互联,人机界面不灵活,系统的培训和维护费用昂贵。
为克服传统FSW数控系统的缺点,需要研究开放式的FSW控制系统。开放式数控系统结构主要有以下三种:PC嵌入NC式结构、NC嵌入PC式结构以及全软件型开放式结构。本文采用英国Trio公司的全软型运动控制软件Motion Perfect实现FSW过程中的变量采集、显示及焊接加工,并以此为中心建立了基于Ether CAT的开放式控制系统。
采用以太网将工业计算机与运动控制器相连,控制器与各驱动器之间通过Ether CAT通信,执行机构采用5组交流伺服电机驱动,其中,主轴电机通过万向节与传动轴连接;X、Y、Z轴电机通过减速器与丝杆连接;C轴电机通过蜗轮蜗杆减速器驱动整个主轴转动。测量部分则将各种传感器集成为一体,主要有激光位移、温度、力、扭矩等,系统结构如图1所示。

图1 数控系统结构示意图Fig.1 Schematic diagram of CNC system structure
1.2 数据显示与点动控制界面设计
上位机软件开发在Windows 7操作系统的工业PC中,主要实现与下位机的通信、数据的采集与分析、高级语言开发等。下位机软件利用其中的PLC模块,通过专用语言实现数控系统中的运动控制、误差补偿等实时性要求较高的功能。
采用运动控制软件的界面设计功能,设计一种数据检测与点动控制界面,在焊接过程中实时采集各轴的位置、受力、速度、扭矩等,用户通过为各个点动轴定义运动量、速度及加速度完成点动控制,运动功能通过软件编程语言实现,界面如图2所示。

图2 数据显示与点动控制界面Fig.2 Data display and jog control interface
2 FSW机床运动学建模
对机床进行运动学建模的目的是确定机床各运动构件与末端执行器之间的关系,为控制机床的运动提供分析的方法和手段,为仿真研究机床的运动特性与设计控制器实现预定的功能提供依据。
本文针对龙门式搅拌摩擦焊机床进行运动学建模,机床的结构形式如图3所示。工作台为X轴移动部件,横滑台为Y轴移动部件,主轴箱为Z轴移动部件,机床的B轴和C轴位于刀具侧,起到绕Y轴和Z轴旋转的作用。

图3 龙门式FSW机床结构形式Fig.3 Gantry FSW machine tool structure
2.1 机床的正向运动学
龙门式FSW机床可以看成是由许多连杆组装起来的,这些连杆通过移动或转动的铰链连接,各连杆沿着X、Y、Z轴进行直线运动,或是绕着X、Y、Z轴进行旋转运动[12],根据运动的相对性,把工件视为基座,刀具视为末端执行器,床身、立柱和各部分传动结构看作连杆,构成等效的串联结构[13]。
龙门式FSW机床的等效串联机构如图4所示,其中X0Y0Z0和X6Y6Z6分别是工件固连和刀具固连的坐标系,其余为各运动轴坐标系。考虑真实的焊接情况,用末端执行器处的实线表示初始时刀具方位,虚线表示工作时刀具方位(焊接时搅拌头要绕Y轴旋转一定角度),从而得到相应的连杆和关节D-H参数,见表1。
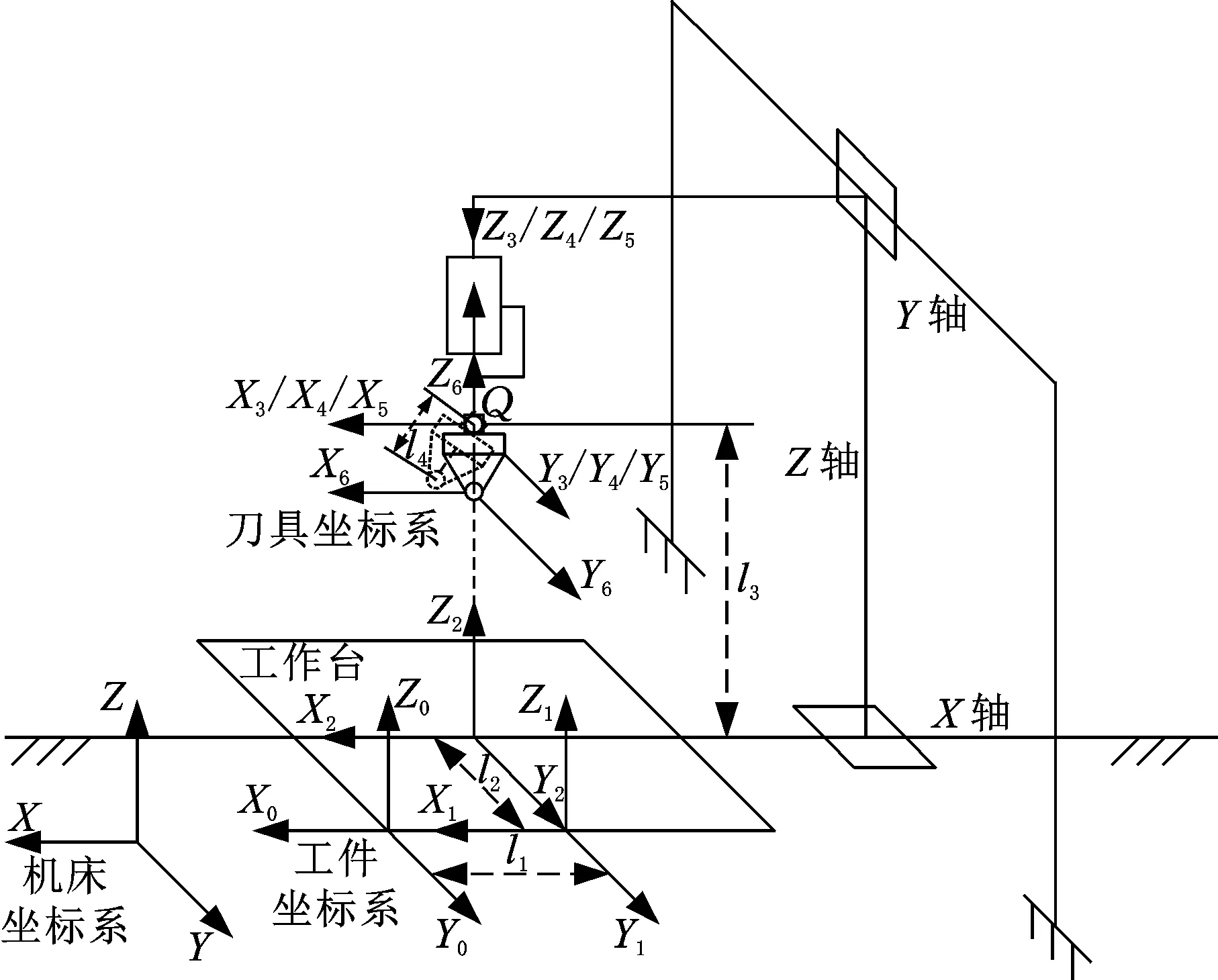
图4 龙门式搅拌摩擦焊机床机构简图Fig.4 Schematic diagram of gantry type FSW machine tool mechanism
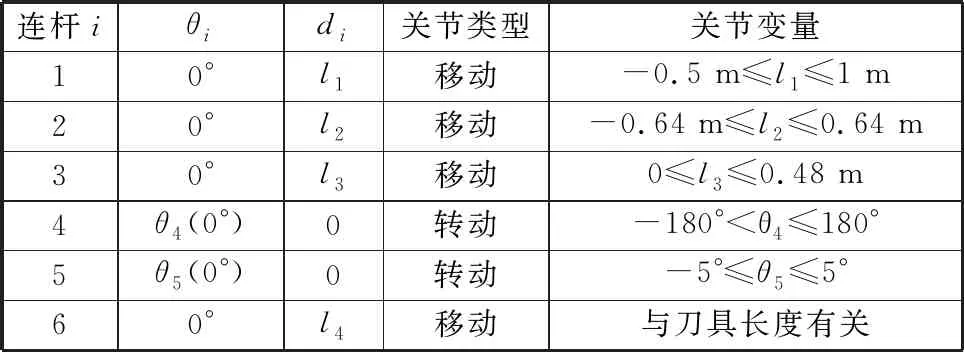
表1 龙门式FSW机床连杆参数和关节变量D-H参数Tab.1 Connecting rod parameters and joint variable D-H parameters of gantry FSW machine tools

(1)
(2)
将表1中的各连杆参数和关节参数代入式(1),得
(5)
(8)
最初在定义坐标系时,不动的部件设定为工作台,移动的部件是床身,而实际加工是工作台移动、床身不动,故从工作台到床身这一段的运动量应该取反(即-l1)。将式(3)~式(8)连乘,得到总变换矩阵:
(9)
式中,s表示sin;c表示cos。

(10)
工件坐标系下的刀轴方向矢量为
(11)
2.2 机床的逆向运动学
工作空间内搅拌头刀具的位姿已知,进而求出铰链空间中变量d1、d2、d3、d4、θ4、θ5的数值叫作运动学逆解。逆向运动学模型求解方法有很多,例如解析法和代数法等[14],本文主要采用代数法,先推导B轴和C轴的运动量,再求出X、Y、Z三轴的运动量。转动轴的运动量为
(12)
移动轴的运动量为
(13)
根据OX、OY的符号也可以确定θ4位于(π/2,π]或(-π,-π/2),当OX<0,OY>0时θ4∈(π/2,π];当OX<0,OY<0时,θ4∈(-π,-π/2)。所以,可以确定θ4的取值范围是(-π,π)。对于θ5,通过arccos函数确定其取值范围是(0,π/2],最后可以通过检测装置来判断B轴的转动方向。
3 圆弧切线跟踪方法
3.1 FSW圆弧切线跟踪
如前文所述,FSW焊接时搅拌头轴线要与工件法线成2°~5°的夹角,以便提供一定的锻造压力,如图5所示。而且当焊接平面圆弧型焊缝时,必须让夹角一直保持在圆弧的切线方向。实现圆弧切线跟踪一般需要在焊接圆弧焊缝时配合一根转动轴的转动,根据龙门式机床的配置形式,本文采用C轴转动的方式进行切线跟踪。

图5 FSW过程中刀具倾斜角度示意图Fig.5 Schematic diagram of tool tilt angle during FSW process
3.2 圆弧切线跟踪实现原理
对于运动控制器,除非其自身带有圆弧切线跟踪功能,否则实现起来较为复杂,本文设计出一种较为简单的圆弧切线跟踪方法,通过计算所焊接圆弧加减速段与匀速段的圆心角和弧长,进而实现圆弧切线跟踪。
运动控制器进行圆弧插补的两根轴需要有相同的加速度、减速度和速度,而且圆弧插补的加减速度和速度与X、Y轴所设置的相同。基本的原理是让C轴转动的加减速度段和匀速度段与圆弧插补的对应段时间相等,即在圆弧插补加减速时C轴转动也在加减速,最终同时完成运动;进而求出C轴转动的加减速度与速度。同时根据圆弧起点终点与圆心坐标计算圆弧所对应圆心角,圆心角与C轴转角有一定的数量关系,当圆弧为优弧时C轴转角等于360°减去圆心角,当圆弧为劣弧时转角等于圆心角。
从以上角度出发,首先求解出圆弧插补的加减速度的时间,其中,a和v分别是圆弧插补的加减速度与速度,其数值与X、Y轴设置相同;其次求出圆弧插补加减速所走的弧长,根据弧长公式求解出加减速段的圆心角φ,根据圆心角和加减速时间可以求解出C轴转动的加减速度;再次根据圆弧插补的加速度时间可以计算出C轴匀速转动的速度;最后进行圆弧插补时同时控制C轴转动相应的角度,以实现圆弧切线跟踪,基本流程如图6所示。

图6 圆弧切线跟踪实现流程图Fig.6 Flow chart of the realization of arc tangent tracking
4 实例
以图7所示的平面二维焊接轨迹为例,验证龙门式搅拌摩擦焊机床运动学模型的正确性和圆弧切线跟踪方法的可行性。

图7 平面二维焊接轨迹Fig 7 Planar two-dimensional welding track
首先取轨迹上9个点编号为0~8,其中,0点为工件坐标系原点,1~8各点相对原点的坐标及C轴的转角情况(逆时针方向为正)已在图7中列出。设定搅拌头运动路径由点0开始按照顺序回到点1结束。在运动过程中刀尖的Z向方位始终保持不变,所以列出各点的刀尖位置和刀轴矢量信息时,PZ的值不再列出。
4.1 FSW机床运动学逆解验证
将龙门式FSW机床三维模型导入Motion Perfect软件中,按照运动学建模时定义的各移动和转动坐标系进行相应设置,如图8所示。其中5个轴的行程分别为:X方向1500 mm,Y方向1280 mm,Z方向480 mm,C方向-180°~180°,B方向-10°~10°。
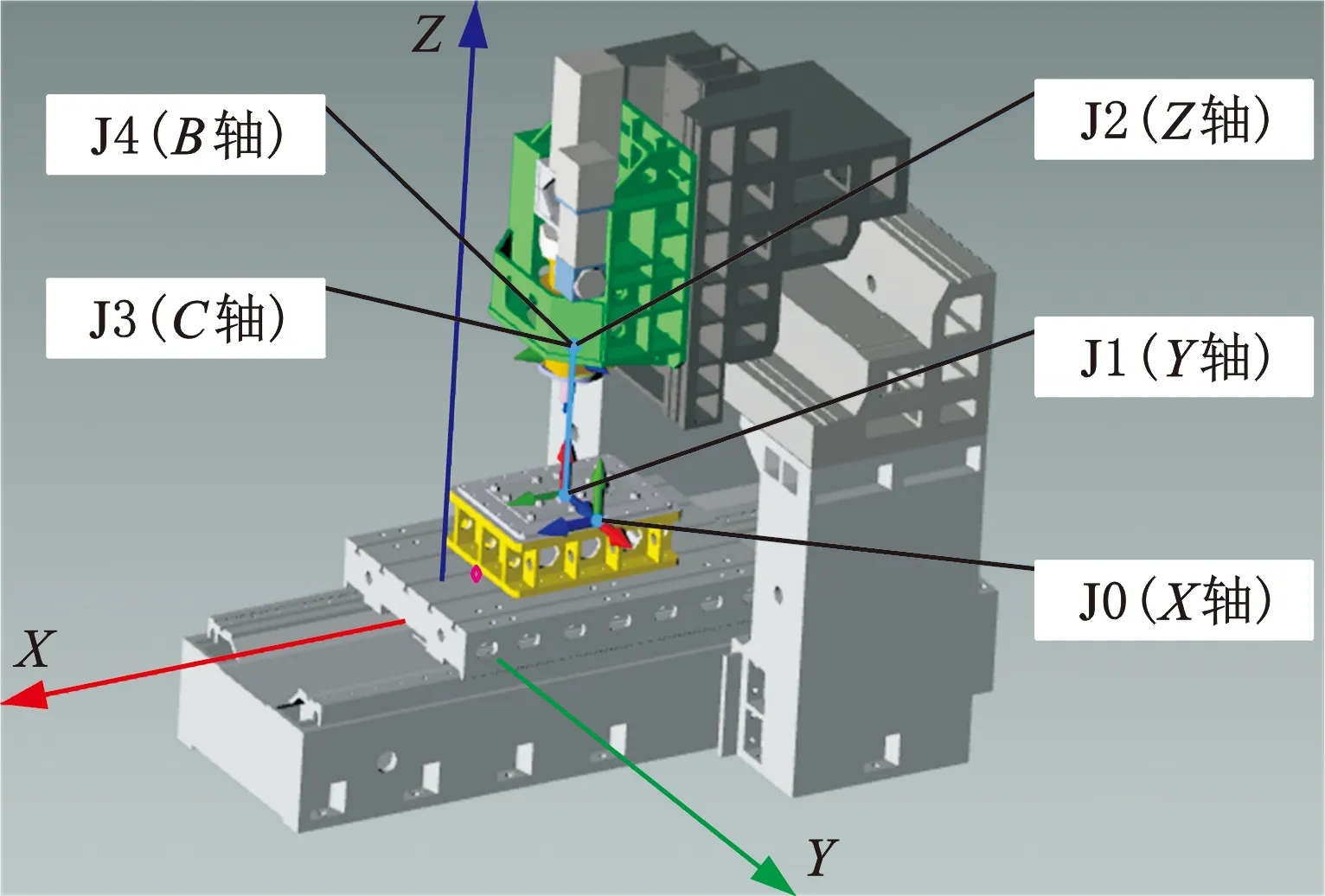
图8 龙门式搅拌摩擦焊机床模型Fig.8 Gantry type FSW machine model
实际焊接时B轴角度固定,由机械结构进行调整,其中,轴J0~J4分别代表X、Y、Z、C、B轴,图8中坐标系为机床坐标系。在运动学建模时已经定义了各连杆关节D-H坐标系位置,再根据设定的机床坐标系位置,可以得到各连杆坐标系相对机床坐标系的位置,见表2。
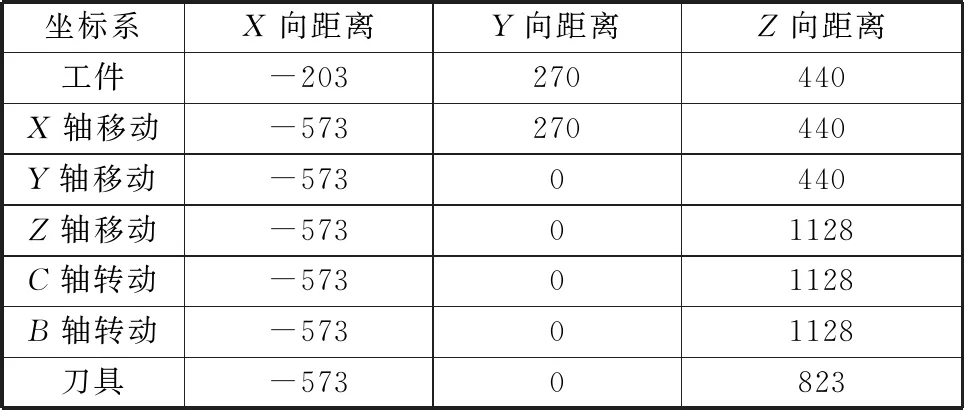
表2 各坐标系相对机床坐标系的空间位置
假设初始状态下刀具坐标系和工件坐标系重合,加工时搅拌头按照实际加工位置运动,使得刀心坐标和方向在工件坐标系中发生变化,根据图5、图7、式(10)和式(11)可以列出各点在工件坐标系下的刀具中心位置坐标和刀轴方位坐标。取l4=-305 mm,θ4=2.5°,见表3。

表3 各点刀尖位置和刀轴矢量信息
根据式(12)和式(13),将各点的坐标代入后得到各点相对于坐标原点的各轴运动量(即运动学逆解),由于在此焊接轨迹下Z轴和B轴是不运动的,故只列出其余3个轴的运动量,见表4。

表4 各轴相对原点运动量
将后一点的运动量减去前一点的运动量即为每一步机床各运动部件的运动量,值得注意的是当C轴摆动角度的符号改变时,计算的每一步运动量需要用360°减去两步角度绝对值的和,方向可以根据圆弧是顺圆或者逆圆确定,见表5。表5中,各轴运动量前的符号代表方向,例如38.5°代表C轴逆时针转38.5°,12.5代表工作台沿X轴正方向移动12.5 mm,24.04代表沿Y轴正方向移动24.04 mm。将所得到的各轴运动量与实例验证的轨迹进行对比,证实了运动学模型逆解的正确性。
4.2 运动仿真
首先参照运动学模型确定各轴运动部件组成、坐标系位置以及坐标原点;然后将运动学模型逆解验证轨迹作为典型工件,编写运动程序;最后运行程序驱动三维模型运动,同时利用软件示波器功能,检测X轴(0轴)、Y轴(1轴)的运动,得到的焊接加工轨迹如图9所示。

表5 每步机床各组件运动量

图9 Motion Perfect中的模拟轨迹Fig.9 Simulation trajectory in Motion Perfect
图9是验证XY轴联动轨迹是否正确,但焊接时还需要C轴的实时转动,C轴的转角情况用曲线表示不太形象,故在3D仿真模型中观察机床的运动情况,选取两段圆弧焊缝上各3个位置观察C轴转角情况,如图10所示。可以看出在完整的圆弧插补过程中,C轴稳定转动,使得搅拌头轴肩开口方向始终沿着圆弧切线,XY圆弧插补及C轴的摆动保证了焊接过程的正确性。
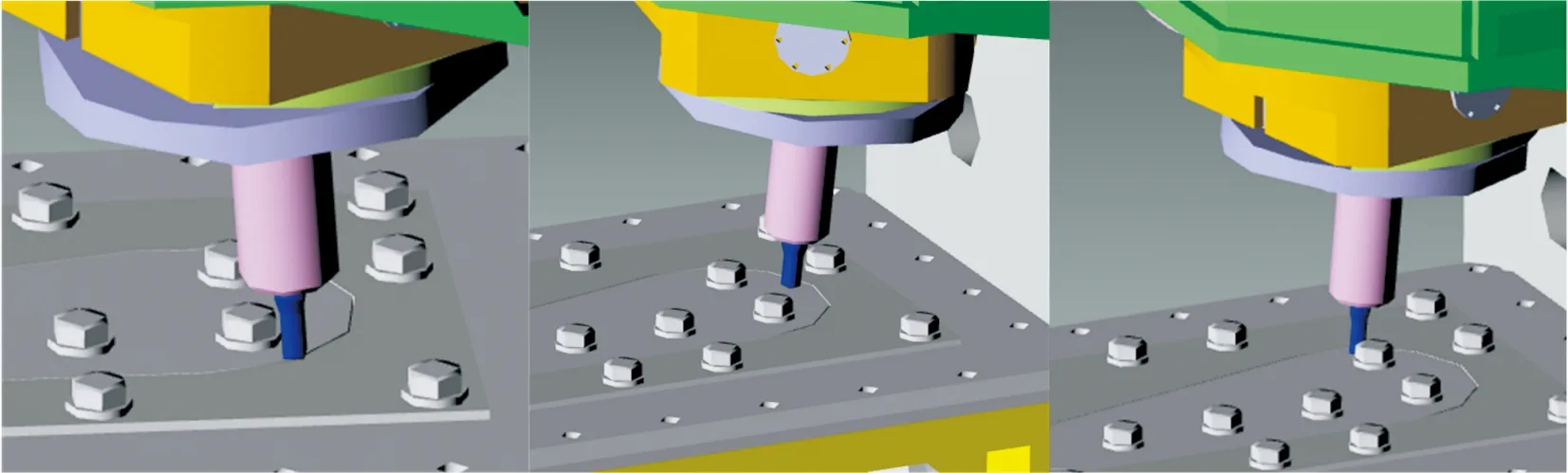
(a)2-5段圆弧转角情况
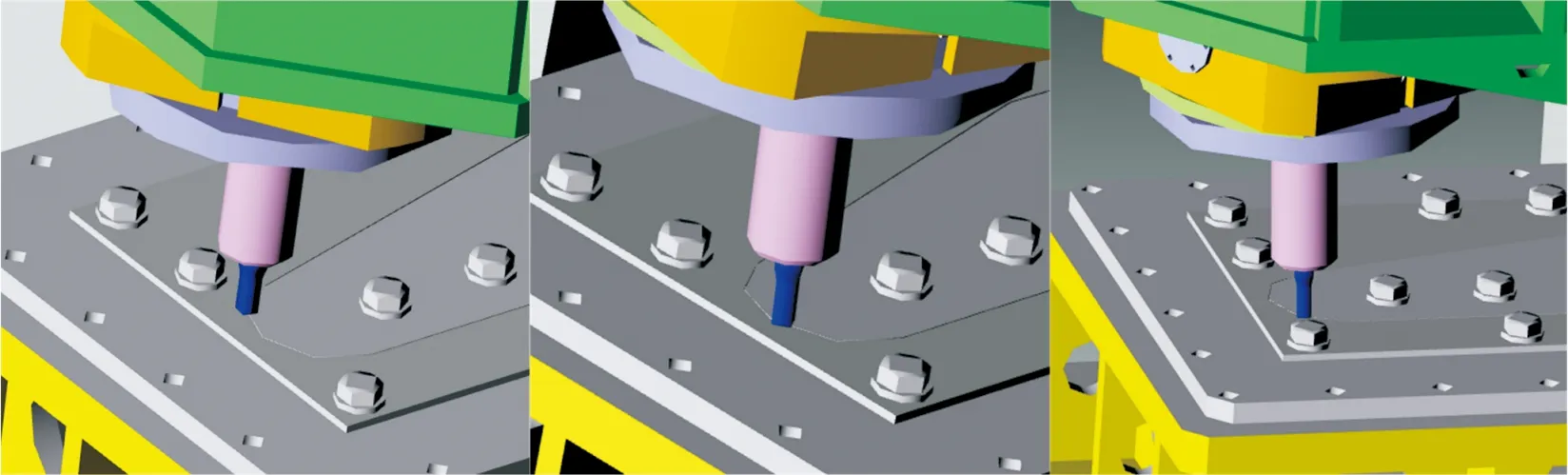
(b)6-1段圆弧转角情况图10 各段圆弧跟踪转角情况Fig.10 Tracking corners of each arc
4.3 实验验证
龙门式FSW机床试验样机如图11所示,利用此样机对图7所示的焊接轨迹进行实验。搅拌头尺寸为8 mm,工件采用5000系列的铝合金板,焊接板厚16 mm,板长500 mm,板宽150 mm,主轴转速600 r/min,进给速度60 mm/min。

(a)外型结构 (b)电器柜结构图11 龙门式FSW机床试验样机Fig.11 Gantry type FSW machine tool test prototype
搅拌摩擦焊在实际焊接时需要将所焊接的工件拼接在一起,然后针对焊缝轨迹编程,本文选择在单一板上进行焊接,是为了验证圆弧切线跟踪方法,首先将试件装卡到工作台上,如图12所示。

图12 试件的装卡Fig.12 The clamping and chucking of the test piece
由FSW工艺可知,焊接温度对焊接质量有着重要的影响。欲得到较好的焊接质量,需要对工件进行充分预热,使其达到一定的温度后再进行焊接。为了监测工件表面温度,在主轴前端安装红外测温仪,温度达到预定温度时开始进给运动,焊接过程中温度的变化情况大致如图13所示,可见,搅拌针插入工件后,随着搅拌针的旋转以及轴肩的压力,工件表面温度升高,最高达307 ℃;预热一段时间后,开始进行焊接时工件表面温度稍有下降,这是由于搅拌头前端稍远位置的工件材料受热比搅拌头中心受热小。最后搅拌头抬出,温度快速降低。

图13 焊接过程温度变化Fig.13 Temperature change during welding
如前所述,当圆弧插补的速度和加速度给定后,C轴转动的速度和加速度就只取决于焊接圆弧半径的大小,当焊接轨迹只有一段圆弧时,C轴的速度不需要改变,但若焊接图7所示轨迹,就需要在焊接到两个不同半径的圆弧时,改变C轴的速度和加速度,加工完成后的工件如图14所示。

图14 轨迹的焊接效果Fig.14 Welding effect of arc trajectory
在焊接过程中,X、Y、Z三轴采用拉绳式的位移传感器测量实际位移,将实际位移与理论位移进行比较,可以得到焊缝的轨迹误差。采样频率为100 Hz,实验测量的实际与理论轨迹如图15所示,X、Y轴实际位移与理论位移的曲线如图16所示。
定量评估轨迹误差的方法有很多种,有平均绝对误差(mean absolute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)等,其计算公式分别为
(14)

(a)实际轨迹
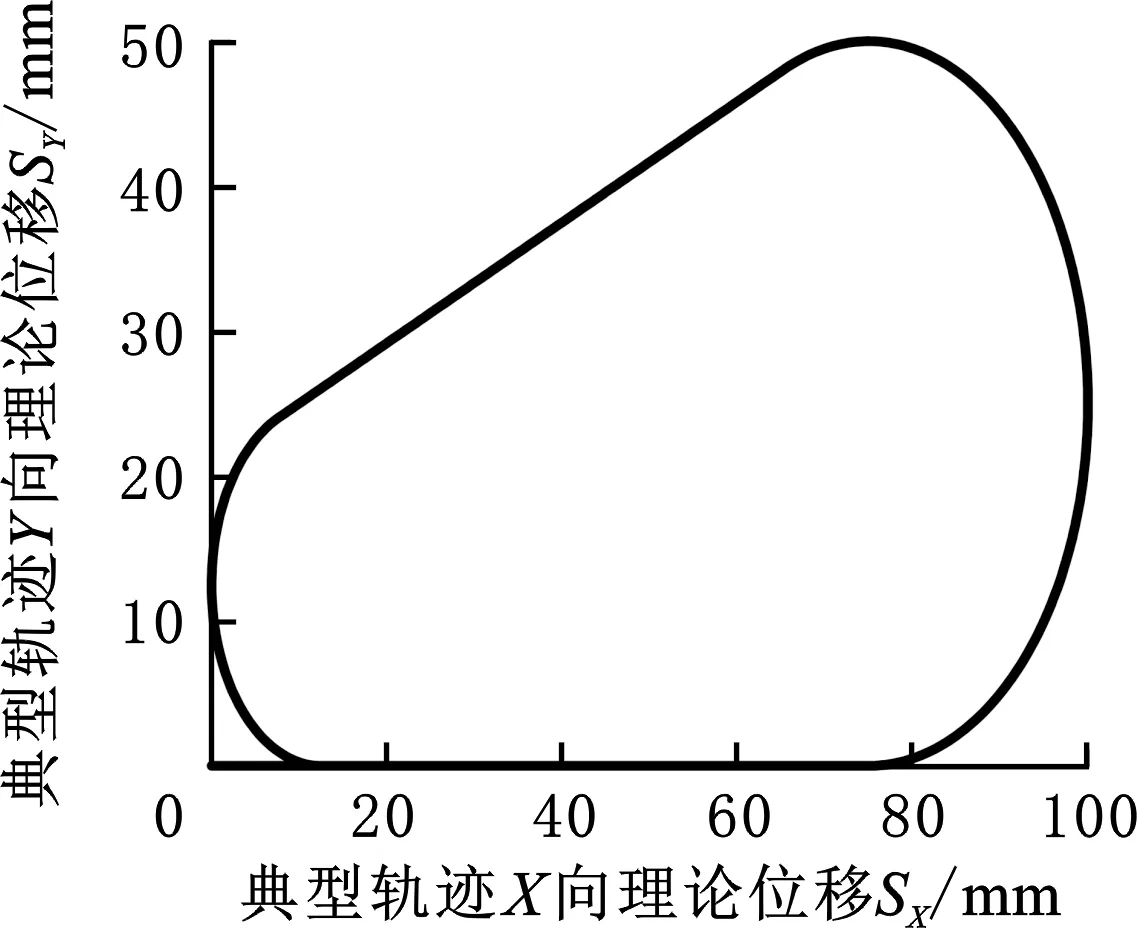
(b)理论轨迹图15 实际与理论轨迹Fig.15 Actual and theoretical trajectories

(a)X轴位移对比 (b)Y轴位移对比图16 X轴与Y轴的理论与实际位移Fig.16 Theoretical and actual displacements of X-axis and Y-axis

(a)MAE值 (b)MAPE值图17 焊接轨迹X向和Y向的MAE值与MAPE值Fig.17 MAE and MAPE of welding trajectory in X and Y directions

5 结论
(1)建立了基于Ether CAT的FSW机床开放式控制系统,采用上位PC+运动控制器+伺服驱动器组成的基于PC的全软型开放式控制系统架构。对焊接过程中的位移、压力、扭矩、转速及温度等信号进行实时监测,为进一步研究FSW焊接工艺打下基础。
(2)建立了龙门式FSW机床的正逆向运动学模型,通过特定的焊接轨迹验证了运动学模型的正确性。设计了圆弧切线跟踪方法,在焊接圆弧段时控制转动轴的转角、速度与加速度,并进行运动仿真,结果表明搅拌头能够实时保持在圆弧的切线方向上,缩短了FSW开放式控制系统的开发周期,节约了开发成本。
(3)针对特定焊接轨迹进行实验,通过红外温度传感器监测焊缝表面温度,指导焊接加工。焊接完成后得到了应用圆弧切线跟踪方法的焊接轨迹误差,并通过不同评价方法对误差进行评估,结果表明利用本文方法的焊接轨迹X向和Y向误差均小于1 mm,平均绝对百分比误差均小于5%。
