考虑大规模直流馈入稳定约束的电网优化调度模型
2022-09-02方珂柯德平孙元章吴浩天沈阳武龚烈锋
方珂,柯德平,孙元章,吴浩天,沈阳武,龚烈锋
(1. 武汉大学电气与自动化学院,武汉430072;2. 国网湖南省电力有限公司电力科学研究院,长沙410007)
0 引言
为了促进西部地区能源资源的充分利用,同时缓解中东部地区能源短缺的现状,我国采用特高压直流输电技术将西部地区富余的能源远距离输送至中东部的负荷中心,从空间上打破了我国能源资源与能源消费逆向分布的状况[1 - 2]。
随着直流输送容量的扩大,直流受端电网受到的影响与挑战也不断加大,受端电网的安全稳定性问题不容忽视。当前,对于直流受端电网的频率稳定问题,主要依靠电网的自身调节(一、二次调频),若没有足够的系统惯量,一旦发生严重故障将造成巨大的损失[3 - 4];对于直流受端电网的电压稳定问题,由于直流一般落点于电网的负荷中心,若缺乏火电机组动态无功支撑,负荷中心的暂态电压将面临严峻的挑战[5 - 6]。为了保证受端电网的安全稳定,在制订运行调度计划时,需要充分考虑直流的输送功率,并开启足够的火电机组以满足频率和电压稳定的要求[7 - 8],即增设一些安稳措施[9]。
另一方面,受端电网自身清洁能源的消纳空间也受到直流输送功率的影响。通常,送端电网根据自身的电力盈余安排直流输送计划,未能考虑到受端电网清洁能源消纳和用电需求,减弱了受端电网清洁能源的消纳能力[10]。
如何在保证受端电网安全稳定的前提下,合理安排机组的启停和出力,优化直流输电的功率,是当前跨区直流运行功率计划制定面临的新问题。文献[11]用等效的N台火电机组叠加以代替直流联络线,并优化等效火电机组的启停,等效于优化直流联络线输送功率,此等效方式使得直流联络线只能在离散的“N档”功率下运行,未能充分发挥直流的灵活调整性。文献[12]充分挖掘了直流联络线与各区域发电机组之间的协调优化空间,提高了直流互联系统的风电消纳能力。文献[13]考虑了多个跨区互联电网之间的输电通道,实现了送、受端电网间的协调调度,促进了新能源在更大范围内消纳。文献[14]综合考虑了风电消纳和受端电网负荷变化,充分发挥了直流联络线的调峰潜力,改善了受端电网的调峰裕度。文献[15]在保证送、受端电网安全运行前提下,优化直流外送计划,但是其中只考虑了一些常规的电网安全约束,未充分考虑直流对受端电网运行计划的影响。文献[16]考虑了直流闭锁等故障对受端电网的影响,优化直流的最优送电容量、机组启停,在充分消纳直流输送功率的同时提高了交直流受端电网运行的安全性。文献[17]考虑了条件控制断面约束,充分考虑了源(送端电网)荷(受端电网)特性,提高了受端电网对直流的吸收能力。
综上所述,现有考虑直流约束的研究常以提升送端电网清洁能源消纳量为目标,较少考虑到受端电网清洁能源消纳的需求以及受端电网为应对直流馈入对火电机组开机方式的要求。不合理的直流送入功率及其与火电机组开机方式的耦合关系挤压了受端电网清洁能源消纳空间,同时造成额外的火电机组开机,不利于兼顾互联电网整体的经济性。
在现有研究成果的基础上,本文紧贴工程实际需求,建立了考虑大规模直流馈入稳定约束的电网优化调度模型。模型综合考虑了送端电网直流外送调整能力与调整代价、受端电网本地清洁能源消纳需求和负荷特性、直流送入功率与火电机组开机台数、备用容量的耦合条件约束,协调优化了直流输送功率、常规电源与清洁能源的计划出力,以保证电网安全稳定运行,兼顾送、受端电网整体的经济效益。
1 考虑大规模直流馈入稳定约束的电网优化调度模型
1.1 优化目标
本文以最小化受端电网火电机组运行成本、直流电费成本、直流额外调整成本为优化目标,如式(1)所示。
(1)
式中:T为调度周期;t为时段编号,t=1,2,…,T;Nm为火电机组台数;i为火电机组编号;Cm,i,t为火电机组i在t时段的运行成本;fDC为直流电费单位成本;pDC,t为t时段的直流输送功率;CDC,t,e为t时段的直流向上额外调整成本。
火电机组运行成本主要包含机组出力产生的燃料费用以及开关机费用,如式(2)所示。
Cm,i,t=cp,i,t+cu,i,t+cd,i,t
(2)
式中:cp,i,t、cu,i,t、cd,i,t分别为火电机组i在t时段的燃料费用、开机费用、关机费用,其计算方式参照文献[18]。火电机组的运行成本决定了其开机顺序,成本较低的机组优先被开机。
1.2 直流联络线运行模式约束
1)模式1:联络线功率按计划运行模式
送端电网根据自身的电力盈余安排直流联络线功率输送计划PlanA, 如式(3)所示。
pDC,t=pDC,t,sche
(3)
式中pDC,t,sche为t时段送端电网安排的直流输送计划。
该模式下不存在直流向上调整的情况,即:
CDC,t,e=0
(4)
受端电网按照PlanA支付送端电网相应的电费,同时根据该计划制定本区域内机组的发电计划。
该模式可以保证送端电网清洁能源的消纳,但是直流运行计划未能考虑到受端电网的负荷特性和运行情况,可能会挤压受端电网本地的清洁能源消纳空间,单方面较友好于送端电网。
2)模式2:考虑受端电网清洁能源消纳的联络线功率优化模式
送端电网根据自身电网运行情况安排直流联络线功率输送计划PlanB, 并提供给受端电网参考。受端电网根据自身清洁能源可发电情况,在PlanB的基础上,优化得到直流的输送计划PlanC, 将PlanC提供给送端电网,并按照PlanC的直流输送电量支付电费和安排本区域内机组的发电计划。值得明确的是,由于需要为受端电网清洁能源消纳提供空间,优化后的PlanC在每一个时段的输送功率都不大于PlanB。 如式(5)所示。
pDC,t≤pDC,t,sche
(5)
该模式下,直流可以向下调整,但同样不存在向上调整的情况,即:
CDC,t,e=0
(6)
该模式考虑了受端电网的清洁能源消纳情况,优先消纳本地的清洁能源,但是该运行模式将使得送端电网的直流送出电量降低,进而影响送端电网的运行经济性。
3)模式3:综合考虑送、受端电网清洁能源消纳与经济性的联络线功率优化模式
送端电网根据自身电网运行情况安排直流联络线功率输送计划PlanD, 提供给受端电网参考。同时送端电网还向受端电网提供与该计划对应的直流向上可调节范围以及相应的额外调整费用(每个时刻的直流向上调节范围与额外调整费用由送端电网根据自身电力调整能力确定)。
受端电网根据自身运行情况,综合考虑本地清洁能源消纳需求与送端电网提供的PlanD、 直流调整范围、额外调整费用,优化得到直流的输送计划PlanE, 将PlanE提供给送端电网,并按照PlanE的直流输送电量支付电费,同时支付直流向上调节部分的额外调整费用。
由送端电网的直流向上调整范围和额外调整费用,可得:
pDC,t≤PDC,t,limit
(7)
(8)
式中:PDC,t,limit为送端电网提供的t时段直流向上调整上限值;gt为t时段送端电网根据其直流调整能力设定的直流向上调整费用系数。
该模式一方面考虑了受端电网的清洁能源消纳需求,另一方面考虑了送端电网直流调整能力,补偿了送端电网直流调整费用,充分发挥了直流联络线功率的灵活性,兼顾了送、受端电网整体的经济性。
1.3 火电机组约束
1)发电功率约束
pm,i,t+Ri,t,w,up+Ri,t,o≤Pi,maxvi,t
(9)
Pi,minvi,t≤pm,i,t-Ri,t,w,down
(10)
Ri,t,w,up,Ri,t,w,down,Ri,t,o≥0
(11)
式中:pm,i,t为火电机组i在t时段的出力;Pi,max、Pi,min为火电机组i的出力上、下限;Ri,t,w,up、Ri,t,w,down为火电机组i在t时段上、下负荷旋转备用容量(本文未考虑负荷的不确定性,该备用为火电机组应对风电出力不确定性增加的旋转备用);Ri,t,o为火电机组i在t时段的旋转事故备用容量(该备用为火电机组应对大规模直流馈入增加的备用);vi,t为火电机组i在t时段的开关机状态,1表示开机,0表示关机。
式(9)—(10)考虑了火电机组的发电能力,对计划出力与备用同时进行约束,保证了风电、火电机组联合调度出力安排的可行性。
2)爬坡约束
pm,i,t-Ri,t,w,down≥pm,i,t-1-SRDivi,t-1-
Pi,max(1-vi,t)
(12)
pm,i,t+Ri,t,w,up+Ri,t,o≤pm,i,t-1+SRUivi,t-1+
SSUi(vi,t-vi,t-1)+
Pi,max(1-vi,t)
(13)
pm,i,t+Ri,t,w,up+Ri,t,o≤Pi,maxvi,t+1+
SSDi(vi,t-vi,t+1)
(14)
式中:SRUi、SRDi、SSUi、SSDi分别为火电机组i的上爬坡速率、下爬坡速率、开机爬坡速率、关机爬坡速率。式(12)—(14)利用相邻两调度时刻的开关机状态变量构造约束,综合考虑了机组组合中火电机组正常爬坡(相邻时段均开机)、开关机爬坡与备用之间的耦合关系。
此外,最小开关机时间约束参照文献[18]中相关内容。
1.4 水电机组约束
对于大型水电站,其水位库容、尾水位发电流量关系可近似成线性关系。同时考虑到在一天内,水库水位与尾水位的水位差变化较小,因此将水头近似为常量。
1)水位库容、尾水位发电流量关系约束
Hj=Fj,H(Vj)
(15)
hj=Fj,h(Qj)
(16)
式中:j为水电站编号;Hj、Vj、hj、Qj分别为水电站j的水库水位、库容水量、尾水位、发电流量;Fj,H(·)、Fj,h(·)分别为水电站j的水位库容、尾水位发电流量关系函数,本文使用一次函数对离散的相关数据进行拟合。
2)水电出力发电流量关系约束
ph,j,t=Kj(Hj,t-hj,t)Qj,t
≈KjHj,consQj,t
(17)
式中:ph,j,t为水电站j在t时段的出力;Kj为水电站j的综合出力系数;Hj,t为水电站j在t时段的水库水位;Hj,cons为水电站j的水库水位与尾水位之差,即水头,在一天内近似为常量;Qj,t为水电站j在t时段的发电流量。
此外,梯级水电站的发电流量、出库流量、水位、始末水位、水量平衡、出力等约束参照文献[19 - 20]中相关内容。
1.5 风电机组约束
1)风电出力约束
pw,k,t≤pw,k,t,predicted
(18)
式中:k为风电场编号;pw,k,t、pw,k,t,predicted分别为风电场k在t时段的调度值、预测值。
2)考虑风电不确定性的备用约束
(19)
(20)
式中:Nw为风电场数量;pw,k,t,down为风电场k的t时段在90%置信水平下的预测误差概率分布的下边界;式(19)—(20)为火电机组为应对风电出力的不确定性设置的备用,即当风电实际出力小于调度值时,由火电机组上备用容量弥补该部分能量的缺失;当风电实际出力大于调度值时,由火电机组下备用容量降出力运行,为风电消纳提供空间[21 - 22]。
1.6 直流联络线安全稳定约束
为了保证受端电网的安全稳定运行,当直流输送功率处于不同区间内时,受端电网需要相对应开启足够数量的火电机组和预留足够的旋转事故备用容量。该耦合关系如式(21)所示。
(21)
式中:y为直流联络线输送功率区间编号,y=1,2,…,n;n为直流输送功率区间数量;Nopen,y、Ro,y、PDC,y分别为直流联络线在第y个输送功率区间内对应的火电机组最小开机数量、火电机组最小旋转事故备用容量、输送功率区间边界值。
该约束为多段逻辑约束,与常规的if-then型逻辑约束相比,其形式上更加复杂、求解难度更大。可使用Big-M[23]法将其线性化,通过引入整数变量,将该逻辑约束松弛解耦。对于任意一段逻辑约束,如式(22)所示,可转换成如式(23)所示的线性约束。

(22)
(23)
式中:My,1、My,2、My,3为绝对值较大的数;zy,t为0-1整数变量,表示直流在t时段是否处于该功率区间内;ε为严格不等式的精度参数。
另外,在t时段直流功率只能处于其中1个条件区间内,即对应其中1个火电机组最小开机数量和最小旋转备用容量,因此需要保证联络线功率档位的互斥性,引入式(24)。
(24)
引入式(23)—(24)后,通过松弛解耦得到的混合整数线性约束与原多段逻辑约束等价,这大大降低了优化算法对该类约束的求解难度,同理,式(8)可以参照此方法处理。
1.7 潮流约束
大规模电网的交流潮流计算十分繁杂,为了保证求解的速度,本文采用直流潮流计算方式,将非线性电力系统潮流问题转化为线性问题[24]。
1)线路容量约束
(25)
式中:l为省内主要传输线编号;Nh为水电站数量;b为负荷节点母线编号;Nbus为负荷节点母线数量;Sl,m,i、Sl,h,j、Sl,w,k、Sl,load,b分别为火电机组i、 水电站j、 风电场k、 负荷节点母线b对应于传输线l的直流潮流传输系数;Sl,DC为直流联络线传输系数;Pload,b,t为母线b在t时段的负荷预测值;Pl,max、Pl,min为第l条传输线的正、反向输送功率极限。
2)功角约束
直流潮流成立的前提为传输线两端节点功角之差足够小,因此引入节点功角约束,如式(26)—(27)所示。
Bnodeθ=P
(26)
(27)

1.8 功率平衡约束
(28)
式中:pelse,t为不参与优化的小火电、水电等电源在t时段的出力。本文将其视作已知常量。
本文在建模过程中对各种非线性因素进行了可行的线性化处理,建立了考虑大规模直流馈入稳定约束的电网优化调度模型,分析可知该模型是混合整数线性规划(mixed integer linear programming, MILP)模型,可直接采用CPLEX进行求解。本文利用CPLEX 12.10求解器进行求解,软件环境为MATLAB2014b, Intel Core i7-8700。
2 算例分析
本文基于国内某省网典型日的实际数据进行计算分析。
2.1 省网系统基础数据
该省网参与优化调度的发电单元包含37台火电机组、10个梯级水电站、47个风电场。其他发电单元,如地调小火电、小水电等,其数据使用典型日的实际值。研究的网架结构为220 kV及以上线路,共包含489个节点。该电网作为受端电网,通过一条直流联络线与送端电网相连。直流联络线的功率与省内火电机组的最小开机台数、最小旋转备用容量的关系详细要求如表1所示。火电机组的运行费用参数参照文献[25]。直流联络线电费单位成本为75 美元/MWh。模型共含24 190个变量,共计60 196条约束,规模庞大。

表1 直流联络线对火电开机数量及旋备要求Tab.1 Requirements for the number of power-on units and spin-up of thermal power plants by HVDC tie-line
2.2 典型日系统运行情况分析
图1所示为典型日内该省网系统各发电单元的出力情况。可以看到,直流在负荷低谷时期送入功率较低,负荷高峰时期送入较高,起到了一定的调峰的作用,缓解了受端电网的调峰压力。同时不难发现,该省网的水电较多,支撑了25%左右的用电量,调峰的压力也主要由火电和水电两个发电单元承担。一方面,在负荷高峰时段(12:00—24:00),主要由火电机组承担该时段的向上调峰压力,考虑到火电机组的发电成本会随着发电量的增加而迅速增加,因此火电机组承担的向上调峰压力越大,系统运行代价相应的增加越多。另一方面,在负荷低谷时段(2:00—10:00),主要由梯级水电站承担该时段的向下调峰压力,导致部分水能无法充分利用,出现弃水的情况,造成了清洁能源的浪费,进一步降低受端电网的经济性。

图1 典型日系统发电单元出力情况Fig.1 Typical daily system power generation unit output
总而言之,受端电网调峰资源和手段的不足限制了其清洁能源的消纳和经济性的提升。但是直流作为可以灵活调节的资源,并没有充分发挥其灵活性,送端电网是否能够在其可调节范围内,调整直流的功率,为受端电网提供更合适的直流送入功率;此外,受端电网在得到更优质资源的同时,能否让利于送端电网,对其直流送出功率的调节进行补偿,以兼顾送端与受端整体的经济性。
2.3 直流联络线计划优化运行情况分析
为了验证本文所提考虑大规模直流馈入稳定约束的电网优化调度模型与直流联络线功率优化模型的有效性,本文在1.2节所述的直流3种运行模式下分别计算,并对计算结果进行对比分析。
2.3.1 直流联络线计划与优化运行曲线分析
直流联络线3种运行模式下功率曲线对比如图2所示。

图2 直流联络线功率优化曲线Fig.2 Optimized curves of HVDC tie-line power
对比图2与图1可以看出,在模式1中,直流计划输送功率整体上与负荷走势类似,在一定程度上满足受端电网的调峰需求;在模式2中,考虑了受端电网的清洁能源消纳需求,可以看到,在负荷低谷时段02:00—09:00,直流联络线优化功率降至最低输送功率,为受端电网本地清洁能源消纳提供空间,在负荷高峰时段,直流仍然保持原输送计划不变;在模式3中,综合考虑送端电网的可调节能力,直流优化功率在负荷低谷时段同样降至最低出力,在负荷高峰时段,直流优化功率向上调整,进一步缓解受端电网的调峰压力。
2.3.2 受端电网等效负荷峰谷差分析
直流联络线以计划和优化运行的等效负荷峰谷差及峰谷差率如表2所示。
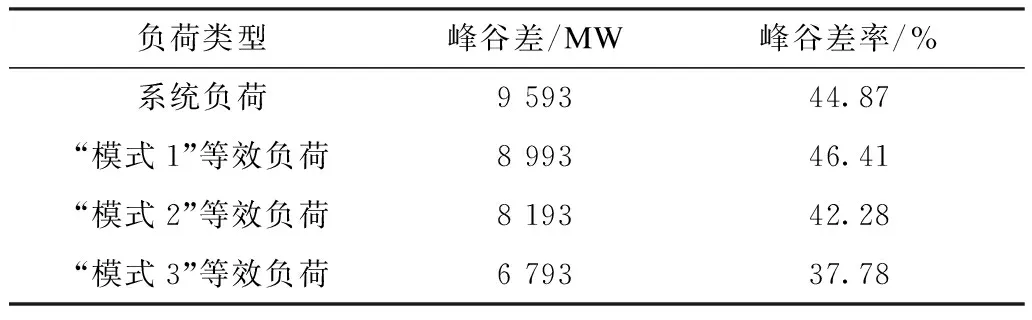
表2 受端电网负荷峰谷差率Tab.2 Peak-valley difference rate of load in receiving-end power grid
由表2可知,系统原负荷的峰谷差为9 593 MW,峰谷差率达到了44.87%。直流的馈入在一定程度上可以起到“移峰填谷”的效果。随着直流运行模式由“模式1”至“模式2”再至“模式3”,系统等效负荷的峰谷差和峰谷差率整体呈现下降趋势,这表明,受端电网的调峰压力在不断降低。进一步说明,越合理的直流输送功率越可以缓解受端电网的运行压力。
2.3.3 送、受端系统运行经济性与清洁能源消纳量对比分析
对于综合考虑送、受端电网清洁能源消纳与经济性的联络线功率优化模式,其直流功率可调节上限、调整费用系数、直流优化功率如图3所示。模式1、模式2与模式3的受端系统运行成本、清洁能源消纳电量与直流电量如表3所示。

图3 考虑调整上限与调整代价的直流功率优化曲线Fig.3 Optimized curves of HVDC power considering adjustment upper limit and adjustment cost
由图3可以看到,直流优化功率在送端电网提供的可调节上限以内,满足了送端电网直流可调整的限制。在01:00—10:00时段,送端电网直流可调节上限较高,表明其可调节能力强,相应的直流调整费用系数较低,而此时段受端电网对直流向上调整需求不高,优化后的直流功率大多处在计划功率之下;在11:00—24:00时段,送端电网直流可调节上限降低,表明其可调节能力减弱,相应的直流调整费用系数较高,而此时受端电网对直流向上调整的需求较高,优化后的直流功率大多处在计划功率之上,受端电网若希望在该时段向上调整直流的送入功率,则需要花费相对较大的调整代价。
由表3可以看到,对于上述3种直流运行模式,在受端系统运行总成本方面,模式1的运行总成本最高,且在受端电网清洁能源消纳量方面,其消纳量也最低,结果表明这种根据送端电网电力盈余安排的直流联络线计划功率,在一定程度上增大了受端电网的运行成本,阻碍了清洁能源的消纳。

表3 受端系统运行成本、清洁能源消纳电量、直流调整成本与电量Tab.3 Operation cost of receiving-end power grid, accommodated power of clean energy, adjustment cost and power of HVDC
当考虑受端电网清洁能源消纳需求后,对直流联络线功率进行优化(模式2),我们发现,受端电网的运行成本由1.446 3×107美元降低至1.396 2×107美元,同时,受端电网的清洁能源消纳量也有所提升,可见,该模式相对友好于受端电网。然而,仍需注意的是,该模式下的直流送入总电量由模式1的4.38×104MWh降低至3.70×104MWh,显然,直流总电量的降低,会直接影响送端电网的经济效益。
可见模式1相对友好于送端电网,模式2相对友好于受端电网,难以兼顾送、受端电网的经济性。因而,本文提出了模式3的直流运行模式,既考虑了受端电网的清洁能源消纳需求,同时又考虑了送端电网直流调整能力与代价,旨在模式1与模式2的基础上寻求送、受端电网的双赢。
由模式3的运行结果,可以看到,受端电网系统的运行总成本进一步降低,相对于模式1,总成本降低了6.91×105美元,其中,总成本包括了支付给送端电网的8.386×104美元的直流调整成本,受端电网在运行成本降低的同时,送端电网同样可以得到经济性的补偿。在清洁能源消纳方面,直流优化后(模式3),受端电网的清洁能源消纳量进一步提升。值得一提的是,在直流送入总电量方面,相对于模式1,模式3的直流总电量也得到了进一步提升,送端电网可以获得更多的直流电费。总的来说,本文所提的直流优化模式3,降低了受端电网的运行成本,促进了受端电网清洁能源消纳,补偿了送端电网的直流调整代价,提升了直流送入总电量,兼顾了送、受端电网的经济性。
2.3.4 直流联络线功率与受端电网开机数量(稳定约束)分析
为了保证受端电网的安全稳定运行,在直流输送功率处于不同区间内时,要求受端电网开启足够的火电机组并预留足够的旋转备用容量。直流联络线在上述3种模式下的运行功率与受端电网开机数量分别如图4—6所示。

图4 模式1直流功率与受端电网开机数量Fig.4 HVDC power in mode 1 and the number of startup units in the receiving-end power grid

图5 模式2直流功率与受端电网开机数量Fig.5 HVDC power in mode 2 and the number of startup units in the receiving-end power grid

图6 模式3直流功率与受端电网开机Fig.6 HVDC power in mode 3 and the number of startup units in the receiving-end power grid
综合图1与图4可以看到,当直流联络线以“模式1”计划运行时,在负荷低谷的02:00—09:00时段,火电机组以最小开机34台运行,然而,在负荷高峰的部分时段(13:00—14:00、21:00—24:00),实际开启的火电机组数量比最小开机数量多了1台。
综合图1与图5可以看到,当直流联络线以“模式2”计划运行时,考虑到受端电网清洁能源的消纳需求,在负荷低谷的02:00—09:00时段,直流输送功率低于“模式1”下的输送功率,直流功率的降低,受端电网稳定约束降级,使得受端电网可以少开1台火电机组,进一步为受端电网清洁能源消纳提供空间;在负荷高峰的部分时段(21:00—24:00),该模式下火电机组的实际开机数量同样比最小开机数量多了1台。
值得明确的是,受端电网火电机组最小开机数量是由直流送入功率决定的,实际开机数量是由受端电网运行情况决定的。通过对比分析图4和图5可知,在负荷低谷时段可以通过降低直流的输送功率,使得受端电网稳定约束降级,进而减少火电机组的开机数量,为受端电网清洁能源就地消纳提供空间;同样,在负荷高峰时段火电机组实际开机数量比最小开机数量多1台,受端电网稳定约束可以升级,即直流送入功率的上限提升,这意味着,可以通过提升直流送入功率,缓解受端电网部分调峰压力,同时也可以提升送端电网的直流送入电量。通过以上分析,可以明确直流输送功率具有一定的优化空间。
综合图1与图6可知,当直流联络线以“模式3”运行时,火电机组的实际开机数量与安全稳定约束要求的最小开机数量一致,没有额外的火电机组开机需求。在负荷低谷时段,火电机组的实际开机数量与直流联络线的输送功率均处于较低水平,为受端电网本地清洁能源消纳提供空间;在负荷高峰时段,开机数量与输送功率处于较高水平;从整体上看,火电机组的实际开机数量与直流联络线输送功率的变化趋势一致,共同承担了系统的调峰任务。结果表明,“模式3”的直流功率兼顾了运行的经济性与受端电网的安全稳定性。
3 结语
本文针对直流受端电网安全稳定与清洁能源消纳的工程实际问题,建立了考虑大规模直流馈入稳定约束的电网优化调度模型。该模型综合考虑了送端电网直流可调整能力与调整代价、受端电网直流馈入的稳定约束、清洁能源消纳需求,充分发挥直流的灵活可调整性,挖掘直流与受端电网各发电单元之间的协调优化潜力,得到合理的直流优化功率以及受端电网的优化运行计划。基于实际省级电网运行数据,验证该模型降低了受端电网的调峰压力,促进了受端电网清洁能源的消纳,降低了受端电网运行成本的同时补偿了送端电网的直流调整成本,提升了直流输送电量,实现了送端、受端电网的双赢,兼顾了送端、受端电网整体的经济性。
