惯导GNSS-RTK可靠性及精度损失规律分析
2022-09-02任续超姚睿
任续超,姚睿
(陕西能源职业技术学院,陕西 咸阳 712000)
1 引 言
目前GNSS-RTK技术在工程建设领域应用非常广泛,传统的RTK测量要求测点过程中对中杆必须对中整平,但实际工作过程中受地形环境等外界条件的影响导致在测量过程中无法在需要测量的点位上进行对中整平测量,因此无法精确获取这些点位的坐标数据。很早之前就有人提出了倾斜测量的理念,也有众多学者对此进行了一系列的理论研究,主要是关于实现RTK倾斜测量的理论可行性和算法研究,惯导系统与GNSS-RTK测量技术的结合,基本实现了RTK动态倾斜测量。目前的惯导GNSS-RTK一般匹配了IMU惯导技术[1],由测量倾斜角的加速度计和测量物体角速度的陀螺仪两部分传感器组成,其中加速度计可以实现对中杆倾斜角度的测定,陀螺仪可以实现对中杆倾斜方向的测定,进而实现了在倾斜测量过程中的坐标改正和高差改正。但受外界环境和传感器自身的缺陷影响,改正值在理论上存在误差,因此就惯导RTK在使用过程中倾斜对其测点精度影响规律以及对工程建设的影响而言,还需要对其测量过程的点位精度做进一步的分析和研究,总结其中的规律,以便更好地服务实际生产。
2 惯导RTK测量原理
在三维直角坐标系中,常规GNSS-RTK观测时处于对中整平状态,可以测出对中杆底部点位的坐标、高程数据,当对中杆倾斜时,所测数据为机头所在位置的平面坐标数据及减去杆高的高程值,原理图如图1[2]。

图1 GNSS-RTK倾斜测量原理图
根据图1可知对中杆杆高为L,RTK倾斜角度为β,对中杆倾斜时测出的数据为(x′,y′,h′),水平状态时测出的数据为(x,y,h),惯导RTK中的加速度计可以测定出对中杆倾斜的角度β,陀螺仪可以测定出倾斜方向确定角度α,进而可以通过数学关系推导出水平状态时的坐标值,图中角θ=(180°-β)/2,计算公式如下[1]:
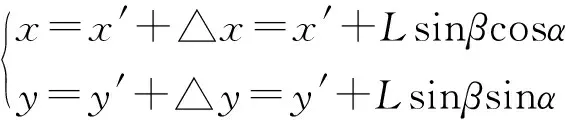
(1)
高程改正值主要和对中杆的倾斜角度有关,水平状态下测得高程为A点高程值h,杆高不变的情况下,对中杆倾斜测量出的为B点高程值h',A、B两点间高差为△h,可知h=h'+△h,由此可得高程改正式如下:
h=h′+△h=h′+L-Lcosβ
(2)

(3)
3 倾斜测量对平面点位精度影响分析
根据倾斜改正公式可知对改正值有影响的因素主要为杆高、倾斜角度以及倾斜方向。结合实际情况主要分三类情况进行实验,验证实际工作中倾斜测量的可靠性及精度损失规律。第一类情况为倾斜方向和倾斜角度相同、杆高不同;第二类情况为倾斜方向不同、倾斜角度和杆高相同;第三种情况为倾斜角度不同、倾斜方向和杆高相同[1]。实验仪器选用千寻SR6型惯导RTK,实验所有数据均为同一基点,基点坐标高程数据为:x=3803642.091,y=565334.395,H=383.98。
3.1 倾斜测量时杆高对测点平面精度的影响
分别以北、东、南三个方向为倾斜方向,倾斜角度分四次变换取值分别为:15°、30°、45°、55°,在各倾斜角度条件下分别测量杆高为 1.4 m、1.5 m、1.6 m、1.7 m、1.8 m、1.9 m、2.0 m时的坐标和高程数据[1],每次测量观测时间为 10 s,间隔时间为 5 s,根据实验设计测得倾斜方向为正北方向的实测数据如表1所示。

表1 倾斜正北方向外业观测数据表
以杆高为横轴,点误差为纵轴绘制不同倾斜角度时的变化曲线如图2所示。

图2 杆高对测点精度影响图
根据图2四种情况可以看出,倾斜测量时点位误差随着杆高的增大有逐步增大的趋势,根据线性回归分析得出a、b、c、d四种情况R2分别为 0.884 2、0.979 9、0.831 9、0.909 6,且斜率均基本接近于0.05,均基本符合线性特征。因此,在倾斜角度一定的条件下,杆高越高点位误差越大,根据表1数据分析,倾斜角度为15°,杆高为 1.4 m的点位误差为 0.039 m,随着杆高和倾斜角度的增大,点位误差也随之逐渐增大,当倾角为15°,杆高增大至 1.8 m时,点位误差达到 0.049 m,根据RTK常规测量的精度要求,一般测点精度需要控制在 5 cm之内。从理论上看,杆高的变化和倾斜角度的变化对倾斜状态的影响有一个共同特点,即倾斜水平偏距的影响,也就是接收机倾斜位置距离竖直状态位置的水平距离。因此,根据表1数据可以初步看出,利用惯导RTK进行倾斜测量时,测点精度若想达到 5 cm以内,就需要将倾斜的偏距控制在 46.6 cm之内。
3.2 倾斜测量时倾斜方向对测点平面精度的影响
惯导RTK在进行倾斜测量时,倾斜方向主要由陀螺仪来进行判断[6],并提供方向参数计算改正值,根据陀螺仪的工作原理初步推测倾斜测量与倾斜方向有关,因此以相同的实验方法测量对中杆倾斜正南和正东方向时的观测数据,从上节可知偏距是影响倾斜测量点位精度的主要因素,因此以偏距为横轴,点位误差为纵轴绘制关系曲线如图3所示,探讨不同倾斜方向测量时的点位误差变化趋势。
根据图3可以看出当对中杆倾斜方向为正北或正南时,偏距与点位误差呈现出明显的线性关系,其R2均在0.9以上,具有较显著的变化规律,而倾斜方向为东方向时,点位误差随着偏距的增大出现起伏变化,且未呈现出明显的变化趋势,当倾斜方向为正南正北时,陀螺仪在进行倾斜方位判定和平面坐标改正数据上存在明显的规律性,在实际工作中可以通过控制偏距来控制精度,而在其他方向无法通过控制影响因素控制测点精度,因此实际倾斜测量时尽可能将对中杆向南北方向倾斜。

图3 不同倾斜方向偏距对点位误差的影响图
3.3 倾斜测量时倾斜角度对测点平面精度的影响
以表1的观测数据作为实验数据,对比相同杆高,倾斜角度不同的点位误差,取四组杆高观测数据,其中包含杆高为两端和处于中间的数据,以倾斜角度为横轴,点位误差为纵轴绘制关系曲线如图4所示。
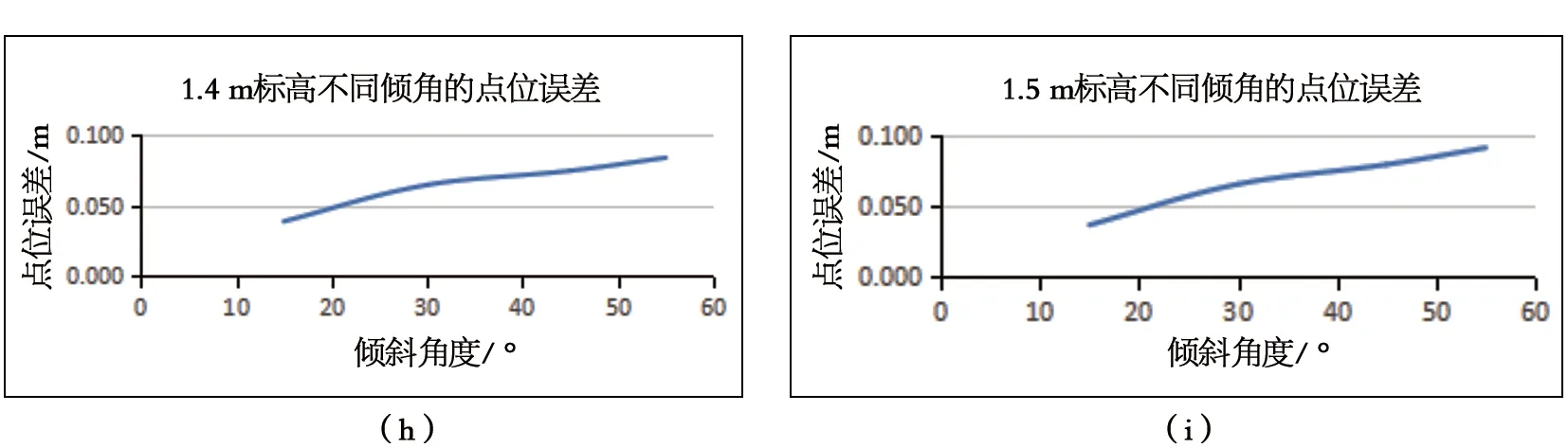
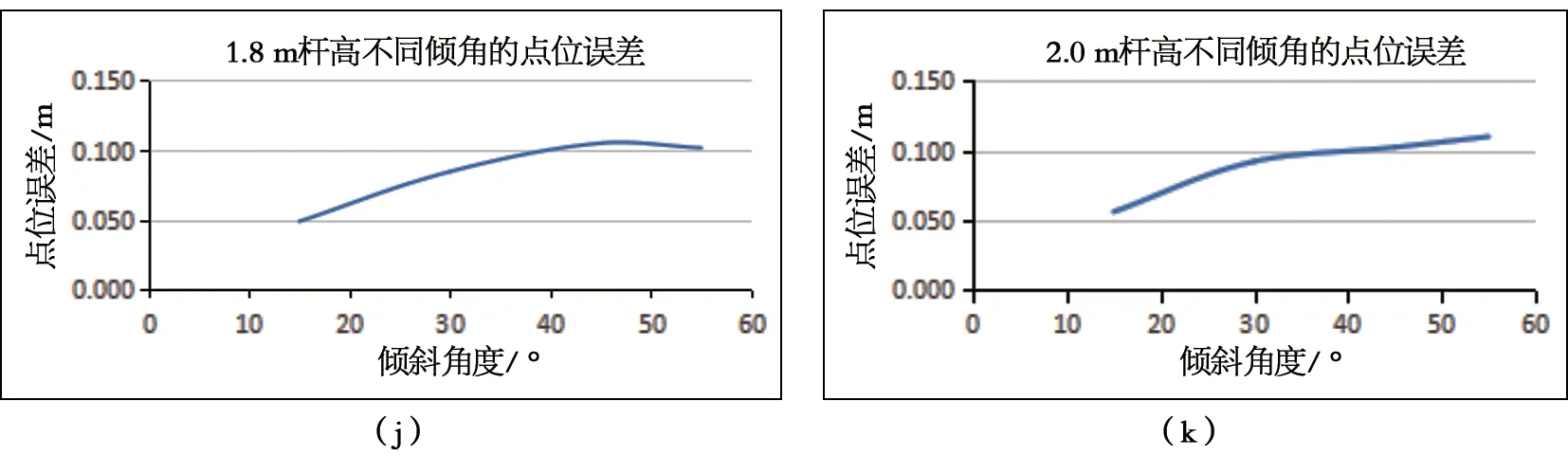
图4 倾斜角度与点位误差关系图
根据图4可以看出倾斜方向相同、杆高相同条件下,倾斜角度对测点精度的影响表现出基本相似的特征,即惯导RTK倾斜测量时对中杆的倾斜角度对点位精度的影响具有一定的规律性,在倾斜角度在40°左右时,点位误差曲线会出现一次斜率变化,充分验证了惯导RTK倾斜偏距与平面点位精度的相关关系。
4 倾斜测量对高程精度影响分析
根据前面实验数据分析得知,倾斜测量时杆高、倾斜角度、倾斜方向均对平面点位精度有一定的影响,而由公式(2)可知,倾斜测量的高程影响因素主要为杆高和倾斜角度,而这两种因素共同影响结果为偏距的变化,其数值精度取决于加速度计对倾斜角度测定的准确性,所以根据表1实验数据,以偏距为横轴,高差为纵轴绘制折线关系图如图5所示。

图5 偏距对高差的影响图
从图5可以看出高差随着偏距的增大而增大,R2为0.907,基本符合线性特征,当偏距为 0.9 m左右时,高差大致为 5 cm,与偏距对平面点位精度影响程度相比要小,因此可知,倾斜测量对高程精度的影响不大。
5 结 论
根据对惯导RTK倾斜测量的实测数据分析得到以下结论:
(1)惯导RTK在进行倾斜测量时测点精度主要受倾斜偏距的影响,且偏距对平面点位精度和对高程的影响均基本符合线性特征,随着偏距的增大,点位精度逐渐降低,实际测量中无论是杆高的变化还是倾斜角度的变化,整体上应控制倾斜偏距在 46.6 cm以内,才能将测点精度控制在 5 cm之内,如果偏距过大超过 1.8 m,则点位精度将增大至 10 cm,这将直接影响倾斜测量的可靠性,因此应该严格控制偏距来控制测点精度。
(2)倾斜方向对倾斜测量结果也具有一定程度的影响,根据实验表明,惯导RTK在进行倾斜测量时倾斜正北或正南方向时,点位精度的变化具有一定的规律性,而偏向正东方向时表现出震荡的特征,且无明显变化规律,精度不可控性较大,因此在实际工作中,应该尽可能控制倾斜方向为正北或正南方向。
(3)惯导RTK倾斜测量时倾斜偏距对高程的影响也基本符合线性特征,但对平面点位精度的影响明显要大于对高程的影响。
