The First Photometric Study of W UMa Binary System V1833 Ori

Mehmet Tanrıver and Ahmet Bulut

1 Astronomy and Space Science,Science Faculty,University of Erciyes,TR-38039,Kayseri,Türkiye; mtanriver@erciyes.edu.tr

2 Erciyes University,Astronomy and Space Science Observatory Application and Research Center,TR-38039,Kayseri,Türkiye

3 Department of Physics,Faculty of Arts and Sciences,Çanakkale Onsekiz Mart University,Terzioglu Campus,TR-17020,Çanakkale,Türkiye

4 Astrophysics Research Center and Observatory,Çanakkale Onsekiz Mart University,Terzioglu Campus,TR-17020,Çanakkale,Türkiye

Abstract The first photometric solution in the B,V,Rc and Ic filters of the short period V1833 Ori eclipsing binary is presented based on new ground-based CCD photometric observations.We analyzed the BVRI photometric light curves of the system,using PHOEBE 0.31a,a binary star modeling program,with the Wilson-Devinney method based on Roche geometry to achieve the best accordance with the photometric observations to determine their absolute parameters from the light curves.We updated the ephemeris of V1833 Ori using two new light curve minima derived by our new observational data from those collected in the literature and analyzed the change of the system’s orbital period.The O–C analysis indicates that the variations of the orbital period of V1833 Ori with time are increasing at a rate of 3.03×10−7 days yr−1.The distance of V1833 Ori is 173.7±15.6 pc.From the solutions,we find that V1833 Ori is an A-subtype W UMa overcontact binary with q=0.701 mass ratio and f=1.14 fill-out factor.The HR diagram positions of the eclipsing binary system’s components are discussed.The system’s absolute dimensions were compared to those of similar binaries in the log Teff-log L,logM−logL,logM−logR and log M-log J0diagrams.

Key words: (stars:) binaries: eclipsing–stars: fundamental parameters–stars: individual (V1833 Ori)

1.Introduction

V1833 Ori (TYC 684-1316-1) is classified as a W UMa type eclipsing binary star.W UMa type binaries comprise two contact cool components surrounded by a convective envelope located in the region between the first(inner)and next(outer)critical Roche surfaces/boundaries (Mochnacki1981).Low mass contact binaries (LMCBs) are the W UMa type variables that have periods and total mass less than 0.d3 and 1.4M⊙respectively.The more massive components of LMCBs have generally lower temperature than the other companion stars and are grouped as W-subtype variables by Binnendijk (1970).Despite different component masses,they possess almost identical surface brightnesses.The high mass component stars of these W UMa-type systems are typically a main sequence(MS) star located close to the zero age main sequence (ZAMS) whereas the lower mass component exceeds,sometimes by a factor of several,its expected ZAMS radius (Stȩpień2006).

We analyze the light curves of the contact W UMa system,V1833 Ori,to determine the absolute parameters of the contact binaries in this study.We obtain CCD observations with multibands from the 30 cm telescope in Çanakkale Ulupınar Observatory (UPO) in Turkey and optimally create binary star models suitable for these observations using the Wilson-Devinney(WD) based PHOEBE 0.31a interface program (Wilson &Devinney1971;Wilson1979;Prša&Zwitter2005).The present study is the first in-depth photometric analysis of this system.Otero et al.(2004) presented new eclipsing binaries found in the Northern Sky Variability Survey(NSVS)database.GSC 00 684-01316(SAO 112 139)is among them.Kazarovets et al.(2011),in the 80th name list of variable stars,listed GSC 00 684-01316(SAO 112 139) with the name V1833 Ori.Nelson (2016)presented CCD minima for the selected eclipsing binaries in 2015 including V1833 Ori.Huber et al.(2016)presented the K2 Ecliptic Plane Input Catalog (EPIC) and stellar classifications of 138,600 targets,which included V1833 Ori.We perform the first analysis of the photometric data received as observational.We obtain the new stellar parameters of the binary system from the light curve solutions and get the absolute values of the masses and radii of the component stars.

The following sections present observations,image reduction and instruments used,light curve analysis,the result of photometry,ephemerides and period analysis,light curve behavior,spectral classification,absolute parameters,mass change and finally,the conclusions and discussion.The binary system’s infrared magnitudes and color indices are available in the 2MASS catalog.In the Tycho-2 catalog,V1833 Ori’sVmagnitude is reported as 10.548 mag.General information on these stars is provided in Table1.

2.Observations and Image Reduction

2.1.Photometric Observations

The photometric instrument included a 30 cm Schmidt-Cassegrain telescope equipped with BesselBVRIfilters+theApogee Alta U47 CCD camera at UPO in Çanakkale Onsekiz Mart University in Turkey.We performed automated imaging with the BessellB,V,RcandIcfilters.For the V1833 Ori system,we obtained 566,544,566 and 526 CCD image frames in theB,V,RcandIcfilters,respectively.Exposure times for all image frames in theB,V,RcandIcfilters were adjusted to 60 s,50 s,40 s and 30 s,respectively.We performed image acquisition (i.e.,bias,dark and flat) using ccdsoft.v5 software while we executed calibration and recording with aip4win v2.4.0 (Berry &Burnell2005).We accomplished further photometric reduction on the light curves of V1833 Ori using the comparison and check stars that showed no change in magnitude,as given in Table1for the same field.We minimized errors from differential refraction and color extinction since we only took data image frames above 30°altitude (i.e.,air mass <2.0).

Table 1The General Information on V1833 Ori,Comparison and Check Stars

2.2.Light Curve Analysis

We performed light curve analysis of the V1833 Ori binary system with the PHOEBE 0.31a program(Prša&Zwitter2005)based on the WD binary star model(Wilson&Devinney1971;Wilson1979).The Roche geometries of the binary stars were generated by Binary Maker 3 (BM3) (Bradstreet &Steelman2002) after the model fitting was completed.We used Nelson(2013)’s freeware interactive program,including the method of Kwee &van Woerden (1956),to calculate new minimum times of the binaries as displayed in Table2.The minimum times in the earlier study and in this study were used to get the potential orbital period changing using mid-eclipse times.For this,Transiting Exoplanet Survey Satellite (TESS) and All Sky Automated Survey (ASAS) studies were also taken into account.

3.Results

3.1.Photometry,Ephemerides and Period Analysis

The comparison and check stars of V1833 Ori in the same image frame (field of view: FOV) were noted to show no photometric variation with the equipment used for this study.During image acquisition,scattering of the observation points of the V1833 Ori system manifested in a change of±0.018 mag,±0.019 mag,±0.013 mag and±0.015 mag for theB,V,RcandIcbands,respectively.Photometric values inB,V,RcandIcfor V1833 Ori were processed to generate four light curves that spanned 6 days between 2020 October 10 and November 20.In total,a new primary minimum (MinI) and a secondary (MinII)minimum were obtained separately for both stars during this study.Since we recorded no color dependence on the timings,we averaged data acquired from all filters.

A new linear ephemeris for the mid-eclipse timings obtained from this study and collected from the literature was appointed with the following light elements (Equation1).

This study provided the first analysis of orbital period changes for the V1833 Ori binary system;693 eclipse timings for V1833 Ori,including this work,are listed in Table2.These minimum times of the binary system were used to calculate the revised orbital period,as shown in Equation(2).We found the revised period to be 0d.37720104 for V1833 Ori.

Table 2The Observed BJD Minima Minus Calculated Minima (O−C) values of V1833 Ori

We used the least-squares method to generate the (O–C)residuals,as expressed in Equation(3).The(O–C)curves yield an upward quadratic polynomial,as displayed in Figure1.We can interpret this as the increase of the orbital period at a rate ofdP/dt=3.03×10−7d yr−1for V1833 Ori.

The change of orbital period in binary star systems is explained by some different mechanisms as conserved mass transfer or non-conservative mass loss,magnetic activity,the effect of a third body in the binary system or apsidal motion.Determining the reason for the period change of a system is based on the interpretation of the change ofO-Cdifference according to time.O-Canalyses of binary stars are generally complex.These commonly comprise some cyclical changes superimposed in an upward or downward parabolic change.Parabolic variations are generally explained by mass transfer and mass loss with conservative or non-conservative angular momentum.Although the sinus-like variations are generally accepted to be caused by a possible third body revolving around the binary system,as alternatives,they can also be explained with magnetic cycles of cool and active stars in the binary system (Applegate1992).Applegate (1992) proposed a model based on magnetic activity which describes such cyclicchanges and deduced that variations in the active star have to be at the ΔLRMS/L≈0.1 level.

3.2.Light Curve Behavior

The secondary minimum of V1833 Ori in Figure2implies that the system is undergoing a partial eclipse when the hotter and larger component covers the cooler and smaller component.In the light curve,the maximum light level defined as secondary maximum (Maximum II-MaxII) around phase 0.75 is lower than the maximum light level defined as primary maximum(Maximum I-MaxI) around phase 0.25.This is the positive state of the O’Connell effect,which is ascertained from especially remarkable photometric observations of V1833 Ori collected during 2020 as shown in Figure2.The asymmetry,where the maximum levels are unequal,has usually been attributed to a stellar spot,impact effect from a gas stream and/or other stellar surface disturbances(Yakut&Eggleton2005).Unequal heights during maximum light of the system can be simulated by adding starspot(s) to the star surface during the analysis using the light curve data for Roche modeling.

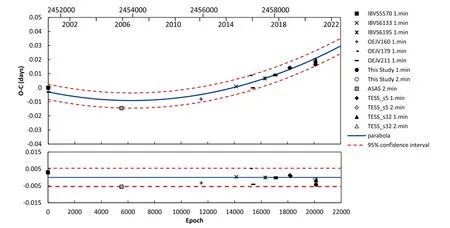
Figure 1.The O-C diagram of the V1833 Ori system.The blue solid line represents the parabolic fitting curve.The dashed red lines signify the 95% confidence interval.The residuals are shown at the bottom of the panel.

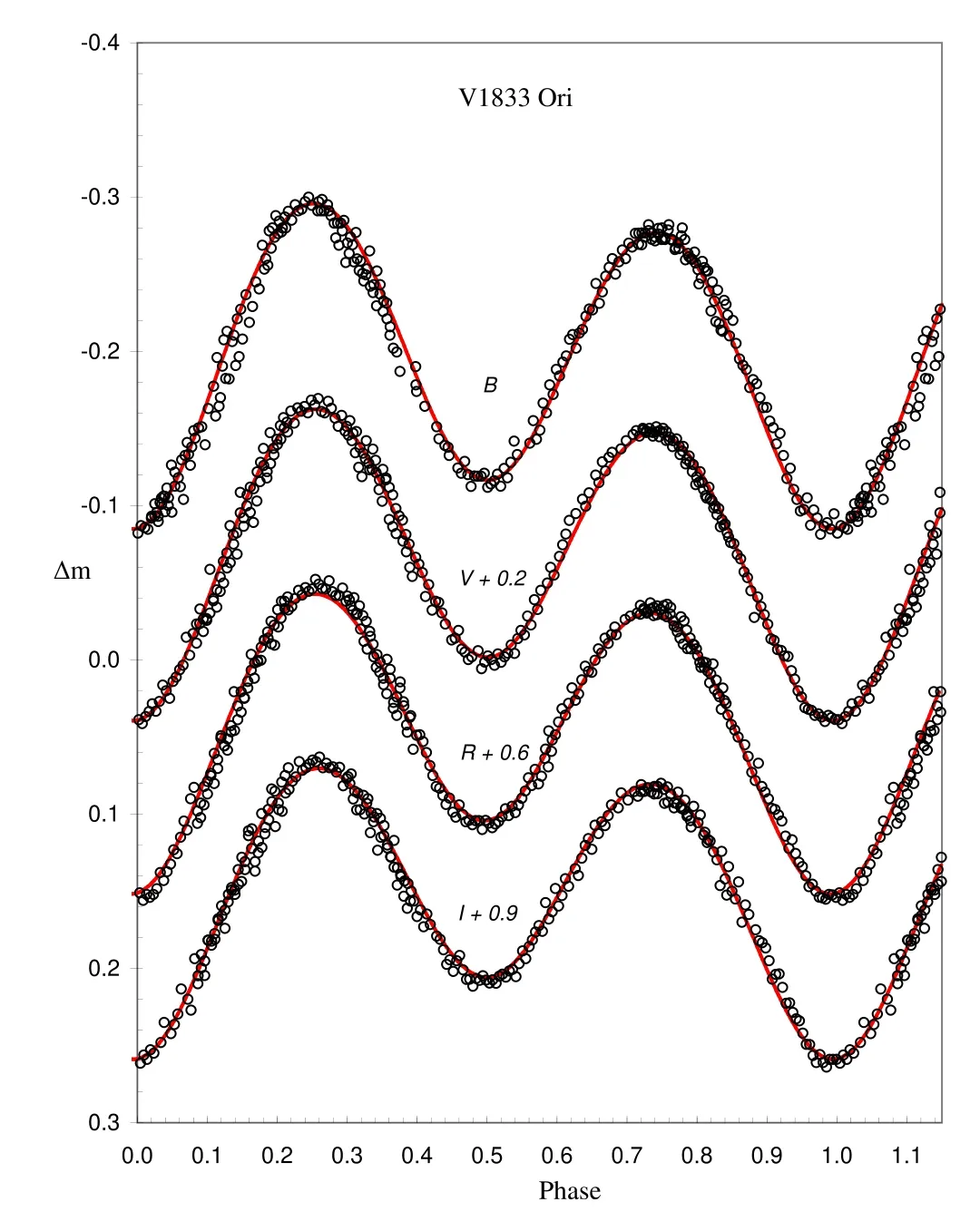
Figure 2.Synthetic fits (solid-red line) of V1833 Ori light curves,with the hotter spot in B, V, Rc and Ic.

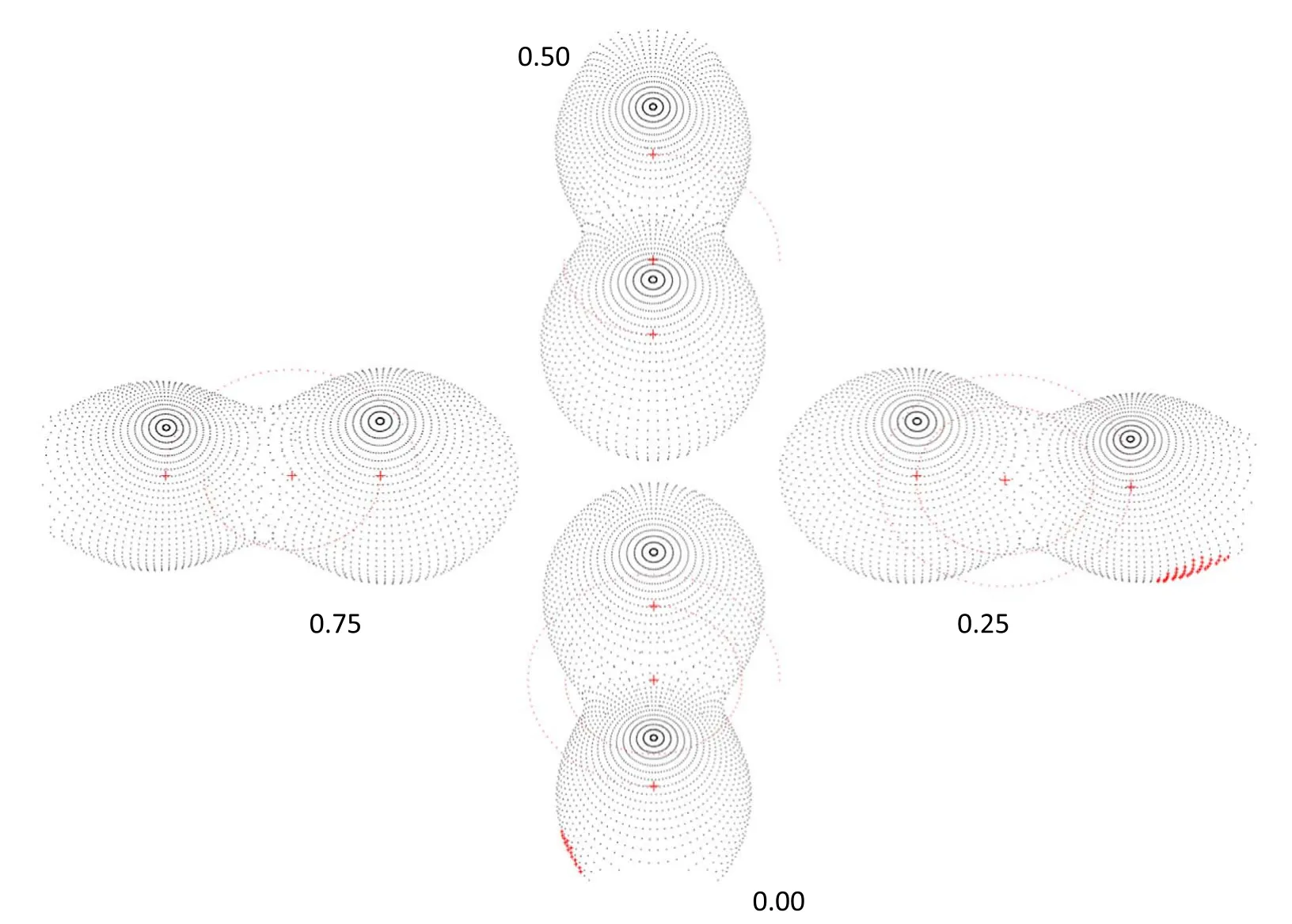
Figure 3.The Roche geometries of V1833 Ori binary system according to the orbital phases 0.00,0.25,0.50 and 0.75.

3.3.Spectral Classification

Table3lists the (J–H)0color index data from the other catalogs or surveys corrected using theAHinterstellar extinction(i.e.,E(J−H)=0.022 mag,AH=0.288 mag,for V1833 Ori usingAVSFD= 0.3353(NASA/IPAC),AH/E(J−H)=1.42(Nishiyama et al.2006) andAH/AV=0.108 (Nishiyama et al.2008)derived for targets in the Galaxy according to the algorithm given by Schlafly&Finkbeiner(2011).Distance of 173.7 pc was acquired from extinction calculations to be used for V1833 Ori.The mean result (J−H)0=0.324±0.055 mag for V1833 Ori,utilized for later Roche modeling,indicated that the massive,hotter and larger star in the system had aTeffeffective temperature of 5331Kfor V1833 Ori.It also ranged in spectral type between G4V and G6V for V1833 Ori (Pecaut &Mamajek2013).Throughout this article,regardless of its effective temperature,we consider the more massive star to be the primary and denote it with the subscript “1”,and “2” designates the secondary,smaller star.

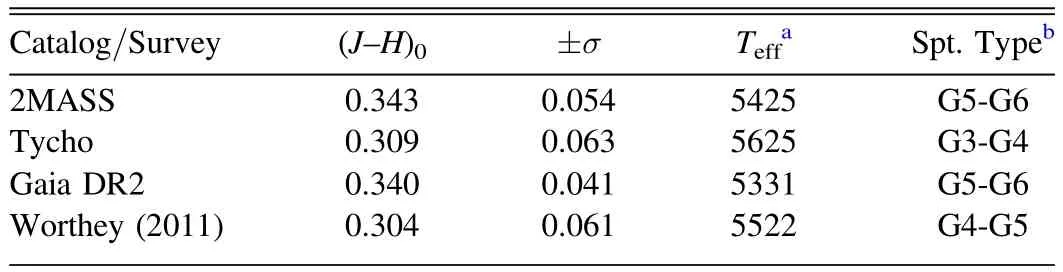
Table 3Spectral Classifications of V1833 Ori Based On Different Catalogs

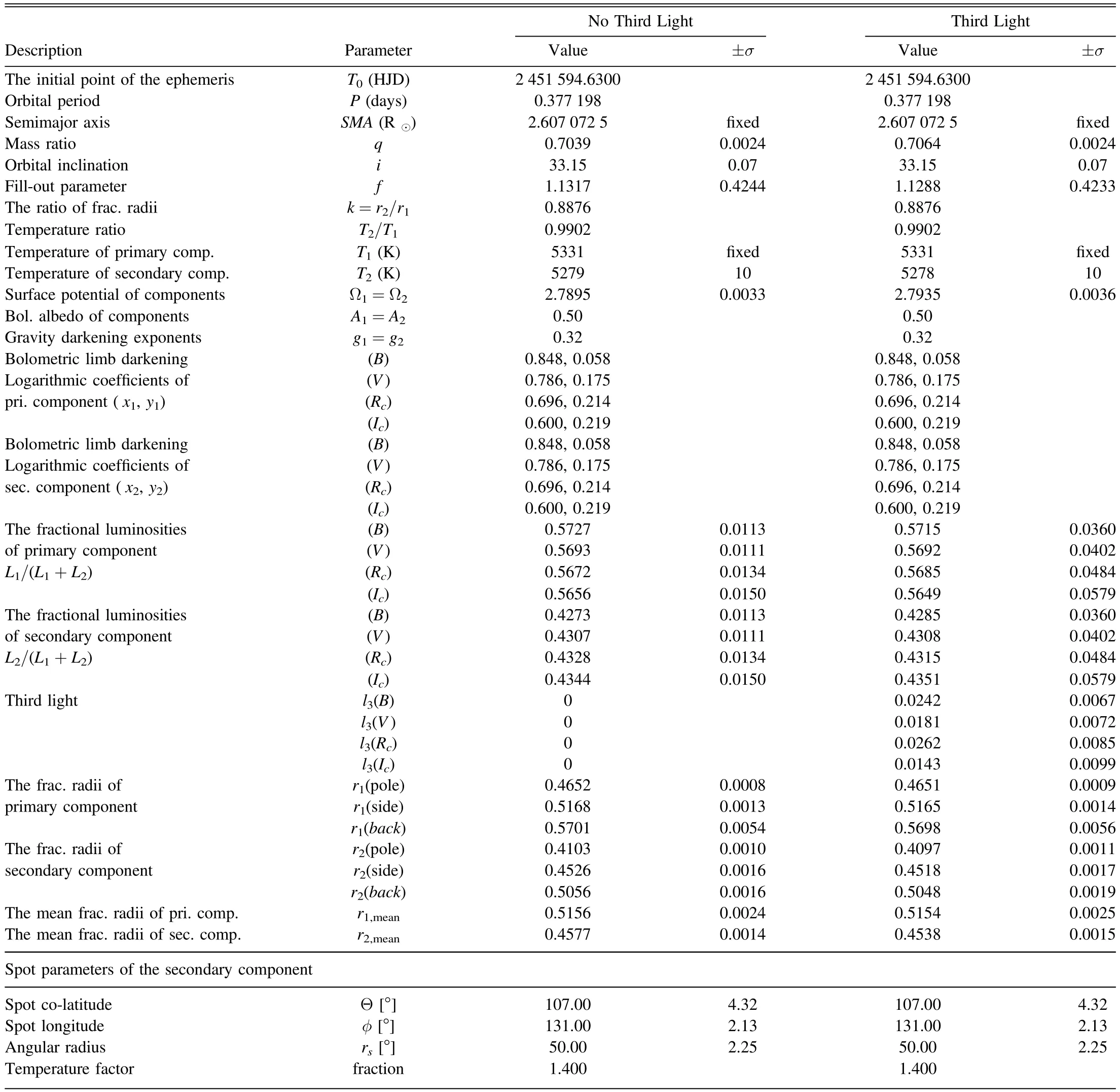
Table 4The Solution Parameters of V1833 Ori with Hot Spot

3.4.Roche Modeling

The lack of radial velocity (RV) data makes it difficult to establish precisely theqmass ratio or whether the binary system is an A-subtype or W-subtype W UMa binary system.Binary systems with late spectral types and short orbital periods are normally related to W-subtype.However,the deepest minimum (i.e.,primary min.-MinI) of the light curves should occur when the smaller and cooler component of the binary system occults the larger and hotter component in the system.Conversely,the light curve indicates a partial eclipse of the secondary star occurring at the secondary minimum-MinII,while the primary minimum-MinI originates from the transition through the primary star.We progressed with WD modeling under the assumption that this system is a W UMa binary star.Roche modeling of the light curve data for V1833 Ori was mainly realized using the PHOEBE 0.31a interface program(Prša &Zwitter2005).We selected a model for an “overcontact binary not in thermal contact” (Mode=3).The bolometric albedoA1,2=0.5 and the gravity darkening coefficientg1,2=0.32 for the cooler star with temperature<7200Kwere determined according to Ruciński (1969) and Lucy(1967).The effective temperature of the massive primary star in the V1833 Ori binary system was fixed atT1=5881 K.Any changes in the secondary component’s effective temperatureT2prompted the interpolation of new bolometric limbdarkening logarithmic coefficients(x1,y1,x2,y2)in accordance with van Hamme (1993).We allowed all parameters to vary apart fromT1,A1,2andg1,2during the solution iterations of the light curves.

It is necessary for the secondary star in an A-subtype to have a lower effective temperature compared to the primary star to obtain the most suitable light curve simulations.This solution only includes the analysis of light curves for V1833 Ori by adding a stellar spot to the star surface,since the maximum levels in the related photometric light curves are not equal,showing the O’Connell effect.

3.5.Analysis of the Light Curve

The first evaluations forT2,iandqquickly converged to the best Roche model fit,as shown in Table4.5Errors in Tables 3–4 are obtained from the light curve solution.The simulations of spotted solutions for V1833 Ori in Figure2revealed that,according to expectations for A-subtype W UMa eclipsing binaries,the effective temperature of the secondary star with less mass is lower and cooler than the primary star.

A Roche surface outline model created with BM3(Bradstreet&Steelman2002) using the solution and astrophysical absolute parameters from the photometric light curves is displayed in Figures3and4.After we found the best model agreement and solutions,we investigated the values and errors forT2,Ω1,2,iandqas detailed using PHOEBE,where we executed the WD minimization program 500 times,repeatedly (Prša &Zwitter2005).During each scan,we automatically updated input parameters to actualize the next iterations.Thereafter,we obtained,from the standard deviation observed with the resulting parameters,the formal errors for the fundamental parameters of the binary system.Binary systems that do not show a total eclipse are affected by degenerate results,wheni-inclination andq-mass ratio are simultaneously varying during WD modeling.Thus,a dependable determination ofq,the mass ratio,is impossible (Terrell &Wilson2005).There is no total eclipse at either MinI or MinII in the light curves of V1833 Ori,and only partial eclipses are seen.

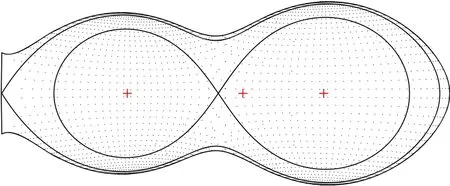
Figure 4.The Roche surface outline configuration of the V1833 Ori binary system.

Since the spectroscopic RV data were not available for the binary system investigated in this study,we determinedqusing the comprehensiveq-search method from the modeling of the light curve to determine the most likely mass ratio.With this technique,we calculated the q test results at a series ofq-mass ratios,with the values ranging from 0.10 to 1.0 in steps of 0.01.We obtained a fit solution for every assumedqvalue and plotted the sum of squared deviations corresponding to everyqvalue.We identified theqvalues corresponding to the minima of the squared deviations’sum for the system as the initial mass ratios in the modeling.The diagram in Figure5affirms that,for V1833 Ori,a minimum occurs at a value aroundq=0.70.

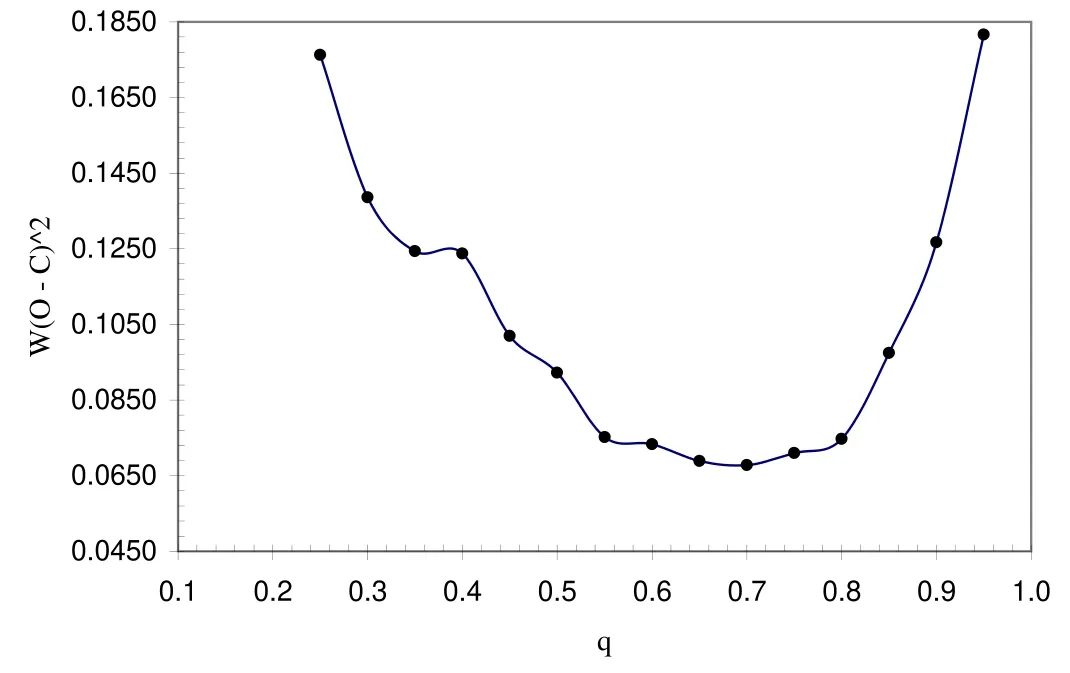
Figure 5.The q-search diagram of the V1833 Ori binary system.

However,we should emphasize that the given errors arise exclusively from fitting the model to the observations,thus accepting accurate values for all unchanging parameters.TheT1uncertainty relative to (B–V)0is,in particular,not much lower than ∼200–300 K if we consider photometric and calibration errors,the calculation ofE(B–V),etc.

LMCB stars are typically active with low temperatures,late spectral type (G-K) and magnetic activity (Stȩpień &Gazeas2012).Considering these situations,we can cover a part of the star’s surface with spot(s).Our study reveals a positive O’Connell effect,where the MaxI level is slightly higher than the MaxII level(MaxI>MaxII),for V1833 Ori as shown in Figure2.It is normally unclear whether this effect originates from a decrease during phases 0.25 and 0.75 from the cool spot on either component looking at the observer,or an increase caused by a hot spot during maximum brightness.As specified by Kallrath &Milone (1999),“color amplitudes increase when going to V→R→I as expected for cool spots”.The opposite of this is valid for a hot spot.According to the photometric studies of the V1833 Ori binary system,the color amplitudes show a decrease,lending credence to the existence of a hot spot.For V1833 Ori,we see that there is some discrepancy in the light curves.To address this,we placed a spot on one component of the system and assumed a spot is on the secondary component.We applied a second-order polynomial regression to the sample data of Berdyugina (2005) to determine the spot’s temperature factor.Equation (4) below presents the polynomial fit.

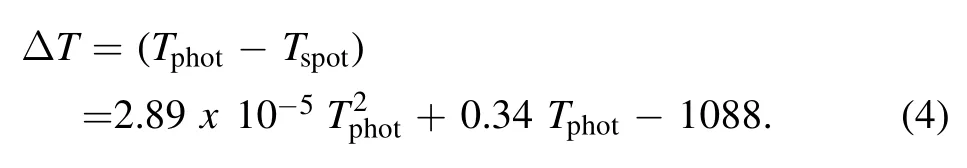
TspotandTphotare spot and photosphere temperatures,respectively.For the hot spots,the temperature factor is greater than 1.Several groups of them are tested.Finally,a converged solution was found with a hot spot on the secondary component of the V1833 Ori system.The solution parameters for the V1833 Ori system are listed in Table4.

We provided initial fits with the parameters ofi,q,T2and Ω1,2from the 2020 light curves.All other parameters (i.e.,A1,2,g1,2andT1) remained fixed during the differential correction (DC) process.We added a hot spot into the modeling to simulate asymmetry at the maximum level of the light curve.We summarized the related geometric and astrophysical elements of the V1833 Ori binary system in Table4,the Roche geometries in Figures3and4,and the observational and synthetic light curves in Figure2.A hotter spot placed on the secondary star produced the most suitable light curve for V1833 Ori.All curves presented in this study represent a look into the behavior of V1833 Ori,which also shows differences from the Roche modeling.

3.6.Absolute Parameters

We calculated absolute parameters shown in Table5for every A-subtype W UMa binary system using consequences for the most suitable model of the 2020 light curves.Total mass cannot be computed directly without RV data.However,in the literature,the masses,radii and luminosity values of binary stars are given in tables.Some statistical relations between absolute parameters were used to calculate the absolute parameters.A recent example was provided by Gazeas &Stȩpień(2008).Using both W-subtype and A-subtype W UMa samples they presented,we derived a logarithmic relation between the semimajor axis—aand the period—Pin Equation (5).The correlation coefficient isR2=0.95,and Figure6yields more information.

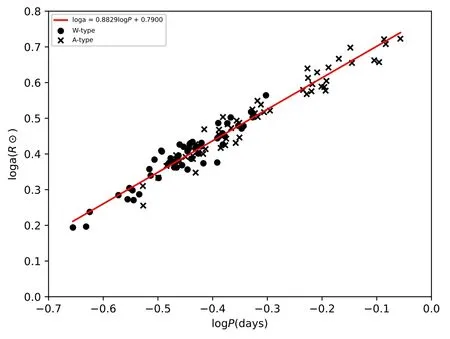
Figure 6.The logP—loga relation obtained from the W UMa samples of Gazeas &Stȩpień (2008).

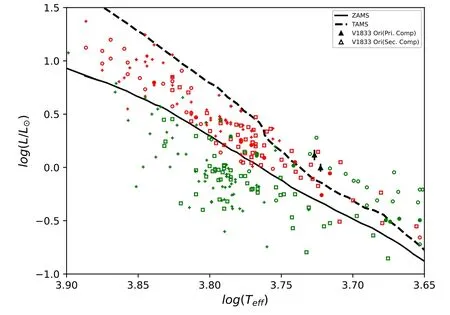
Figure 7.The positions of V1833 Ori on the HR diagram with the ZAMS and TAMS lines of Girardi et al.(2000) [Z=0.02 (solar)].The primary and secondary stars of V1833 Ori are black filled and empty diamonds respectively.The W-subtype contact binaries,A-subtype contact binaries,near contact binaries and detached binaries of the sample systems obtained from Yakut &Eggleton (2005) are represented by “☐”,“+”,“◦”,and “•”,respectively.The primary stars of every type are red,and the secondary stars are green.Error in temperature remains within the symbol.

Pandaare in units of days andR⊙,respectively.Since the binary system does not have RV data,we defined its orbit’s semimajor axis using this relationship.The semimajor axis of the V1833 Ori eclipsing binary system wasa[R⊙]=2.607±0.101.

Theqmass ratio of the V1833 Ori eclipsing binary system was 0.7039±0.0024.Using the semimajor axis-a(R⊙) values and the obtainedqmass ratios together with Kepler’s corrected third law,M1(1+q)=a3/P2andq=M2/M1,we computed the mass of the primary star for the V1833 Ori binary system,which turned out to beM1=0.982±0.115M⊙.Then,using the derived semimajor axis (a[R⊙]) values together with the fractional radii(r1,2),we computed the radii of each component star in the unit of solar radius from the expressionr1,2=R1,2/a.The resultant values of our computations for the absolute parameters using Equation (5) are presented in Table5.The V1833 Ori system’s other absolute parameters using thephotometric elements areM2=0.691±0.082M⊙,R1=1.344±0.058R⊙,andR2=1.193±0.035R⊙.

Table 5The Absolute Parameters of V1833 Ori

The fill-out parameter(f),an indication of the contact degree between companion stars of the binary system,was calculated using the expression (Ωin–Ω)/(Ωin—Ωo) (Lucy &Wilson1979),where Ωorepresents the outer Roche equipotential (the outer critical Lagrangian potentials),Ωinthe equipotential value for the inner critical Roche surface and Ω=Ω1,2demonstrates the surface potentials for the companion stars of the binary system and varied from 0 to 1 from the inner critical surface to the outer critical Roche surface.We defined the system as a“contact binary” since the calculated fill-out value of V1833 Ori wasf=1.1317.

We computed the luminosities of the companion stars and the bolometric absolute magnitude of the binary system from the bolometric absolute magnitudes (Mbol1== 4m.75) obtained from the PHOEBE solution using the well-known astrophysical standard relationship of Equation (6) below.

The suffix ⋆refers to either component of the system andMbol,⊙=4.74 mag (Cox2000).The bolometric absolute magnitude of the system isMbol,system=3.83 mag.Thelogg()values of V1833 Ori are compatible with the values determined using the masses and radii of the primary and secondary components within an error range (l og (g1) =4.17,log(g2)=4.12).The mean densities of the binary system were obtained using Mochnacki (1981)’s equations.The mean densities of V1833 Ori’s components were ρ1=0.57±0.02 and ρ2=0.57±0.02.

We used Schlafly &Finkbeiner (2011)’s reddening maps and the interstellar extinction calculator(Av)in NASA/IPAC’s Extragalactic Database (Helou1990).UsingMbol(system)=3m.83 and BC=−0.18 in the V1833 Ori binary system,assuming that they are MS stars and taking into account interstellar extinction,Av=0.335,we determined the distance of the system to be 173.7±15.6 pc when employing Equation(7).The parallax of V1833 Ori is given as 6.2542±0.0154 mas in the Gaia EDR3 catalog.The Gaia distance of the system is 159.9±0.4 pc.This value is in agreement with our resulting distance.

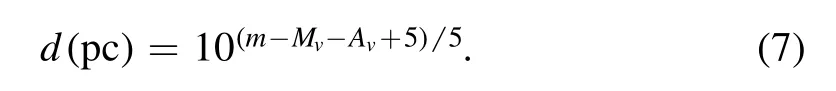
We showed the position of the system composing our target,together with other W UMa type binaries,on thelogTeff-logL(Hertzsprung-Russell: HR diagram),logM−logR,logM−logL,logM-logJ0and logTeff-logLdiagrams with corresponding evolutionary tracks in Figures7–11.

4.Conclusions and Discussion

This study utilized comprehensive and iterative modeling using the PHOEBE 0.31a interface program based on the WD method to obtain valuable information regarding an eclipsing binary system.The light curve analysis of the V1833 Ori binary system made it possible for us to calculate its components’fundamental parameters.The results revealed the system’s overcontact configuration,and thus how the secondary component (i.e.,smaller star) and the primary component(i.e.,larger star)filled their Roche lobes.These results suggested probable mutual mass exchange between the components.

The absolute astrophysical parameters of the system’s components were obtained based on the results of the light curve calculation.The results indicate that V1833 Ori is a deep contact binary according to the criteria stated by Qian et al.(2005).The fill-out parameter of V1833 Ori isf>1,which would therefore make it evolve and lose its outer envelope on a dynamical timescale.This situation can be seen in Figure7.Both components of V1833 Ori are outside the terminal age main sequence (TAMS) line.The system’s photometric mass ratio suggested that they are low-temperature contact binary(LTCB) systems.de Jager &Nieuwenhuijzen (1987)’s tables demonstrated that the spectral types of V1833 Ori’s components were G8.

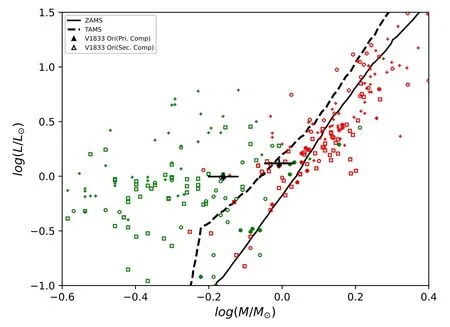
Figure 8.The positions of V1833 Ori on the logM–logL plot.The symbols,the sample systems,and the ZAMS and TAMS lines are the same as in Figure 7.

Figure 9.The positions of V1833 Ori on the logM−logR plot.The symbols,the sample systems,and the ZAMS and TAMS lines are the same as in Figure 7.

Figure 10.The positions of V1833 Ori on the logM–l ogJ0 plot under the Jlim borderline separating detached and contact binaries as reported by Eker et al.(2006).The symbols are the same as those defined in Figures 1 and 4 in the original article by Eker et al.(2006).The crosses represent the A-subtype W UMa systems,and the circles signify the W-subtype W UMa systems.Error in logJ0 remains within the symbols.

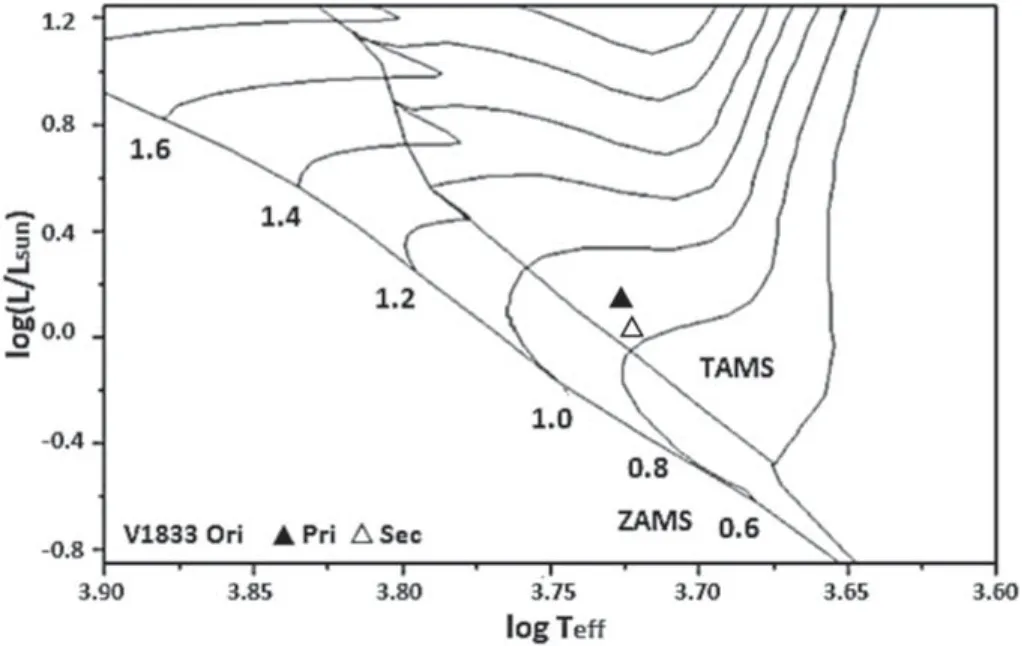
Figure 11.The components of V1833 Ori(triangles)plotted in the HR diagram with ZAMS,TAMS,evolutionary tracks and isochrones obtained from Girardi et al.(2000) for the chemical composition of the Sun [Z=0.02].Errors in temperature and luminosity remain within the symbols.

The contact W UMa type systems containing two MS stars with late spectral type commonly display asymmetries in their light curves.Binnendijk (1960) demonstrated the asymmetries result from hot or cool spots on one or two stars because of magnetic activity.Thereafter,Binnendijk(1965,1970)divided W UMa systems into A-type and W-type subclasses,where the primary minimum-MinI respectively takes place as occultation and transit.The morphologies of the binary system’s light curves show that the system is an A-subtype W UMa binary.A-subtype systems feature a larger star transiting in the deeper minimum,evolve more than W-subtype and their MinI occurs when the hotter and larger component is occulted by the cooler and less massive component.Therefore,we state that the binary system in this study is of the A-subtype W UMa variable star.TheO-Ccurve indicates that the orbital period of V1833 Ori binary system is increasing.

Some W UMa type binary systems showing increasing orbital period variation were compared with thedP/dtvalue of the V1833 Ori binary system,and these were listed in Table6.The period increasing rate for V1833 Ori was found to be a compatible typical value according to other W UMa type binary systems.

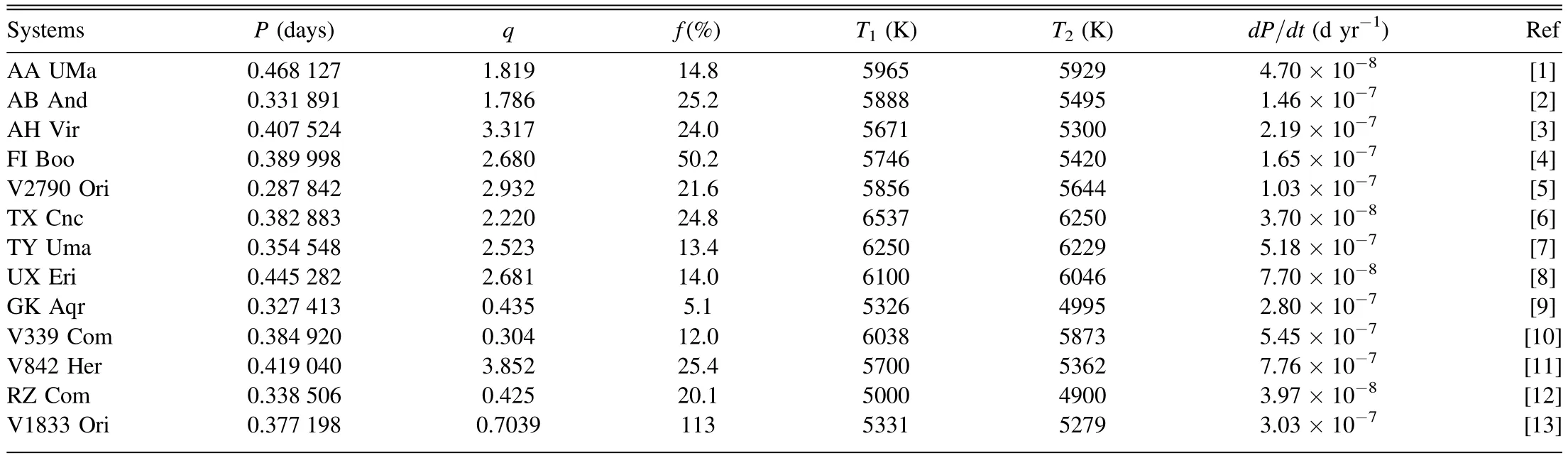
Table 6Some W UMa Type Binary Systems with Increasing Orbital Period Variation

Using the angular momentum equation of Eker et al.(2006),the angular momentumlogJ0value of V1833 Ori calculated according to the absolute parameters obtained in this study are 51.709,andlogJlimvalue is 51.713.ThislogJ0value is less than thelogJlimvalue (logJ0< logJlim).According to our solution parameters,this indicates that V1833 Ori is in the contact zone of the logM–logJ0plot in Eker et al.(2006)’s study as further shown in Figure10.

Considering the system’s fundamental characteristics,such as the mass ratio,orbital period and hotter primary component,V1833 Ori is compatible with other types of contact binaries(Yakut &Eggleton2005;Eker et al.2006).Based on the eclipsing binary system’s computed absolute parameters,we compared the components’ positions of the V1833 Ori with W-subtype LTCB,A-subtype LTCB,NCB and DCB samples using plots such as logM-logL,logM-logR,logM-logJ0and logTeff-logLprovided by Girardi et al.(2000) as displayed in Figures7–11.We also calculated the V1833 Ori binary system’s evolutionary status using evolutionary tracks and isochrones.

We plotted V1833 Ori’s components and selected binary systems as the mass-luminosity,mass-radius,effective temperature-luminosity (HR diagrams and evolutionary tracks) and mass-orbital angular momentum in Figures7–11.We demonstrated that the binary system’s components agreed with their analogs.V1833 Ori also agreed with the evolutionary tracks of 0.9M⊙,a single star with a solar chemical composition considering their primary components’ absolute parameters.The locations of the V1833 Ori’s primary and secondary star in the HR diagram are appropriate for masses of a binary system by comparing with stellar evolutionary models.As demonstrated by the figures,the primary and secondary components of V1833 Ori system were located outside of the TAMS(Figures7and9).The primary component was located between the ZAMS and TAMS according to Figure8.These results indicated that the primary and secondary components of the system were evolved stars.It is possible that the system’s components were losing their masses and exchanged with each other.There is a mass transfer from the secondary(less massive)to the primary (more massive) star (see Figure1).The components’locations of V1833 Ori on the logM/M⊙—logL/L⊙and logM/M⊙—logR/R⊙diagrams confirm that the secondary has evolved to be less-luminous and less-sized,while the primary is still an MS star.

According to the obtained binary system’s solution parameters,we produced Roche configurations of the member starsof the binary system using the Binary Maker 3.0 program(Bradstreet &Steelman2002) as depicted in Figures3–4.

V1833 Ori possibly evolved from a contact binary star into a single with rapidly rotating stars like other low mass ratio contact systems.However,the existing observations are unsatisfactory for identifying any periodic changes that could explain the decrease in the mass ratio of the binary system.The binary system’s evolution is strongly affected by the presence of a companion star.Components with smaller masses have photometric properties that are strongly affected by the presence of companion stars,and their position on the HR diagram may be far from the position of an MS star with the same mass.The internal constitution may also be very different(some researchers assume that it is still on the MS,whereas others argue that less massive components strongly evolve with a helium core).The primary component of V1833 Ori is close to the MS due to the system’s small mass ratio.

We calculated the distance of the V1833 Ori binary system asd=173.7±15.6 pc according to the estimated absolute parameters.This distance is compatible with the distance value(d=159.9 pc) obtained from the parallax of the Gaia EDR3.

In summary,V1833 Ori is a very interesting binary star that appears to be an overcontact binary star.This eclipsing binary system’s component stars have overfilled Roche lobes.The primary star is the more massive component.The secondary component is the less massive star.A comparison with the W UMa stars from the literature shows that the obtained absolute parameters of the binary system are roundly within expected ranges.However,without spectroscopic studies,which are required for an entirely confident determination of spectral types,the mass ratio,semimajor axis and absolute stellar parameters of our system in this study should be regarded as preliminary values.To validate the current results and to reveal the true nature of this system,making a combined more precise spectroscopic and photometric observation of these binary stars would be significant for understanding this contact binary.Using imaging techniques to confirm the existence and determine the positions of stellar spots would make useful contributions to our knowledge about this system,and we invite researchers to undertake the necessary spectroscopic and photometric observations.

Acknowledgments

This study was supported by the Scientific Research Projects Coordination Unit of Erciyes University(project number FBA–09–788).We thank Çanakkale Onsekiz Mart University Ulupınar Observatory (ÇOMU–UPO) for support in allowing use of their T30 telescope.We gratefully acknowledge the SIMBAD,ADS,CRTS,TESS,BRNO O-C Gateway,Kraków O-C Atlas and NASA/IPAC databases for also providing data.We acknowledge with thanks the variable star observations from the AAVSO International Database contributed by observers worldwide and used in this research.We are also grateful to the referees,the editors and everyone involved who provided constructive suggestions and comments for this article.