极限平衡理论下寒区危岩稳定性及关键参数研究现状

2022-09-01舒佳军李小双邓正定黄晶柱

有色金属科学与工程 2022年4期

舒佳军，李小双，b，邓正定*，黄晶柱

（江西理工大学，a.江西省环境岩土与工程灾害控制重点实验室； b.经济管理学院，江西赣州 341000）

寒区是指非极端天气下冬季气温低于0 °C 或冻融深度在0.3 m 以下的地区，我国疆域辽阔，寒区面积约占国土总面积的75%[1-2]。寒区危岩是位于寒区的由多组岩体结构面切割并赋存于陡坡上，在荷载作用下处于不稳定、欠稳定或极限平衡状态的岩块及其组合结构体[3]。寒区危岩主要归纳为两类，第一类为位于寒区自然山体陡坡上，如新疆地区天山和欧洲阿尔卑斯山体上的危岩；第二类则是由于寒区工程活动而形成的，如因矿山开采、大坝开挖等活动形成的岩质边坡上的危岩。近年来，西部矿产资源的开发[4]使得在寒区的岩土工程逐渐增加，危岩稳定性已成为亟须解决的问题。

赋存于寒区危岩中的水分在气温交替变化中不断冻结、融化，反复的冻结和融化过程即冻融循环作用极易引起危岩失稳。资料表明危岩失稳破坏已是寒区的主要地质灾害之一，如阿尔卑斯山西部危岩在冬季遭受强烈冻融循环作用，导致边坡基岩松软碎裂进而出现冻融滑坡事故[5]；西藏甲玛金矿由于长期冻融循环和扰动作用引起岩体劣化，导致200 多万立方米的矿区出现塌方，造成了巨大的人员和财产损失[6]。因此，冻融循环作用下的危岩稳定性分析已成为寒区工程建设的关键问题，深入开展危岩稳定性研究对推动岩质边坡治理、防治地质灾害、保证人民生命财产安全具有重要意义。目前，国内外相关学者对冻融循环作用下的寒区危岩稳定性分析及评价开展了大量研究，考虑到危岩稳定性受多种因素影响，研究方法也相应多样，总体上分为4 类[7]，如表1所列。

表1 危岩稳定性分析方法Table 1 Stability analysis method of dangerous rock

地质法主要通过对危岩地质勘察进而分析其稳定性，其理论基础为地质演化论、地质类比论和岩体结构控制论，该方法只适用于地质条件复杂的各式边坡、危岩的定性分析。极限法有极限平衡法和极限分析法两种，二者均对边坡、危岩潜在破坏面进行简化，定量分析其稳定性变化。数值法是基于微元间的相互影响和作用并反映在宏观尺度上的计算机分析方法，数值计算法将危岩破坏行为视为从联系变形到非联系变形，再到分离的过程，将有限元法等连续介质方法同离散单元法等散体介质结合。可靠性法是考虑到工程设计、施工过程中的不确定因素对危岩稳定性的影响，将不同影响因素视为随机变量并结合分布概率函数模型，基于可靠指标和破坏概率对危岩开展分析[8]。上述危岩稳定性分析方法各有优劣，其中，基于极限平衡理论的分析方法是目前较为成熟且应用普遍的计算方法，该方法主要是在对危岩稳定性进行计算的基础上，以力学分析结果对其稳定性进行评价，能更直观且准确地分析危岩稳定性，具有理论完善、便于计算、结果可靠等优点[9]，并可显示出不同计算参数的影响作用。考虑到危岩失稳模式的差异性，本文将基于极限平衡理论对不同类型的寒区危岩稳定性及参数研究现状展开综述。

1 极限平衡理论下危岩稳定性分析

滑移式危岩失稳破坏是指在荷载作用（主要为自重荷载、水平力荷载和冻胀荷载）下，危岩主控面上抗滑力不足以抵抗下滑力，进而导致不稳定岩块从母岩滑落[10]，故判断滑移式危岩是否出现失稳破坏的核心问题是对其主控面上的作用力进行求解。滑移式危岩计算模型如图1 所示。

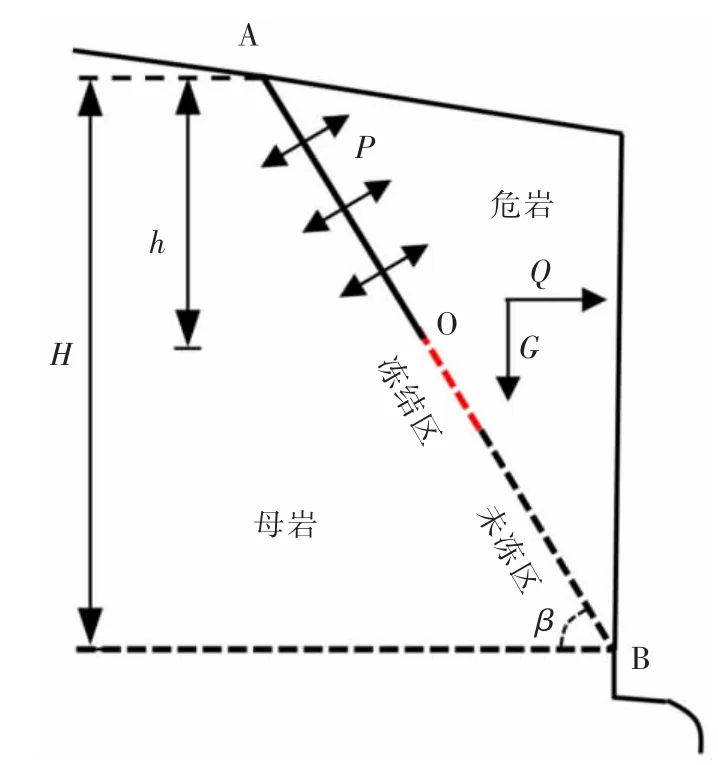
图1 滑移式危岩计算模型Fig.1 Calculation model of sliding unstable rock

图1 中AB 段为危岩主控面，OA 段为主控面上贯通段，通常为结构面；OB 段为主控面上未贯通段，未贯通段又包含冻结区和未冻区；H 和h 分别为危岩竖直距离和贯通段竖直距离；G 为单位长度危岩所受重力；Q 为单位长度危岩所受水平力；P 为贯通段均布冻胀荷载；β 为危岩体结构面倾角。以抗剪强度作为危岩结构面的抗滑力，以主控面上切向力作为其下滑力[11-13]，可得危岩稳定性系数F 为：

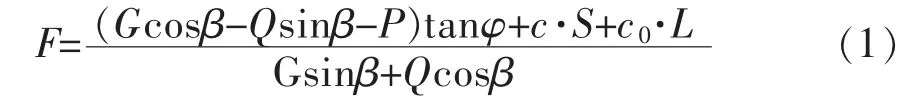
式（1）中：φ 为危岩块内摩擦角；c 和c0分别为冻结区和未冻区岩石黏聚力；S 和L 分别为未贯通段冻结区长度和未冻区长度。

倾倒式危岩失稳破坏是指在荷载作用下，危岩主控面上作用力对倾覆点产生的抗倾覆力矩不足以抵抗倾覆力矩，进而导致危岩块从母岩中倾倒的现象[10]。由于倾覆点存在的位置不同，倾倒式危岩分为内倾式（危岩重心在倾覆点内侧）和外倾式（危岩重心在倾覆点外侧）两类，但二者在极限平衡理论中的稳定性分析原理是一致的，故此处仅阐述内倾式危岩，如图2所示。判断该类危岩是否出现失稳破坏的核心问题是对倾覆点处的倾覆力矩和抗倾覆力矩进行求解。

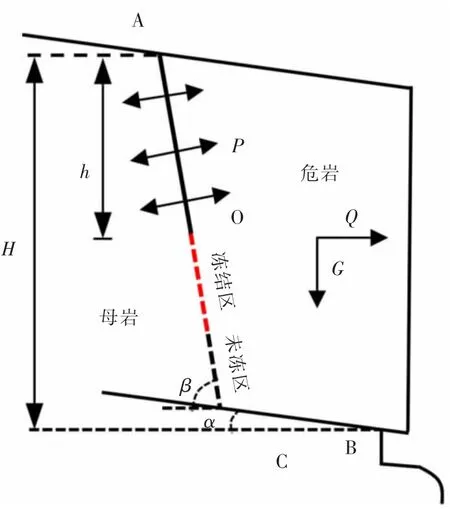
图2 倾倒式危岩计算模型Fig.2 Calculation model of toppling dangerous rock

图2 中危岩重心位于倾覆点C 点内侧，α 为危岩后缘岩石与水平轴线间夹角。由图2 计算模型可知，危岩水平力和主控面上冻胀力在倾覆点产生倾覆力矩，而自重力和未贯通段岩石抗拉强度则提供抗倾覆力矩[14-16]，据此可得倾倒式危岩稳定性系数F 为：

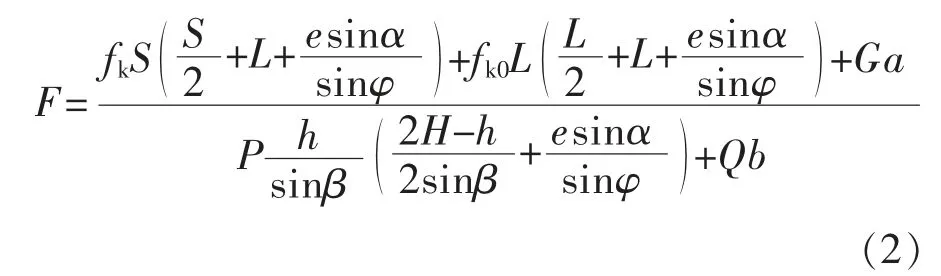
式（2）中：fk和fk0分别为冻结区和未冻区岩石抗拉强度；φ 为危岩倾角与后缘岩体面夹角间差值（φ=βα）；e 为倾覆点至未冻区与后缘岩体交点的水平距离；a 和b 分别为危岩重心至倾覆点C 的水平距离和竖直距离。

坠落式危岩由于自身结构特点，导致其失稳破坏不止由单一条件控制，坠落式危岩既可由主控面抗滑力低于下滑力而破坏，又可由后缘岩体处抗倾覆力矩低于倾覆力矩而破坏，如图3 所示，因此判断坠落式危岩是否被破坏需要综合比较两种条件下的稳定性系数[17-18]。

通过比较危岩破坏控制条件可得坠落式危岩稳定性系数F 为：

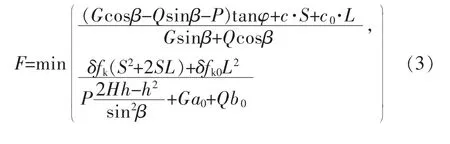
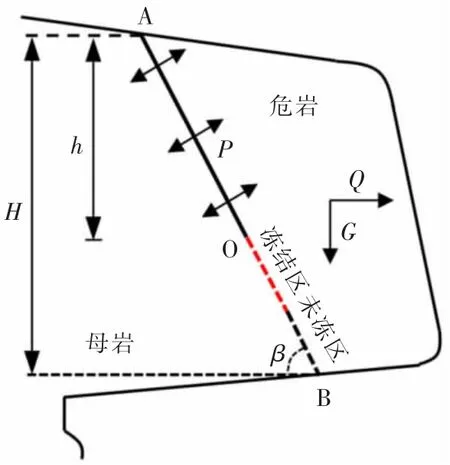
图3 坠落式危岩计算模型Fig.3 Calculation model of falling dangerous rock

式（3）中：δ 为坠落危岩的抗拉力矩计算参数，通常依据破坏面的形态取值，取值范围为1/12～1/6，且当潜在破坏面为矩形时取最大值；a0和b0分别为危岩重心至潜在破坏面的水平距离和竖直距离。

2 危岩稳定性参数研究现状

综合式（1）、式（2）和式（3）可知，利用极限平衡理论对寒区危岩稳定性开展定量分析的核心问题是主控面上各参数的影响效果。冻融循环作用对主控面的影响主要表现在主控面上与岩石物理力学参数，前者包括贯通段所受均布冻胀力、未贯通段冻结深度和未冻深度，后者包括岩石内摩擦角、黏聚力和抗拉强度。

2.1 贯通段结构面冻胀力研究

HUANG 等认为孔隙水冻结引起的冻胀压力是导致岩石破坏的主要原因，为了研究冻融循环作用下岩石冻胀力的长期特性，提出了一种新的弹塑性模型用于估算冻结过程和解冻过程中冻胀压力的发展趋势，进而得出冻胀压力随冻融作用的变化关系[19]。乔趁等对高寒地区锁固段边坡的3 种不同岩桥角度的岩石开展冻胀力分析，发现冻胀力的变化过程包括衍生阶段、陡升阶段、跌落阶段、平稳阶段、融化阶段和消散阶段，并得出了不同阶段下冻胀力的演化曲线[20]。吴永等依托川藏铁路高寒危岩结构面的裂缝，将其简化为半空间平面问题，根据热弹性理论和相关试验数据拟合，得到了贯通段裂缝间的冻胀力解析解，并发现危岩所受冻胀力与裂隙冰体初始温度及温度上升幅度密切相关[21]。乔国文等在研究寒区岩质边坡在冻融条件下的稳定性时，对裂隙水在贯通段产生的冻胀力开展了研究，根据位移－压力理论对水施加的刚性约束模拟岩石约束条件，使其在冻结冰膨胀过程中将膨胀压力传递给液压油，进而测出其冻胀力[22]。刘昊等在探讨寒区裂隙岩体在冻融循环作用下的冻胀力演化规律时发现，每个冻融循环过程中冻胀力都经历孕育阶段、爆发阶段、跌落回稳阶段、回升阶段和消散阶段，并指出出现初始冻胀力峰值时可作为裂隙岩体冻融损伤最劣阶段[23]。胡清义等认为在极端冰雪条件下，冻胀力是影响危岩边坡稳定的重要因素，将冻胀力求解视为半无限体表面受均布力的轴对称问题，引入“等效线弹性系数”，并基于弹性理论求解法向冻胀力的解析解[24]。赵鹏等利用弹性力学理论对冻结的主控面上冻胀力开展研究，通过应力平衡和变形协调得出了结构面尖端的冻胀力计算式，发现影响结构面冻胀力的参数除危岩的弹性模量和泊松比外，还包括贯通段裂缝张开度、冻结温度差和结构面尖端半径等[25]。张永兴等在推导极端冰雪条件下的岩石边坡倾覆稳定系数表达式时给出了贯通段张裂缝对岩壁产生的侧向力计算式，表明冻胀侧向力与张裂隙深度和裂隙面上冰压力呈正比关系[26]。综上所述，结构面贯通冻胀力分析主要归纳为两类，分别为基于现场或室内的裂隙冻胀试验测得及基于裂隙冻胀理论计算所得（如体积膨胀理论、静水压理论、结晶压理论等）。前者适用范围有一定的局限性，并且仅对相关工程的试验对象有效；后者在理论上适用范围广阔，然而考虑到工程环境的复杂性和独特性，同样需要对其进行相应的修正才能运用于计算。

2.2 未贯通段冻结深度研究现状

由于单纯对冻岩深度的研究目前还在进一步探索中，并且在传统的冻土冻结深度计算中是同时包括岩石和土壤[27]，故此处对冻结深度的介绍涵盖了以上二者。文献[28]表明，Robert 在分析坚硬岩石冻结深度的计算方法时，提出了在非均质岩石介质中确定冻结深度的不同因素影响作用，并给出了一种确定岩体冻结深度的通用算法，该算法指出了冻结深度评估的主要因素为渗透系数值、孔隙率、岩石质量指标值（RQD）和Protodiakonow 岩石压实指数。周元辅等在Nelson 的冻结深度计算式和通用的Stephan 经验公式的基础上进行参数化修正，利用岩石参数代替土体参数，得到了通用情况下的岩石冻结深度解析式[29-30]。刘守花等在对季冻区基坑冻结深度研究中考虑热对流和热传导作用的影响，利用Laplace 变换和Laplace 反演推导了基坑冻结温度场的解析解，并利用Matlab 求解其变化规律，结果表明冻结深度与低温持续时间和冻结速率有关[31]。任景全等在研究季节冻土深度随气候变化的响应时，利用东北地区的气象资料对冻结深度进行线性倾向估计拟合，将冻结深度同冻结时间相联系[32]。余宗明综合2 种土体冻结深度的经验公式，提出了一种与冻结负温和时间相关的理想公式，对3 种不同工况下的冻结深度进行比较，得出了理想冻深公式的适用范围[33]。王澄海等利用我国的冻土资料对比了几类常用的冻土冻结深度估算方法，并对估算方法的可靠性进行了讨论，比较结果表明，Stephan 估算法所得冻结深度与实测数据的年变化趋势基本一致，但数值偏差较大；Kudryavtsev 估算法所得冻深在变化趋势与数值上误差均较小，但在部分年份结果与实测结果相差较大；Nelson 估算法在整体上与实测结果保持一致，并且不存在突变数据，是一种较好反映岩土体冻结深度的估算式[34]。可以看出，目前对岩石冻结深度的计算依赖经验公式，通过对当地大量气象资料进行分析，在保证误差允许范围内得出岩石冻结深度表达式。该方法通常能准确预测工程所在地的冻结深度，缺点是无法控制偶然荷载发生时的影响。因此，未来对影响冻结深度的研究可着力于概率分析，通过对不同参数的影响效果及突发频率对原有经验公式开展修正。

2.3 岩石力学性能弱化研究现状

YANG 等认为冻融循环过程中岩石力学性能的变化是影响寒区边坡工程稳定性的关键问题，选取鸭绿江公路边坡岩石开展冻融循环蠕变试验，利用数学分析软件First Optimization 对参数变化识别，结果表明，随着冻融循环次数的增加，岩石的弹性模量、抗拉压强度、黏聚力、内摩擦角及密度均呈下降趋势[35]。LUO 等在对蒙库铁矿岩质边坡稳定性分析时考虑到冻融循环对岩石强度的影响，选取了麻粒岩、角闪麻粒岩、层理麻粒岩及黑云角斜片麻岩的完整岩石开展冻融循环试验，历经30 次冻融循环作用后，4 种岩石的抗拉强度都出现不同程度的弱化[36]。JIA 等通过砂岩的冻融循环监测岩样弹性模量、抗压和抗拉强度，在17 次冻融循环后，岩石抗压强度和抗拉强度分别下降了40%和95%，故冻融循环作用被认为是危岩失稳破坏的主要驱动力[37]。LI 等依据冻融循环试验所得岩石抗压强度弱化程度解释边坡劣化的机理，试验结果表明，岩石平均抗拉强度和弹性模量随冻融次数增加而减小，泊松比则呈先增后减的变化趋势，并采用Hoke-Brown 准则计算冻融循环前后岩石性能弱化对岩坡安全系数的影响[38]。闻磊等对西藏地区玉龙铜矿边坡的灰岩和石英砂岩进行冻融循环试验，并对岩石的抗拉强度变化趋势展开分析，发现冻融循环下岩石抗拉强度的变化趋势与孔隙率密切相关[39]。INCE 等对卡帕多西亚的10 个火山岩试样进行冻融循环试验，将岩石抗拉强度弱化试验结果拟合成强度损失统计模型，该模型可预测岩石不同冻融循环次数下的抗拉强度值，可靠性较高[40]。贾海梁等在研究自然界岩坡的冻融循环损伤时，依据不同冻融周期将“昼夜循环”和“年度循环”分别等效为高周疲劳和低周疲劳，利用疲劳损伤力学将冻融作用的岩石力学损伤以疲劳损伤的方式表征，得到了岩石的冻融损伤解析解[41]。徐光苗等对自然界红砂岩和页岩取样开展冻融循环试验和单轴压缩试验，结果表明，冻融对岩石的压缩强度和弹性模量影响显著，并且由于岩性、矿物成分、孔隙度和含水量等参数的不同，2 种岩样的冻融损伤劣化程度差异也十分显著[42]。郎东明等为探究冻融循环作用对岩石强度影响的机理，通过试验发现随着冻融次数增加，岩石抗压强度和弹性模量均呈指数下降，通过损伤等效原理与Weibull 分布建立损伤本构模型，较好地描述了冻融循环作用对岩石变形和破坏特征[43]。张慧梅等针对寒区工程的冻融受荷岩石岩石，运用损伤力学理论和应变等价原理并考虑岩石细观结构的非均匀性，建立冻融受荷损伤模型，通过损伤模型描述岩石细观结果损伤演化，结果表明，寒区岩石力学性能由冻融因子、荷载因子和耦合效应所决定[44]。陈松等考虑到寒区岩石存在宏观缺陷和细观缺陷，认为冻融与荷载作用引起细观损伤，并在节理岩体上引起宏观损伤，基于Lemaitre 应变等效性假设综合考虑宏细观缺陷进而推导节理岩体的复合损伤模型[45]。文献[46-47]对冻融循环作用下的岩石开展了力学性能弱化有关实验，二者试验结果均表明冻融循环作用会改变岩石抗剪强度参数。综上所述，冻融循环作用对岩石力学性能的劣化效果主要通过现场试验开展，由于岩石材料的多样性和复杂性，从机理上解释其力学性能劣化仍较为困难，因此无法使用解析解对其进行定量分析。近来，利用损伤力学、断裂力学等方法从唯象角度探究岩石冻融劣化工程逐渐成为趋势。

3 关键问题及研究趋势

3.1 关键问题

由式（1）、式（2）和式（3）可知，判断寒区危岩稳定性的关键是明确各参数取值，从上述研究来看，对危岩贯通段冻胀力的计算多是通过理论计算所得，然而不同学者对冻胀力计算的理论基础和假定条件却不尽相同，如基于水冰相变体积膨胀引起的冻胀力计算模型、基于水热迁移引起的分离压力（将分离压力等效为冻胀力）计算模型、基于热力学平衡的冻胀力计算模型、基于弹塑性力学的平面力学计算模型等[48]。对冻结深度参数的获取通常是依靠经验公式或估算式，该类经验公式参数多由气象资料所提供，不同气象点监测数据的差异性对冻深影响极为显著，如常用的Stephan、Kudryavtsev 和Nelson 经验公式在计算青藏高原地区冻结深度时，不同计算式间最大差值达到了20%[34]。对冻融循环作用下岩石力学性能弱化的研究则主要是通过室内试验获取，以砂岩内摩擦角随冻融循环次数变化为例，MU 等[46]开展的冻融试验结果表明砂岩内摩擦角是呈下降趋势，而WANG 等[47]的试验却得出砂岩内摩擦角不随冻融循环次数而改变。因此如何合理地选取计算参数仍是一项亟待解决的关键问题。

3.2 未来研究趋势

1）深入开展寒区工程岩石冻结深度的研究。寒区冻结深度的经验式或估算式多是以冻土为基础，相对于土体，岩石强度高、渗透性低、颗粒黏结强，并且具有孔隙介质和裂隙介质，影响其冻结深度的参数较土体更为复杂。基于多因素之间相互影响及作用的概率分析模型预测可作为未来研究方向。

2）研究多场多相耦合作用下危岩劣化机理。岩石内部存在裂隙、孔隙等结构，在冻融循环条件下，内部存在温度场、渗流场和应力场，场之间的作用相互耦合导致岩石从单一的颗粒结构转换为水—冰—岩—屑等多相多组耦合成的组合结构体，分析冻融循环作用对组合结构体的损伤劣化可揭示危岩破坏机理。

3）开展断裂力学、损伤力学等理论的运用。冻融循环持续作用造成危岩力学性能不断弱化和损伤，如在断裂力学理论中危岩抗拉强度弱化会引起岩石I型断裂韧度下降，抗剪强度弱化会引起Ⅱ型断裂韧度下降，在荷载作用下容易引起I 型或Ⅱ型断裂，故可将危岩断裂韧度视为抗力，将其应力强度因子视为驱动力，应力强度因子与断裂韧度之比则可定义为危岩稳定性系数。