城市快轨交通钢弹簧浮置板轨道过渡段设计分析
2022-09-01李斌强石广田和振兴李鹏浩贠剑峰王玉魁
李斌强,石广田*,和振兴,李鹏浩,贠剑峰,王玉魁
(1.兰州交通大学 机电工程学院,兰州 730070;2.兰州交通大学 甘肃省轨道交通服役环境与智能运维重点实验室,兰州 730070)
近年来,我国城市轨道交通快速发展,由列车运行引起的振动和噪声,严重影响了沿线居民的生活,且对古建筑等造成了破坏,并对精密仪器测试数据造成数据干扰,轨道交通引起的振动和噪声控制问题,已经引起了广泛关注[1-3].轨道减振措施是降低和控制振动与噪声的有效方法,因此,在我国城市轨道交通中获得大量运用.
目前,减振型轨道线路占轨道系统中的比例高于30%,个别线路超过50%[4].因为市场需求较大,各种轨下、枕下、道床下的减振降噪措施,从国外引进、消化、吸收再创新,批量运用.
轨道从普通线路过渡到桥梁,隧道或涵洞前后由于基础结构不同,皆存在刚度不均匀问题.相关试验表明,列车通过刚度突变区时,随即引起的行车动力响应显著增大,由此导致轨道基础结构累积变形逐渐增大,碎石粉化,轨枕空吊,极大地诱发行车安全事故[5].城市轨道交通,由于减振轨道与普通轨道之间的刚度差异,造成轨道的刚度不均;其中普通轨道与钢弹簧浮置板轨道之间刚度差最大.目前国内外学者对路桥[6-8],路隧[9-10],有砟轨道与无砟轨道[11-12]如何过渡问题研究较多.但在城市轨道交通中,由于减振而引起的轨道刚度过渡问题,近几年才开始展开研究[13-16].这是由于部分城市新修线路列车运营速度逐步提高,一般在120 km/h以上.由于轨下刚度差异,导致列车动力响应过大等问题凸显.
100 km/h~120 km/h的城轨列车普遍称为地铁车辆;120 km/h~160 km/h的城轨列车称为快轨.目前国内港铁屯马线,港铁机场快线,港铁东涌线,成都地铁17,18号线,温州轨道交通S1线的运营速度为120 km/h~160 km/h.北京地铁大兴机场线,广州地铁18号线的运营速度为160 km/h.
从城市轨道交通的发展趋势来看,列车运营速度超过120 km/h的线路越来越多.城市快轨交通减振轨道线路刚度参数,如何合理取值?过渡方式如何设置?已成为技术难题.这方面的研究文献相对较少.基于此,建立地铁A型车-钢弹簧浮置板过渡段线路动力学模型,探讨列车时速160 km/h条件下不同过渡段长度、级数、刚度技术指标工况下列车-轨道系统的动力响应,为研究列车-减振轨道过渡段线路系统的动力响应过大问题,提供理论依据.
1 建立车辆-轨道耦合动力学模型
车辆和轨道间的轮轨相互作用是动态的,是复杂的动力学问题.基于车辆-轨道耦合动力学理论[5],将车辆和轨道作为一个相互影响,相互作用的大系统进行研究.车辆-普通轨道-过渡段-钢弹簧浮置板轨道示意图如图1所示.
车辆选用我国城市轨道交通中应用比较广泛且轴重较大的地铁A型车辆.基于车辆-轨道耦合动力学理论建立车辆系统的多刚体动力学模型,其中车体,转向架和轮对用刚体模拟,不考虑其塑性变形;用二系悬挂连接车体与转向架,用一系悬挂连接转向架与轮对.如图1车辆子系统模型所示.详细车辆参数见文献[5].地铁A型车主要参数见文献[17].
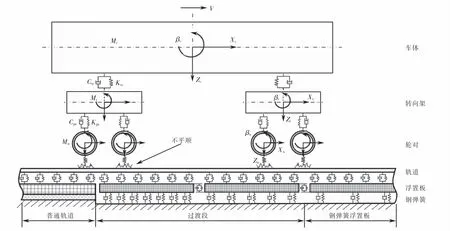
图1 车辆-普通轨道-过渡段-钢弹簧浮置板轨道Fig.1 Vehicle-general track-transition section-spring-steel floating slab
基于动力学软件,建立轨道系统模型,其中钢轨按连续弹性离散点支承上的无限长Timoshenko梁考虑,轨下基础按实体单元考虑,扣件支点和隔振器支点按弹簧阻尼单元考虑.为了准确反映由于轨下基础刚度差异引起的车辆-轨道系统的动力响应,模型中忽略轨道不平顺影响因素.轨道系统的参数如表1所示.
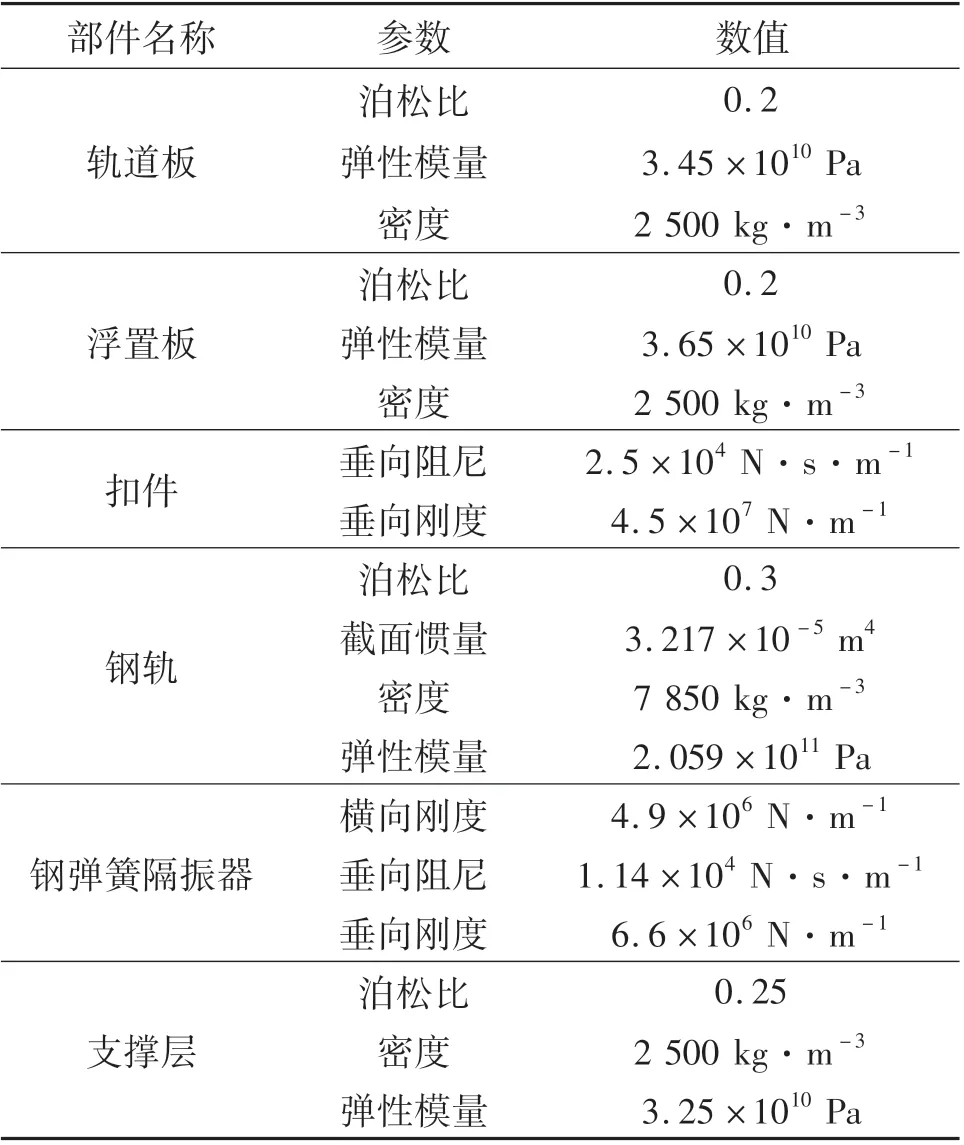
表1 轨道参数Tab.1 Track parameters
车辆系统与轨道系统基于Hertz非线性弹性接触理论,进行模拟轮轨间的接触关系.Hertz非线性弹性接触模型具体表达式如式1所示.

2 钢弹簧浮置板轨道过渡段动力特性分析
2.1 动力学评价指标的选取
由于轨下基础刚度突变会导致车辆-轨道系统动力响应过大,因此在设计过渡段时应选取合适的评价标准,对过渡段的动力性能进行评估.“钢轨挠度变化率”(钢轨动挠度曲线的斜率)可以有效评价轨下基础刚度差引起的轮轨动力作用,也是评价轨道过渡段动力学性能的综合指标.将其控制在0.3 mm/m以内时,可以保证轨道过渡段具有良好的动力学性能.
为了准确评估城市轨道交通列车通过过渡段时车辆轨道系统的动力响应,参照《高速铁路工程动态验收技术规范》(TB10 761-2013)选取车体垂向加速度,轮轨垂向力,钢轨挠度变化率作为评价分析指标.列车时速在160 km/h时规范具体数值如表2所示.
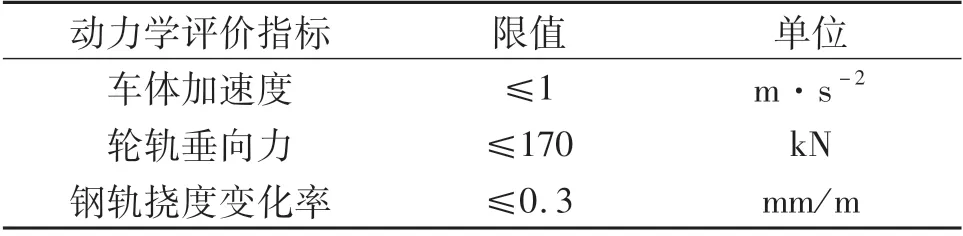
表2 动力学评估指标限值Tab.2 Dynamics evaluation index limits
2.2 过渡段长度对车辆-轨道耦合动力特性的影响
常用的钢弹簧浮置板轨道过渡段设计方案是在两种轨道线路之间增加一段纵向和横向加密钢弹簧隔振器的缓和轨道过渡线路.但是,过渡段长度如何选取?确保车辆-轨道动力学响应满足规范要求.
采用分别设置一块板长,两块板长,三块板长,四块板长的过渡段的研究方法,其中一块板长约6 m,即研究过渡段长为6 m,12 m,18 m,24 m的条件下,列车通过不同长度过渡段时车辆-轨道系统的动力响应.
普通钢弹簧浮置板隔振器一般布置为沿中线对称左右1 m各一个,纵向1.2 m一个.过渡段钢弹簧隔振器加密为纵向间隔0.6 m,横向0.5 m,图2所示为两块钢弹簧浮置板轨道过渡段隔振器加密布置图,其余长度加密方式都与此方式相同,即一半为横向、纵向加密;一半纵向加密.
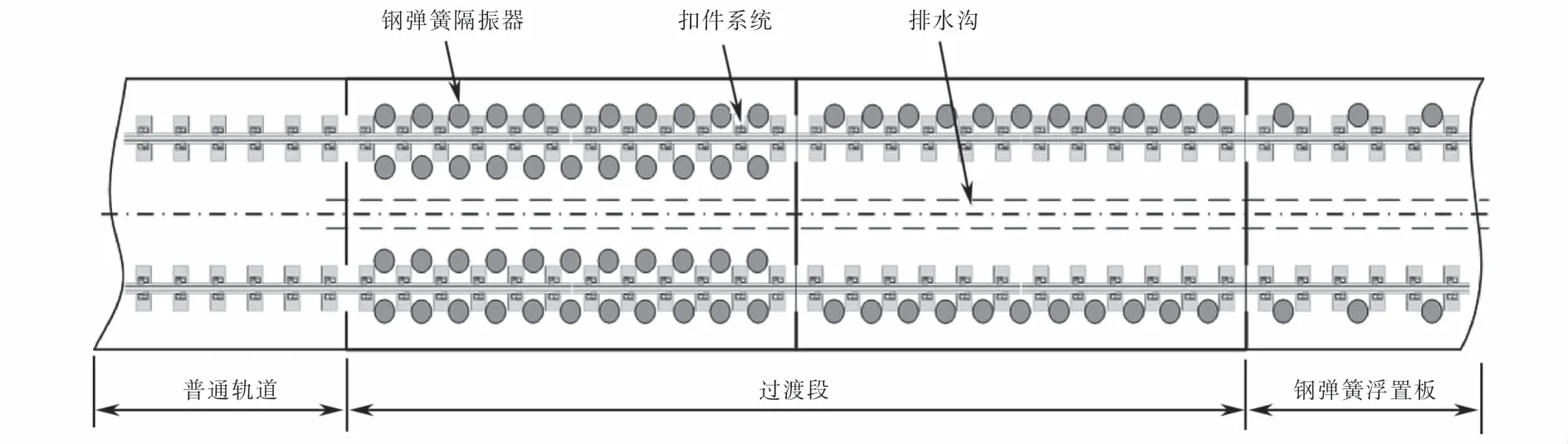
图2 过渡段布置方式Fig.2 Transition section setting method
图3所示分别为不同过渡段长度条件下,车辆-轨道系统的动力学响应图.从图中可以看出在不铺设过渡段工况下,钢轨垂向位移从普通轨道的0.5 mm突变为4 mm左右,车体垂向加速度从0.183 m/s2激增到0.475 m/s2,严重降低了车辆舒适性以及钢轨寿命.
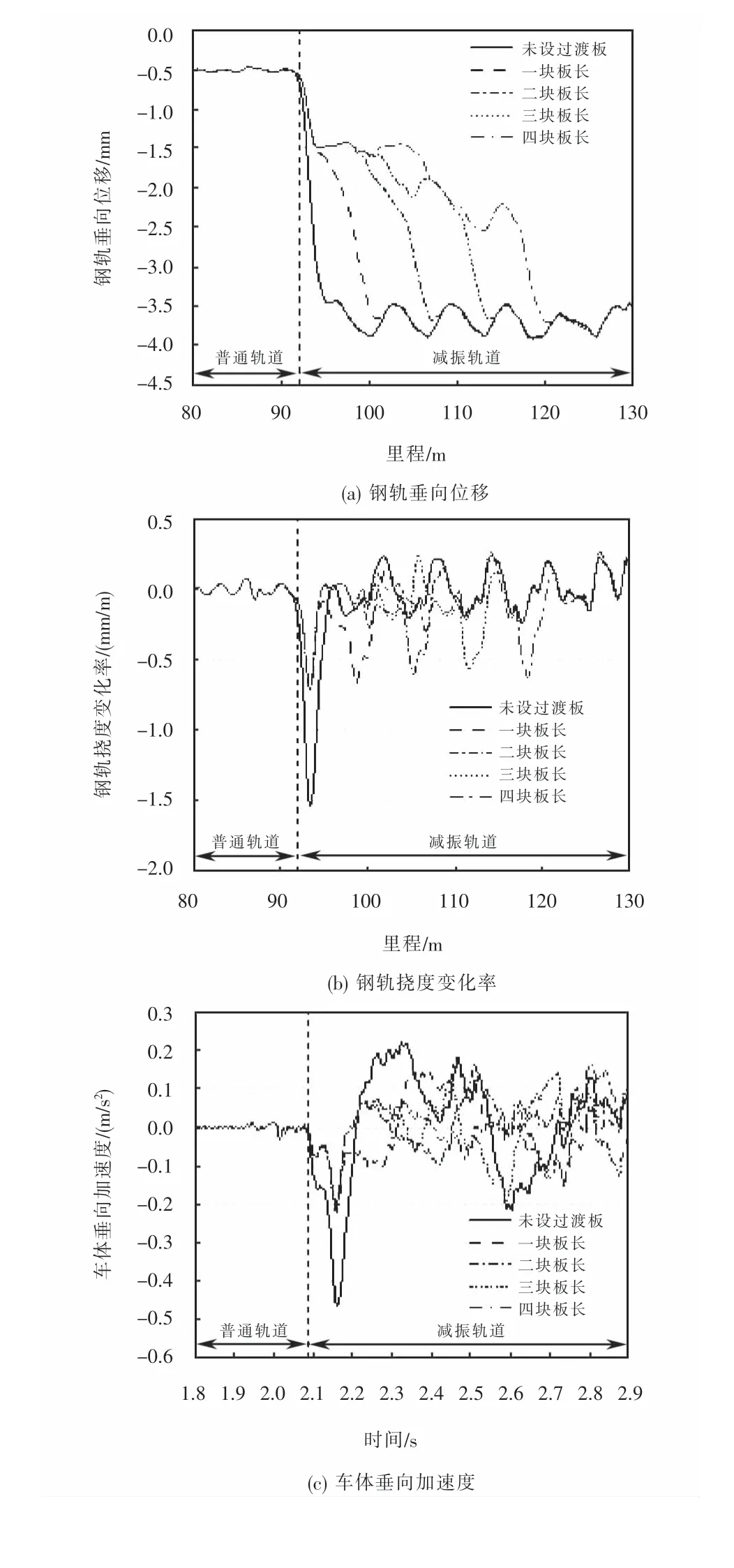
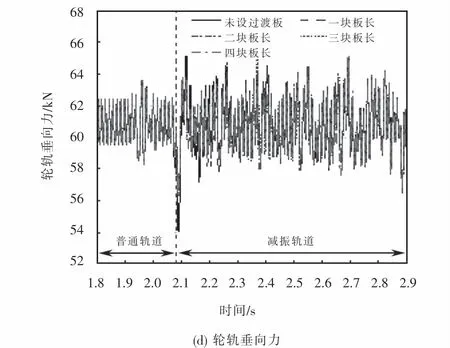
图3 过渡段长度对动力学评价指标的影响Fig.3 Effect of transition section length on dynamics evaluation index
当铺设过渡段后,钢轨位移分级缓和过渡.铺设6 m和12 m长过渡段时,前转向架在后转向架未驶入过渡段时已经通过两次刚度突变区,对车辆系统的影响较大.在未铺设过渡段时,车体加速度也有比较大的影响,最大为0.462 m/s2,在铺设过渡段后最大响应为0.219 m/s2,降幅52.6%,车体加速度在未铺设过渡段条件下,满足规范要求.
从图3中(d)可以看出是否铺设过渡段,对轮轨垂向力影响较小,列车由普通轨道驶向钢弹簧浮置板时,轮轨垂向力有所激增,但是幅值不大,满足规范要求.在铺设过渡段后轮轨垂向力得到了有效地控制,降幅33.3%.相对于钢轨挠度变化率和车体加速度两个指标,过渡段对轮轨垂向力的影响不是很大,因此在后续章节中不再讨论对轮轨垂向力的影响.
综合来看,四块板长的过渡段过渡效果最好,但是和三块板长的过渡段区别不是很大,从工程效益角度出发,选取三块板长的过渡段设计方案.
2.3 过渡段加密程度对车辆轨道动力特性的影响
过渡段设计的思路是两端基础刚度值与相连接轨道刚度值相近,效果最好.考虑到普通轨道刚度较大,钢弹簧浮置板刚度较小,按照上述思路,根据隔振器实际大小,将第一块板钢弹簧隔振器加密到纵向每0.4 m一个,第二块板隔振器纵向每0.6 m一个,第三块板纵向每0.8 m一个,布置方式和上一节相同.同时设置第一块板隔振器0.4 m加密,第二,三块板隔振器0.6 m加密和第一,二块板隔振器0.6 m加密,第三块板隔振器0.8 m加密的两组工况.
从图4可以看出,分级加密以后,钢轨挠度变化率和车体加速度都得到了良好的控制.其中,动力响应最优的设计方案是0.4 m+0.6 m+0.8 m的布置方式.0.4 m+0.6 m,0.6 m+0.8 m和0.4 m+0.6 m+0.8 m的布置方式在驶入过渡段时钢轨挠度变化率降低幅值分别为62.0%,51.8%和62.0%.车体加速度降低幅值分别为66.5%,55.3%和66.5%.由于刚度差的原因,0.4 m+0.6 m的布置方式在驶出过渡段时,钢轨挠度变化率和车体垂向加速度的响应均比其他两组工况较大.
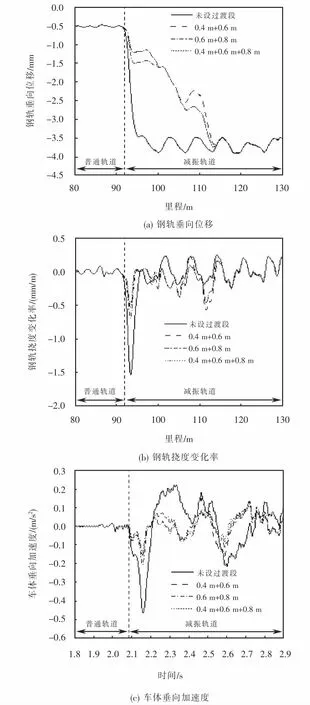
图4 钢弹簧加密对动力学评价指标的影响Fig.4 Effect of steel spring encryption on dynamic evaluation index
2.4 变刚度过渡段对车辆轨道动力特性的影响
分级加密后,钢轨挠度变化率性能指标依然超出规范要求,主要原因是由于两种不同轨道之间刚度差值较大,所以本节在上一节的基础上,改善部分钢弹簧浮置板的隔振器刚度值,以减小两块板之间的刚度差.
为了兼顾驶入过渡段浮置板隔振器刚度值与普通轨道刚度值相近,驶出过渡段刚度值与浮置板隔振器刚度值相近,提出以下三种设计方案.1)第一块板钢弹簧刚度值提升为普通钢弹簧的3倍,第二块板提升为2倍,第三块板刚度值不变;2)第一块板钢弹簧刚度值提升为普通钢弹簧的6倍,第二块板提升为4倍,第三块板提升为2倍;3)第一块板钢弹簧刚度值提升为普通钢弹簧的7倍,第二块板提升为4倍,第三块板刚度值不变.
从图5可以看出变刚度过渡段对钢轨挠度变化率起着很好的控制作用,3k+2k+1k,6k+4k+2k,7k+4k+1k三种设计方案在第一刚度突变区的挠度变化率分别是0.324 mm/m,0.227 mm/m和0.213 mm/m,降幅分别为80.0%,86.0%和86.9%.车体垂向加速度从未铺设过渡段的0.463 m/s2分别降低到0.071 m/s2,0.044 m/s2和0.040 m/s2,降低幅值分别为84.7%,90.5%和91.4%.

图5 钢弹簧刚度对动力学评价指标的影响Fig.5 Influence of steel spring stiffness on dynamic evaluation index
对比三种变刚度过渡段铺设方案,虽然6k+4k+2k,7k+4k+1k的工况在第一刚度突变区挠度变化率符合设计规范标准,3k+2k+1k工况下稍微超出一些,但是6k+4k+2k,7k+4k+1k的工况提升刚度后带来了另外两个刚度突变区.使得钢轨挠度变化率和车体垂向加速度在另外两个突变区有较大响应.因此最优的解决方案是3k+2k+1k.
从图5(b)可以看出,钢轨挠度变化率在105 m和112 m处有两个较大的突变,这是由于二,三块板之间和三,四块板之间提升刚度带来的刚度差造成的挠度变化率突变.因此将第三块板前加密四个钢弹簧隔振器,第四块板为钢弹簧浮置板,为了降低驶出过渡段时的刚度差,因此在第四块板前加密两个隔振器.整体布置如图6所示.
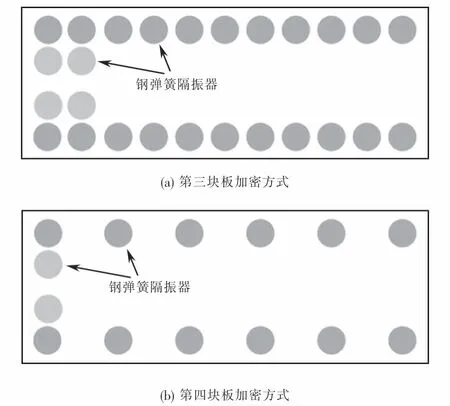
图6 过渡段设置方式Fig.6 Transition section setting method
从图7可以看出,调整后的过渡段在列车通过过渡段后,钢轨挠度变化率得到了很好的控制,且性能满足技术规范要求.

图7 钢轨挠度变化率Fig.7 Change rate of rail deflection
2.5 不同速度条件下车辆-轨道动力特性的响应
为了讨论不同时速条件的列车通过过渡段时的车辆-轨道系统的动力响应,设置80 km/h,100 km/h,120 km/h,140 km/h,160 km/h五组工况进行研究.
从图8可以看出铺设过渡段后钢轨挠度变化率,在不同车速条件下动力响应区别不是很大,高速列车相较低速列车挠度变化率较小.随着车速的增加,车体加速度的动力响应逐渐增大.
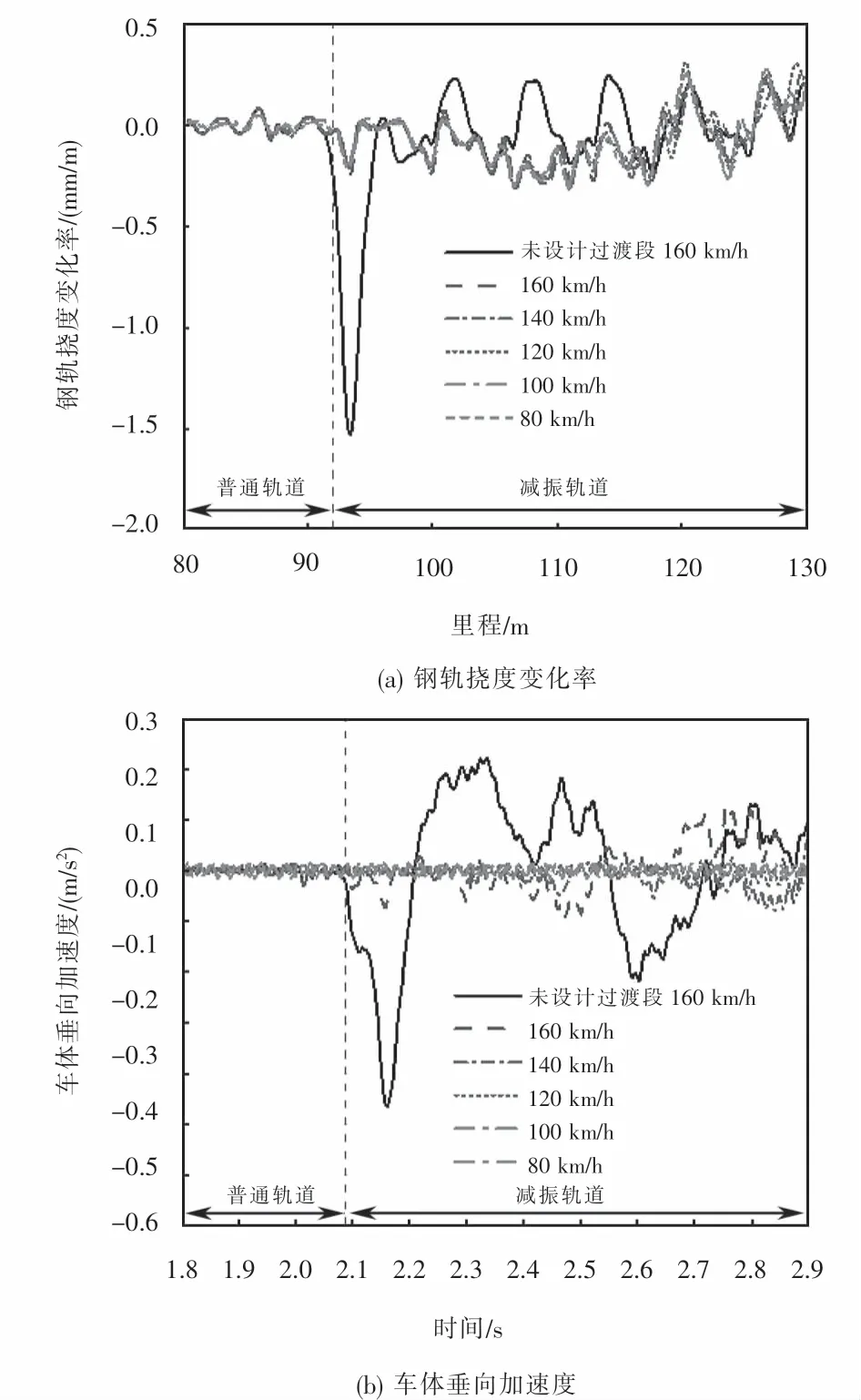
图8 不同行车速度下车辆-轨道动力学响应Fig.8 Vehicle-track dynamic response at different speeds
3 结论
基于车辆-轨道耦合动力学理论,建立了车辆-普通轨道-过渡段-钢弹簧浮置板轨道动力学模型,讨论了过渡段在不同长度,加密程度和刚度的工况下,车辆-轨道系统的动力学响应,并得出以下结论:
1)在未铺设过渡段时,钢轨挠度变化率动力响应超过设计规范标准要求,所以应该铺设钢弹簧浮置板轨道过渡段,铺设长度大于等于18 m.
2)分级变刚度和线性加密钢弹簧浮置板隔振器是铺设轨道过渡段的最优解决方案,钢轨挠度变化率和车体垂向加速度在铺设过渡段后均得到有效控制.
3)由于变刚度分级过渡以及出过渡段时存在一定的刚度差,因此在设置过渡段时不仅应该考虑驶入过渡段,还应该考虑驶出过渡段时的情况.
4)不同车速条件下,在通过过渡段时,随着车速的增加,钢轨挠度变化率逐渐降低,车体加速度逐渐增大.
