基于电化学阻抗特征选择和高斯过程回归的锂离子电池健康状态估计方法

锂离子电池因具有高能量密度、高功率密度、长寿命等优点，已广泛应用于消费电子品、电动汽车、智能电网等领域

。电池在使用与存储过程中，内部会发生一系列副反应，导致活性物质与电解液减少，电池容量衰减，电池内阻增加，健康状态(state of health，SOH)逐渐劣化

。锂离子电池SOH 是实现电池状态估计、剩余使用寿命预测的关键参数，但由于电池老化机理复杂，影响因素众多，如何精准估计SOH仍面临巨大挑战

。

目前，锂离子电池SOH 估计方法可大致分为两类

：基于电池模型的估计方法和基于数据驱动的估计方法。前者以电化学机理模型

或等效电路模型

为基础，结合扩展卡尔曼滤波

、粒子滤波

等方法，实现SOH估计。后者采用模糊逻辑

、人工神经网络

、高斯过程回归(Gaussian process regression，GPR)

等方法，基于电流、电压时序测量数据，构建SOH 估计模型。相较而言，数据驱动法计算复杂度低、灵活性好，但受训练样本的数据规模和质量影响较大。需要指出的是，现有数据驱动方法大多基于时域电流、电压响应曲线数据，实施特征提取，构建SOH 估计模型。因此，当电池实际使用工况与实验测试工况不匹配时，容易出现模型精度下降甚至失效等问题。

相比于时域电流、电压响应曲线数据，基于频域的电化学阻抗谱(electrochemical impedance spectroscopy，EIS)由于蕴含了电池内部丰富的材料特性、界面现象和电化学反应等信息

，可以从多角度反映电池的老化状态，被认为是一种实现SOH估计的有效手段

。目前，利用EIS数据进行SOH 估计时，主要采用两种方式：一是通过构建频域等效电路模型建立特征参数与SOH 的定量关系模型

。该方法能够直观模拟电极反应过程中的动力学行为，但无法完全反映电池老化过程中的物理、化学变化历程

，因此可靠性难以保证；二是采用数据驱动方法

构建EIS数据与SOH的定量关系模型。这种方法可有效避免求解频域等效电路模型构建的复数非线性优化问题，在线应用可行性高。但由于不同频率阻抗数据间往往存在非线性相关性，直接采用全频段EIS 数据构建SOH 估计模型，精度通常受限。此外，开展全频段EIS 测试，需耗费大量时间，实际应用存在一定困难。因此，如何从全频段EIS 数据中优选与SOH 密切相关的阻抗特征子集，是亟需解决的关键问题。鉴此，本文提出了一种基于电化学阻抗特征选择和GPR 的SOH 估计方法，结合序贯前向搜索(sequential forward search，SFS)策略和水平图(level diagrams，LD)多目标决策方法，实现了对全频段电化学阻抗的特征优选，基此构建了SOH 估计模型，并与多种特征选择策略进行了性能比较，从模型复杂度及模型精度方面对所建模型进行了验证。

石化青年一代用“爱我中华、振兴石化”的理想点燃自己的青春梦想，肩负起时代赋予的特殊使命，为“中国梦、石化梦、我的梦”创造青春奇迹。

1 基于特征选择和高斯过程回归的SOH估计

本研究提出了一种基于特征选择和GPR 的SOH 估计方法。通过SFS 策略，结合交叉验证均方根误差指标，从全频段EIS阻抗特征集合中逐步优选包含不同数量特征的阻抗特征子集。在此基础上，为均衡模型复杂度与模型估计精度，综合考虑了特征个数与交叉验证均方根误差两种评价指标，优选得到一组最优特征子集。最后，以最优特征子集作为输入项，构建GPR模型实现对电池SOH的精准估计。所提方法的流程示意图如图1。

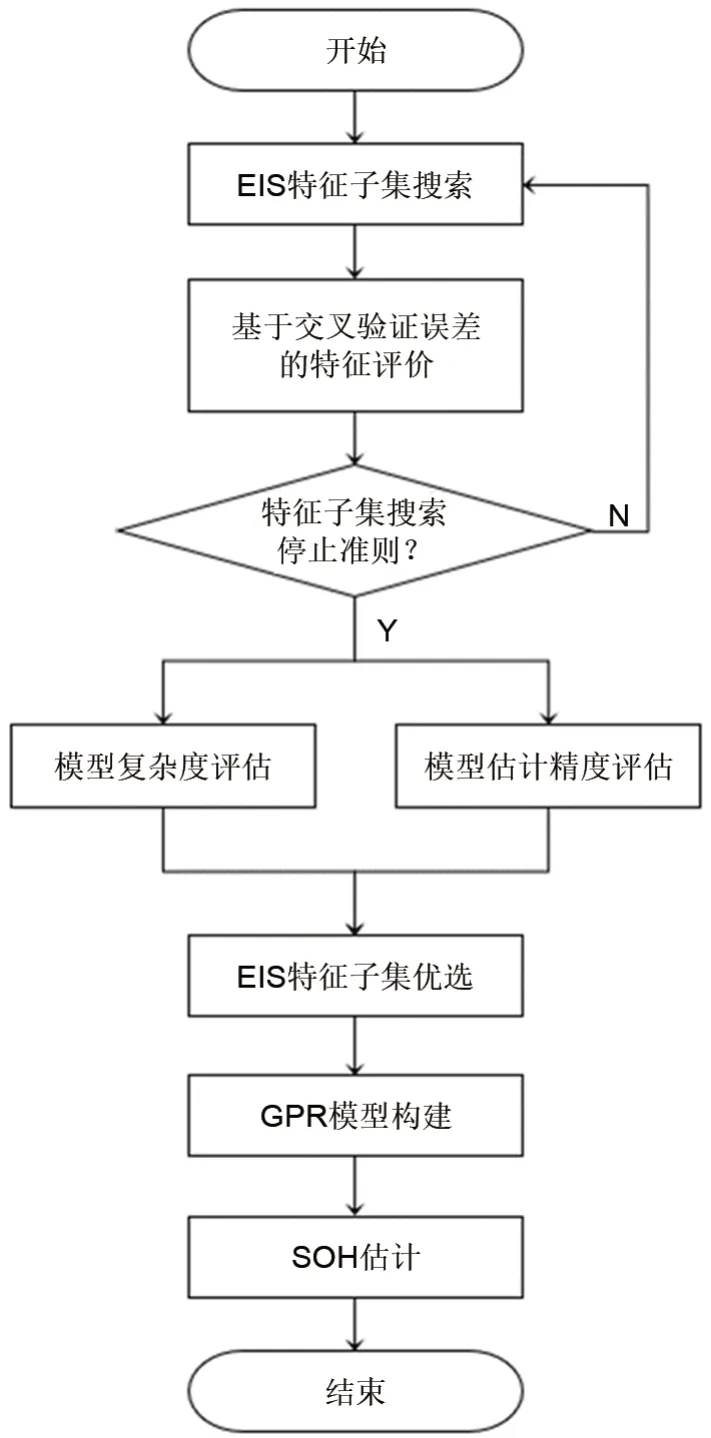
1.1 SOH估计问题描述

开展电池老化循环与电化学阻抗谱测试，在

个不同老化状态下，测得

个频率下的全频段EIS数据，组成集合

={

x

,

= 1,2…2

}，其中，

x

=[

…

z

]

，

z

为单个频率下的阻抗实部或阻抗虚部；电池的SOH 数据组成集合

={

}，其中，

y

=[

…

y

]

，

y

为电池SOH，表示为电池当前最大可用容量

C

与其初始状态下的容量

之比

，计算公式如式(1)所示：

玉玦引发的细微的一点变化，让少年们觉得心头一动，好像由今夜开始，积雪终会融化，榆树会抽出新枝，黄梁村谷仓里的小麦与高粱要做好发芽的准备，秦岭之中的草木也将重返春光，秦岭之外，黄河得到了破开冰凌的勇气，那些将要打破潼关的恶贼，他们的好运，也决不会出现。

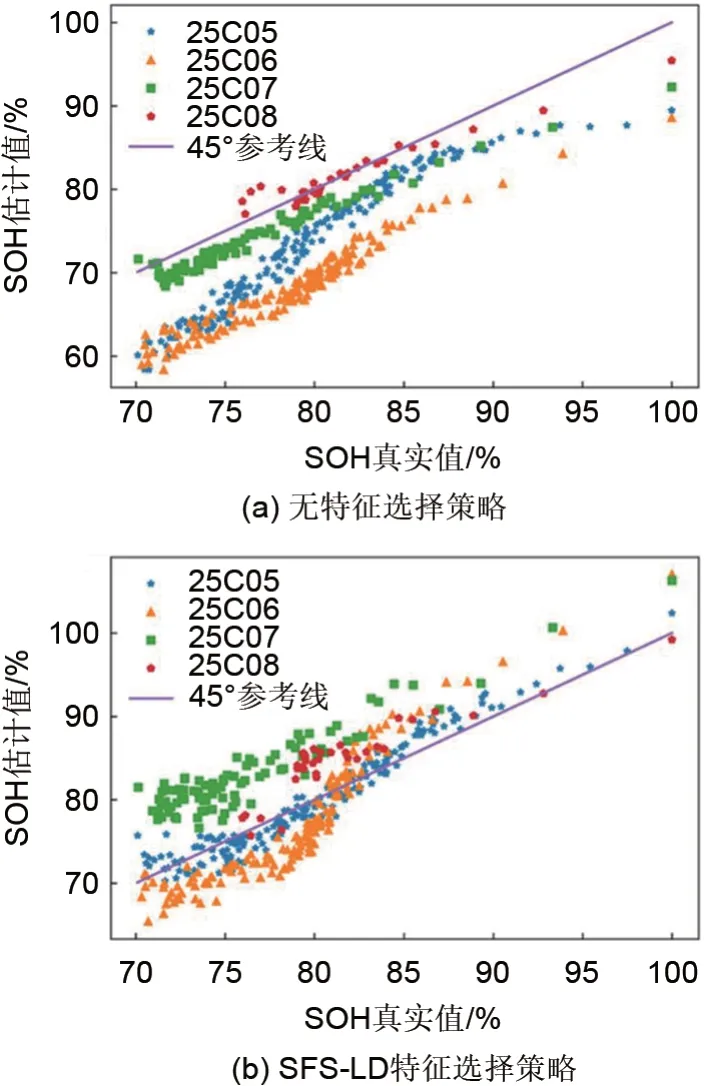
由图6(a)可知，直接将全部阻抗数据作为GPR模型的输入变量，测试集上25C05～25C08号电池的SOH 估计误差RMSE 约为7.5%，模型的SOH估计误差偏大。这一结果表明，不经特征选择直接基于全频段EIS 数据构建的SOH 估计模型精度较低，难以满足实际应用需求。从图6(b)中可见，相较于图6(a)中无特征选择策略，引入SFS-LD 策略后，模型SOH 估计精度显著提升，测试集上25C05～25C08 号 电 池 的SOH 估 计RMSE 约 为4.2%。图7对比了引入SFS-LD策略前后25C05号电池在不同循环次数下SOH 的估计结果。由图7可知，无特征选择策略的SOH 估计模型在全生命周期内对SOH存在显著低估，SOH估计RMSE约为6.9%，相反，基于SFS-LD 策略的模型SOH 结果与实际测得SOH 数据较好相符，SOH 估计RMSE仅为1.6%。

1.2 EIS特征子集搜索

特征子集搜索策略按照特征子集生成过程可分为全局最优、随机搜索和启发式搜索3 种

。启发式搜索法相较于其他两种方式，具有搜索空间较小，易于实现且计算效率较高等优点，因此，本文选择启发式搜索中的SFS 策略进行阻抗特征选择。同时，考虑到阻抗数据的高维度特点，在SFS搜索过程中，结合GPR构建SOH估计模型。GPR是基于贝叶斯理论和统计学习理论发展起来的一种机器学习方法，具有容易实现、超参数自适应获取以及输出具有置信区间等优点，适用于高维度、非线性的复杂回归问题，已被广泛应用于时间序列预测分析和动态系统模型辨识等领域

。基于所提SFS与GPR相结合的方式，本文对电池全频段EIS数据实施特征子集搜索，具体过程如下：

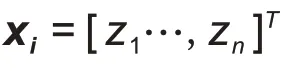
图4(a)所示为基于训练集数据进行特征选择过程中，模型估计误差随优选特征个数的变化曲线。横轴表示特征子集包含的特征个数，纵轴表示基于优选特征子集构建GPR 模型的SOH 估计RMSE。从图中可见，在SFS 搜索过程中，模型交叉验证RMSE整体上呈现先下降后上升的趋势。当特征个数从1 增加至20 时，模型交叉验证RMSE 由0.23%显著降低至0.03%；当特征个数从20 进一步增加至61时，模型交叉验证RMSE虽略有降低，但变化幅度不大，RMSE最低为0.02%；而随着特征个数继续增加，模型交叉验证RMSE呈现显著上升趋势。由此可见，特征子集包含的特征个数直接影响模型估计精度。当特征个数较少时，所建模型难以充分描述SOH 的复杂变化趋势，误差较高。而当选入的特征个数过多时，其中潜在的无关变量可能会使得模型性能劣化。

图2 为25C01 号、25C05 号电池SOH 随 循 环次数变化趋势曲线，从图中可见，两只电池老化速率存在显著差异。25C01 号电池在循环初期，SOH 衰减较为缓慢，循环300 次后SOH 值仍高于70%；25C05 号的电池，在循环初期SOH 衰减速率稍快，当循环次数接近400 次时出现了跳水现象。鉴于电池SOH 到达70%以下时已难以继续使用，因此，本文采用100%～70% SOH 区间内的数据评估所提算法性能。

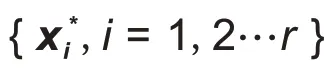
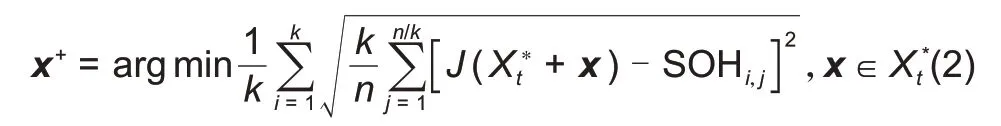
1.3 EIS特征子集优选

1.4 SOH估计模型构建

2 结果与分析

2.1 电池老化与电化学阻抗测试数据集

为考察所提SOH 估计方法性能，本研究采用

上 公 开 发 表 的45 mAh 商业纽扣电池(正负极活性材料分别为钴酸锂和石墨)老化电化学阻抗数据集

对其进行验证，电池编号为25C01～25C08，老化环境温度为25 ℃。每个老化循环包括充电、放电两个阶段：在充电阶段，先以1 C 倍率恒流充电至截止电压4.2 V，再恒压充电到电流衰减至0.1 C，最后静置15 min；在放电阶段，先以2 C 倍率恒流放电至截止电压3 V，之后静置15 min。电化学阻抗谱测试在充放电循环偶数次实施，频率范围为0.02 Hz～20 kHz，激励电流幅值为5 mA。上述电池测试数据划分为训练集和测试集两部分，其中25C01～25C04号电池测试数据作为训练集，25C05～25C08号电池测试数据作为测试集。采用训练集数据的均值和方差对全部数据进行Z-Score归一化处理。

中共中央办公厅、国务院办公厅2015年印发的《深化农村改革综合性实施方案》提出：“必须坚守土地公有性质不改变、耕地红线不突破、农民利益不受损‘三条底线’，防止犯颠覆性错误。”习近平总书记2016年在安徽省凤阳县小岗村主持召开农村改革座谈会时强调：不管怎么改，不能把农村土地集体所有制改垮了，不能把耕地改少了，不能把粮食生产能力改弱了，不能把农民利益损害了。④农村土地经营权物权化不违背农村土地制度改革的原则和底线，能强化集体所有权、提高耕地利用率、保障和增加农民利益，具有现实可行性。

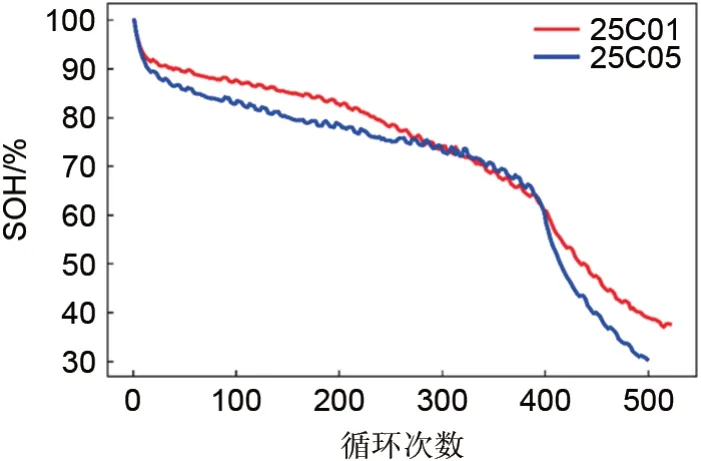
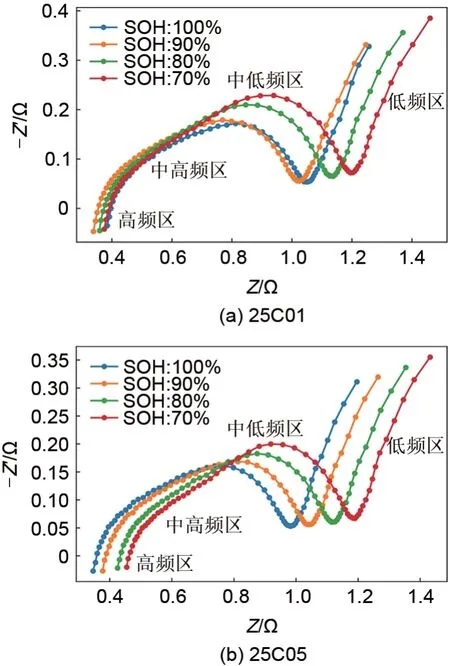
图3所示为25C01号电池、25C05号电池在不同SOH下的EIS曲线对比图。由图3可见，除极个别曲线外，随着电池SOH 的降低，高频区EIS 曲线整体向右移动。其原因可能在于，高频区EIS曲线与实轴交点近似为电池内部的欧姆内阻

，随着老化的进行，电解液因所参与副反应逐渐减少，液相传质阻力上升，欧姆内阻升高，从而导致高频区EIS 曲线整体向右移动。EIS 曲线在中高频区与中低频区存在两个圆弧，并且随着电池SOH的降低，呈现出扩大趋势。一般地，中高频圆弧与中低频圆弧被认为分别对应电池内部固体电解质界面阻抗以及固液界面电化学反应阻抗

，随着老化的进行，固体电解质界面阻抗以及固液界面电化学反应阻抗逐步增加，圆弧半径随之扩大。低频区EIS曲线表征了电池内部的固相扩散过程，随着电池SOH 的降低，低频区阻抗实部和虚部整体上呈增大趋势。

2.2 基于SFS-LD策略的特征子集优选结果

步骤二：数据驱动模型构建。构建基于GPR的数据驱动模型，采用径向基函数作为GPR 的核函数，核函数中的超参数通过极大似然估计进行优化。

为验证所提SFS-LD 策略对模型SOH 估计精度的提升效果，本研究对比了引入SFS-LD策略前后模型SOH 估计的结果。分别采用无特征选择策略的SOH 估计模型、基于SFS-LD 策略的SOH 估计模型，对测试集上25C05～25C08 号电池进行SOH估计，结果如图6所示。

科技创新政策清理指的是针对创新环境、创新客体等已经发生改变从而导致政策本身已经难以推动当前社会的创新发展，政策的继续执行成本大于收益，而且还会给社会创新环境造成不良影响的政策进行修订、废止等措施，从而提高科技创新政策的科学性，提高我国科技创新水平。

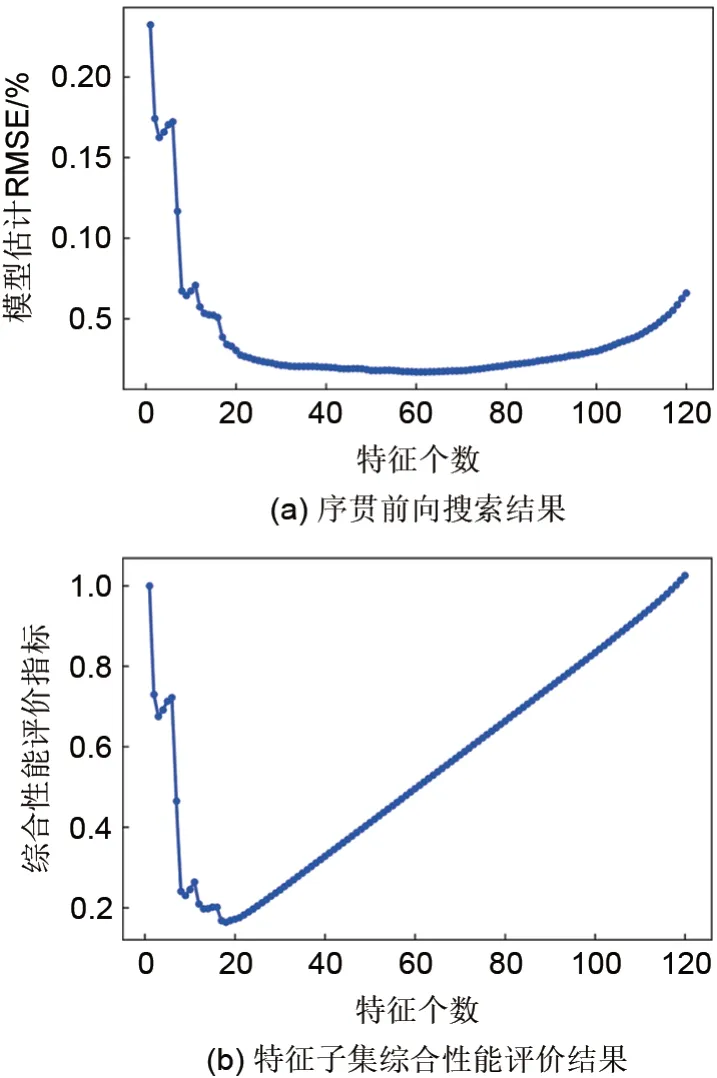
图5所示为基于SFS-LD策略优选得到的18个特征的频段分布图。从图中可见，优选所得特征在高频、中频和低频区均有分布。最终优选的特征子集中包含低频区(0.02 Hz 与0.064 Hz)的阻抗实部，中低频区(22～2.2 Hz)的阻抗虚部，中高频区(5～1.5 kHz)的阻抗虚部，以及高频区(20～16 kHz)的阻抗虚部。其中，低频区数据主要与固相扩散阻抗相关，中低频区与中高频区数据主要反映了固液界面的反应与传递阻抗，高频区数据则与溶液内阻相关。电池老化过程中，上述各频段下的阻抗会呈现一定的演化规律，均能在一定程度反映电池的老化状况。优选得到的关键特征较好地保留了不同频段的阻抗响应特性，同时也有效剔除了过多的无关特征，从而为精准SOH估计提供了保证。

2.3 基于SFS-LD策略的SOH估计模型性能验证

2.3.1 模型SOH估计精度的提升效果验证

进一步地，采用LD 方法对SFS 搜索得到的一系列特征子集进行优选，其结果如图4(b)所示。横轴为特征子集包含的特征个数，纵轴表示特征子集的综合性能评价指标，指标值越小，表明模型能以较小复杂度实现较高精度的SOH 估计。从图中可见，随着特征个数的增加，综合性能评价指标整体上呈现先降低后升高的趋势。当特征个数为18时，综合性能评价指标最小，为0.16。因此，后续采用优选得到的18 个特征作为SOH 估计模型的输入数据。

在大风浪中，船舶颠簸摇摆，旅客站立和行走都比较困难，尤其是通道上一旦洒落茶水或者其他液体，即使清理也会打滑。因此尽量要求旅客不要随意走动，以免不慎跌倒。如果旅客有事走动，海乘人员应该辅佐或告诫旅客随着颠簸摇摆的节奏和幅度缓慢行走。旅客随身携带的行李因少有固定，容易移动、倒塌和翻滚。笨重的行李可能会在摇摆的惯性下伤及人员。因此，必须在开航前严格检查行李和货物是否绑扎和加固好，航行中经常检查绑扎是否松动。

4.对学历的认同感主要是由于当前社会快速发展而带来的精英标准的上升，促使本科生做出考研的抉择。无论是由于“考研能提高自己的知识结构和层次”，还是“本科毕业已不具有竞争优势，硕士学位有利于将来更好的就业”，都反映了本科生考研行为是一种理性的抉择。

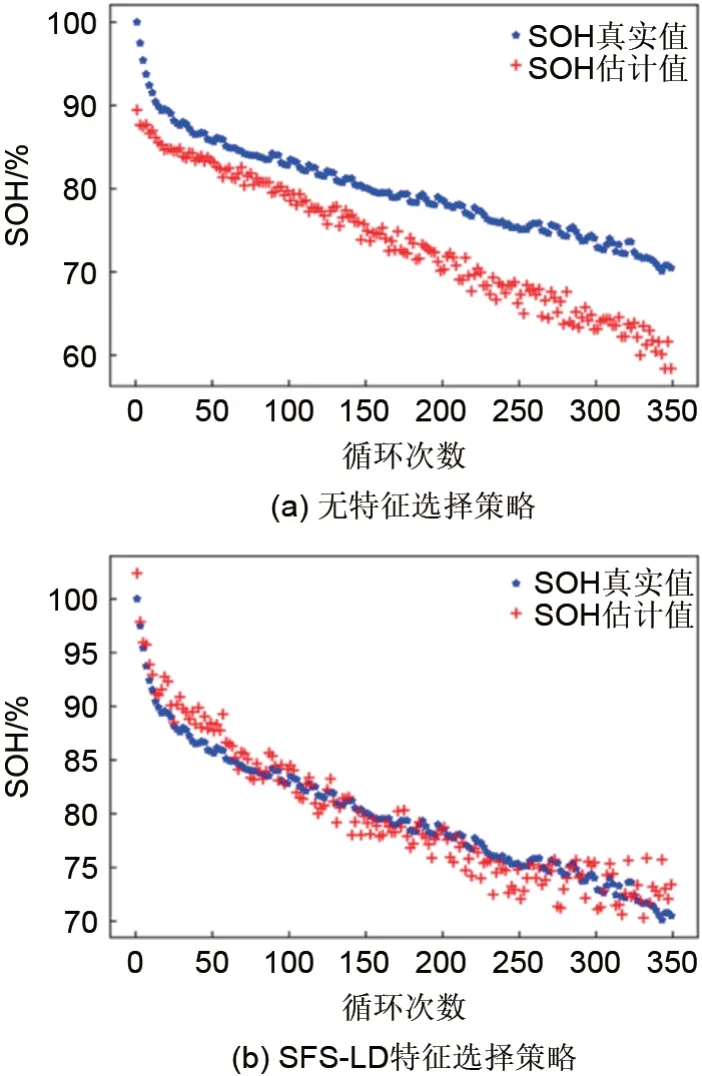
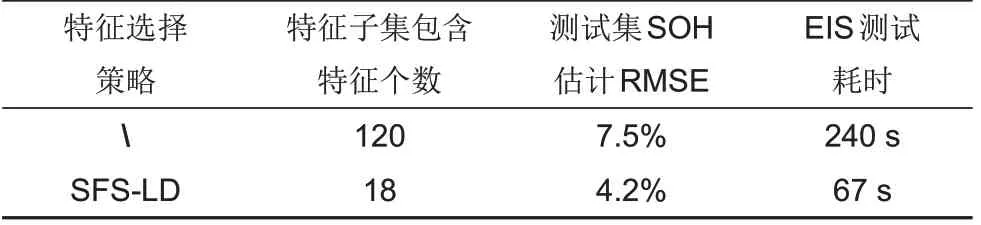
表1 从特征子集包含特征个数、测试集模型SOH估计精度以及EIS测试时间三个维度对比了无特征选择建模方法和基于SFS-LD策略建模方法的SOH估计性能。由表1可知，相较于直接将全频段EIS 数据作为输入变量的SOH 估计方法，基于SFS-LD 策略提前对全频段电化学阻抗特征集合进行优选，可得仅包含18 个阻抗特征的最优特征子集，特征个数显著降低，同时基于该特征子集构建的SOH 估计模型精度显著提高。此外，在测试时间方面，最优特征子集包含的频段EIS扫描测试仅需67 s，相较于全频段EIS 扫描测试耗时240 s，时间成本大为降低。上述结果表明，本研究提出的SFS-LD策略有效提升了模型的SOH估计精度，同时有助于降低SOH估计的测试成本。

2.3.2 模型估计精度与模型复杂度的均衡效果验证

为验证所提SFS-LD 策略在均衡模型估计精度与模型复杂度方面的有效性，本研究进一步对比了SFS 搜索中不同特征选择策略对SOH 估计模型的影响，具体结果如表2所示。其中，SFS-1表示仅优选1 个特征，SFS-2 表示优选包含2 个特征的特征子集，SFS-MIN 表示优选在训练集下交叉验证误差最小的特征子集，SFS-LD，即本文所提方法，表示优选特征子集综合性能评价指标最小的特征子集。

表2分别从特征子集包含特征个数、训练集及测试集模型SOH 估计误差对四种特征选择策略进行了比较。由表2 可知，随着优选特征个数的增加，训练集交叉验证RMSE 持续下降。当采用SFS-1 策略时，其训练集RMSE 最高，约为0.23%；当采用SFS-LD 策略时，其训练集RMSE约为0.03%，显著低于SFS-4 策略；当采用SFSMIN策略，其训练集RMSE与SFS-LD策略基本接近。从测试集SOH 估计结果可知，SFS-1 和SFS-4所得RMSE基本相同，接近6%；SFS-LD策略误差最小，仅为4.2%；SFS-MIN 策略误差为5.4%。上述结果表明，当优选特征子集包含特征数量较少时，例如仅优选1 个或4 个特征，虽然可有效降低模型运算复杂度，但是模型输入变量不足以充分表征SOH，导致SOH 估计误差偏大；当优选特征子集包含特征数量较多时，例如依照SFS-MIN 策略优选61 个特征作为模型输入变量，由于所选特征数量过多，未能有效剔除无关变量，同样导致SOH 估计误差偏大。相较而言，本研究所提SFSLD 策略能够筛选获得适量且有效的电化学阻抗特征，在降低模型运算复杂度的同时，实现高精度SOH估计。

3.2.3.2 选择合适静脉 下肢血栓的发生率是上肢的3倍［16］。所以避免在下肢建立静脉通路，特别是左下肢。在临床护理工作中，护理人员应提高静脉穿刺技能，避免在同一静脉处反复穿刺，穿刺部位若出现红肿等炎症反应和外渗，需立即更换穿刺部位，穿刺时尽量缩短扎止血带的时间，以减轻对血管的损伤。

3 结 论

为实现电池老化状态的快速、精准估计，本文从锂离子电池EIS数据出发，提出了一种结合SFS策略和LD方法的SOH估计模型。首先，通过SFS策略确定包含不同数量特征的阻抗特征子集；之后，以平衡模型复杂度与估计精度为目标，建立融合特征数量与交叉验证误差的综合性能评价指标，优选特征子集；最后，结合GPR 算法，构建SOH估计模型，实施老化状态估计。

所提方法采用公开发表的老化电化学阻抗数据集进行了验证。结果表明，引入所提SFS-LD特征选择策略后，SOH 建模所需阻抗特征数量显著减少，由120 个降低至18 个，电化学阻抗数据扫描耗时由240 s 降低至67 s，SOH 估计RMSE 从7.5%降低至4.2%。以上结果表明，所提SFS-LD策略能有效实施电池高维阻抗数据筛选，在大幅降低建模和测试成本的同时，实施锂离子电池精准SOH 估计，为电化学阻抗技术应用于SOH 在线估计提供理论和技术支撑。

[1] LU L G, HAN X B, LI J Q, et al. A review on the key issues for lithium-ion battery management in electric vehicles[J]. Journal of Power Sources,2013,226:272-288.

[2] HAN X B, LU L G, ZHENG Y J, et al.A review on the key issues of the lithium ion battery degradation among the whole life cycle[J].eTransportation,2019,1:100005.

[3] CHENG K W E, DIVAKAR B P, WU H J, et al. Batterymanagement system (BMS) and SOC development for electrical vehicles[J]. IEEE Transactions on Vehicular Technology, 2011,60(1):76-88.

[4] NG M F, ZHAO J, YAN Q Y, et al. Predicting the state of charge and health of batteries using data-driven machine learning[J].Nature Machine Intelligence,2020,2(3):161-170.

[5] ZHENG L F, ZHANG L, ZHU J G, et al. Co-estimation of state-ofcharge, capacity and resistance for lithium-ion batteries based on a high-fidelity electrochemical model[J]. Applied Energy, 2016,180:424-434.

[6] LAI X, ZHENG Y J, SUN T. A comparative study of different equivalent circuit models for estimating state-of-charge of lithiumion batteries[J].Electrochimica Acta,2018,259:566-577.

[7] KIM J, CHO B H. State-of-charge estimation and state-of-health prediction of a Li-ion degraded battery based on an EKF combined with a per-unit system[J]. IEEE Transactions on Vehicular Technology,2011,60(9):4249-4260.

[8] BI J, ZHANG T, YU H Y, et al. State-of-health estimation of lithium-ion battery packs in electric vehicles based on genetic resampling particle filter[J].Applied Energy,2016,182:558-568.

[9] SALKIND A J, FENNIE C, SINGH P, et al. Determination of stateof-charge and state-of-health of batteries by fuzzy logic methodology[J]. Journal of Power Sources, 1999, 80(1/2):293-300.

[10]ANDRE D, NUHIC A, SOCZKA-GUTH T, et al. Comparative study of a structured neural network and an extended Kalman filter for state of health determination of lithium-ion batteries in hybrid electricvehicles[J]. Engineering Applications of Artificial Intelligence,2013,26(3):951-961.

[11]HE Y J, SHEN J N, SHEN J F, et al. State of health estimation of lithium-ion batteries: A multiscale Gaussian process regression modeling approach[J].AIChE Journal,2015,61(5):1589-1600.

[12]庄全超,徐守冬,邱祥云,等.锂离子电池的电化学阻抗谱分析[J].化学进展,2010,22(6):1044-1057.ZHUANG Q C, XU S D, QIU X Y, et al. Diagnosis of electrochemical impedance spectroscopy in lithium ion batteries[J].Progress in Chemistry,2010,22(6):1044-1057.

[13]HUET F.A review of impedance measurements for determination of the state-of-charge or state-of-health of secondary batteries[J].Journal of Power Sources,1998,70(1):59-69.

[14]刘海洋. 基于阻抗谱时域测量的锂离子电池健康状态估计研究[D].哈尔滨:哈尔滨工业大学,2018.LIU H Y. Research on state of health estimation of lithium ion batteries based on time domian electrochemical impedance spectroscopy measurement[D]. Harbin: Harbin Institute of Technology,2018.

[15]STROE D I, SWIERCZYNSKI M, STAN A I, et al. Diagnosis of lithium-ion batteries state-of-health based on electrochemical impedance spectroscopy technique[C]//2014 IEEE Energy Conversion Congress and Exposition. September 14-18, 2014,Pittsburgh,PA,USA.IEEE,2014:4576-4582.

[16]GALEOTTI M, CINÀ L, GIAMMANCO C, et al. Performance analysis and SOH (state of health) evaluation of lithium polymer batteries through electrochemical impedance spectroscopy[J].Energy,2015,89:678-686.

[17]ZHU S, SUN X Y, GAO X Y, et al. Equivalent circuit model recognition of electrochemical impedance spectroscopy via machine learning[J]. Journal of Electroanalytical Chemistry, 2019,855:113627.

[18]ZHANG Y W,TANG Q C, ZHANG Y, et al. Identifying degradation patterns of lithium ion batteries from impedance spectroscopy using machine learning[J]. Nature Communications, 2020, 11:1706.

[19]UNGUREAN L, CÂRSTOIU G, MICEA M V, et al. Battery state of health estimation: A structured review of models, methods and commercial devices[J]. International Journal of Energy Research,2017,41(2):151-181.

[20]SUN Z H, BEBIS G, MILLER R. Object detection using feature subset selection[J]. Pattern Recognition, 2004, 37(11): 2165-2176.

[21]何志昆, 刘光斌, 赵曦晶, 等. 高斯过程回归方法综述[J]. 控制与决策,2013,28(8):1121-1129,1137.HE Z K,LIU G B,ZHAO X J,et al.Overview of Gaussian process regression[J]. Control and Decision, 2013, 28(8): 1121-1129,1137.

[22]BLASCO X, HERRERO J M, SANCHIS J, et al. A new graphical visualization of n-dimensional Pareto front for decision-making in multiobjective optimization[J]. Information Sciences, 2008, 178(20):3908-3924.

[23]MOMMA T, MATSUNAGA M, MUKOYAMA D, et al. Ac impedance analysis of lithium ion battery under temperature control[J].Journal of Power Sources,2012,216:304-307.