在数学教学中从代数出发理解函数

胡 乙

(江苏经贸职业技术学院 211168)

1 代数的产生及其功能

早期人们将数字与实际物品联系在一起，此时数与对象不可分割，人们不能从中提取数字.随着生产实践发展，人们对数的认识也逐渐深化，能从一支笔、一个人、一张纸中抽象出数字1，随着抽象思维的不断发展，人们尝试对数再次进行抽象，用代名词、文字、符号等代表任意数，例如用a代表1,2,3,…,等，研究文字或代名词算术的学问称为代数学.一般算术是一定的，具体的，而代数是不确定的、普遍的，为了深入研究生活中各种变化规律，人们在代数的基础上又发明了函数.由于代数能运用文字做帮手，故人们可用其表示算术法则、解方程、描述数学公式等.

1.1 代数与算术法则

以算术运算为例，其有一定的法则与规律，当描述加法交换律时，人们不能简单地归纳为2+3=3+2，因为这个叙述只是上述规律的一个特点.当人们要表示整数之间关系时，必须用文字来代替具体的数字，即用代名词来表示任意符合要求的数，这个代名词表示的数不是固定的，而是变化的，比如用a+b=b+a描述加法交换律，上述过程可称为算术的基本规律，其他算术基本规律也可用代数表示.有了算术规则，人们可以写出任意代数运算的表达式，简称代数式.最简单的代数式为单项式，比如axk.两个及以上的单项式组合为多项式，如x+1.略为复杂的多项式如x3+x2+1等，由于在计算中要弄清各个对象数量关系，人们逐渐用代数来探索方程的普遍的系统的解法.

1.2代数与解方程

数学中最基础的部分为算术，当人们发现算术中某些数量关系问题难以用普通算术方法解决，于是转而运用代数方法.王贵水指出：“用文字代表数的学问即为代数.为了寻找系统的、普遍的求解数量问题的解法，产生了以解方程为原理的初等代数.”代数与方程密不可分.用数字、文字或符号表示两个量相同的表达式称为等式，其描述了各个对象数量间的数量关系，含有未知数的等式就是方程.如果用文字表示未知数，人们把尚未知道的数用代数表示，运用移项或约同类项的复原方法来求解未知数，这是代数的优点，并且它可以解决原本用普通算术方法难以解决的问题.

1.3 代数与公式

公式是特殊的方程，它说明了各个对象之间的关系.例如，人们用代数描述正方形面积公式S=a2，a为边长.当a=1cm时，此时人们在代表一般数的代数中代入了特殊的数字.教师引导学生思考：如果将a与S视为两个口袋，当代入不同的a时，S数值有何变化？S与a是否对应？比如输入1个a，是否会出现2个S值？这里学生只要能判断两个口袋(集合)之间对应关系即可，教师运用数与代数知识，初步引导学生认识集合，为学生日后学习函数打下基础.

2 代数与函数的联系

随着生产发展与科学技术的进步，人们需要研究变化与运动的数学，比如为了计算太阳与月亮的运动轨迹，为了计算子弹、炮弹的弹道等，人们必须发明研究变化之术的学问，即函数.学生可将函数理解为描述变化和运动的数学语言.教师可与从代数式、代数方程、代数与数轴、代数变量等方面引导学生理解函数.

2.1 从代数式的结果出发理解函数

代数可代表变动的数，从代数式可初步理解函数的特点.假设存在代数式x2+1，且x的值不固定，则该代数式没有确定的数，学生可用x2+1=f(x)描述以上过程，以上代数式的值称为x的值的函数.R·柯朗与H·罗宾直接将代数式的不定结果视为函数，并提出不同量之间如果有物理关系则会出现函数概念，变量为集合中的一个元素.

最简单的函数为单项式函数，其表达式为f(x)=axk，a为任意实数，k是任意正整数，其也是单项式的次数.此类函数有f(x)=1，f(x)=-3x2等.

稍为复杂的为多项式函数，它是由两个或者两个以上单项式函数加在一起的和，如f(x)=1-3x2，其中单项式的最高次数代表该多项式的次数.

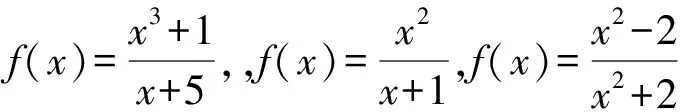
此外，还有自变量x以指数形式出现的指数函数以及三角函数等.

2.2 从代数解方程出发理解函数

代数能用字母表示未知数，从求解方程角度，教师可运用代数引导学生学习函数的作用.在早期解方程过程中，人们总是尝试代入特殊的数字进行求解，例如，欲求解x2+2x-1=0，则人们可以尝试代入两个特殊的值，使得代数式结果一个大于0，一个小于0.假设x=1，则x2+2x-1=2>0.假设x=0，则x2+2x-1=-1<0.故x的值应该位于0与1之间，取x=0.5，则x2+2x-1=0.25>0，故0与0.5之间，一定有某个值使得原代数式为0，后续计算以此类推，直到求出x为止.

在求解方程的过程中，人们每次都要写下诸如此类代数式，对于更为复杂的方程，如6x4-5x3+4x2+2x-1=0，如果每次都要完整写出此类代数式，则增加了负担、降低了效率.为提高效率，正如人们用乘法代替加法一样，在解方程中，人们可仿照代数用一个字母，比如y代表此类代数式，这种简化的代数形式即为函数.黄风义认为函数是代数的高级运算形式.对于x2+2x-1的结果，当用字母y来代表时，即y=x2+2x-1，该等式的含义是指，当x取某个数值，经过这个代数式运算后，得到y的相应数值.当x取不同数值，经过同样代数式计算后，得到的y一般也不同.为了体现x的值决定y的值，人们可以扩展字母的个数，附加其他字母来代表x决定y的这个事实.例如，对于y(x)=x2+2x-1，其清楚地表明x决定y，y依赖于x.用y(x)代表x2+2x-1，即令y(x)=x2+2x-1，总之，人们用一个字母或者符号代表某个运算表达式，简称函数.有时人们也可用f(x)来代表函数，其中字母f是函数单词(function)的首字母.

2.3 从代数与数轴出发理解函数

数、函数是数学的基本单元.在测量连续量与离散量时，为便于比较大小，笛卡尔创造性地将数以几何形式表示为直线数轴上的点，如此将难以直接比较的量转化为易于比较的量，通过比较数轴上的不同点与原点的距离，即可知道两个量的大小.数轴是以原点为中心，向两端无限延伸的直线.原点与0相对应，原点右边表示正数，其左边表示负数.人们可以将任意实数x描述为数轴上的点，可以在数轴上设定单位长度，这个点与原点的距离用设定的单位长度表示，即为实数x.如果x是一个固定实数，是具体的、个别的，则每个x都可以用数轴上某个确定的点表示，且数轴上每个点只能表示一个x.如果x是代数符号，是不确定的、普遍的数，则它是一个在数轴上不断移动的点，假设在数轴上存在多个不确定的代数移动点，要研究其中的数量关系，就需要用到函数.卡尔·P·西蒙等主张从代数与数轴出发理解函数，并视函数为数轴上实数的对应法则.

从代数与数轴考察，函数表示某一确定的对应规则，它使得对于数轴上的每个实数，都有函数确定的唯一的数轴上的实数与之对应.如果一个函数需要向任意一个实数x赋值，使得它所赋的值比实数x本身多2个单位，此时可将函数写成f(x)=x+2，该函数给2以4值，可以写成f(2)=4，同样，另一个函数使得它所赋的值是实数x本身，则可以写成g(x)=x，f(x)与g(x)表示不同的函数.

2.4 从代数变量出发理解函数

代数为函数的发展提供了有力工具.人们用代数x可表示直线上可以任意移动的点，因为此x表示变动的数量，故人们称为变量，变量的产生为函数的研究提供了方向和思路，人们可将函数视为描述变化和运动的数学语言.生活中的变量现象非常普遍，如果物体的面积与重量不断变化，则以上两个量即为变量.如果司机开车时不断调整速度，则速度值也是变量.此外，人的呼吸、脉搏随着情绪不断变化，家中的自来水表、煤气表随着能源的消耗亦是不断变化，以上皆为单个变量，单个变量只能孤立地描述事物的一个方面性质，为了应对生活中的复杂问题，为全面描述事物的状态，人们设想存在多个变量，力求从多个变量出发以更加全面地理解事物.正如医生看病时，不光要测量心跳，还要测量血压、体温，与仅仅测量心跳一个变量相比，以上该组变量一般能更为完整地描述病情.综上，从代数变量出发，教师可将函数解释为描述了各个变量间关系的数学语言.

除了单个变量外，两个变量间具有的关联变化是最简单的情形，即一个变量变动如何影响另一个变量值，学生对此也容易理解.例如商品价格对其销售量产生影响，货币投放量对本地区银行利率有影响，原料的投入对产品的产出有影响等等.为帮助学生理解，教师可运用生产机器的比喻来讲授函数.

整个函数如同一台用电脑程序控制的生产机器.假设有两个口袋A、B，电脑程序是某类代数运算法则，A口袋里装有原料，向机器投入原料后机器按电脑程序进行生产并产出产品，这些产品存入B口袋.假设电脑程序为投入1单位原料，可产生2单位的产品，以此类推，投入x单位原料，则可产生2x单位产品.假设这里只投入3次原料，A口袋中投入原料分别为1单位、2单位、3单位时，相应的则B口袋中产出分别为2单位、4单位、6单位.从函数考察：A口袋为限制输入量，它决定了B口袋的输出，电脑程序或者运算法则为f，用函数描述为：

f：A→B，f：x→2x

(1)

(1)表示：函数必有投入与产出，缺一不可.A口袋为投入，每一次投入必产生一个产品，这个产品存在于B口袋中.在具体的运算程序2x控制下，机器对x进行加工，产出产品值为2x.教师可用口袋比喻集合解释函数定义，如果A口袋中每一个投入物都能在B口袋中找到仅仅一个对应产出，则具体运算关系f就是函数.A口袋为定义口袋，B口袋为上域口袋，两个口袋间不同的对应关系决定了函数的类型.

总之，函数是代数式的不定结果，是高级的代数表达形式，表明了数轴上实数之间的对应关系，是描述各个变量间关系的数学语言.