稀释制冷机3 He-4 He 混合溶液非稳态制冷过程研究
2022-08-31郑茂文赵密广卫铃佼潘子杰梁惊涛陈厚磊
郑茂文 赵密广 卫铃佼 潘子杰 全 加 梁惊涛 陈厚磊
(1 中国科学院理化技术研究所,中国科学院空间功热转换技术重点实验室 北京 100190)
(2 中国科学院大学 北京 100049)
1 引 言
量子计算、深空探测、凝聚态物理是世界科学研究的前沿,更是国家科学技术发展的重要领域,具有重要的战略意义。这些研究工作的一个必要前提就是极低温环境。特别是量子计算领域,首先要解决的技术问题就是获得和保持100 mK 以下的极低温环境。目前能达到此温区的制冷技术主要是3He-4He 稀释制冷技术和磁制冷技术,而稀释制冷机则因其无磁场干扰、连续制冷、性能可靠稳定的优点成为量子计算等领域的主流极低温技术[1-2]。
自1965 年首次利用3He-4He 稀释制冷获得220 mK 的温度以来,国外针对各种流程的稀释制冷机进行了大量的研究工作[3-6],甚至应用到深空探测中[7-8]。目前商用稀释制冷机已经能实现10 mK 以下的最低温度,在100 mK 能提供1 mW 的制冷量。2016 年以前,由于中国在量子计算、极端物理等尖端领域的发展相对不足,对稀释制冷机的需求较少,国外的稀释制冷机产品完全能够满足需求。自1979 年冉启泽等研制出稀释制冷机[9]后,中国极低温的相关研究几乎处于空白。但近年来由于中国量子计算发展迅速,且其意义重大,欧美等国家针对量子计算的关键设备—稀释制冷机对中国进行了一定的限制,以此来遏制中国量子领域的发展。因此,中国国内部分单位开始稀释制冷机的研制工作。中国科学院物理研究所、中国科学院理化技术研究所和中船鹏力(超低温)科技有限公司等单位虽初步研制出样机,但针对稀释制冷的系统性研究较为缺乏,特别是针对非稳态制冷过程,国际上也研究较少。
本研究针对量子计算用基本型稀释制冷机,围绕其3He-4He 混合溶液的非稳态制冷过程展开研究。将非稳态降温过程分为减压制冷、经典态稀释、简并态稀释3 个阶段。首先对减压制冷阶段分析各参数对减压制冷的影响,得到温度、蒸气压、浓度等参数之间的对应关系。针对后两个阶段,主要推导相关临界点和不同状态的制冷效应,得到相分离的临界点和完全简并的临界温度。同时分析了非纯3He 循环、渗透阻力等非理想情况对制冷过程的影响。以上分析将有助于解稀释制冷机降温过程,特别是稀释制冷过程的启动和变化等相关过程的分析。
2 稀释制冷过程
2.1 稀释制冷原理
稀释制冷机是基于3He-4He 混合液的特性,利用3He 溶液向稀3He-4He 混合液中的稀释溶解,产生制冷效应。在饱和蒸气压下3He-4He 混合液相图如图1 所示,以温度约为0.87 K、67.5%的3He 浓度为起点,随着温度降低,3He-4He 混合液开始分为两相。这个点称为3He-4He 混合液的“三相点”,三相点下的曲线称为相分离曲线,相分离曲线中的阴影区域称为相分离区(两相区)。两相区,共存溶液分成两相,在重力场中,上层是富3He 的溶液(几乎是纯的3He),称为浓相;下层是稀3He 的溶液,称为稀相[10-11]。
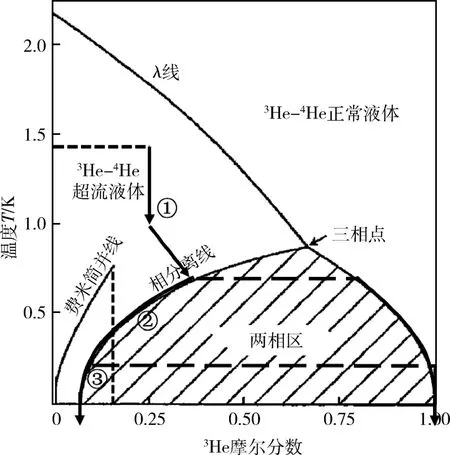
图1 3 He-4 He 混合液相图及非稳态降温过程Fig.1 Phase diagram and unsteady cooling process of3 He-4 He mixtures
2.2 稀释制冷循环
一般稀释制冷的基本原理如图2 所示,箭头方向代表工质(通常是3He)的循环方向。在稳态运行中,3He 气体首先在一二级预冷中被冷却,流阻前为1 K 液池或J-T 换热器,工质在此处冷凝为液体。流阻是为获得足够的凝聚压力和防止气体进入热交换器而设置的。流过流阻的液体依次经过蒸发器换热器、逆流热交换器到达混合室,在混合室中发生稀释制冷效应产生冷量后,沿相反方向穿过稳定的超流4He液柱进入蒸发器。3He 在蒸发器处由外部泵的作用蒸发分离进入下一循环。

图2 稀释制冷循环示意图Fig.2 Schematic diagram of dilution refrigeration cycle
在启动过程中,3He-4He 从外部经过预冷向稀释单元中冷凝,当冷凝完成气液界面到达蒸发器中合适位置,即可开始非稳态降温过程,直至降至最低温度到达稳态。
3 非稳态过程
将稀释制冷机启动中的非稳态降温过程分为3个阶段,如图1 中所示。3 个阶段分别表示:(1)第1个阶段是从减压阶段至相分离,此时混合溶液未产生相分离,混合溶液始终未达到饱和状态。图中直线表示等比例的混合气不断冷凝的过程,当冷凝完成开启减压后,蒸发器内的3He 蒸发向混合室聚集,使得混合室3He 浓度增加,将此阶段称为“未饱和减压制冷阶段”。(2)第2 个阶段是混合溶液产生相分离至转变为完全简并的费米液体,该过程中,蒸发器继续进行3He 减压蒸发,3He 不断向浓相侧富集,相分离界面逐渐从换热器向混合室移动,并到达混合室。温度持续下降,直至温度降至3He 费米简并转变,混合室稀释过程稳定发生,将此阶段称为“经典/弱简并稀释阶段”。(3)第3 阶段为“强简并稀释阶段”,指相分离后的稀相3He 浓度低于15%并逐步达到完全费米简并,产生稳定稀释制冷作用,直至稀释制冷作用最终达到稳态,进行完全简并的稳态运行。
3.1 减压制冷阶段
如图3 所示,在稀释制冷机的减压制冷过程中,蒸发器与混合室均为3He-4He 混合溶液,且理论上是近乎等温的,其减压的温度与蒸发器中3He 的含量有关。
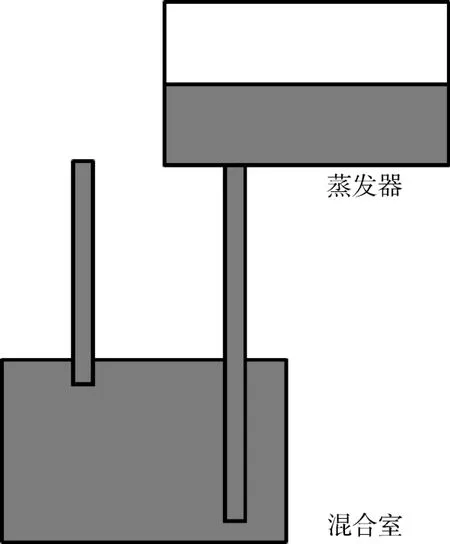
图3 减压阶段3 He-4 He 混合液示意图Fig.3 Schematic diagram of3 He-4 He mixture in decompression stage
蒸发制冷过程主要在蒸发器中产生,冷量由蒸发器中蒸发的工质气化潜热产生。蒸发器以下的液体理论上没有制冷效应,可将蒸发器及以下部分看作一个等温容积。设蒸发器和混合室这个总的等温容积内3He 的摩尔分数为x3,蒸发器内蒸发的工质流量为,蒸发器温度为Ts,经过流阻元件后进入蒸发器的液体工质的温度为T0。假设蒸发器中蒸发的气体为纯3He,当蒸发器通过减压达到一定的温度平衡时得到能量方程为:
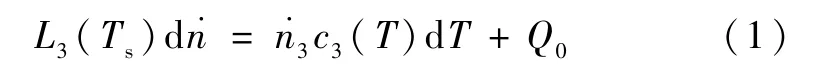
显然,蒸发器的状态由热负载和蒸发参数决定。当蒸发器没有额外的漏热,其主要热负载来自流阻后的工质。由于工质气液态的焓值差别较大,如图4 所示,1 K 以下工质气态的焓值远高于其液态焓值。若流阻未实现完全液化,将给蒸发器带来较大的热量。

图4 气液饱和态3 He 的焓值Fig.4 Enthalpy of3 He in gas-liquid saturated state
(1)热负载的影响
设经过流阻后的工质的干度为xg,那么蒸发器的守恒方程变为:
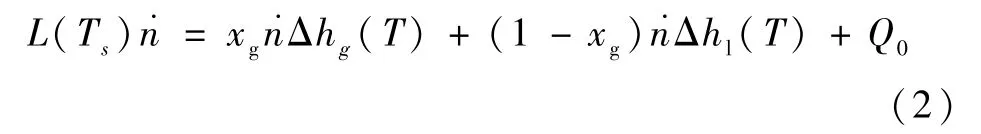
例如,在0.8 K 附近,汽化潜热为11 J/g,取系统原始漏热为1 mW,流阻后工质温度为2 K,那么得到干度与对应所需蒸发器的流量的关系如图4 -7 所示。可以看出,随着干度的增大,蒸发器所需流量显著增大。若从循环开始时,流阻后的工质一直未完全液化,会导致从一开始蒸发器的减压温度就无法降至合理区间,从而影响稀释和相分离的发生。

图5 流阻后工质干度对蒸发流量的影响Fig.5 Influence of working fluid dryness on flow rate after flow resistance
(2)蒸发参数的影响
纯的3He 和4He 的饱和蒸气压与温度相关=f(T),而对于二元混合液而言,其饱和蒸气压还与组分的含量有关,即Pv=但由于稀3He-4He混合溶液的特殊性质,关于3He 的分蒸气压要做一定修正,即稀3He-4He 混合溶液的蒸气压为:
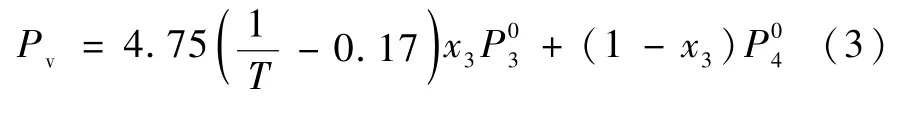
综上所述,在其他漏热可以忽略的情况下,流阻后工质的状态和蒸发器的背压、3He 摩尔分数决定了蒸发器的温度与流量。为了使蒸发器基础温度较低,应使流阻后工质尽量液化,同时蒸发器出口处泵的抽速要满足要求。至于蒸发器内的3He 摩尔分数则与渗透压平衡有关,在后文中分析。
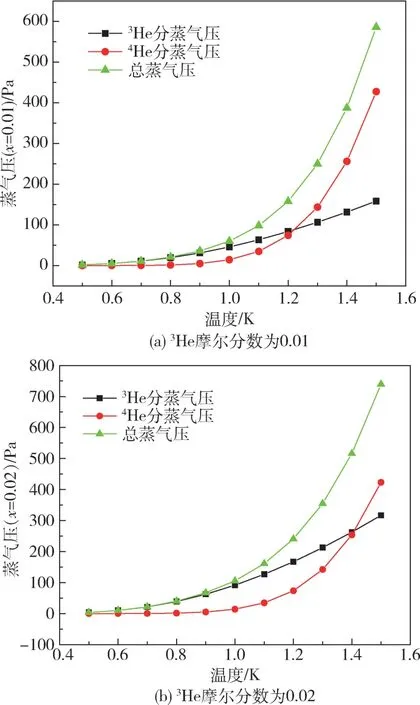
图6 不同3 He 摩尔分数下混合液的蒸气压Fig.6 Vapor pressure of mixed solutions at different3 He mole fractions
3.3 非稳态制冷
3.3.1 相分离的产生与费米转变
3He-4He 混合溶液降至0.87 K 后,虽然温度达到了三相点,但并不一定能产生相分离。根据前文的3He-4He 混合溶液相图(见图1),0.87 K 时对应的相分离线的3He 摩尔分数为0.67。为了找到相分离和稀释的临界条件,必须结合3He-4He 混合溶液的相图来进行分析。
相分离线左侧和右侧的饱和溶液曲线分别表示为[12-15]:x3D=0.064 8(1+8.4T2+9.4T3),x4C≡(1-x3C)=0.85T1.5exp(-0.56/T),该表达式只能作近似的估计,度越低其准确性越高。要发生相分离必须使得:
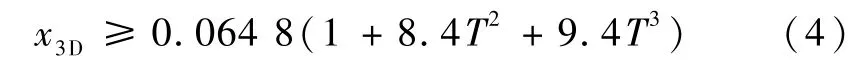
图1 中相分离线左侧上方单独的一条线即为费米简并温度曲线,可以看出费米简并转变温度曲线略高于相分离线。根据第二章中费米能的表述,可以得到费米简并温度的表达式
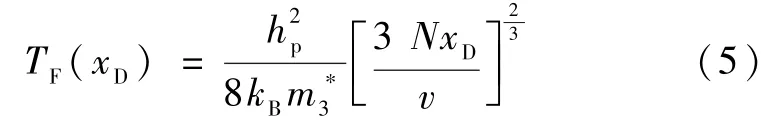
体积V中的费米子数服从量子统计学,根据相关代入结果有TF(xD)=。当T <TF(xD),3He分子开始从经典态转变为费米简并态,当T≤TF(xD)/3 则属于完全简并的费米态,而中间的温度则只能看作经典态和简并态的混合状态。联合以上各式,可以得到饱和态下的简并态转变普适温度为160 mK。
3.3.2 经典态稀释制冷
在0.87 K 以下,相分离产生前,入口的3He 在换热器中产生微弱的稀释制冷效应。随着温度不断下降,混合室达到相分离临界点,相分界面在混合室稳定存在,稀释制冷过程稳定发生,如图7 所示。稀释制冷基本方程可以表示为:

图7 相分离后的稀释单元Fig.7 Dilution unit after phase separation
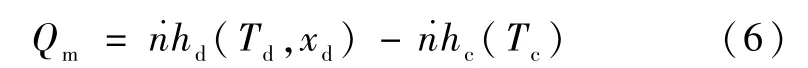
即制冷效应主要取决于稀相和浓相的焓差。
对于一个浓度为x的3He-4He 混合溶液,其比焓以每摩尔3He 为基本单位可以表示为:

可以得到:
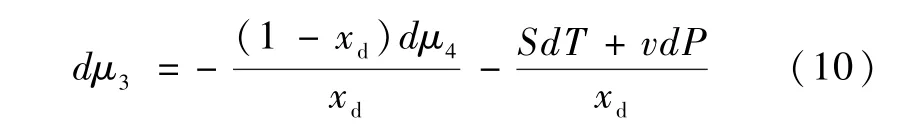
其中,由渗透压Π 的定义为:
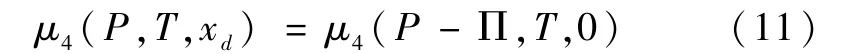
当压力趋近于0 时,忽略一般阻力,可以得到以下关系式:

根据热力学一般关系,代入式(10)得到:

可以得到任一混合溶液状态下的3He 化学势。在经典非稳态过程中,循环的气体为纯3He 时,其制冷方程简化表示为:
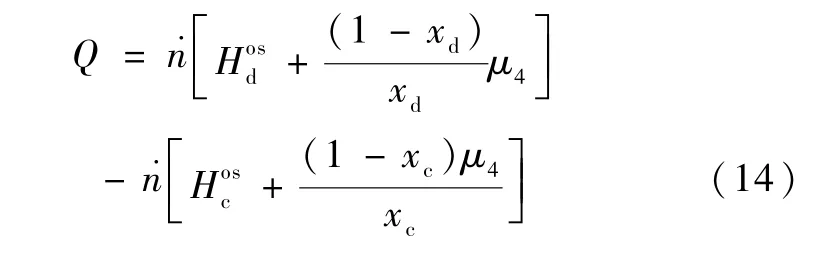
3.3.3 简并态稀释制冷
当经典态稀释过程发生,温度持续下降,直至T≤TF(xD)/3,混合室稀相可以看作完全简并的理想费米液体,4He 化学势守恒。稀相性质只与费米液体性质有关,即稀相焓为渗透焓。浓相和稀相的焓可以表示为:
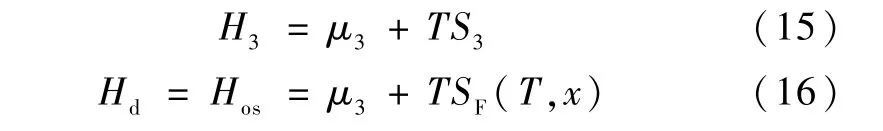
当且仅当3He 的化学势不变时,得制冷方程为:
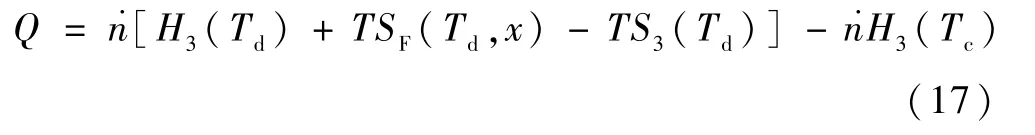
根据相关数据,近似取100 mK 以下c3=25T,c3D=107T,可以得到制冷表达式。与经典态相比,相当于少了4He 的化学势,同温度下简并态稀释的制冷效应增强。
根据以上分析,为了对比两种制冷情况,假设三相点以下全温区制冷方式相同,图8 给出了全温区理想费米液体的焓与经典液体的焓的比较。稀相与浓相之间的焓差即为制冷量,图中方形线为费米简并稀相焓,圆形线为费米简并浓相焓,上三角为经典稀相焓,下三角为经典浓相焓。实际过程中,在相分离前期,液体符合经典规律,制冷量为三角线之差。当温度持续下降,达到过渡范围时,液体逐渐转变为理想费米液体,则制冷过程逐渐过渡到制冷量较大的理想费米简并制冷区间,制冷量为方形线与圆形线之差。图中给出了当浓相、稀相温度相等时,即制冷量最大化的情况;图中同时给出了在浓相、稀相某温差下的制冷量三角形。可以看出,由于4He 化学势的影响,其制冷量相差较大。
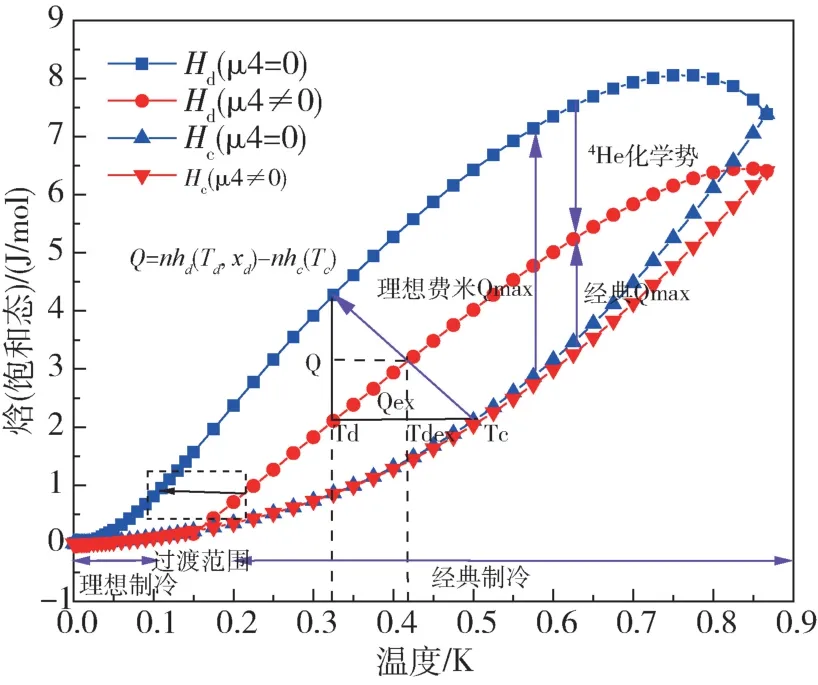
图8 完全简并渗透焓与经典焓的比较Fig.8 Comparison of fully degenerate permeation enthalpy and classical enthalpy
4 非理想因素分析
在整个稀释制冷循环中,始终存在非理想因素的影响。例如蒸发器中蒸发的工质总是含有少量的4He,而这会对稀释制冷过程产生影响。蒸发器的3He 摩尔分数则受渗透压平衡的影响,当3He 渗透阻力较大,会影响蒸发器的3He 含量,进而影响蒸发分离过程。
4.1 非纯3He 循环
进气不纯时,3He、4He 混合液体会在混合室入口处发生局部相分离,使进口成为3He 及部分3He-4He饱和溶液,更加恶化制冷性能,同时产生一定的析出热。设循环气中3He 的纯度为x,经推导可以得到制冷方程的化简表达式:
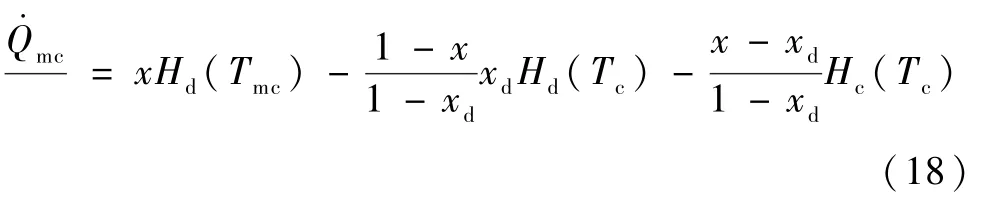
式(18)制冷方程右侧的2 项中,并不再是单纯的用稀相的焓减去浓相的焓,而是经过合并后的等效表达式.将第一项称为等效稀相焓Hd(eq),后两项之和称为等效入口焓Hc(eq)。
在稳态情况下,式(18)中的焓值均表示渗透焓。图9 给出了对于简并态稀释而言进气工质纯度对制冷性能的影响。可以看出,简并态制冷量只与总的进气3He 的量有关,其中循环的4He 不会对制冷过程造成本质性的影响。

图9 简并态下3 He 纯度对制冷性能的影响Fig.9 Influence of3 He purity on refrigeration performance in degenerate state
但是对经典液体而言,式(18)中的焓值均表示经典焓。图10 给出了经典态下进气工质纯度对制冷性能的影响。随着工质纯度的下降,其制冷性能逐渐恶化,更加不容易产生制冷效应,降温速度减小。当纯度仅50%,其制冷量极小,或许只能与相分离过程的析出热、漏热相平衡。在实验中发现,若启动过程中蒸发器维持着很高的温度,使得循环气体纯度较差,则很难通过稀释达到很低的温度。
4.2 非理想渗透
根据热力学一般关系的推导可以得到稀相中4He化学势的表达式为:
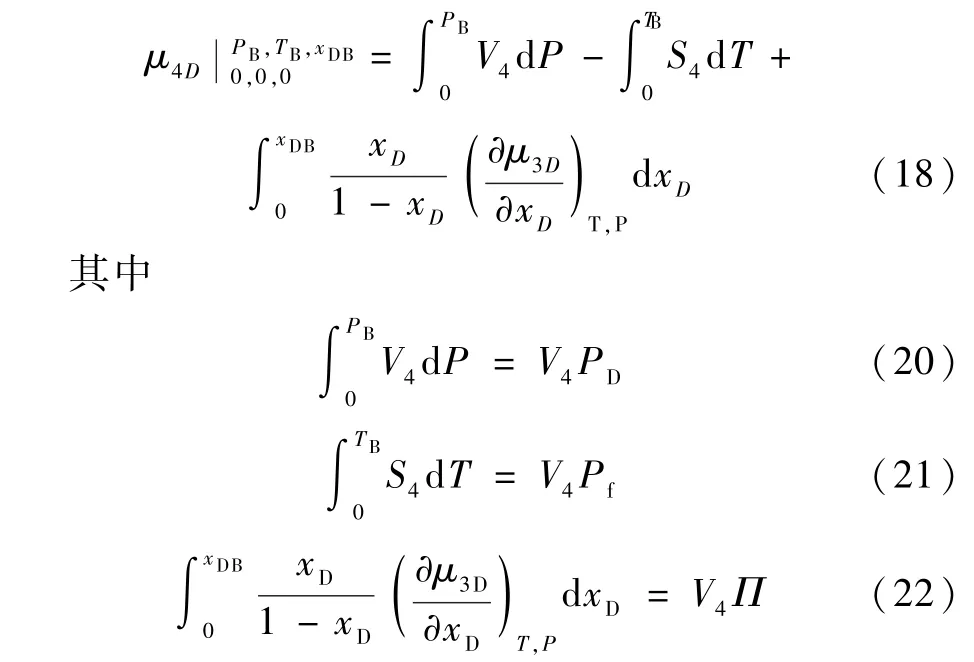
分别表示稀相的压力、4He 的喷泉压和渗透压。忽略前两项理想情况下可以得到经典态下渗透压表达式Π=
这对于蒸发器和经典态的混合室稀相是适用的。但对于费米简并态而言,渗透压为ΠF=
理想情况下,混合室与蒸发器之间没有阻力,渗透压平衡满足Πs=Πmc,即蒸发器的参数很大程度上由混合室决定。但在实际情况下,混合室与蒸发器间总是存在一个阻力。将式30-32 代入4He 的N-S方程,在无粘超流下可以得到:

即在维持化学势不变的趋势下,混合室与蒸发器间的渗透压差为ΔΠ=ΔPD。因此,为了保证混合室与蒸发器间有效渗透,应使得稀相管的阻力稍小。稀相管渗透阻力产生的压降关系可以表示为:
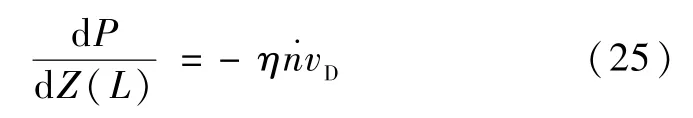
图11a 计算了不同浓度和温度下的渗透压计算值,计算中认为TF/3 温度以下的液体为理想费米液体,虚线表示文献中的测量值。而图11b 则给出了文献中经修正后的渗透压的值[12-15],其中虚线为理想费米行为液体的值。例如,对于0.064 浓度下的混合液,温度极低时的实际渗透压约为1.6 —2.0 kPa。

图11 不同浓度和温度下的渗透压Fig.11 Osmotic pressure at different concentrations and temperatures
图12 给出了0.1 K 下、3 m 长稀相管路,不同稀相管路水力直径和不同流量下的阻力压降。设计阻力压降至少维持在5 ×102Pa 以下。

图12 不同工况下的渗透压阻力压降ΔPFig.12 Pressure drop ΔP of osmotic resistance under different working conditions
在实验中,通过优化换热器稀相部分的渗透阻力,将纯干式稀释制冷机的蒸发器温度从1 K 下降至0.7 K 以下。
5 结 论
针对基本型稀释制冷机,围绕启动中的非稳态制冷过程,分析了减压制冷、经典态制冷和简并态制冷3 种情况下的制冷特性。结果显示,减压制冷过程中,蒸发器参数主要取决于漏热和蒸气压、浓度关系。经典态稀释制冷与简并态稀释制冷的制冷效应存在区别,而饱和态下二者的转变温度为160 mK 左右。
稀释制冷机中的非理想循环因素对制冷过程有一定影响。非纯3He 循环会极大弱化经典态制冷效应,但对简并态稀释制冷的影响较小(只取决于3He循环量)。混合室与蒸发器间的渗透阻力会影响蒸发器的浓度参数,从而影响循环流量和制冷效应。上述理论分析结果对稀释制冷机的研究和设计具有重要的指导意义,后续将通过实验优化,进行系统性的实验研究与理论计算进行比较完善。
