母函数非线性逼近的可解性*

潘云兰

(浙江师范大学 数学与计算机科学学院,浙江 金华 321004)

0 引 言

在一些数学和物理领域,常常需要研究如下形式级数的非线性逼近问题:

(1)

式(1)中: {fk}是一列数;{uk}是一列函数.部分作者用{uk}的母函数(参看定义1)作为研究工具,其早期工作可参阅文献[1-3]及其中的参考文献.

定义1设E是一元复函数空间,{uk}是E中的一列函数,{Hk[·]}是E上的一列线性算子.假定{uk}关于{Hk[·]}是标准正交的,即满足

Hk[um]=δmk,m,k= 0,1,2,….

其中,δmk是Kronecker函数.若

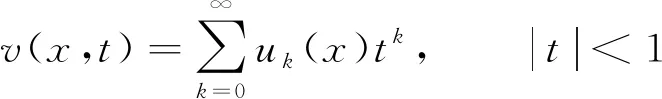
(2)

对每个|t|∈(0,1)都定义了E中的一个函数,则称v(x,t)为函数列{uk(x)}的母函数.

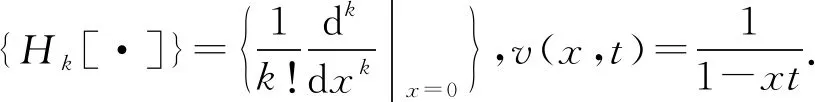
注1本文假定算子{Hk[·]}与求和符号之间满足如下的交换律:

注2对任一f∈E,记

fk=Hk[f],k= 0,1,2,…,

则有如下的形式展开:

(3)

式(3)中:aj和tj(j=1,2,…,n)满足

Hk[F(n;x)]=fk,k=0,1,…,2n-1.

(4)

把式(2)代入式(3),得

(5)

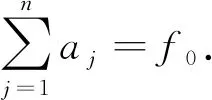
方程组(5)可用Prony方法[4]求解:先通过线性方程组

b0fk+b1fk+1+…+bn-1fk+n-1=-fk+n,k=0,1,…,n-1

(6)

求出b0,b1,…,bn-1;然后对多项式

p(t)=b0+b1t+…+bn-1tn-1+tn

(7)

求根得到t1,t2,…,tn;最后通过求解方程组(5)得到a1,a2,…,an.然而,Prony方法要求p(t)的根是单根.

Baker[1]讨论了0是重根的情形;Small[2]推广到所有tj都允许是重根的情形:设{rj}是根{tj}的重数,则式(3)中的逼近可以推广成以下形式：

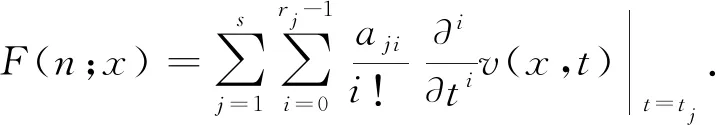
(8)

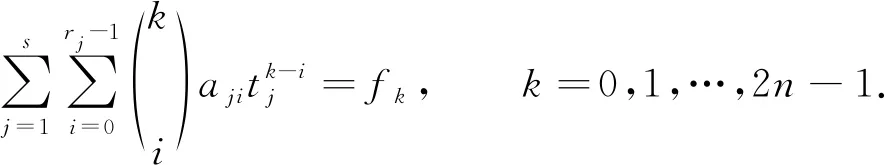
(9)

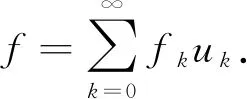
文献[5]给出了这种逼近的一些性质.文献[2]简述了用Prony方法求解方程组(9)的过程.即先从式(6)中求得{bj},然后求出式(7)中多项式p(t)的所有根及其相应的重数,最后通过解方程组(9)得到{aji}.

然而求得{tj}后,方程组(9)关于{aji}是个超定方程组,其可解性需要深入研究:什么条件下式(8)中的逼近F(n;x)存在?什么条件下它是唯一的?文献[6-11]对δ函数、δ函数的导函数及符号函数使用一些正交多项式的母函数进行了逼近,在这些特殊情形下回答了前述问题.但对一般情形至今还没有深入研究过.本文首先讨论良态问题(方程组(6)的系数矩阵非奇异),得到了逼近的存在性和唯一性;然后讨论病态问题(方程组(6)的系数矩阵奇异),通过修改式(2)中的母函数,在适当的条件下回答了上面的问题;最后给出了2个未解决的问题.

1 良态问题的可解性

接下来证明:给定正整数n,若问题是良态的,则由式(8)定义的逼近存在且唯一;当{tj}不含0时,式(8)中的{aji}可由方程组(9)中的任意n个相继的方程组成的方程组求出;当某个根tk=0时,{aji}可以由方程组(9)的最初rk个方程和其后的任意n-rk个相继的方程组成的方程组求出.

给定整数k(0≤k≤n),考虑方程组(9)中始于第k+1个方程的n个相继的方程组成的方程组,即

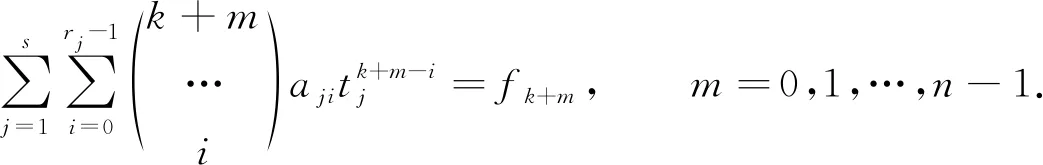
(10)

令B(k)表示其系数矩阵({aji}是未知量),则

引理1方程组(10)的系数矩阵B(k)的行列式的值是

证明给定整数k(0≤k≤n),引入关于变量x1,x2,…,xn的n×n阶修正Vandermonde矩阵

易知

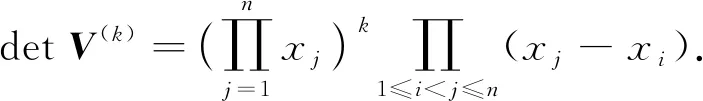
(11)

注意到B(k)可以由V(k)经如下的运算步骤得到:

分别对l=1,2,…,r1,用l!除以V(k)的第l列,然后对这一列求关于xl的l-1阶导数,最后令xl=t1;分别对l=1,2,…,r2,用l!除以V(k)的第r1+l列,然后对这一列求关于xr1+l的l-1阶导数,最后令xr1+l=t2;逐一对t3,t4,…,ts做类似运算.

受此启发,对式(11)做上述相同的除法、求导和代换可求得行列式detB(k)的值.具体步骤如下：

分别对l=1,2,…,r1,用l!除以式(11),然后求关于xl的l-1阶导数,最后令xl=t1.式(11)的右边成为

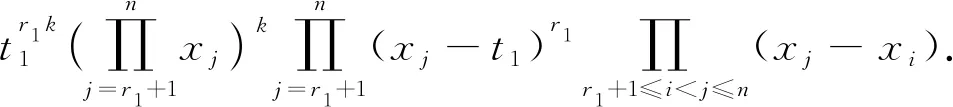
(12)

分别对l=1,2,…,r2,用l!除以式(12),然后求关于xr1+l的l-1阶导数,最后令xr1+l=t2,得

逐一对t3,t4,…,ts做类似运算.

一般地,在对t1,t2,…,tm做了这些运算之后,可以得到

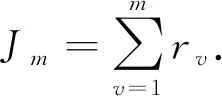
由引理1,易得以下推论:

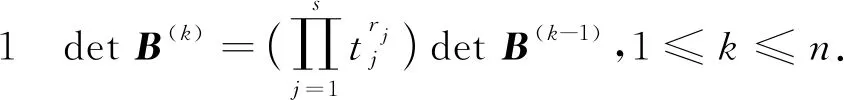
定理1回答了式(8)中线性参数{aji}的可解性.

定理1设b0,b1,…,bn-1是方程组(6)的解,t1,t2,…,ts是由式(7)定义的多项式p(t)的两两不同的根,{rj}是{tj}的重数.则:

1)当{tj}不含0时,式(8)中的{aji}可由方程组(9)中的任意n个相继的方程组成的方程组唯一确定;

2)当某个根tk=0时,{aji}可以由方程组(9)中的前rk个方程和其后的任意n-rk个相继的方程组成的方程组唯一确定.

证明1)注意到方程组(10)是由方程组(9)中始于第k+1个方程的n个相继的方程组成的方程组,B(k)是其系数矩阵.当{tj}不含0时,由引理1即得detB(k)≠0.由Cramer法则得方程组(10)的解为

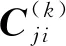
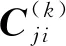
其中,当l=j时,q≠i.由式(6)得

对每对q和l(q=0,1,…,rl-1,l=1,2,…,s,且当l=j时,q≠i),因为

所以

或等价地,

(13)

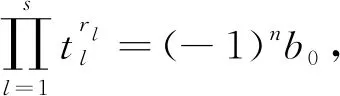
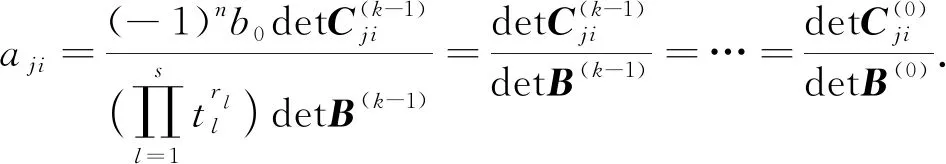
(14)

因为式(14)对i=0,1,…,rj-1,j=1,2,…,s都成立，所以1)成立.

2)不失一般性,假定ts=0.则式(7)中的多项式成为

p(t)=tn+bn-1tn-1+…+brstrs,brs≠0.

即b0=b1=…=brs-1=0.

用方程组(9)的最初rs个方程和其后的任意n-rs个相继的方程组成如下方程组:

其中,rs≤k≤n+rs.

用brs,brs+1,…,bn-1对后面的n-rs个方程实施类似于1)中的证明,可求出aji(i=0,1,…,rj-1,j=1,2,…,s-1),且其结果不依赖于这n-rs个相继方程的选择.显然,在求出这几个aji后,剩下的as1,as2,…,asrs-1可由前面的rs个方程唯一确定.定理1证毕.

由定理1即可得到存在性和唯一性定理.

定理2给定正整数n,令Δ(n)表示方程组(6)的系数矩阵行列式,如果Δ(n)≠0,那么定义2中的非线性逼近F(n;x)存在且唯一.

证明如果Δ(n)≠0,那么方程组(6)中的未知量{bm}可以唯一确定,从而F(n;x)中的非线性参数{tj}可以由式(7)唯一确定.所以由定理1,F(n;x)中的线性参数{aji}可以由方程组(9)唯一确定.定理2证毕.

2 病态问题的可解性

在实际中,我们要处理的问题常常是病态的.例如,当级数(1)中的{uk(x)}是正交多项式时,uk(x)在k是偶数时是偶函数;在k是奇数时是奇函数.此时,只有偶数(或奇数)下标的fk不为0.故有时方程组(6)的系数矩阵行列式形如

由于其奇数行线性相关,所以Δ(n)=0.这意味着方程组(6)无法确定{bm},从而导致F(n;x)中的非线性参数{tj}也无法确定.

然而,对一般情形解决这样的病态问题是件非常困难的事情,所以可以假定

uk(-x)=(-1)kuk(x),k=0,1,2,…,且当k是偶数时,fk=0.

(15)

主要策略是修改式(2)中的母函数v(x,t)以便达到Δ(n)≠0.

策略1对任一由式(2)给定的母函数v(x,t),记

由定义2知,F1(n;x)具有形式

类似于式(9),{aji}和{tj}的匹配条件成为

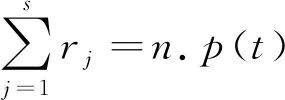
b0fk+b1fk+1+…+bn-1fk+n-1=-fk+n,k=1,2,…,n.

(16)

记

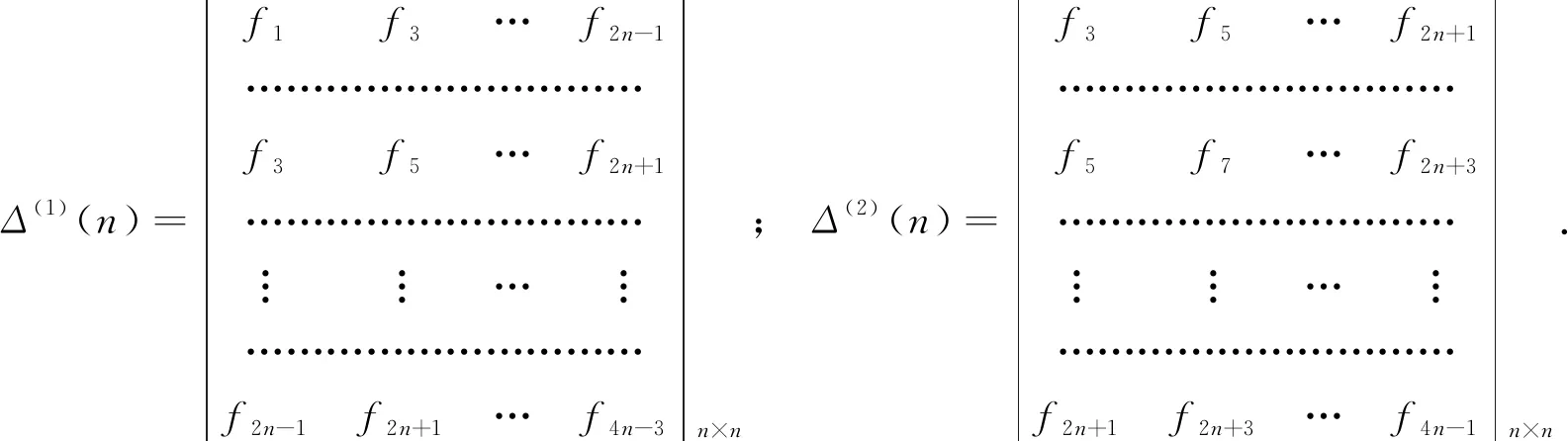
(17)

先给出存在性和唯一性定理.

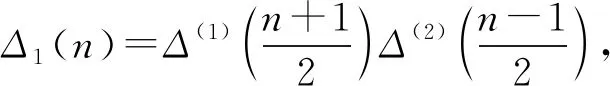
分别表示f(x)关于v1(x,t)和v(x,t)的2n阶逼近.因此,如果Δ(1)(n)≠0,Δ(2)(n)≠0,那么

s=S,Rj=rj,Tj=tj,j=1,2,…,s.

(18)

进一步,如果所有{tj}都是单根,那么

F1(2n;x)=F(2n;x),Aj=tjaj,j=1,2,…,2n.

其中,{Aj}和{aj}分别表示{Aj 0}和{aj 0}.

证明假定{Tj}和{tj}分别是

的两两不同的根.其中,P(T)和p(t)的系数分别由下列2个方程组确定:

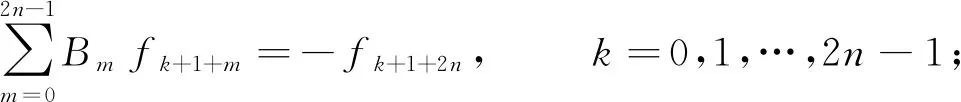
(19)

(20)

因为f2k=0,k=0,1,2,…,所以方程组(19)等价于下列2个方程组:

(21)

(22)

而方程组(20)等价于:

(23)

(24)

由Δ(2)(n)≠0知方程组(21)有唯一解B2m+1=0,m=0,1,…,n-1;由Δ(1)(n)≠0知方程组(23)有唯一解b2m+1=0,m=0,1,…,n-1.注意到方程组(22)和方程组(24)同解,故由Δ(1)(n)≠0知,

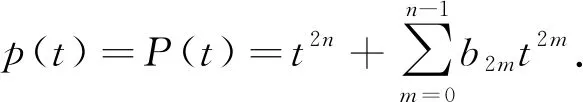
(25)

即式(18)成立.

下证定理的剩余部分.由式(18)知,Tj=tj,j=1,2,…,2n.从而关于F1(2n;x)和F(2n;x)的匹配条件成为:

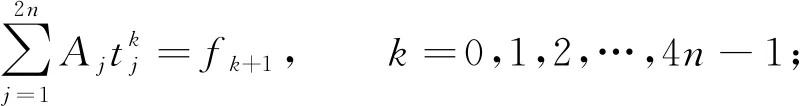
(26)

(27)

若所有{tj}都是单根,则它们非0.事实上,若有根为0,则式(25)中的多项式p(t)没有常数项,即0至少是2重根,矛盾.

由定理1知,{Aj}和{aj}可以分别从方程组(26)和方程组(27)的任意2n个相继方程中解得.考虑方程组(27)的如下2n个相继方程:

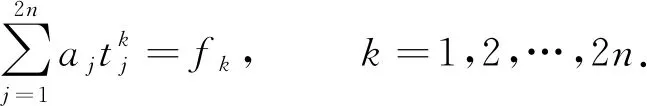
(28)

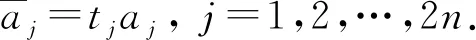
这和由方程组(26)的最初2n个相继方程组成的方程组同解.由此得:Aj=tjaj,j=1,2,…,2n.

定理4证毕.

策略2对任一由式(2)给定的母函数v(x,t),设uk(-x)=(-1)kuk(x),k=0,1,2,….记

由定义2知,Fo(n;x)具有形式

类似于式(9),{Aji}和{Tj}的匹配条件成为

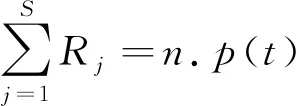
b0f2k+1+b1f2k+3+…+bn-1f2k+2n-1=-f2k+2n+1,k=0,1,…,n-1.

(29)

注意到由式(17)定义的Δ(1)(n)即为方程组(29)的系数矩阵行列式,类似于定理2的证明即可得Fo(n;x)的存在性和唯一性定理.

定理5给定正整数n,如果Δ(1)(n)≠0,那么Fo(n;x)存在且唯一.

下面定理说明,在适当条件下,Fo(n;x)和关于v(x,t)的逼近F(2n;x)相同.

分别是f(x)的关于vo(x,t)的n阶和关于v(x,t)的2n阶逼近.如果Δ(1)(n)≠0,那么下列结论成立:

1)若每个Tj都非0,则

2)若每个Tj都是非0的单根,则

3)若T1=0有重数R1,且其他{Tj}都是单根,则

Fo(n;x)=F(2n;x),r1=2R1,s=2S-1;

a1(2i)=0,a1(2i+1)=A1i,i=0,1, …,R1-1;

证明1)设{Tj}和{tj}分别是下面2个多项式的两两不同的根：

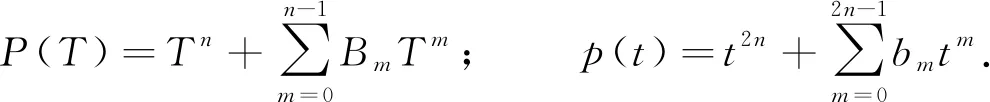
(30)

类似于定理4的证明可得b2m=Bm,b2m+1=0,m=0,1,…,n-1.故

(31)

通过对根进行适当排序,即得

由于Tj≠0,j=1,2,…,S,因此,s=2S.

2)由1)可知,所有的tj非0且单,因此{Aji}和{aji}中的下标i总是0,且S=n,s=2n.为方便起见,分别用{Aj}和{aj}表示{Aj 0}和{aj 0}.求出{Tj}后,由定理1知,{Aj}和{aj}分别由

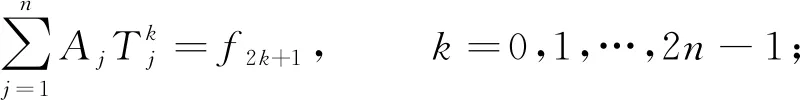
(32)

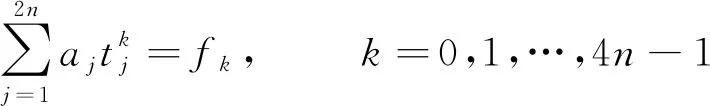
(33)

唯一确定.

设{Aj}是方程组(33)的解,下证

是方程组(33)的解.事实上,对m=0,1,2,…,2n-1,由1)即得

下证F(2n;x)=Fo(n;x).

3)由式(30)和式(31)得,r1=2R1且s=2S-1.故{Aji}和{aji}分别由

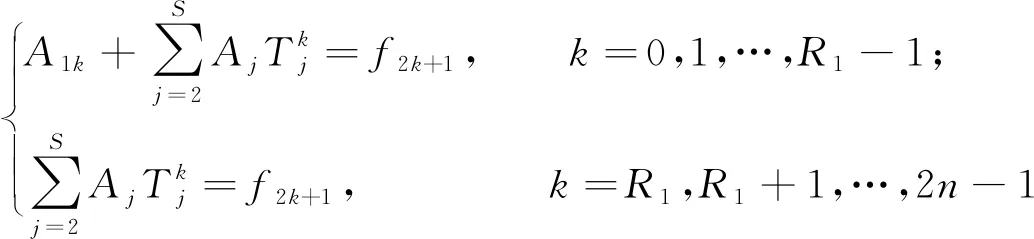
(34)

和

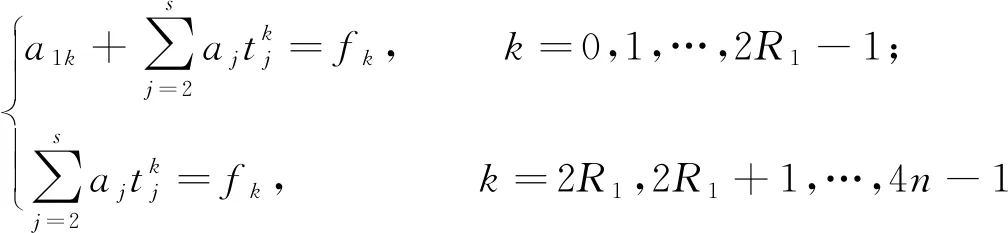
(35)

定理6证毕.

注意到Fo(n;x)涉及的参数比F(2n;x)少,故Fo(n;x)需要的计算资源比F(2n;x)需要的计算资源更少,因此,使用Fo(n;x)比使用F(2n;x)更有效.

3 结 语

本文研究了由式(8)定义且满足式(9)的母函数非线性逼近的可解性,分别在良态和病态情形下得到了一些解法.不过如下2个问题还未解决,值得继续深入研究:

1)当{tj}含有重根时,定理4中的F1(2n;x)=F(2n;x)是否还成立?

2)当{tj}含有非0重根时,定理6中的结论是否还成立?