驱油用聚合物溶液的流变模型应用优化研究
2022-08-31朱诗杰叶仲斌施雷庭徐建根刘哲知
朱诗杰,叶仲斌,施雷庭,宋 瑞,4,徐建根,刘哲知
(1.重庆科技学院石油与天然气工程学院,重庆401331;2.成都工业学院,四川成都611730;3.西南石油大学油气藏地质与开发工程国家重点实验室,四川成都610500;4.中海油能源发展股份有限公司工程技术分公司,天津300452)
驱油用聚合物溶液的完整剪切流变曲线特征应该包括零剪切段、假塑段、极限剪切段、黏弹段、降解段5 个部分(图1a)[1-2]:假塑段是驱油用聚合物最为常见的“剪切变稀”特征段[3-5];零剪切段是指在很小的剪切速率下,流动对分子结构无影响,聚合物溶液黏度不随剪切速率变化而变化,即牛顿段,此时测定的黏度就是零剪切黏度,对应的剪切速率就是零剪切速率[6-8];极限剪切段是因为剪切速率增加到一定程度后,大分子取向达到极限状态,取向程度不再随剪切速率变化而变化,聚合物溶液遵守牛顿流动定律,表观黏度又成为常数,这就是极限牛顿段[9-11];流变仪的测定中,极限牛顿段这个区域也是能够获取的,虽然黏弹段和降解段在常规研究中较为少见,但是依然有相关文献证实了其存在。
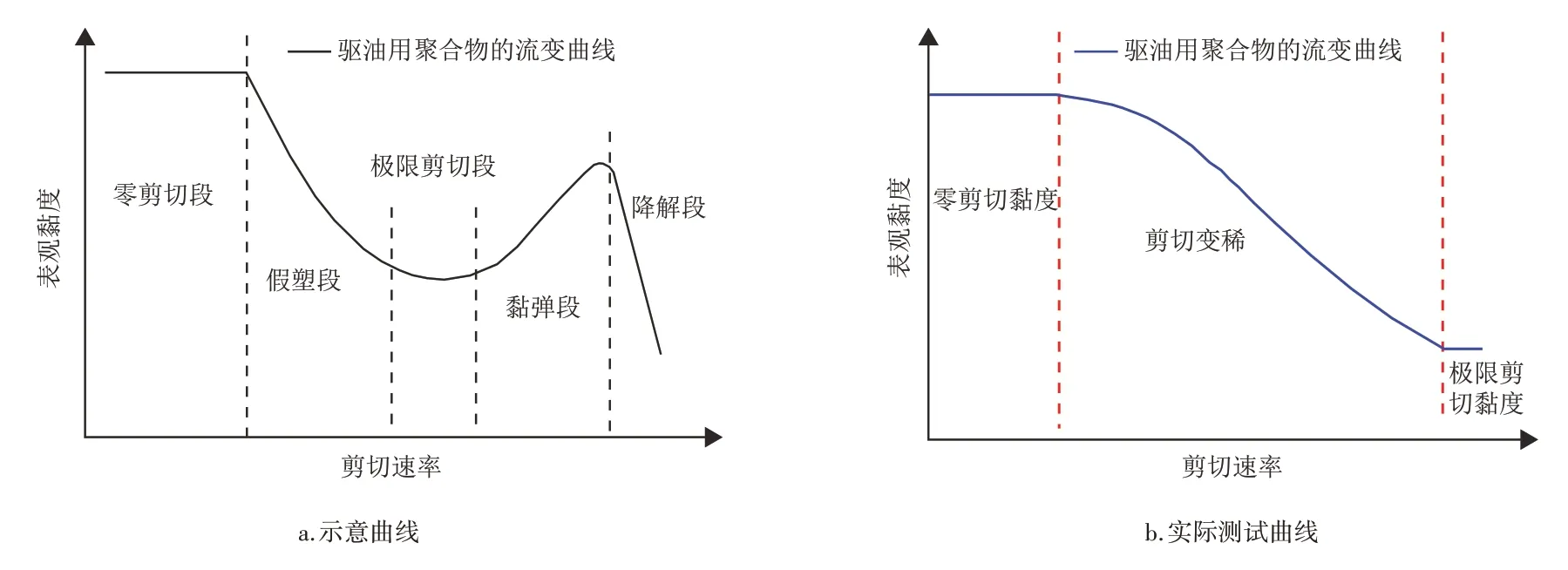
图1 驱油用聚合物的剪切流变特征Fig.1 Shear rheological characteristics of polymer for oil displacement
综上所述,采用可以表征零剪切黏度段、剪切变稀段、极限剪切黏度段3 个部分的数学模型(图1b),是目前描述驱油用聚合物流变性最为完整的,主要有Cross 模型和Carreau 模型[12-13]。对比两个公式,Carreau模型是驱油用聚合物较为适宜的表征模型[14]。
目前对于本构方程的拟合应用存在一个明显的问题,就是采用最小二乘法的非线性拟合过程中所得的数据与实际数据之间误差的平方和为最小,求取的未知参数组合数据较多,没有限定条件的特征松弛时间在拟合结果参数中数值波动较大,难以表征出黏弹性流体的弹性特征,特别是拟合不同聚合物溶液质量分数时的流变曲线,表征溶液特征参数值的准确度较低。因此,有必要建立一种解析驱油用聚合物流变模型的方法,提高其数值模拟的准确度。针对两种成熟工业化应用的聚合物溶液部分水解聚丙烯酰胺(HPAM)和疏水缔合聚合物(HAWP)开展室内实验获得溶液的流变性和黏弹性,以Carreau 模型为基础,通过应用黏弹模量实验数据,建立聚合物溶液的特征松弛时间约束条件,进行非线性回归不同质量分数的聚合物流变曲线,建立具有规律梯度的特征参数,确保拟合的准确度。
1 实验和理论基础
1.1 实验条件
实验用聚合物[15-16]:部分水解聚丙烯酰胺(HPAM),黏均分子量2 000×104,固含量88.9%,特性黏数1 855.7 mL/g,水解度26%,大庆炼化公司生产,分子式见图2a。疏水缔合聚合物(HAWP),黏均分子量1 800×104,固含量88.0%,特性黏数2 447.0 mL/g,水解度23.6%,四川光亚公司生产,分子式见图2b。

图2 聚合物的分子式Fig.2 Molecular formula of polymer
实验盐水:3 000 mg/L 的氯化钠,模拟溶液中的阳离子对聚合物溶液的影响;实验仪器:RS600 哈克旋转流变仪,机械搅拌器,1 000 mL 容量瓶,0.1%精度的电子天平,干燥皿;实验温度:20 ℃;溶液的流变性测定[17]:配制两种聚合物溶液,质量分数分别为0.10 %,0.14 %,0.20 %,0.25 %,设置剪切速率从r′=0.01 s-1到r′=10 000 s-1。
溶液的黏弹性的测定[18]:对两种聚合物溶液进行溶液配制,质量分数分别为0.10 %,0.14 %,0.20 %,0.25 %,设置角频率从10 rad/s 到0.01 rad/s,步长设置为4。
1.2 数学分析理论
1.2.1 松弛时间谱的计算
松弛时间谱是描述材料黏弹性对时间或频率依赖关系最一般的函数关系,流体的全部特性都表现在松弛时间各不相同的所有运动模式和的贡献中[19]。通过黏弹性模量的测试数据,应用典型线性本构方程(Maxwell 模型)分析线性黏弹性区间数据,聚合物熔体的储能模量和耗能模量可表示成离散形式,根据实验所测得的不同频率ωj下的G′、G″,采用最小二乘法,添加约束条件,λi和gi大于0,计算方法全局最优,计算出材料的离散松弛时间谱(λi,gi)[20-21]。松弛时间谱是松弛时间和模量的函数关系式:

式中:ωj为剪切振荡频率,Hz;j为实验频率节点;N为不同的Maxwell 运动单元数目,采用六参数的计算最为准确[22],N组(λi,gi)构成材料的离散松弛时间谱。
1.2.2 动态模量的计算
根据聚合物G′、G″可以求取动态模量G*,见式(3)[23]。动态模量是表征材料在不同的外载作用下不同的响应特性,由于相位差的存在,产生了滞后现象,使得应变分成了两部分,第一部分为弹性贡献,与应变呈线性关系,第二部分为黏性贡献,与应变速率呈线性关系:

式中:G*为动态模量,Pa;G′为弹性模量,Pa;G″为黏性模量,Pa;i为相位角,°。
将线性黏弹性材料的总应力用广义Maxwell 模型表示并对应变微分[8],采用傅里叶变换求解微分方程,可得动态模量表达式:

松弛模量表示的是材料的松弛性能,是在一定的温度和应力条件下材料应力与应变的比值。采用广义Maxwell 模型可以建立松弛模量与动态模量的关系式:

式中:g(i)为弹性模量与黏性模量组合的动态模量值;t为时间变量,s。
1.2.3 非线性回归流变曲线
应用MATLAB 软件,将流变实验数据带入Carreau-Yasuda 模型式(6)进行拟合,获取表征流变的特征参数:

式中:μ为表观黏度,mPa·s;μ0为零剪切黏度,mPa·s;μinf为极限剪切黏度,mPa·s;λ为特征松弛时间,s;x为剪切速率,s-1;n为Carreau指数;a为Carreau常数。
2 结果与分析
2.1 驱油用聚合物溶液的黏弹特性
2.1.1 动态振荡实验数据
两种聚合物溶液符合线性黏弹性区间的频率为0.1~1.7 Hz。因此,部分水解聚丙烯酰胺(HPAM)和疏水缔合聚合物AP-P4 溶液在线性黏弹区间内的黏弹性实验数据结果见图3、图4。

图3 HPAM的弹性模量和黏性模量Fig.3 Elastic modulus and viscosity modulus of HPAM

图4 AP-P4的弹性模量和黏性模量Fig.4 Elastic modulus and viscosity modulus of polymer AP-P4
部分水解聚丙烯酰胺(HPAM)在不同质量分数条件下的储能/耗能模量存在一定的差异:①质量分数为0.10%和0.14%的耗能模量G″在整个振荡频率范围内占据主导地位,表现出较强的黏性特征;②质量分数增大至0.20%以后,在低振荡频率范围内,耗能模量占据主导地位,随着振荡频率的增加,储能模量增幅更强,逐渐占据主导地位,质量分数为0.25%时,该现象更为明显。这就说明,HPAM 在较高质量分数下,同时振荡频率较好的条件下,其弹性特征的表现才会更加的明显。在其黏弹性的表征中主要是以黏性特征为主导作用,包括其在多孔介质中的流动时,如果不能产生较强的弹性形变特征,整个流动阻力的建立应该是以黏性黏度作为主导。
对于疏水缔合聚合物AP-P4(图4),低于临界缔合质量分数的黏弹性特征(临界缔合质量分数为0.14%)出现了G′和G″的交点;高于临界缔合质量分数的3个溶液质量分数,均表现出储能模量强于耗能模量,这表明在研究的振荡区间内,聚合物AP-P4 的黏弹性是以弹性为主的变化特征,弹性特征占据主导地位。相比HPAM,高质量分数条件下AP-P4 的弹性模量和储能模量均远大于同质量分数条件下的HPAM,这说明缔合作用明显增强了聚合物分子间的作用力,又特别表现在增加了弹性模量特征。临界缔合质量分数之下,AP-P4 依然是以弹性模量占据主导,这是因为分子内缔合加强了聚合物的内聚力,使其抗形变能力大增。
可以看出,AP-P4 的黏性特征变化中,弹性模量十分重要,研究过程中不可忽视弹性作用带来的影响,在后续的研究中应该考虑弹性模量的影响。
2.1.2 松弛时间的特征参数限定优化
1)HPAM、AP-P4 的动态模量数据见表1。表1中的HPAM 和AP-P4 都是随着溶液质量分数增加,振荡频率增加,动态模量呈现上升趋势。根据其拟合的幂律公式,计算可得研究质量分数范围内的两种聚合物HPAM 和AP-P4,溶液G*变化分别为0.01~1.00 Pa 和0.15~2.00 Pa。其中,AP-P4 动态模量表现出的上升趋势规律性没有HPAM 强,临界缔合质量分数(0.14%)以下的0.10%规律不同于临界缔合质量分数以上的规律特征,这是聚合物的缔合作用对其复数模量特征的影响。质量分数0.25%的AP-P4 在0.1 Hz 下的复数模量超过1 Pa,相较于HPAM,其具备更强的模量特征。

表1 不同质量分数下聚合物的动态模量Table 1 Dynamic modulus of polymer at different concentrations
2)HPAM 和AP-P4 的松弛时间谱见表2。部分水解聚丙烯酰胺(HPAM)的松弛时间谱具有较为明显的规律,随着松弛时间的增加,松弛模量呈现下降的趋势,达到100 s 时,松弛模量呈现数量级的下降;而随着聚合物溶液质量分数的增加,均呈现出类似的特征。分析认为这是线性聚合物HPAM 的分子结构特征决定的,其聚集行为是呈现“颗粒”堆积的现象,溶液质量分数的增加使其聚集行为增大,堆积体变大,但并没有改变本质的分子间作用力,所以其具有较为明显的规律性[24]。AP-P4 的松弛时间谱呈现的特征明显区别于HPAM,不再存在明显的松弛模量随着松弛时间增加而下降的规律性。通过表2 可以归纳为:①在低松弛时间条件下,保持较高的模量特征;②在较高松弛时间下依然具备一定的模量值,说明其弹性能量较大;③与HPAM 对比,AP-P4 具有更大的松弛时间数学变量。缔合作用增强的弹性模量和黏性模量很好地表现在了松弛时间谱上。

表2 两种聚合物的松弛谱特征Table 2 Relaxation spectrum characteristics of two polymers
通过松弛模量与动态模量的公式转化,利用实验数据计算的动态模量范围限制即可获得两种聚合物在实验条件下的松弛时间范围(表3)。

表3 研究质量分数范围内的聚合物松弛时间范围Table 3 Polymer relaxation time range in study concentration range
2.2 驱油用聚合物溶液的流变特性
2.2.1 聚合物的流变曲线特征
HPAM 和AP-P4 的流变曲线实验结果见图5 和图6。从图5 可以看出,当剪切速率为2 500 s-1左右时,不同质量分数条件下HPAM 的流变作用特征均发生变化,这表明聚合物溶液达到了临界剪切速率,而且HPAM 的临界剪切速率范围并没有受到溶液质量分数的影响,4个溶液质量分数条件下都是该剪切速率下出现黏度大幅度下降的特征。但是不同质量分数聚合物在超过临界剪切速率的流变表现不一样,溶液质量分数较高的0.20%、0.25%在当前条件下溶液黏度直线下降;而较低溶液质量分数的0.14 %及以下均表现出剪切增稠区间,再出现降解段。分析认为聚合物溶液的质量分数越高,分子线团越紧密,相互作用力越强,导致主链的相邻键偏离了正常键角的作用力较大,在不可抗拒的剪切外力作用进一步增加时分子链被瞬间扯断,弹性形态没有及时表现就直接断裂降黏;而低质量分数的聚合物分子线团相互之间的作用力较弱,在不断变化的剪切外力作用下,主链的相邻键偏离了正常键角,从而产生弹性恢复力,而表现出黏弹性,使表观黏度增加。HPAM 的临界剪切速率不受质量分数和剪切速率的影响,均在2 500 s-1左右,在当前测定条件下,其质量分数变化的影响会引起胀流段的出现。在临界剪切速率以内未发生机械剪切的HPAM,依然呈现典型的“剪切变稀”的幂律特征。
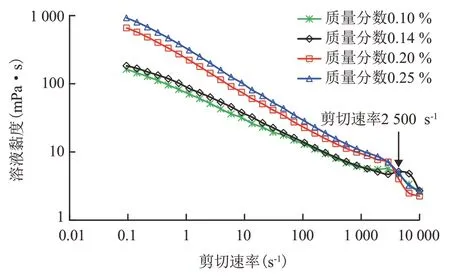
图5 HPAM的流变曲线Fig.5 Rheological curve of HPAM

图6 AP-P4的流变曲线Fig.6 Rheological curve of polymer AP-P4
虽然AP-P4 呈现了较好的“剪切变稀”特征,但是不同于HPAM,其流变剪切特征呈现“三段式”,在剪切速率为7~100 s-1时,黏度下降幅度较大,而过低的速率与过高的剪切速率时黏度下降幅度较低,这是疏水缔合作用增强了分子间的作用力,无论是分子内缔合作用,还是分子间的缔合作用均增强了聚合物溶液的内聚力,从而导致其剪切变稀的特征存在一定的变化。缔合作用并没有从本质上改变流变特征,细微的作用变化使其在较低和较高剪切速率条件下的黏度下降较为缓慢,表现出一定的抗剪切性。AP-P4 虽然在剪切流变区间中有一定的变化,但是整体上表现出了“三段式”的特征。
2.2.2 聚合物溶液流变模拟结果
对特征松弛时间约束,拟合的计算结果如表4所示。

表4 两种聚合物溶液的特征松弛时间Table 4 Characteristic relaxation time of two polymer solutions
通过对特征松弛时间范围的强制约束,降低了拟合过程中未知参数变量和算法的影响,特征松弛时间值条件的变化,大幅度地提高了拟合数据的研究意义。上述数据在公式的应用下形成的流变曲线与实验测得的一致性较高。其反向推导出的零剪切黏度,呈现出了聚合物溶液随着质量分数的增加,溶液内的相互作用力增强的特征。
3 结论
1)疏水缔合作用不仅仅大幅度提高聚合物溶液的表观黏度,其弹性作用也得到大幅度提升,所以实验条件下的黏弹模量实验数据中,AP-P4 以弹性模量特征为主导,而HPAM还是以黏性模量为主导。
2)通过小幅振荡实验数据推导的松弛时间谱,限制聚合物溶液特征松弛时间(λ)的取值范围,再应用Carreau-Yasuda 流变模型拟合聚合物溶液(HPAM和AP-P4)流变规律,不仅拟合精确度更高,而且可以避免非线性回归计算手段带来的计算误差,获得高度匹配实验数据的曲线特征。
