基于五转一移六自由度机械臂的运动学仿真

张元昕，张秋菊，杨 瑞

(江南大学 机械工程学院，无锡 214000)

关键字：六自由度机械臂；MATLAB；仿真；运动学

0 引言

目前的六自由度机械臂多应用在工业生产行业[1]，一般六个关节都为旋转关节，前三个关节用于定位机械臂在坐标系的整体位置，后三个自由度确定机械臂的末端姿态，并且主要是对机械臂的精度、速度、稳定性有较高的要求，而对于一些在整体空间大，操作空间小的环境中的作业很难进行。因此本文中设计了一种满足在特殊空间环境中作业的五转一移型六自由度机械臂。

对机器人技术的研究关键的一步就是进行运动学的分析，这也是运动控制的基础，因此本次对五轴机械臂的运动学分析与仿真至关重要。机械臂运动学分析即研究机械臂的运动特性，包括位置，速度，加速度，正，逆问题。而机械臂的位置正问题即正运动学，通过已知的关节角度进过计算获得齐次变换矩阵，从而计算出末端的位姿。由于机械臂的几何参数复杂繁琐，通常给各个连杆构建坐标系，通过描述坐标系之间的关系来表达机械臂的几何参数。使用较多的是Daneivt和Hartenberg提出的D-H模型[2]。但是D-H模型的Z轴编号和对应的关节编号不一致，不利于辨识，很多学者提出了改进的模型，比如Stone提出的改进D-H模型，即S-model，还有Judd提出的MDH模型和Veitschegger的五参数模型[3]。

机械臂位置逆问题则是通过已知的机械臂末端计算出机械臂各关节的角度。机械臂位置逆问题的求解方法一般分为封闭解和数值解法。封闭解包含消元法，吴文俊法，聚筛法等，数值解法主要有延拓法，迭代计算法等。随着技术的发展，还产生了遗传算法，神经网络算法等智能算法。

本文主要针对一平移五旋转的六自由度机械臂的设计结构，对其构建了MDH模型，利用消元法求得逆解，并且通过运用MATLAB仿真，验证分析六轴机械臂合理性。

1 六轴机械臂的结构设计

本文中机械臂具有五转一平移的六个自由度。如图1所示分别为肩关节，大臂关节，小臂关节，腕关节，腕部伸缩关节和末端旋转关节。其中腕部伸缩部分为平移关节，其余五个关节为旋转关节，使末端执行器能够到达工作范围内的各个目标点，能够保证机械臂末端姿态的空间位置和姿态，灵活实现纵向，横向，斜向等多方位姿态的作业需求，腕部的伸缩关节可以在整个机械臂满足工作空间的前提下通过末端执行器的伸缩对狭小空间的设备进行作业。

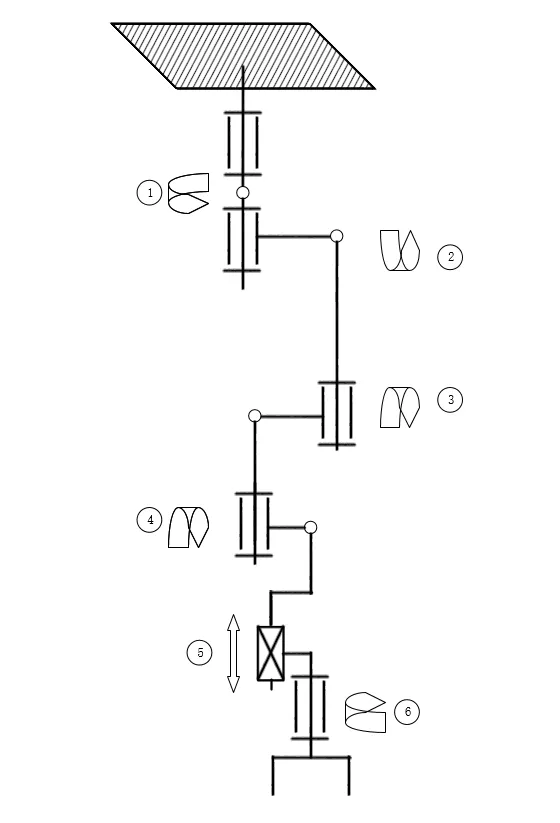
图1 六自由度机械臂结构简图

2 运动学分析

根据D-H模型的建立准则[4]，结合机械臂的实际尺寸参数，如图2所示，对六自由度机械臂建立D-H坐标系。其中基座标系{0}和坐标系{1}重合，坐标系{1}对应肩关

2 运动学分析

根据D-H模型的建立准则[4]，结合机械臂的实际尺寸参数，如图2所示，对六自由度机械臂建立D-H坐标系。其中基座标系{0}和坐标系{1}重合，坐标系{1}对应肩关节，坐标系{2}，{3}，{4}分别对应大臂关节，小臂关节和腕关节，坐标系{5}对应腕部伸缩移动关节，坐标系{6}对应末端旋转关节。表1中是机械臂的D-H模型的各个参数值。

图2 六自由度机械臂D-H矩阵坐标系

表1 D-H矩阵参数

2.1 运动学正解

正向运动学描述的是机械臂的关节空间到末端笛卡尔空间的映射关系，即已知各关节角度求解末端执行器工具点相对于基坐标系的位姿[6]。在建立坐标系后，将表1中D-H模型矩阵的各个参数代入到齐次变换矩阵中，其中各个关节角度θ1、θ2、θ3、θ4、d5、θ6为变量，其他各个参数值可以直接代入齐次变换矩阵中。机械臂的各个连杆的齐次变换矩阵依次为：

机械臂正运动学问题就是将已知的关节角度θ，求出机械臂的末端位置和姿态，即求出齐次变化矩阵0T6。现将上面各关节之间的变换矩阵相乘，则可以获得六自由度机械臂的相对于基坐标系的末端位姿矩阵，如下式：

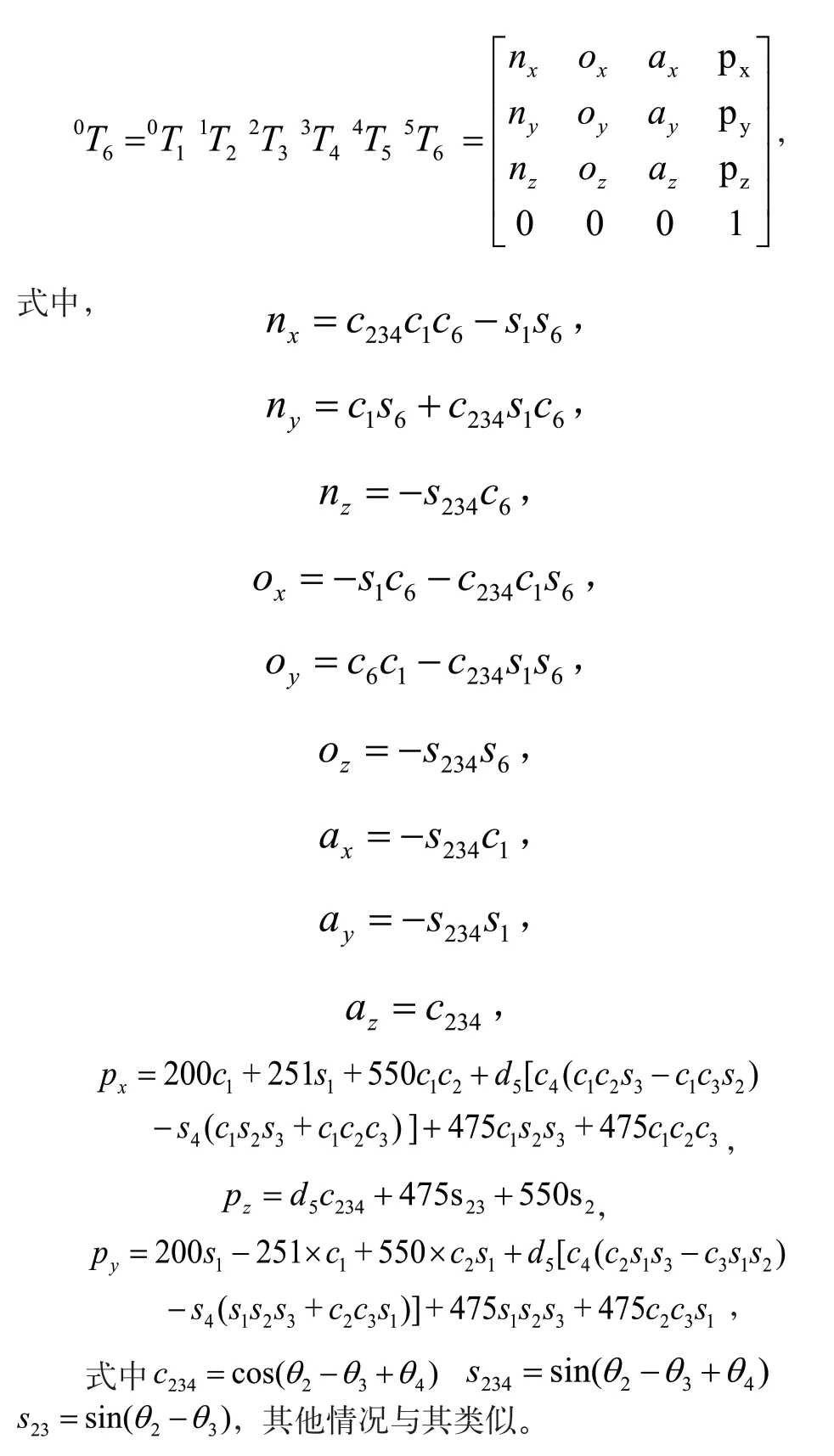
2.2 运动学逆解

机械臂的逆运动学问题，即将已知的末端位姿齐次变换矩阵0T6求解获得机械臂各个关节的角度θi[7]。本文中采用的方法是将运动学方程等式两边同时乘上相应的齐次转换矩阵的逆，令等式两边相等，从而获得关节角度解。

1）求解关节角度θ1，θ6

3 机械臂运动仿真

3.1 构建机械臂仿真模型

本文中，我们采用MATLAB的Robtics Toolbox机器人仿真工具箱对机械臂的运动学和轨迹规划等进行仿真。借助MATLAB仿真工具箱中的LINK()函数[8]，ROBOT()函数，DISPLAY()函数，TEACH()函数编程生成机械臂的运动学仿真模型，控制各个角度的控制面板和机械臂末端位姿坐标参数。如图3所示。

图3 控制面板和仿真模型

3.2 机械臂工作空间分析

机器人的工作空间即机器人末端参考点相对在基座坐标系所能到达的空间点的集合。机械臂的运动范围一般都是在一有限的区域内，例如本文中的六轴机械臂运动范围在以其完全伸直状态的机械臂长度为半径的近似球体的区域内，而在这范围内因为会有奇异点的存在，因此机械臂也就无法到达这些工作区域，这样机械臂的工作空间和灵活性就受到了限制。因此分析机械臂的工作空间也是十分有必要的。一般对机械臂工作空间的分析方式有解析法，数值法，描绘法等[9]。在本文中，采用了蒙特卡洛方法，以MATLAB编程实现六轴机械臂工作空间点云模型的构建。以下是在MATLAB中利用蒙特卡洛方法计算六轴机械臂工作空间的步骤：

1）对六轴机械臂进行正运动学求解，获得末端位置向量[px，py，pz]T；

2）利用MATLAB中rand()函数生成个关节变量的随机值，即：qi=qimin+(qimax-qimin)rand(1，n)。

式中：qi—第i关节变量；qimin—第i关节变量下限；qimax—第i关节变量上限；n—随机数个数。

3）将第2）步中的各个关节随机值代入末端位置向量[px，py，pz]T中求出六自由度机械臂的工作空间。

在MATLAB中运用蒙特卡洛方法进行编程仿真如图4所示[10]，图4(a)，图4(b)，图4(c)中机械臂工作空间在整体上基本保持在1.5m的范围以内，其中腕部长度为0.475m，上述仿真中设置d5为0.499m，由于第五关节为平移关节，因此图4中超出1.5m部分为腕部的伸缩量，为0.022m。从而也证明了本次机械臂设计合理，能够达到要求的工作空间。

这里本文分别对五转一移机械臂（图4）、常规六自由度机械臂（图5）、五自由度机械臂（图6）生成点云工作空间进行对比分析。这里将五转一移机械臂的移动关节变换为旋转关节构成常规六自由度机械臂，除去其平移关节构成五自由度机械臂。从图5、图6可以发现，在yOz视图和xOz视图的z轴方向±1.5m处会是一段直线，表明其工作空间就是一个半径为1.5m的球内，而从图4所示，由于拥有平移关节，其工作空间半径是最大伸缩距离加1.5m常规工作半径的和。当机械臂处于障碍物错综复杂的特殊环境中时，机械臂不能完全伸展，甚至只能保持一种状态时，则可以利用伸缩臂从障碍物间穿过，对工件进行作业操作。因此针对在这种特殊环境中的作业，五转一移机械臂相对常规的机械臂是十分有优势的。

图4 五转一移机械臂工作空间点云图

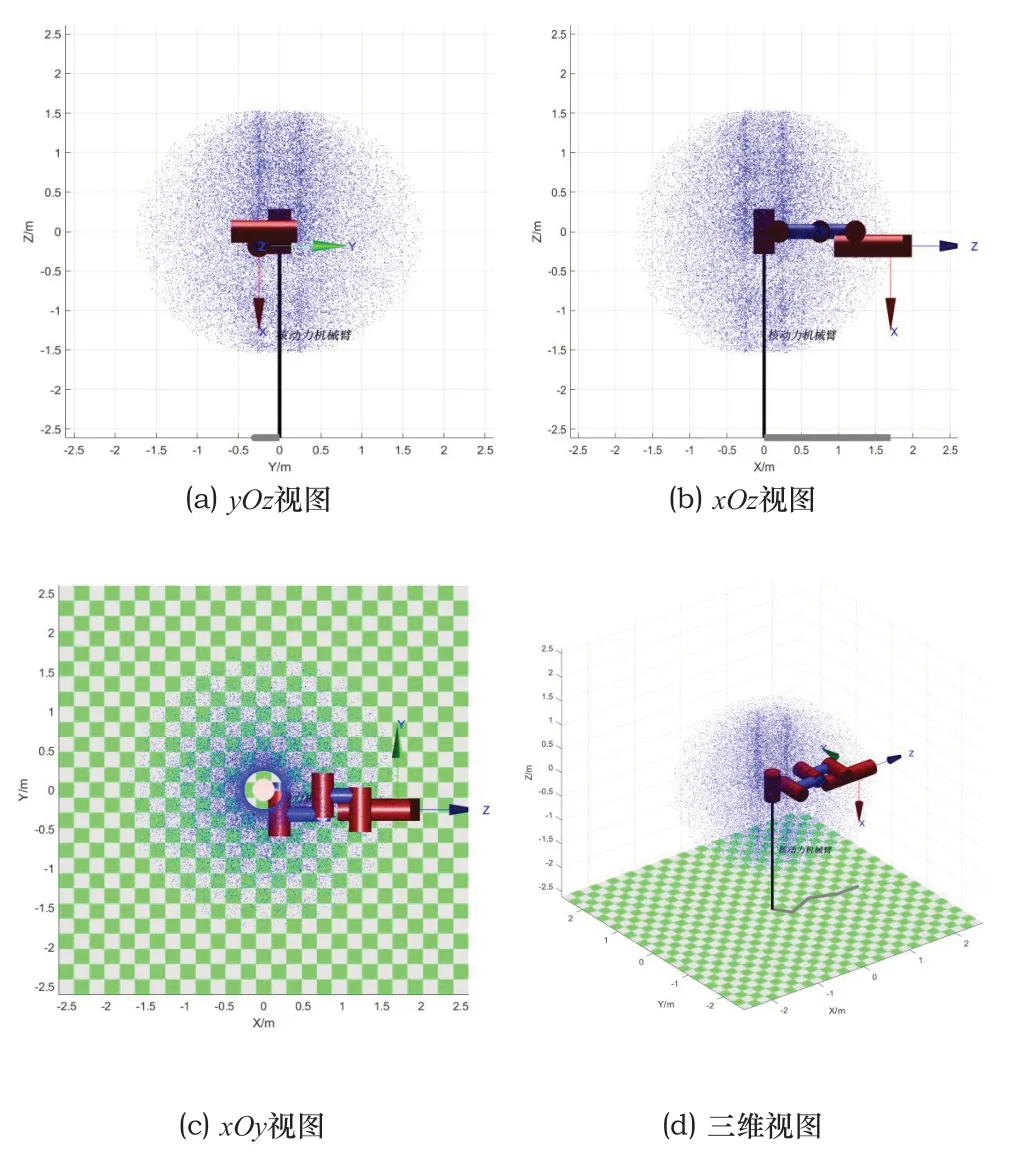
图5 六自由度机械臂工作空间点云图

图6 五自由度机械臂工作空间点云图

3.3 机械臂轨迹规划

上文中已在MATLAB 中构建了机械臂仿真模型，这里再初始化轨迹规划的相关参数，机械臂各关节的初始角度为θ0=(0，0，0，0，0，0，)，终止关节角度θi=(π/2，π/3，π/6，3π/20，0.5，π/4)[11]。设置仿真步数为40，在末端圆心处建立Marker点，以下为MATLAB中相关参数设置程序：

通过在MATLAB中编程显示出末端Marker点的位移，加速度，角加速度曲线和机械臂各个关节的位移，加速度，角加速度曲线。如图7～图12所示。

图7 各关节角度随时间的变化曲线图

图8 各关节角速度随时间的变化曲线图

图9 各关节角加速度随时间的变化曲线图

图10 末端执行器在三维空间的位置变化曲线图

图11 末端执行器速度大小随时间的变化曲线图

图12 末端执行器角速度大小随时间的变化曲线图

通过图7和上述对机械臂各关节初始角度和终止位置关节角度的设置对比，可以发现各关节角度随时间变化从最初的各关节角度值为0转动到各个关节相应的设置角度。图8中角速度的曲线偏移主要集中在15至25步之间，图9中角加速度在这一阶段趋于0，结合图8和图9，各关节角度呈现初始阶段的匀加速状态和中间匀速状态，到最终的匀减速状态，整个过程具有较高的稳定性[12]。图10至图12显示出末端执行器的各个参数变化曲线。结合图12和图11，末端执行器的角速度曲线偏移较大，在实际的操作中过大的速度会降低机械臂的使用寿命。因此可以利用多关节同时驱动减少末端位移，从而降低末端执行器的速度，保证机械臂平稳运行。

4 结语

本文针对特殊空间环境中废弃设备处理工作的需求，提出了一种五转一移的串联型六轴机械臂的解决方案。通过多关节联动和单关节点动，并且以较好的稳定性实现各种位姿变换的动作，利用蒙特卡洛法构建出机械臂的点云模型，直观地显示出五转一移型机械臂的工作空间，这种特殊结构也有利于机械臂在狭小操作空间内进行作业，同时也保证了机械臂能够到达设备室内的整体空间内的所有位置。利用D-H法对六轴机械臂进行运动学分析，首先在MATLAB中构建了仿真模型，获取机械臂末端位姿和各关节变量的解，然后计算出蒙特卡洛工作空间，最后采用机器人工具箱对机械臂末端及各关节进行了轨迹规划，验证了机械臂的结构设计的合理性，同时为后续的离线示教，结构优化提供了理论基础。