高烈度地区拱桥地震响应研究

2022-08-31史玉保

城市道桥与防洪 2022年7期

史玉保

（云南省城乡规划设计研究院，云南昆明 650228）

0 引言

桥梁作为国家交通基础设施的重要组成部分，在交通运输系统中发挥着不可替代的作用。而在已建成的桥梁中，拱桥因桥型之多、数量之巨而为各类桥型之冠。随着国家西部大开发战略的开展，云南省的基础建设得到了大力发展，拱桥因其良好的承载能力和经济性受到了广大桥梁设计师的青睐，在工程中被广泛使用。然而，随着桥梁使用年限的增长，桥梁在运营过程中可能会遭遇地震作用[1]，且云南省地处高烈度地区，更易遭遇强烈地震，这对桥梁的承载能力是一种极大的挑战，较高烈度的地震甚至会使桥梁不可修复，导致交通系统停滞和相关人员伤亡[2]。所以研究高烈度地震作用下桥梁的动力响应及主拱圈的承载能力，对今后该地区的拱桥设计有着重要的指导作用。

本文采用Midas Civil 有限元软件建立拱桥有限元模型[3]，通过反应谱法计算结构在不同烈度地震荷载作用下的响应，对计算结果进行分析，并与静力计算相对比，探究拱桥主要承重构件在地震作用下的承载能力[4]，为以后高烈度地区的桥梁选型提供参考。

1 工程概况

本文分析采用的桥梁模型为某5×46 m 连续拱桥，桥梁分两幅，单幅桥宽为25 cm 中央防撞护栏+11 m 机动车道+50 cm 机动车道防撞护栏+4.5 m非机动河道+5 m 人行道+25 cm 人行道栏杆=21.5 m，主拱圈截面采用实腹式矩形截面，截面高85 cm，桥面板采用π 型梁。拱圈、立柱及桥面板采用C40 混凝土，拱座、桥台及基础采用C30 混凝土。

2 拱桥结构模型建立

目前对桥梁结构进行受力分析常采用的是有限元方法，即基于结构的力和位移关系，将结构离散为杆件，在模型中反映出原结构的总体几何特征。该桥采用杆系结构建立桥梁模型，全桥结构采用梁单元进行模拟，桥面板与拱上立墙间支座采用弹性连接模拟，通过释放转动约束达到简支连接的目的，主拱与拱座、桥台使用共节点模拟其固定约束，桩、土间土弹簧刚度根据《公路桥涵地基与基础设计规范》（JTG 3363—2019）中的m 法进行计算，并采用节点弹性支撑和只受压弹性连接模拟。全桥模型如图1 所示。

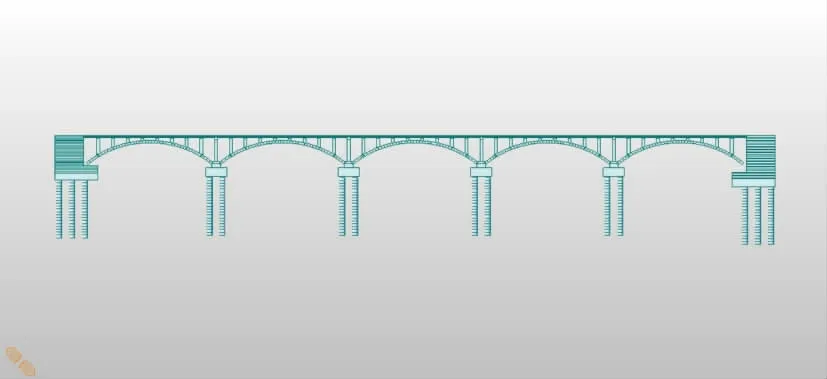
图1 全桥有限元模型

3 计算结果

3.1 静力计算结果

桥面铺装、防撞护栏、人行道板根据实际设计情况采用梁单元荷载添加，经过反复调试计算后，拟定拱轴线系数为2.1，恒载作用下拱桥内力计算结果如下：

由图2 和图3 可以看出，恒载作用下拱桥最大正弯矩为2 477 kN·m，最大负弯矩为-2 069 kN·m，现将每种荷载组合下的弯矩及对应的轴力导出，求得最大偏心距为0.07 m，根据《公路圬工桥涵设计规范》（JTG D61—2005）规定，主拱圈的偏心距应小于主拱圈有效截面的60%，该次实例主拱圈截面梁高为0.85 m，60%为0.51 m，可知该拱轴线系数满足要求。

图2 恒载作用下主拱圈轴力

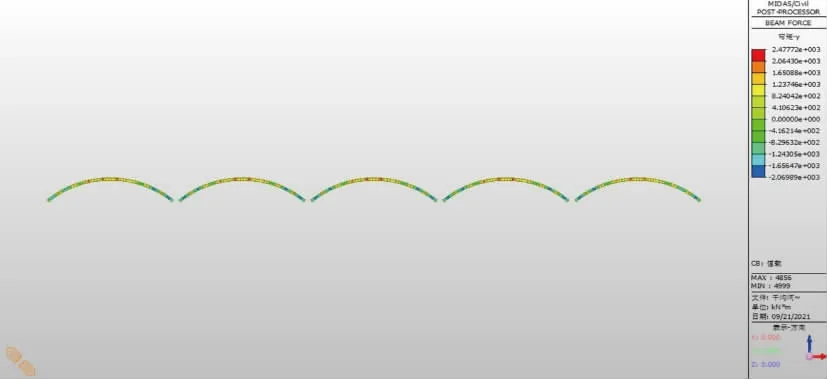
图3 恒载作用下主拱圈弯矩

3.2 结构自振频率

将荷载转化为质量，并采用多重Ritz 向量法进行特征值分析，X、Y、Z 三个方向的向量数量均设置为50 个后进行计算分析，根据计算结果，X、Y、Z 三个方向的50 个向量的合计振型参与质量分别为99.91%、99.97%和99.97%，大于《公路桥梁抗震设计规范》（JTG T 2231-01—2020）规定的90%，说明本次计算的振型数量满足计算要求，无需重新设置，拱桥主要振型及对应周期如下，因篇幅所限，只展示前3 阶振型，如图4 至图6 所示。

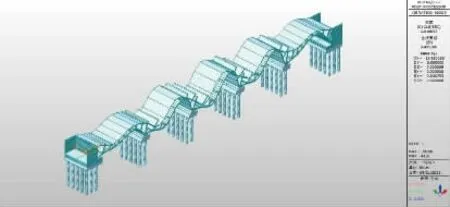
图4 模态1

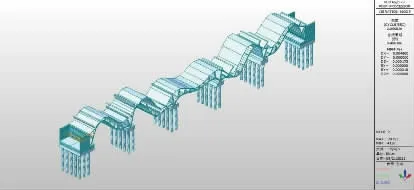
图5 模态2

图6 模态3

从上述图片可以看出，该桥的基本振型为纵桥向振型，横桥向及竖向振型多为高阶振型，由此反映出本桥的横向刚度相对较大，在地震作用下的结构损伤主要集中在纵桥向，因此，今后对该地区桥梁进行设计时，沿桥纵向的抗震措施应视情况提高一定的防护等级。

3.3 动力计算结果

本次计算采用多振型反应谱法进行，选取的地震烈度分别为7 度0.15g、8 度0.3g 和9 度0.4g，Ⅱ类场地特征周期为0.45g，根据《公路桥梁抗震设计规范》（JTG-T 2231-01—2020）规定，8 度及9 度设防等级的地区特征周期应提高0.05g，基于此，建立各烈度下的反应谱函数，函数曲线如图7 至图15 所示。

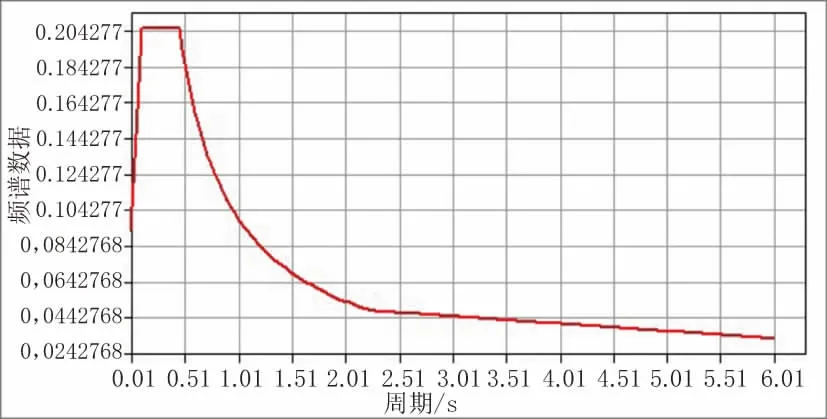
图7 7 度0.15g 反应谱函数

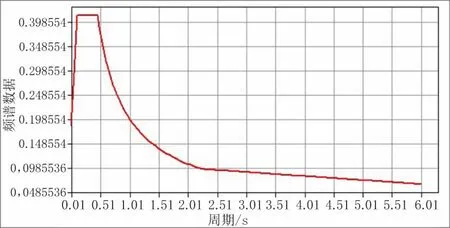
图8 8 度0.3g 反应谱函数

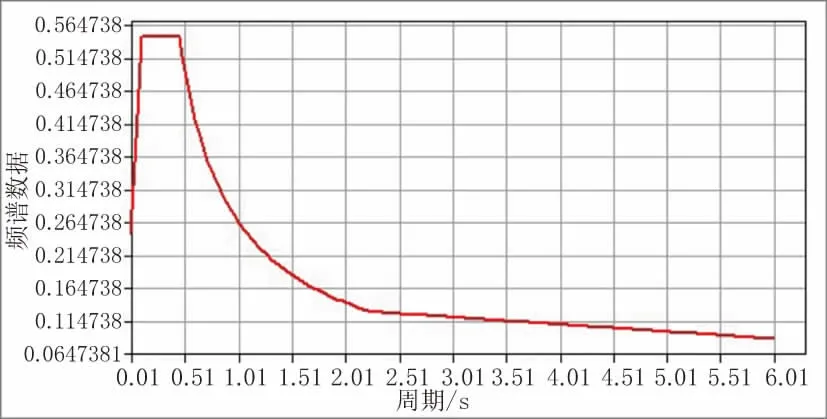
图9 9 度0.4g 反应谱函数

将反应谱函数代入模型计算后，得出不同地震烈度下，主拱圈内力如图10 至图15 所示。

图10 7 度0.15g 地震作用下主拱圈轴力

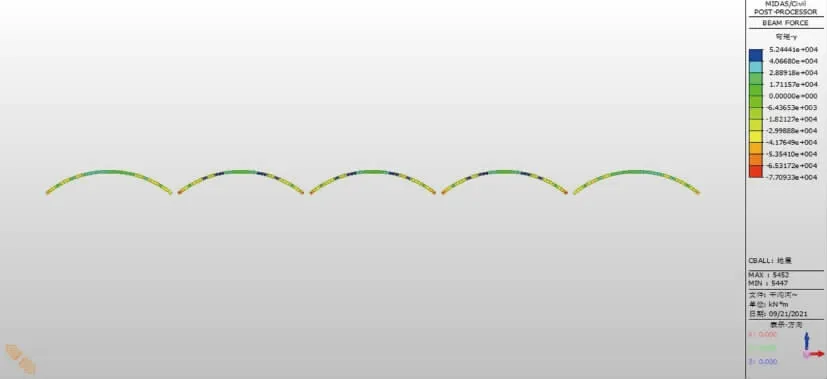
图15 9 度0.4g 地震作用下主拱圈弯矩

图11 8 度0.3g 地震作用下主拱圈轴力

图12 9 度0.4g 地震作用下主拱圈轴力

图13 7 度0.15g 地震作用下主拱圈弯矩

图14 8 度0.3g 地震作用下主拱圈弯矩

从上图可以看出，地震作用下，通过轴中间拱的轴力极大，证明连拱呈现出两边往中间挤的趋势，因此，今后在设计此类桥梁时，中间拱的地震响应应加大关注。

为方便对比拱桥内力的变化，现将静力和动力计算结果中的轴力、弯矩、偏心距最大值整理见表1。其中，静力计算结果采用基本组合下的设计内力。因为桥梁低阶振型主要为纵桥向阵型，因此表1 偏心距仅考虑纵桥向弯矩平面内的偏心距。

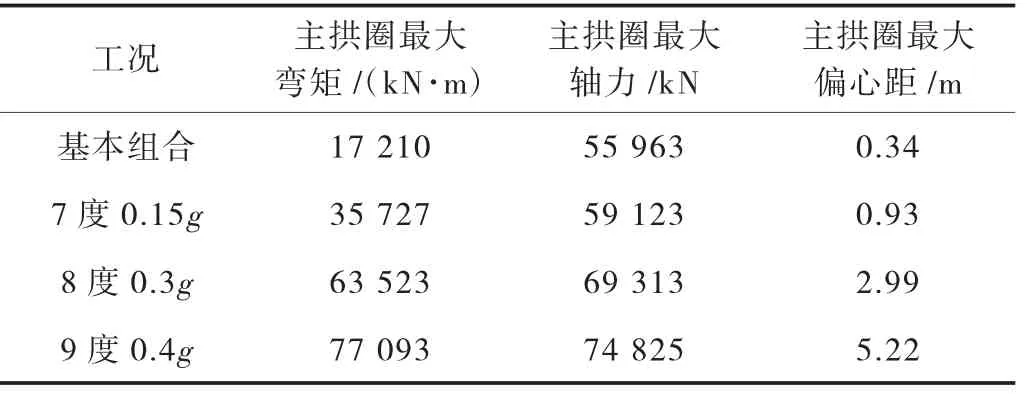
表1 轴力、弯矩、偏心距对比结果

从上表可以看出，随着地震烈度的增加，主拱圈的轴力、弯矩和偏心距有了明显的增加，将不同烈度下求得的轴力、弯矩、偏心距除以基本组合下的值所求得的放大系数如图16 所示，其中，系列1 为弯矩，系列2 为轴力，系列3 为偏心距。

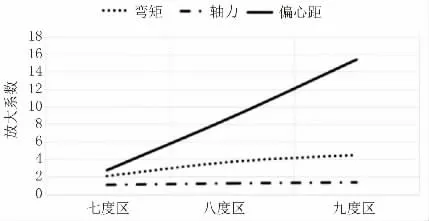
图16 弯矩、轴力、偏心距放大系数

从上图可以看出，随着地震烈度的增加，主拱圈的轴力增加较为平坦，而弯矩的增加幅度有了明显增加，偏心距的增加幅度极大，说明随着地震烈度的增加，拱桥对地震的弯矩响应敏感程度远远大于轴力敏感程度，而根据《公路桥梁抗震设计规范》（JTG-T 2231-01—2020）规定，主拱圈在地震作用下应保证一直处于弹性状态，因此，今后在高烈度地区对拱桥进行设计时，应酌情提高拱桥的抗震措施，必要时还应展开专项研究。