不等式恒成立问题的解法探究——2022年新高考全国Ⅱ卷数学第22题

廖梓豪

(华南师范大学数学科学学院 510631)

2022年的高考数学卷着眼于对数学思想方法和数学核心素养的考查，其中新高考Ⅱ卷第22题则是将导数、不等式、数列有机结合对学生进行考查.下面将对新高考Ⅱ卷第22题进行解答与分析.

1 试题呈现与评析

题目(2022年新高考Ⅱ卷第22题)已知函数f(x)=xeax-ex.

(1)当a=1时，讨论f(x)的单调性；

(2)当x>0时，f(x)<-1，求a的取值范围；

试题评析本题第(1)小问讨论函数单调性，主要考查函数与导数、单调性与导数的关系等知识；考查学生函数与方程、数形结合的数学思想以及运用基础知识解决数学问题的能力.第(2)小问主要考查函数与导数、不等式恒成立求参数取值范围的问题，考查学生对问题的分类讨论能力、逻辑推理能力以及数学建模能力.第(3)小问主要考查通过函数导数解决不等式的基本方法，实现问题的解决.本题充分体现了起点低，落点高，涉及知识点较多，有很强的综合性和灵活性，具有一定的区分度，自主探索性强，是一道考查学生数学素养和能力的优质题.

2 试题解法研究

第(1)问求导后容易判断单调性，这里解答从略.下面对第(2)问进行研究，相关解法如下.

2.1 第(2)问解析

思路1对参数讨论，转化为恒成立.

解法1若a≥1，由(1)知，当a=1时，f(x)的最小值为f(0)=-1，即xex-ex≥-1，所以当x>0时，f(x)≥-1，与题意矛盾；

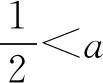
评注解法1是对参数进行分类讨论，进而将所证明不等式转化为恒成立问题，利用同构结合函数单调性进行证明解决，其中对参数分类讨论时节点的选取较为不易想到.

思路2 分离函数，数形结合.

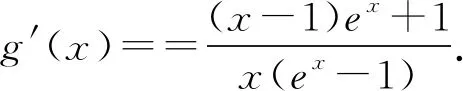
令h(x)=(x-1)ex+1，则h′(x)=xex>0，则h(x)在(0,+∞)上单调递增，即h(x)>h(0)=0，则g′(x)>0，则g(x)在(0,+∞)上单调递增.

原不等式恒成立等价于y=ax的图象位于y=g(x)的图象下方，临界情况为两函数图象相切，切点易知为x=0.由于g(x)在x=0处无定义，下面则对其导函数分析，

评注解法2是将所给不等式合理变形转化为f(x)>g(x)的形式，能够较容易地判断出不等号两边函数的图象关系.难点在于对g(x)及其导数在x=0的讨论，涉及到高等数学中的极限思想，较为复杂.

思路3构造含参函数，进行分类讨论.

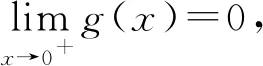
评注两种解法均为直接变形后移项构造函数，但后续对于导数结合不等式的放缩的讨论情况比较复杂，而对导函数求解零点的讨论相对简单.相比于解法1，2，这两种解法较为常规，同时也是构造含参函数解决不等式恒成立问题的一般思路.

2.2 第(3)问解析

解法2(构造函数，利用导数探讨恒成立)

评注此题的难点在于如何将不等式进行转化，第(3)问可以在第(2)问的基础上对问题进行解决，通过构造函数相对应的不等式，进而对x取值，得到数列型不等式，也可以直接观察所需证明的不等式与函数方程结合解决问题.本题将函数、导数、数列以及不等式等知识有机结合，考查学生灵活应用函数、不等式思想解决复杂问题的能力，对直观想象和逻辑推理能力也有较高的要求.

对导数的学习要淡化技巧, 重视基础, 回归问题的本质，掌握基本数学思想，注重通解通法.作为一名教师，教学中要巩固学生的知识基础，构建完整的知识体系，帮助学生将知识整合并对其系统化.此外，教师在解题教学过程中应当把握教学目标, 巩固学生对自身知识的认知, 坚持问题驱动原则，引导学生思考问题.充分利用数学思想进行解题指导，多角度尝试解决问题，从而培养学生的数学思维，提高数学素养.