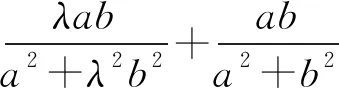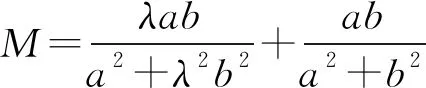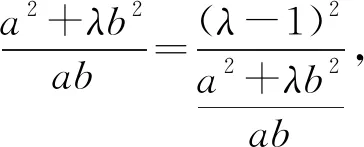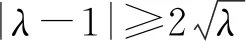对一道分式型二元最值问题的探究

李 寒

(贵州省贵阳市第一中学 550081)

本文通过对一道二元分式型齐二次条件最值题的探究，使学生学会数学地思考问题，优化数学思维品质.

1 试题重现

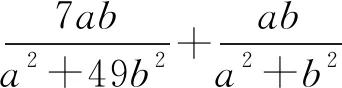
2 解法探究

解法1因为a>0，b>0，所以

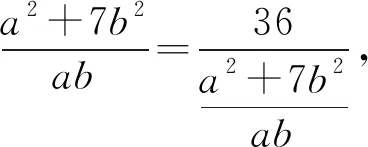
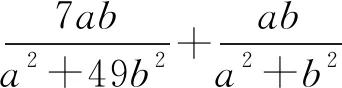
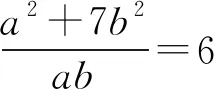
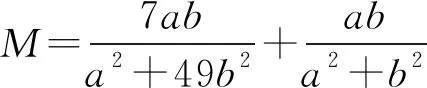
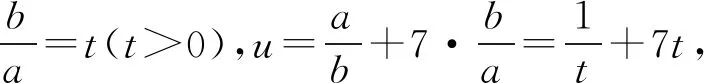
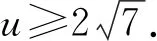
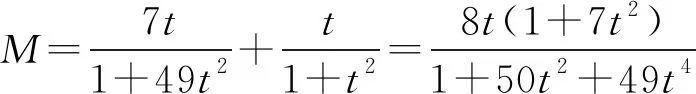
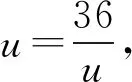
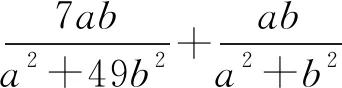
点评解法2首先进行比值换元和“二层”换元，然后进行代数恒等变换，变形出关于“二层”新元的均值不等式的结构形式，利用二元均值不等式求解.在运用均值不等式求最值时，“等号”能否取到是解答的关键.

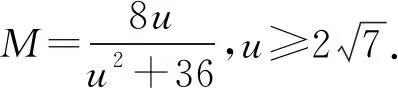
所以Mu2-8u+36M=0.

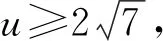
因为M>0，且二次函数y=Mu2-8u+36M的图象开口向上，

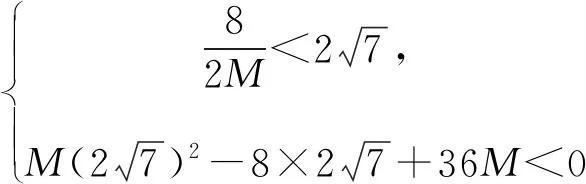
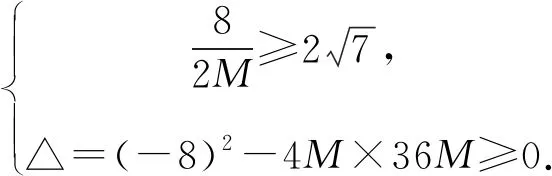
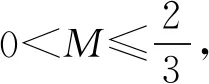
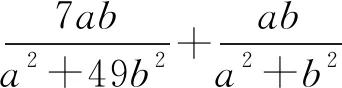
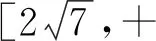
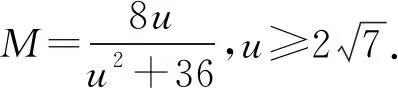
将M对u求导，得

所以当00，M在(0，6)上单调递增；当u>6时，M′<0，M在(6，+∞)上单调递减.

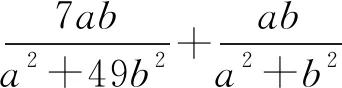
点评解法4是在解法2进行比值换元和“二层”换元的基础上求导，利用导数研究函数的单调性求解.利用导数求解二元条件最值问题是一种有创意的方法途径.

3 试题变式

若将上面赛题中的“系数”7换为5，那么求解的情况是怎样的呢？

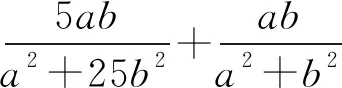
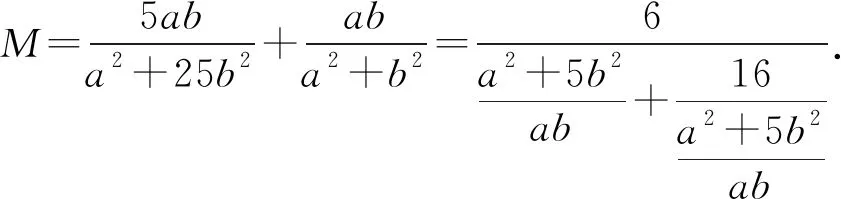
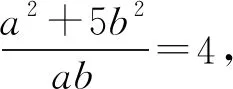
（1）强回声型：共计8例（其中左肺5例，右肺3例），声像特点为胎儿肺内有强回声包块，且边界较为清晰。并且回声的强度高于同侧其他部分以及对侧的肺组织。彩色多普勒血流显像提示4例胎儿的病灶内部存在体外循环血流，提示为隔离肺。

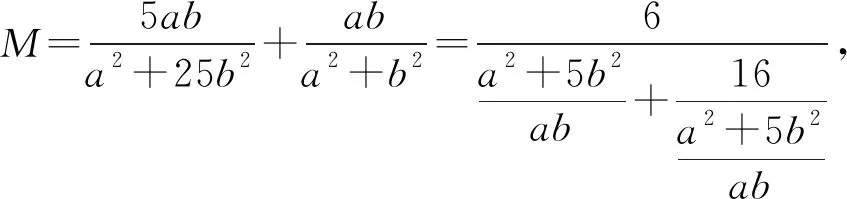
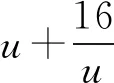
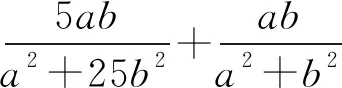
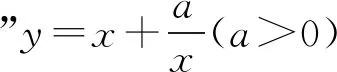
4 试题拓展