模拟退火优化的径向量核支持向量回归算法在人工嗅觉系统的应用
2022-08-30汪雨晴赵庆贺
汪雨晴,赵庆贺
(1.沈阳仪表科学研究院有限公司,辽宁沈阳 110043;2.东北农业大学电气与信息学院,黑龙江哈尔滨 150030)
0 引言
人工嗅觉传感器(electronic nose system)是工业生产中常用的环境检测系统,相比于色谱方法,具有低成本和高实时性的优势。目前的人工嗅觉传感器采用多传感器集成实现多种待测气体的隔离式检测方式,各组的仪器响应和预测值是作为独立样本进行拟合建模的,预测过程受到环境中其他气体和传感器漂移的双重影响,对实时监测过程的精度有很大的负面影响[1]
随着机器学习和人工智能方法的快速发展,针对适用人工嗅觉传感器系统的高准确度模型及系统研究逐渐成为热点,H. Fan等应用电化学传感器阵列完成了开放环境的气体聚类鉴别[3]。J. Burgués等开发了一种基于人工嗅觉的无人机用工业环境空气质量量化系统[4]。P. Asha等设计了基于物联网和人工智能方法的多传感器环境监测人工嗅觉系统[5]。
非甲烷总烃(non-methane hydrocarbons,NMHC)是指空气中除甲烷外的气体烃类化合物,主要是工业环境含碳有机物的副产物,是大气环境中的废气之一[6]。传统的NMHC检测需依照《固定污染源废气:总烃、甲烷和非甲烷总烃的测定:气相色谱法》(HJ 38—2017)完成,作为基于色谱学的实验室方法,无法完成实时性的检测[8]。人工嗅觉方法作为一种高效且实时的方法在NMHC检测中具有良好的应用前景。
为提高人工嗅觉系统在实时监测中的准确性,本文提出了一种基于融合多通道传感器数据的记忆序列模型,利用7通道(5种气体及温湿度数据)仪器响应和长度为4的记忆多维度数据,结合模拟退火优化的rbf-svr模型作为拟合算法,对比传统的线性模型可将R2从0.924 8提升至0.984 1,MAE指标从41.057 5提升至15.244 4。
1 人工嗅觉系统的有记忆多通道仪器响应
人工嗅觉系统的核心包括数据采集模块和计算单元模块,如图1所示。数据采集模块由单一气体传感器或气体传感器阵列构成,将表征环境气体浓度信息的化学信号转化为传感器的电信号,最终作为仪器响应值输入计算单元。计算单元将仪器响应值和预测值进行转化,完成拟合计算后,最终将电信号强度转换为具有实际物理意义的观察值,完成仪表检测任务[6,9]。
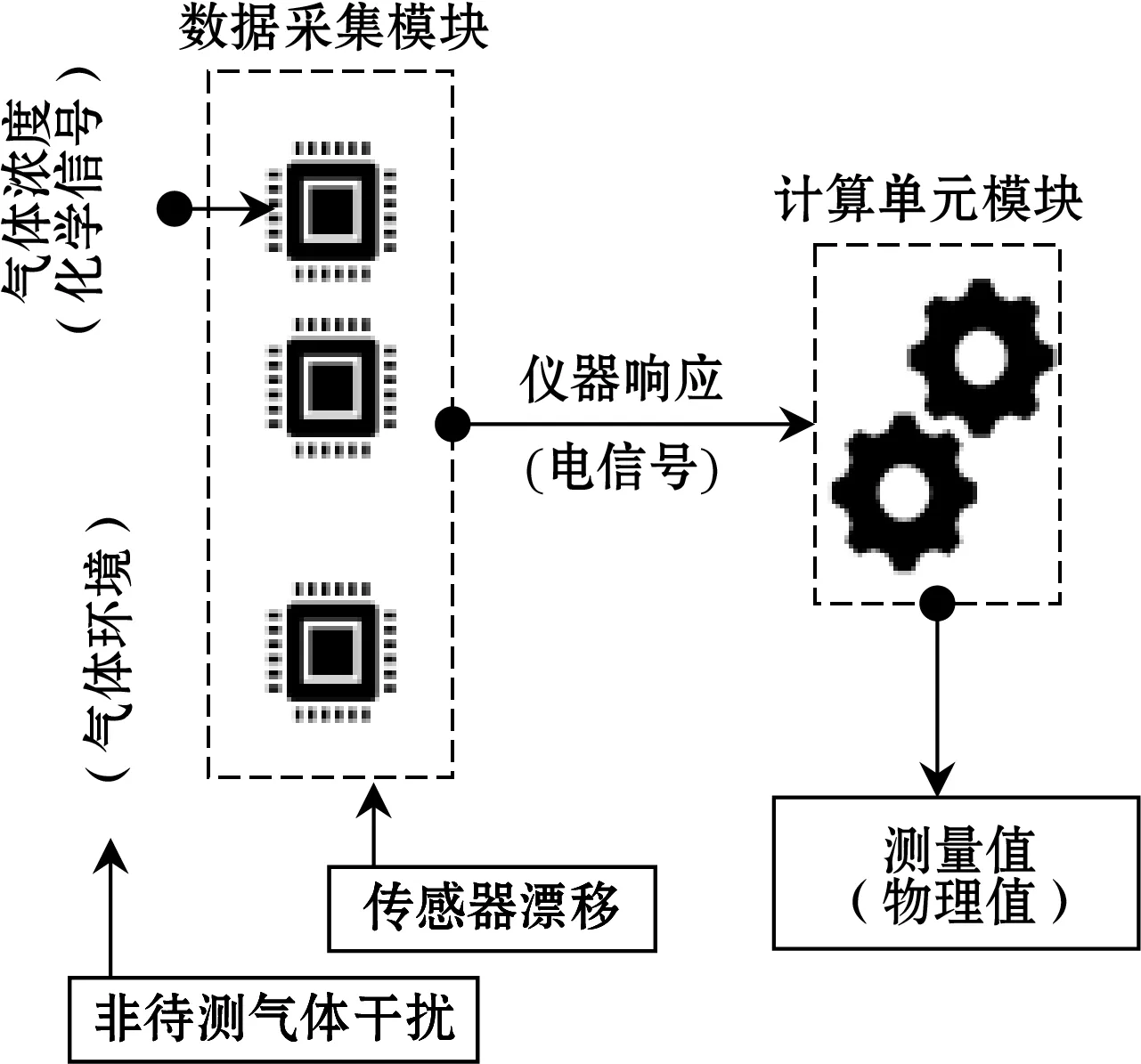
图1 复杂气体环境下人工嗅觉系统示意图
该过程中,数据采集模块的传感器部分是将待测气体信息转化为仪器响应的关键核心部分,但实际的应用过程中,传感器或传感器阵列会受到环境温湿度、环境中干扰气体成分和自身运行漂移的影响,从而造成响应值和真实值的非线性偏差[6,10]。
对于非监测气体的干扰,传统的解决方法是尽可能在数据收集侧减少异常气体的干扰,但实际应用的环境中,气体的种类与含量都具有高度不确定性,采用抗干扰能力更强的传感器阵列会加大应用的成本。另一方面,从实际的气体分布环境角度而言,环境中的气体含量是存在相关性的,以本文关注的NMHC气体为例,其自身是有机物化学反应过程中产生的混合烃类气体,当有机物产生时,环境中的CO、CH4等同样会产生变化,各类气体的含量最终会达到空气中的动态平衡,因此这样的复杂气体环境是人工嗅觉系统的工作常态。
针对人工嗅觉系统中复杂气体环境下非监测气体的干扰问题,本文结合多通道传感器可同时获取多路仪器响应值的特点,将多路响应值作为共同特征,完成多维度响应数据集的构建,进一步选择具有适合多维度数据回归拟合的方法建模,即带有rbf核的支持向量回归方法,并引入模拟退火方法,构成sa-rbf-svr模型进一步完善多维度拟合预测NMHC气体浓度的效果。
对于传感器的漂移现象,本质上是随系统采集时间的增加,传感器自身发生老化或环境气体吸附造成传感器中毒引出的误差,可视为y=f(x,t)中引入了时间变量对模型造成的影响。这种影响可以采用引入时间特征,或加入基于时间特征的修正系数进行修正[9]。
针对人工嗅觉系统的传感器漂移问题,本文将前时刻仪器响应纳入模型,作为记忆维度进行动态补偿。相比于时间特征或修正系数,这种结合了记忆响应的数据能具有更有效的信息量。
图2是本文数据输入部分的结构,记忆序列部分的引入将抑制随时间变化的传感器漂移,多通道响应的引入将抑制其他气体在检测过程中产生的干扰。这样的数据结构不仅包含了多维度数据的特点,也结合了时间序列数据的部分特点,但传统的线性模型拟合效果一般,因此本文设计了基于机器学习方法的支持向量机模型(support vector machine,SVM),通过历史数据完成模型建立,并针对高维度的记忆序列特点,引入了基于模拟退火方法的回归模型优化方法。
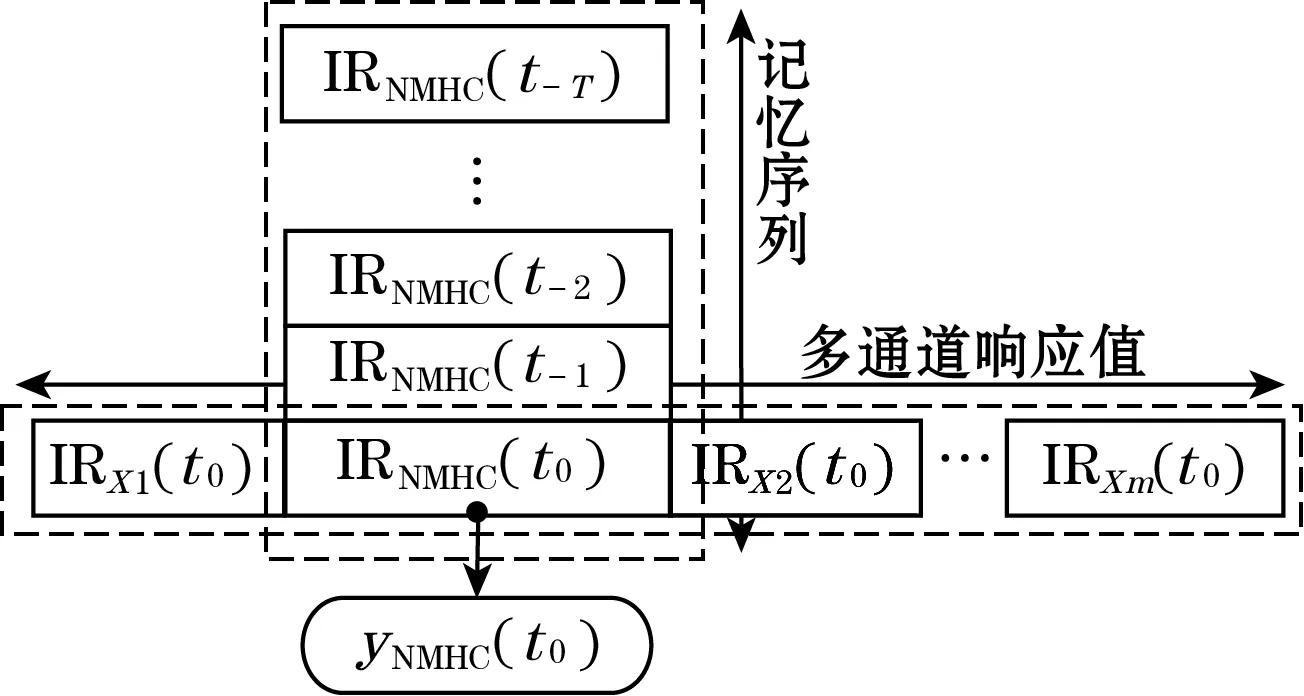
图2 有记忆的多通道仪器响应数据结构
2 模拟退火优化的径向量核支持向量回归模型
支持向量回归(support vector regression,SVR)是Vladimir Vapnik提出的支持向量机监督学习算法在回归问题中的变种,是机器学习中被广泛应用的高性能高稳健性算法[11]。高维空间中,SVR通过凸优化过程,迭代完成构建超平面,完成实现样本的有损划分,最终依靠过程中的支持向量(support vector,SV)完成回归任务。此过程可以构建为如下模型:
(1)
式中:ω和b是构成超平面y=wX+b的点法参数;φ(xi)是xi向希尔伯特空间的映射;C,ε和ζ是线性不可分过程中的软间隔(soft margin)的惩罚项,C为惩罚强度,ε为对ζ和ζ*的边界误差允许程度。
该问题的拉格朗日对偶问题如下,两者满足Karush-Kuhn-Tucker条件,可等价求解(2):
(2)
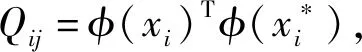
(3)

式中:γ为rbf核函数的转换强度。
该过程中涉及到3个关键的超参数:决定了正则化惩罚强度的C和ε,以及rbf核中的γ。三者共同决定了SVR迭代过程中SV的求取,最终直接影响模型的精度和泛化能力,此模型即为rbf-svr模型。
本文在超参数配置过程中采用了模拟退火算法(simulated annealing,SA)完成求解。SA算法是一种带有随机过程的元启发算法,是对金属加工过程中退火过程的模仿[12-13]。rbf-svr模型配合SA算法的过程如图3所示,其中H为C、ε和γ构成的超参数分布集合:

图3 模拟退火优化算法流程图
(1)初始化过程:配置初代指标参数s0=0,H=H0,H0为待搜索超参数的初始集。
(2)结合训练数据x后,得到次代指标s。
(3)当s>s0时,代表新状态更优秀,直接更新H0=H与s0=s;
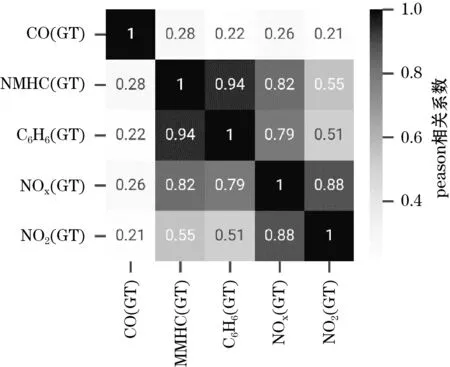
(4)如果s (5)更新迭代世代数k,并进行判断,如果k达到迭代上限,输出此时的H0作为最优解;否则,对H加入search space的扰动量。 重复(2)至(5)过程,直到达成输出条件。 本文人工嗅觉仪器响应数据由意大利国家新技术、能源和可持续经济发展局(ENEA,national agency for new technologies,energy and sustainable economic development)提供[14]。 该数据采集自Pirelli实验室开发的多通道人工嗅觉传感器系统,其中传感器阵列采用金属氧化物化学电阻传感器,可同时采集5种污染物仪器响应值,简要特性如表1所示。 表1 多通道人工嗅觉传感器参数 ENEA同时提供了相关固定观测站的5种空气污染物的测量真值和采样地点的温湿度信息。针对如上数据集,截取时间间隔1 h的约15 d样本,计算成对的相关系数得到如图4所示,从相关系数矩阵可知,本文焦距的NMHC与其他4种污染物的真值间存在较高的相关性,和C6H6及NOx之间的peason相关系数分别为0.944 3及0.819 7。 图4 5类污染物的peason积累相关系数矩阵 本文取5通道传感器的响应数值和温湿度信息作为样本数据集,取NMHC真值作为拟合目标值,采样间隔为1h,采样范围约15 d,得到182个样本的7维度原始数据集。将每个样本点的前4个时刻的NMHC响应值加入样本,得到合计11维的178个有记忆样本点。 将数据集中前130个样本点作为训练集,该集合用来拟合模型;中间间隔24个样本点后,以末尾24个样本点作为测试集,用来评价模型的泛化能力。 对于模型的整体拟合效果,采用决定系数(coefficient of determination,R2)和平均绝对误差(mean absolute error,MAE)评价。 决定系数R2的计算方式如下, (5) 决定系数R2是拟合优度的指标,合法区间为[-1,1],越接近于1的指标,代表模型拟合效果越出色。 平均绝对误差的计算方式如下: (6) MAE代表样本集成对的真值与观察值误差的整体分布,具有和真值相同的物理量纲,越接近于0的指标,代表拟合误差越小。 对于拟合中的可能出现的异常结果,采用MedAE和最大误差(Max error)计算。 (7) (8) MedAE和MaxError分别度量了残差集中的中位数和最大值,参照两者可以对模型拟合过程中存在异常结果的稳健性进行平均,两者的值越小,代表模型稳健性越强。 模型采用python3.9编程环境,svm家族模型采用libvim实现,偏最小二乘和弹性网线性模型采用scikit-learn实现,计算环境见表2。 表2 算法实现计算环境 为保证实验过程中的现象可复现,实验配置全部随机数种子为615。数据转换、预处理及样本异常值处理采用numpy和pandas完成。对于SA算法,采用hyperactive完成配置。 实验数据及模型源代码已完成开源,可在MIT许可协议下获取及测试[15]。 对照实验中采用2种线性模型和2种svr模型参数。线性偏最小二乘回归模型(oplsr)和经3-flods交叉检验确定系数的弹性网回归模型(en3)[16]作为线性模型的对照组,linear-svr为线性核svr模型,该模型和rbf-svr模型配置为同样的共有超参数。 配置起始温度数值为1.00,退火过程中接受妥协的概率为0.90,单次退火过程的邻域候选点数为5,随机过程产生的随机数满足高斯分布。 搜索空间中,配置C为[1,10 000]的离散整型数,间隔为1;配置svr惩罚项ε和rbf核转换强度γ的空间为初始数值上下各1个数量级的10 000个样本点。对于ε的初值,按照文献[17]配置为nsamples×var(X)的倒数。完成模拟退火参数和搜索空间配置后,进行104次迭代退火。 对于退火算法的评价指标,采用5-flods的交叉检验完成,并进一步在每flod中采用训练集的5-flods求解平均R2作为评价指标,以构建双cross validation过程确保泛化性能最大化。迭代过程中的rbf-svr函数限制迭代上限次数为103次,确保最终得到的优化模型具有抗过拟合的性能。 sa-rbf-svr在最终数据集(better-svr_d3)的优化迭代过程如图5所示,x-y-z轴分别为C-γ-ε的取值,空间点颜色深度为5-flods得到的训练集R2平均值。在搜索空间立方中,只有C-ε平面的高精度的点分布均匀,证明SA过程中对kernel自身的转换强度更偏重,可知模型的训练精度对rbf函数中γ系数的更为依赖。 图5 基于模拟退火的rbf-svr优化的三维可视过程 将实验结果按决定系数R2排序,如表3所示,d1和d2分别代表传感器单通道和多通道的响应数据,d3是融合了NMHC前4个时序的响应的有记忆数据集。better-svr表示sa-rbf-svr模型。svr类模型相比线性模型具有更优秀的性能。基于R2指标,sa-rbf-svr模型在结合了记忆的多通道数据d3中,具有0.984 1的R2指标,在所有测试集结果中表现最好,偏最小二乘回归oplsr和3折弹性网回归en3模型,在分别与d3和d2结合后,可得到0.978 8和0.978 1的决定系数,分别代表了两类线性模型的最优结果。在测试集中,sa-rbf-svr模型具有最好的拟合效果。 图6是针对拟合实际情况的MAPE绘制的条形对比图,该项指标代表了完成了归一化指标的MAE的距离,linear-svr的3种MAPE指标均环比最劣,对应的在表3中,其相关系数在d1模式下为负值,d2和d3模式下也较为低下。在各类数据模型中的linear-svr均表现不佳,这和rbf-svr和sa-rbf-svr形成了鲜明对比。 表3 对比建模效果评价 图6 线性模型与svr模型的MAPE对比 以oplsr模型作为线性模型代表和sa-rbf-svr对比,将测试集中MAE、MaxError和MedAE三项指标绘制雷达图(见图7),由图7可知,两类svr模型,实际上具有更大的最大误差,但尽可能将中位数误差控制在一定范围内。偏最小二乘回归模型oplsr和3折弹性网回归的R2指标和最优的sa-rbf-svr相近,但根据MAPE的对比,这两类线性模型的表现均无法和sa-rbf-svr对比。 图7 线性模型与sa-rbf-svr稳定性三维指标雷达图 图8将测试集的预测结果和真值进行比较,可见oplsr_d2模型的高R2指标,是对若干极端点的拟合贡献的,实际拟合过程中的贴合度并非R2反应的确切。对于测试集中的局部极值样本拟合效果,如1 d和11 d两处的尖峰,以及14 d处的下转折点,点折线条表示的oplsr_d3贴合紧密,但其他样本的拟合程度则不如svr模型准确。因此,实际应用效果中,oplsr的实用性不如sa-rbf-svm。 图8 真实值与回归结果对比 人工嗅觉传感器系统应用中,通过对比单通道拟合单项数据的数据集d1与多通道共同作用的数据集d2,可知应用多维仪器响应作为数据集,可以更加准确的拟合单项气体数据的浓度。通过对比有记忆的数据集d3与无记忆的数据集d2各项模型的指标后,可知将仪器响应历史记忆数据的引入,可进一步提高人工嗅觉系统的识别精度。 在人工嗅觉系统多维响应建模的过程,svr算法比传统的线性算法具有更好的拟合强度,但此过程需要正确配置kernel函数,并将对应超参数合理选择。对于核函数,rbf核函数相比于linear核具有更好的拟合效果,对于超参数选择,sa方法引入后的sa-rbf-svr可以进一步将支持向量回归的性能提升。 综上所述,sa-rbf-svr模型结合有记忆多仪器响应的数据的气体模型识别具有更好的预测性能,结合带有记忆的多维度数据,可将R2从0.924 8提升至0.984 1,MAE指标从41.057 5提升至15.244 4。可有效改善人工嗅觉系统中的识别过程。3 实验设计与验证
3.1 数据集与数据相关性分析

3.2 模型评价指标
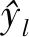
3.3 算法实现环境

4 实验结果与分析
4.1 线性模型建模与模拟退火优化过程分析

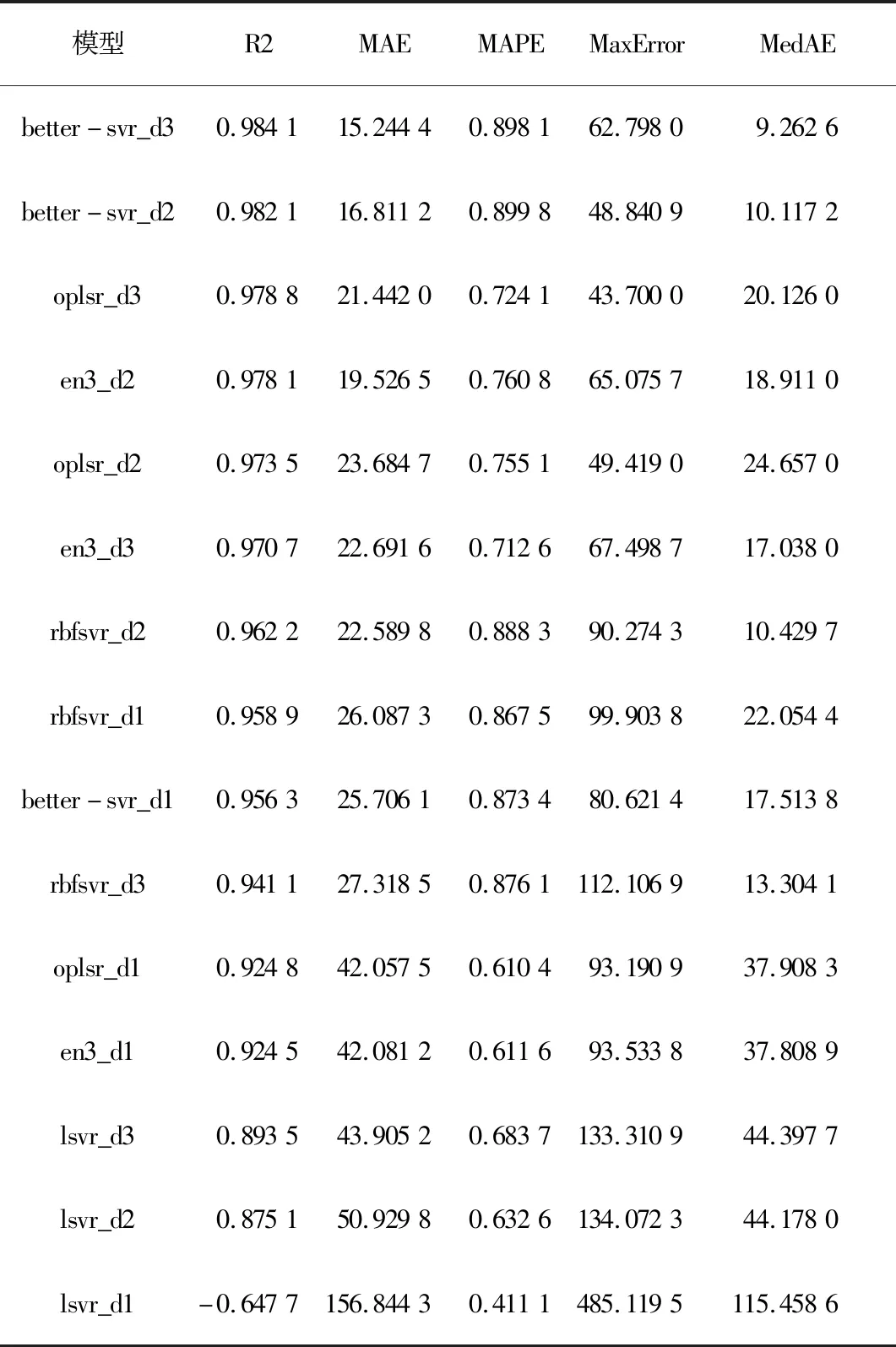
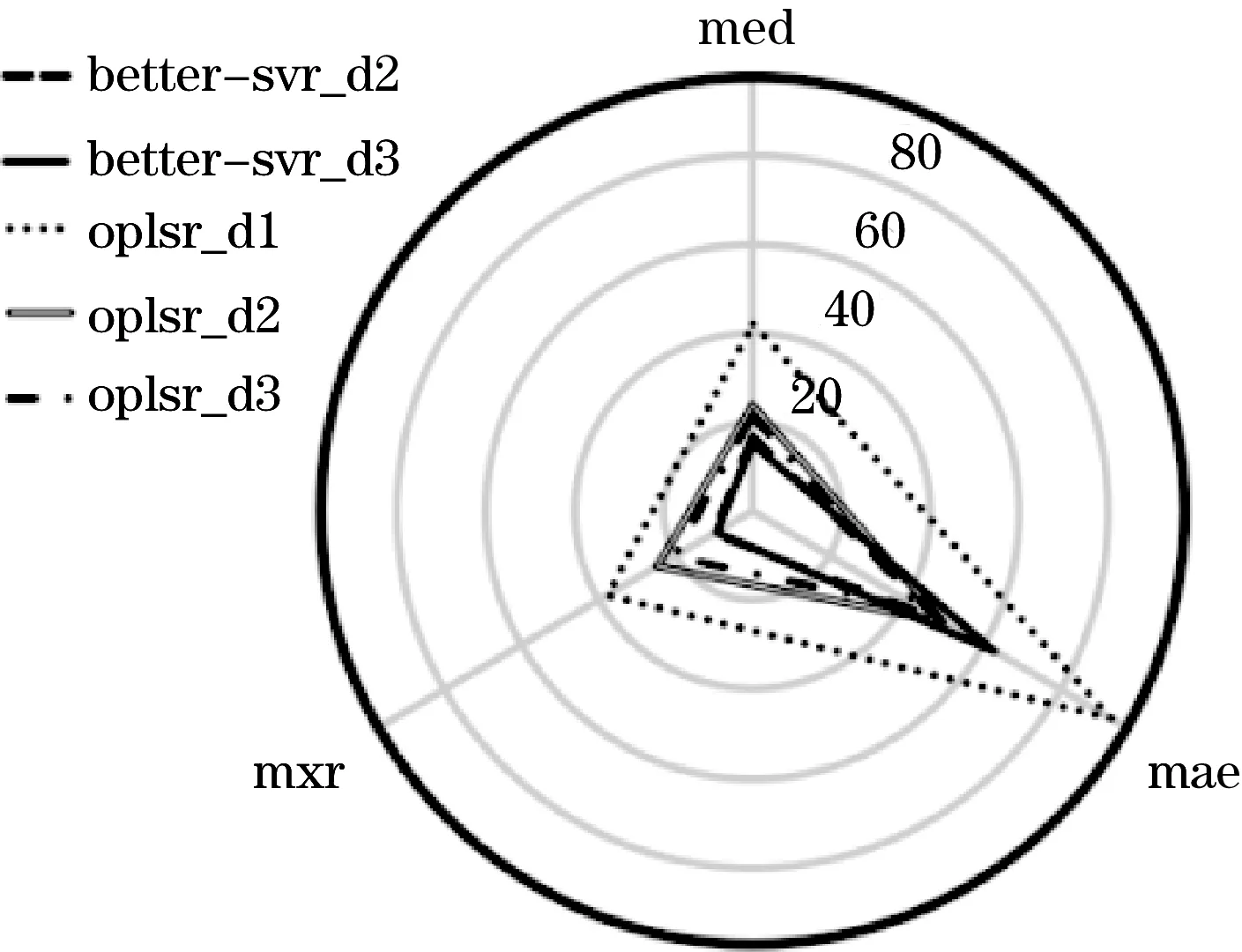
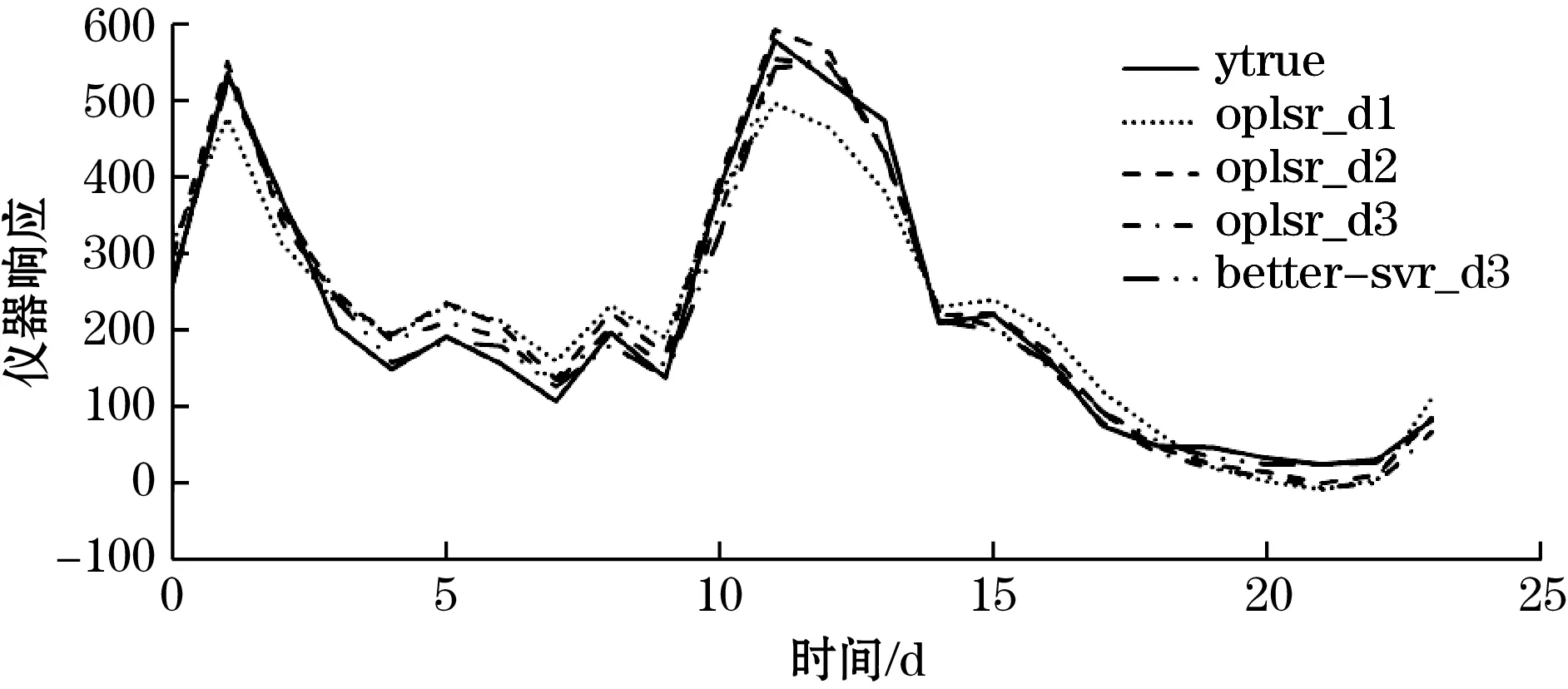
4.2 结果分析

5 结论
