Stability of Viscous Shock Wave for One-Dimensional Compressible Navier-Stokes System

Lin Chang

(School of Mathematical Sciences, Beihang University, Beijing 100191, China)

Abstract: In this article, the nonlinear stability of viscous shock wave for 1-D compressible Navier-Stokes system is studied. By the standard local existence method, it is found that the solution exists on a finite time interval [0,T] (T<∞). However, this method is not available for global existence since the solution may blow up as time t tends to infinity. Thus a priori estimate needs to be established, which can reduce the upper bound of the solution on the time interval [0,T]. Moreover, the bound of the solution at time t=T is made equal to the bound at the initial time. By the same method, it is known the solution exists on [T,2T],[2T,3T],….Thus the global existence of the solution is obtained. During the process of obtaining a priori estimate by the standard method, some additional conditions are proposed. To weaken those conditions, two suitable weighted functions were chosen, a double side weighted energy method was used, and a priori estimate was obtained under some weaker conditions. Thus when the adiabatic exponent γ satisfies 1<γ<1.5, the solution not only exists globally but also tends to a viscous shock wave as time goes to infinity.

Keywords: initial value problem; viscous shock; asymptotic stability

0 Introduction

In this paper, the initial value problem of one-dimensional compressible non-isentropic Navier-Stokes system for ideal gas is investigated, which reads in the Lagrangian coordinate as[1]

(1)

The unknown functionv(x,t)>0 represents the specific volume, the unknown functionu(x,t)is the velocity, the unknown functionp(x,t)represents the pressure, the unknown functione(x,t)stands for the internal energy, and the unknown functionθ(x,t)>0 is the absolute temperature. The positive coefficientμstands for the heat-conductivity coefficient. The coefficientκ>0 stands for the viscosity coefficient. For ideal gas, there is[2]

whereB,Care two positive constants,R>0,S,γ>1 are the gas constant, specific entropy, and the adiabatic exponent, respectively.

The initial value problem was investigated for expression (1) equipped with the initial data

(v,u,θ)(0,x)=(v0,u0,θ0)(x)，x∈

(2)

and the far field condition:

Consider the case where entropySis a constant. So the pressure becomesp=p(v)=a(v)-γfor constanta. Thus expression (1) become

(3)

and the corresponding initial condition is

(4)

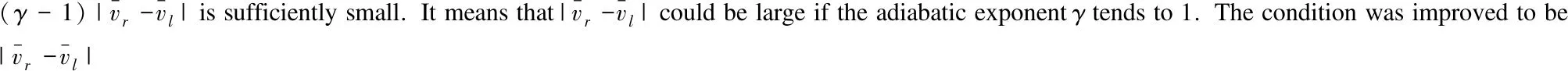
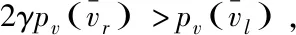
The rest of the article is arranged as follows. In Section 1, some properties of the viscous shock wave are proposed and the main result is described. In Section 2, the original problem is reformulated by the anti-derivative method. In Section 3, the a prior estimation is obtained by a weighted energy estimate.

1 Viscous Shock Wave and Main Result

Setζ=x-σt, whereσis a constant indicating the speed of the shock, which will be determined later. The travel wave solution (vs,us,θs)(ζ) of expression (1) is considered to be

(5)

And

(6)

where

Integrating expression (5) concerningζwith (ζ,∞) or (ζ,-∞), there is

(7)

(8)

For simplicity, the focus of this paper is on the caseσ>0 (third shock). Furthermore, it is assumed that the shock speedσsatisfies the following Lax’s shock condition:

(9)

(10)

Next, the main result of this study is to be described. Suppose that

(v0-vs,u0-us,θ0-θs)∈H1

(11)

(Ψ0,Φ0,Z0)∈L2

(12)

So

(13)

Define

Then the result can be stated as:

(14)

The Cauchy problem as shown expressions (1) and (2) has a unique global solution (v,u,θ)(x,t) such that

and the long time behavior

2 Reformulation of Problem

The perturbation is defined as

(χ,φ,z)(t,x)=(v,u,θ)(t,x)-(vs,us,θs)(ζ),ζ=x-σt

With the aid of expressions (1) and (5), it is known the perturbation (χ,φ,z) satisfies

(15)

where

(16)

and

(17)

with

(χ0,φ0,z0)(x)∶=(χ,φ,z)(0,x)=

(v0-vs,u0-us,θ0-θs)(x)

(18)

where

(19)

and

O(1)|(χ,φ,z,φx,zx)|2

(20)

with

(Ψ0,Φ0,Z0)(x)∶=(Ψ,Φ,Z)(0,x)

(21)

The solution space of the Cauchy problem as shown in expressions (18) and (21) is defined as

δ(0,T)={(Ψ,Φ,Z)∈C0(0,T;H2)

Ψx∈L2(0,T;H1)

(Φx,Zx)∈L2(0,T;H2)

Proposition2.1(a priori estimate) It is assumed that (Ψ,Φ,Z)∈δ(0,T) is the solution of the problem as shown in expressions (18) and (21) for someT>0. Then there are three positive constantsε1,δ1, andC1, which are independent ofT,γ, andandδ<δ1, it follows that

∀t∈[0,T]

(22)

The local solution(Ψ,Φ,Z) can be extended toT=+∞, provided that Proposition 2.1 is obtained.

With Theorem 2.1, Theorem 1.1 can be proved directly. So our primary mission in the next section is to prove Proposition 2.1.

3 Proof of Proposition 2.1

In this section, the proof of priori estimation is discussed emphatically. ForT>0, it is supposed that expressions (18)-(20) have a solution (Ψ,Φ,Z)∈δ0(0,+∞), then there is

(23)

Based on expression (23), there is

(24)

Expression (24) ensuresvandθhave positive lower bounds on [0,T].

Lemma3.1Under the same assumptions of Proposition 2.1, there are constantsCandεindependent ofT. If

it holds that

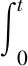
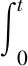
I1(Ψ,Φ,Z)t+I2(Φ,Φx)+I3(Z,Zx)=

(25)

where

By the monotonicity ofvs, there is

(26)

Furthermore, there is

ξx=-σ2(vs)′=σ(U)'

ξt=-σ2(us)′

(27)

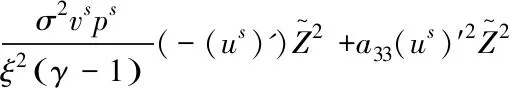
and

(28)

where

Define

To make sureXAXT>0, i.e., the matrixAis positive, the following two conditions should be satisfied:

(29)

whereβ=γ-1. It is clear that (29)2contains(29)1.So if

(30)

and

(31)

From expressions (25) and (28)-(31), there is

(32)

Integrating expression (32) with (0,t)×, recalling the transformationsand takingδ,εthat are sufficiently small, Lemma 3.1 is obtained.

Lemma3.2Under the same assumptions of Proposition 2.1, it follows that

(33)

ProofMultiply (18)2by -vsΨx, using (18)1, the following equation is obtained:

(34)

Integrate expression (34) with respect to (x,t) with×[0,t], there is

(35)

Now, with expressions (19) and (26),I1-I5are estimated term by term:

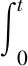
Ifδis sufficiently small, expression (33) is obtained.

zcan be rewritten as

(36)

Square the left and right ends of expression (36). Integrate the result with respect to (x,t)over×[0,t]. The following inequality is obtained:

(37)

Lemma3.3Under the same assumptions of Proposition 2.1, the following inequality holds:

(38)

ProofMultiplying (15)1byχ, (15)2byvsφ/ξ, (15)3byz/ξ2, and adding all the results, there is

(39)

Integrate expression (39) with respect toxandtwith×[0,t]. Using the Young’s inequality, the Sobolev inequality and expressions (16) and (17), it follows that

Lemma3.4Under the same assumptions of Proposition 2.1, there is

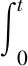
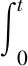
(40)

ProofMultiply (15)2by -vsχx, and integrate the result with respect totandxover [0,t]×. With (15)1, the following equation is obtained:

(41)

With expression (17), there is

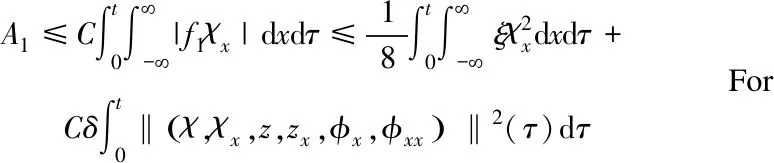
‖χ‖2+‖z‖2+‖zx‖2)(τ)dτ

(42)

Using the above inequalities, by takingδwith small enough value, there is expression (40).

By the same method, the highest-order estimate is obtained. For the sake of simplicity, the proof is omitted.

Lemma3.5Under the same assumptions of Proposition 2.1, it holds that