基于双DQN和扩展卡尔曼滤波的锂离子电池 荷电状态估计

高洪森，王 雪，魏宏博，游国栋，侯晓鑫，赵双乐

(1. 天津力神电池股份有限公司，天津 300384；2. 天津科技大学电子信息与自动化学院，天津 300222)

与铅酸电池以及碱性电池相比，锂离子电池具有能量密度高、自放电率低、无记忆效应以及热效应小等优点[1]．但是，单节锂离子电池只能够产生1.5～4.5V的输出电压，在实际应用中为了获得满足需求的输出电压，通常需要把多个锂离子电池串联起来使用[2]．在电池管理系统(BMS)中，荷电状态(state of charge，SOC)是一个用于表示电池状态的重要参数，它不仅可以给出电池组当前的剩余容量，而且能指示电池组的可用寿命．作为BMS的一个重要参数，SOC一般用于评估电池的运行状态和健康状况[3]，SOC的准确估计对锂离子电池的高效利用和能量管理具有重要意义．

卡尔曼滤波(Kalman filters，KF)算法是利用线性系统状态方程，通过系统输入输出观测数据，对系统进行最优估计的算法．由于观测数据中包括系统中的噪声和干扰，所以也可以把最优估计当作一个滤波过程，卡尔曼滤波算法是一种常见的锂离子电池SOC估计算法[4-5]．锂离子电池在工作时，其运行状态复杂而且容易受很多因素的干扰．为了解决串联锂离子电池组不一致性的辨识与SOC估计等问题，葛云龙等[6]提出一种STF&LM算法，该算法能将各单体电池的SOC、内阻估计误差控制在合理的范围内，从而更好地辨识电池组内电池的不一致性以及进行SOC的估计．范文杰等[7]在分析锂离子电池二阶RC等效电路的基础上，采用电化学阻抗谱对锂离子电池的内部温度进行了估计，该方法提高了电池欧姆电阻和容量估计的精度．上述算法大都把系统的噪声特性设置为已知的量，然而在系统运行时，它的过程噪声方差阵或观测噪声方差阵并不是已知的，并且还具有很强的不确定性和时变性，因此如果错误估计了参数，常常会造成滤波的发散．

深度强化学习将深度学习的感知能力和强化学习的决策能力相结合，可以直接根据输入图像进行输出控制，是一种更加接近人类思维方式的人工智能方法[8-10]．文献[11]利用深度强化学习思维，提出了一种强化学习的锂离子电池SOC估计算法，该方法的优点在于能够更加准确且灵活地估计锂离子电池的SOC，缺点是更改参数存在困难．文献[12]和文献[13]分别将神经网络和卡尔曼滤波算法相结合，提出了两种不同的算法，实验均验证了算法能够提高锂离子电池SOC估计的精度．但是在上述算法中，初始学习参数的选择主要依靠经验，如果参数选择不当，很容易产生局部最优解．廖晓闽等[14]构建了一种深度强化学习的蜂窝网资源分配算法，用于解决蜂窝网资源分配多目标优化问题．作者通过Q-learning机制设计了误差函数，利用梯度下降法训练深度神经网络的权值，训练结果表明该算法能够自主设置资源分配方案的偏重程度，且收敛速度快．

基于上述分析，本文通过构建锂离子电池的二阶RC等效电路模型，建立了离散系统数学模型，设计了一种新的基于深度强化学习扩展卡尔曼滤波锂离子电池SOC估计算法．首先，通过分析锂离子电池二阶RC等效电路模型，建立了电池的SOC空间模型，并利用扩展卡尔曼滤波(extended Kalman filter，EKF)算法构建了锂离子电池的离散系统数学模型．结合人工智能思想，进一步设计了一个深度强化学习扩展卡尔曼滤波锂离子电池SOC估计算法，该算法设计了双深度Q 网络(双DQN，DDQN)，并对EKF参数进行优化．仿真结果表明该算法能够较好 地提高SOC的估计精度．

1 锂离子电池等效电路模型

针对锂离子电池SOC估计的模型主要有等效电路模型、电化学模型和人工神经网络模型．相比后两者，前者能准确表达电池的动态特性，故本文选择锂离子电池二阶RC等效电路模型作为研究对象，锂离子电池二阶RC等效电路模型如图1所示．二阶RC等效电路模型是由两组RC网络、串联的电阻器和电压源组成的电路．图1中：Ut为输出端电压；Uoc为电池开路电压；Rc为电池欧姆电阻；Ic为电池的工作电流；R1、C1分别为电池电化学极化电阻和极化电容；R2、C2分别为电池浓度极化电阻和极化电容；U1为R1、C1的端电压；U2为R2、C2的端电压．

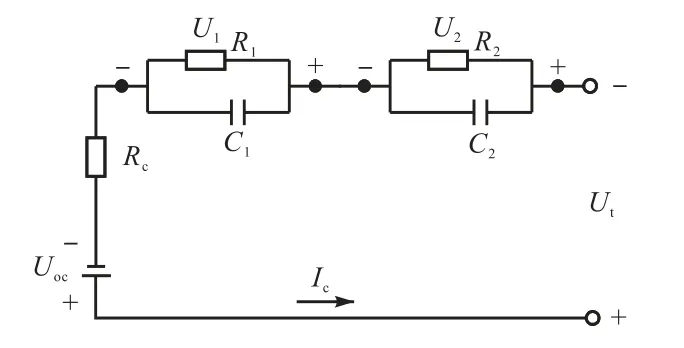
图1 锂离子电池二阶RC等效电路模型 Fig. 1 Second-order RC equivalent circuit model of Liion battery

根据图1的二阶RC等效电路模型可得到电路的基本方程

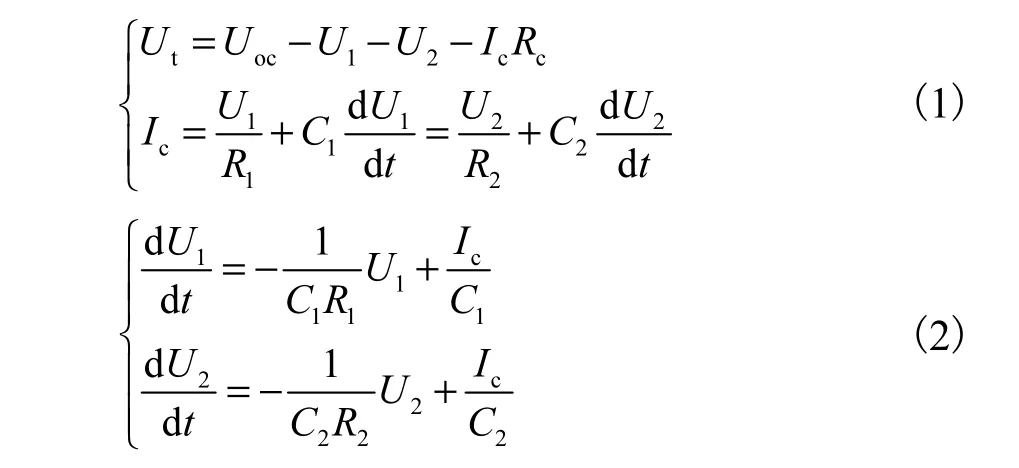
根据美国先进电池联合会的定义，SOC的计算公式为

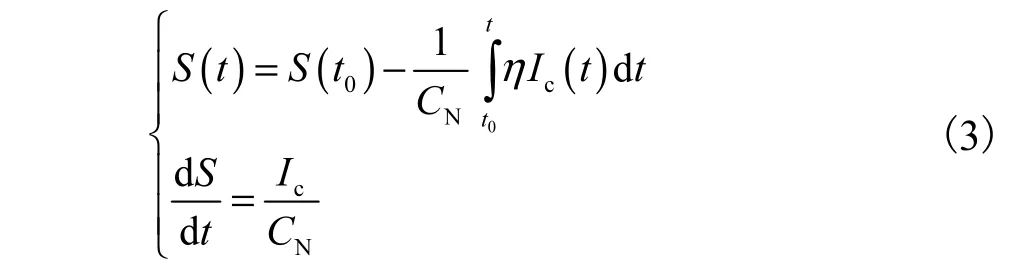
式中：S为电池的SOC；S(t)为t时刻的SOC；S(t0)为t0时刻的SOC；CN为标称容量；η为库仑效率，即实际充电电流与实际电池电流之比．

Ic＞0时，电池正在进行放电；Ic＜0时，电池正在进行充电．

根据开路电压法，可知等效电路模型中的开路电压与电池的SOC存在线性关系．即

2 本文算法

2.1 基本知识

EKF是在KF基础上，将非线性环节线性化，对状态方程和观测方程的系数矩阵进行泰勒级数展开，并忽略或逼近二次及以上的高次项，以此来解决非线性问题．锂离子电池充放电是一种典型的非线性过程，采用EKF对其二阶RC等效电路模型电气基本方程进行离散化，得到

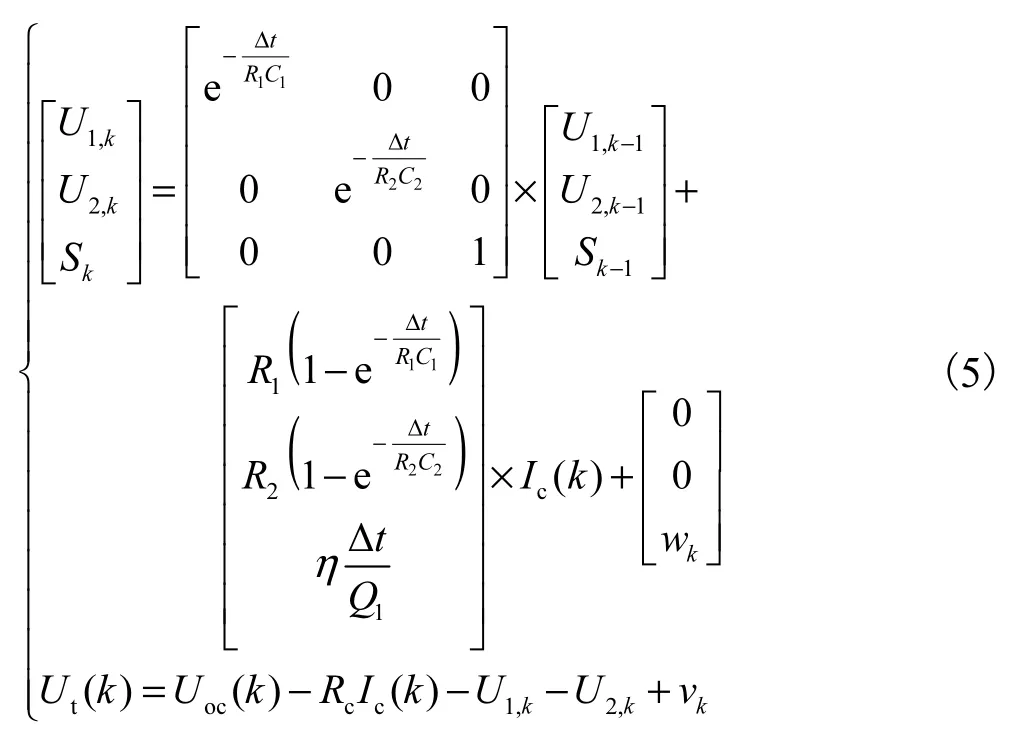
式中：Δt为采样时间，Q1为电池额定容量，wk为系统噪声，vk为观测噪声．

双DQN通过使用两个Q网络解决算法在学习过程中产生的过估计问题[14]．双DQN利用当前Q网络Q(st，at，θ)负责动作的选择，利用目标Q网络Q′(st，at，θ)负责计算目标Q值，减少因为Q值的最大值计算带来的偏差所导致的值函数过估计问题，关系如式(6)所示．

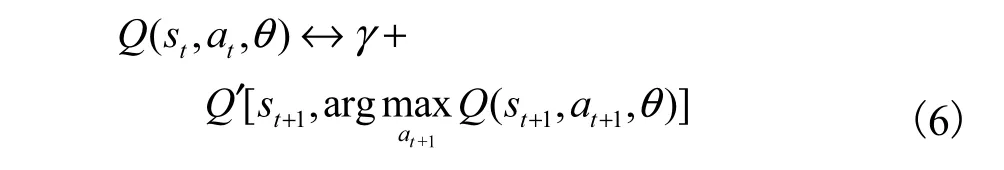
式中：at为当前Q网络选择的动作变量，st为当前Q网络的状态变量，θ为当前Q网络的参数，γ为当前Q网络的折扣因子．

基于双DQN的目标Q值计算如下

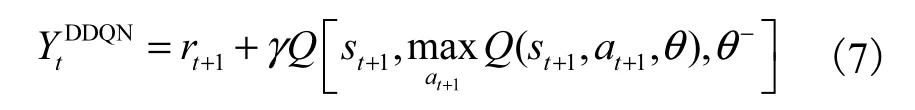
式中：rt+1为目标Q网络的奖励变量；θ-为目标Q网络的参数．

2.2 运行流程

利用控制动作执行的实时情况，对强化学习控制进行优化训练，通过学习对EKF的参数进行持续优化．为了避免学习陷入局部最优，同时保证算法的收敛速度，本文引入了贪婪策略(ε-policy)．在双DQN模块中，通过在每次迭代中优化目标函数，实现损失函数[Yi－Q(si，ai，θ)]2的最小化．优化储能预测的EKF中参数的双DQN流程图如图2所示．

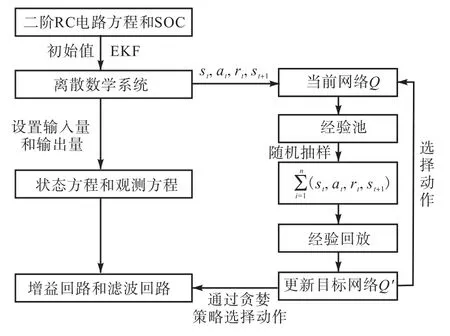
图2 优化储能预测的EKF中参数的双DQN流程图 Fig. 2 Double DQN flow chart for optimizing parameters in EKF for energy storage prediction

基于双DQN和EKF的锂离子电池SOC估计的运行流程由两部分组成，分别为环境和智能体．

第一部分为环境，它由等效电路模块和EKF模块组成．首先，构建锂离子电池二阶RC等效电路模型，建立锂离子电池动态特性电气方程；然后，将电气方程离散化，获得状态方程和观测方程；最后，代入EKF模块中，进行循环迭代，对锂离子电池的SOC进行估计．作为环境，需要为智能体提供状态变量st、动作变量at和奖励变量rt，并且需要对它们的参数进行设置．

状态变量类型的选择对控制性能有重要影响. 为了防止训练后的深度神经网络陷入局部最优，一般需要观察和训练的状态变量较少．然而，双DQN算法在缺少关键状态变量的情况下，可能无法充分理解状态转换过程与环境之间的相互作用关系，导致迭代和收敛困难．因此，选取等效电路模型的状态函数和EKF中导致SOC估计造成误差的函数作为状态变量，即

由于所研究的锂离子电池二阶RC等效电路已通过EKF转换为离散数学系统，需要将动作离散化，并且将离散化步长设置适中．如果离散化步长过小，则增加算法训练时间；如果离散化步长过大，会造成算法的局部最优．根据假设，EKF为双DQN模块提供EKF中的观测方差R，动作参数为

Action＝{increasing R 10 times，increasing R 5 times，maintaining R，decreasing R 5 times，decreasing R 10 times}

奖励函数用于评估给定状态下动作值的质量，主要依赖于SOC的估计误差(eSOC)，其定义为

式中：Re表示奖励函数，Lr表示学习因子．

第二部分为智能体，即双DQN模块，它利用由EKF模块提供的状态st、动作at和奖励rt，采用贪婪策略选择动作，改变EKF中的观测方差R，将产生的经验样本(rt，st＋1)存储到经验池中，然后每隔D步对随机抽取的经验样本进行经验回放，更新网络参数．该部分的核心是采用贪婪策略选择动作对EKF模块的参数进行优化，随着迭代次数的增加，动作的输出逐渐稳定，奖励函数获得最优值．该模块的算法框架如图3所示．

图3 双DQN模块的训练算法框架 Fig. 3 Training algorithm framework of double DQN

根据仿真需求与人工经验对双DQN算法的超参数进行设置．超参数是在算法开始学习过程之前设置的参数，包括学习率α、折扣因子γ、存储样本最大值N、贪婪策略的初始概率ε和经验回放大小n，超参数设置见表1．

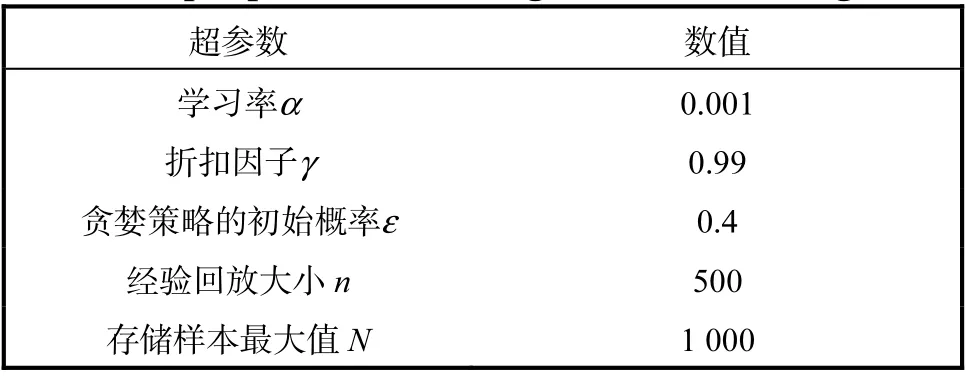
表1 双DQN算法的超参数设置 Tab. 1 Super parameters setting of double DQN algorithm

3 仿真实验

3.1 参数设置

3.1.1 电池基本参数

文中选取的研究对象为天津力神电池股份有限公司生产的18650EC型锂离子电池，该电池的额定容量为1.3A·h，标称电压为3.2V，充电截止电压为3.6V，放电截止电压为2.8V．

3.1.2 测量步骤

使用电池测量装置，不断地进行充放电实验，测量电池的开路电压，测量时按照如下步骤进行操作：

第一步：将待测电池测试环境的温度设定在常温(20～25℃)．

第二步：0.02It(It为参考电流)恒流充电至3.6V，然后恒压充电，至电流小于0.02It，静置1h．SOC标记为100%，记录放电开路电压．

第三步：0.02It恒流放电，放电时间为10min，静置1h．SOC标记为90%，记录放电开路电压．

第四步：重复第三步，分别将电池的SOC标记为80%、70%……10%、0．

第五步：静置1h，0.02It恒流充电，操作过程与放电过程相同，每次充电后静置1h，记录充电开路电压．

3.1.3 拟合Uoc-S特性曲线

经过以上的测量步骤，可以得到电池不同SOC时对应的开路电压，拟合后得到的Uoc-S特性曲线如图4所示．

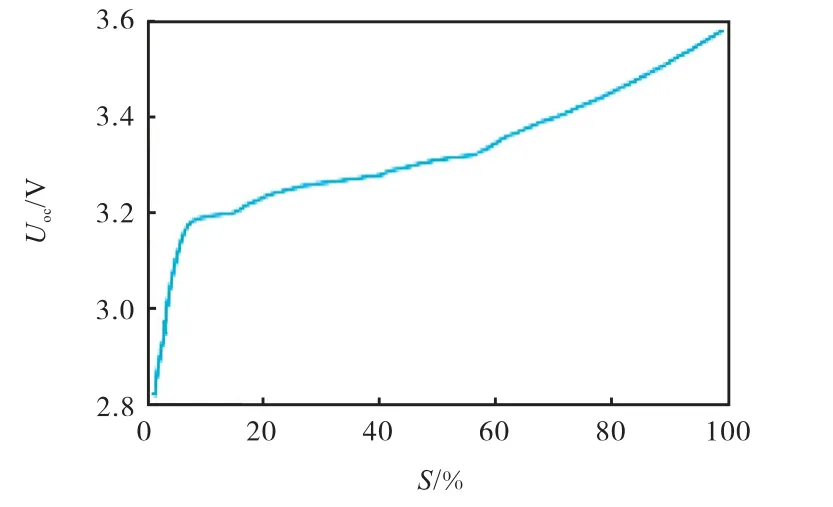
图4 Uoc-S特性曲线 Fig. 4 Uoc-S characteristic curve

3.2 仿真

基于DQN和双DQN算法的训练迭代中累计奖励的均值如图5所示．在学习的初始阶段，智能体更倾向于选择“探索”策略，目的是找到更多有关环境的信息(即尝试各种控制动作)，导致累计奖励的均值在相对较低的水平．随着训练迭代的进行，两种智能体都逐渐倾向于选择累计奖励较高的动作，即奖励函数值随着SOC的估计误差的减小而单调增加，最终趋于稳定．但由于探索的波动，累计奖励并不是严格连续递增的．与DQN相比，基于双DQN的策略在收敛速度上显示出更好的性能和更高的累计奖励的均值，表明双DQN可以同时产生更准确的价值估计和更好的策略．

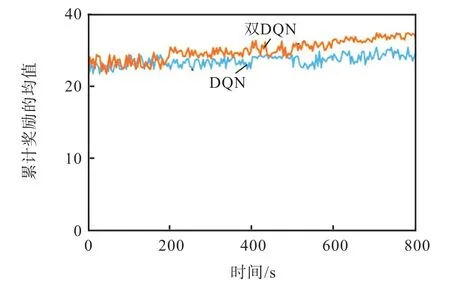
图5 累计奖励的均值 Fig. 5 Average value of cumulative awards

基于EKF的锂离子电池SOC的估计误差观测图如图6所示．在仿真初始阶段，误差较小；但是，随着时间的推移，误差逐渐变大，最后逐渐变小，趋于平稳．基于EKF的锂离子电池SOC估计虽然具有较好的准确度，但是仍旧存在误差偏大和收敛时间较长的缺点．

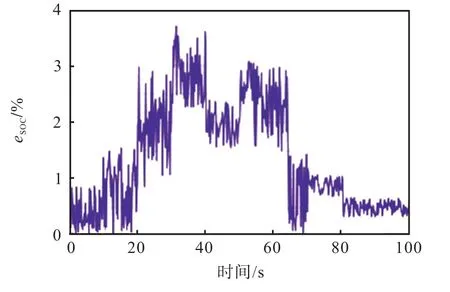
图6 基于EKF的锂离子电池SOC的估计误差观测图 Fig. 6 Observation diagram of state of charge estimation error of Li-ion battery based on EKF parameters

基于DQN和双DQN算法优化EKF参数的锂离子电池SOC的估计误差观测图如图7所示．在仿真初期，基于DQN和双DQN算法的SOC的估计误差均偏大；但是随着迭代训练的增加，两者SOC的估计误差均逐渐变小．对比图5—图7可知，双DQN算法得到的锂离子电池SOC的估计误差比另外两种算法得到的要小，双DQN算法的性能高于另外两种算法．

图7 基于DQN和双DQN算法优化EKF参数的锂离子电池SOC的估计误差观测图 Fig. 7 Observation diagram of state of charge estimation error of Li-ion battery based on DQN and double DQN algorithm to optimize EKF parameters

4 结 语

针对锂离子电池的SOC估计精度问题，结合传统的EKF算法和深度强化学习思想，设计一种新的双DQN扩展卡尔曼滤波锂离子电池SOC估计方法．该方法采用深度强化学习对EKF的参数进行优化，对原有的SOC估计方法进行改进，提高了SOC的估计性能．通过实验测试与数据拟合，构建锂离子电池开路电压与SOC特性曲线模型，设计关于优化储能预测的EKF中参数的双DQN的框架图，选择等效电路模型的状态函数和EKF中导致SOC估计产生误差的函数作为状态变量，对控制动作EKF中的观测方差进行改变，从而对SOC进行估计．仿真结果表明，该估计方法在利用两种算法优点的基础上，有效降低了估计过程的计算量，进而提升了SOC估计的精度，具有较好的实用性．