芳纶短纤维增强橡胶复合材料界面力学性能表征及有限元模拟

刘霞，杨晓翔,高剑虹

(1.福州大学机械工程及自动化学院，福建 福州 350108；2.泉州师范学院化工与材料学院，福建 泉州 362000)

0 引言

短纤维增强橡胶材料的应用领域广泛，因其力学性能好、来源易获取、轻量化等优点逐渐成为传统材料的替代品[1]，材料性能的精确预测为复合材料的安全使用提供了保障.由于细观层面下的界面性能无法直接测量，建立细观结构和复合材料宏观力学性能之间的联系显得格外重要[2].

从短纤维增强复合材料的断裂实验来看[3]，界面并非完全粘结：基体发生横向断裂、纤维从基体中拔出.在纤维与基体之间引入损伤模型能模拟纤维与基体之间的脱粘.界面损伤模型在细观层面预测材料的损伤过程和力学性能得到了广泛的应用[4-7].沈珉等[8]基于双线性内聚力模型建立随机植物短纤维复合材料二维代表体积单元，并研究了界面性能对有效弹性模量和拉伸行为的影响.段宇星等[9]基于剪滞理论建立短纤维增强橡胶材料的理论和数值模型，并对短纤维增强阻尼材料的弹性模型进行计算与拟合.

现阶段，对纤维增强橡胶复合材料的性能探索以建立二维平面模型较主流，有限元技术的发展使建立复杂的细观结构力学模型成为可能.Vaughan等[10-11]提出一种二维单胞复合材料模型建立的新算法，代表体积单元(representative volume element,RVE)单胞模型能保证纤维之间的分布距离跟实际细观吻合.Qi等[12]基于Python-ABAQUS提出一种改进的随机序列吸附算法(random sequence adsorption algorithm,RSA)来生成纤维，研究了具有一定长径比的空间随机分布短圆柱纤维增强复合材料的有效弹性性能.Ge等[13]提出一种基于迭代改进的生成高纤维体积分数(高达70%)随机分布连续纤维增强复合材料细观结构的新方法，克服了传统随机序列吸附法的干扰限制.该算法计算效率高，纤维生成随机性好，但其RVE局限于二维平面且没有考虑界面损伤.

本研究采用数值仿真/实验相结合的方法，研究芳纶短纤维增强橡胶复合材料拉伸力学性能.基于Python-ABAQUS二次开发，建立含损伤界面的随机纤维分布二维代表体积单元，采用cohesive单元表征界面性能，通过编写的Python脚本程序对模型自动施加周期性边界条件.最后通过ABAQUS模拟仿真RVE对拉伸载荷的力学响应，分析不同界面参数以及纤维含量对芳纶短纤维增强橡胶复合材料(aramid fiber-reinforced rubber composite,AFRC)轴向拉伸力学性能的影响.

1 实验设计及过程

由于芳纶纤维高强度和高模量等优异的力学性能，在橡胶基体中少量加入即可提高制品的整体性能.为考察复合材料的宏观力学性能，分别采用Kevlar对位芳纶短切纤维制备了4种配方的AFRC，见表1.表中配方代号F表示无添加纤维的橡胶基体，K表示添加Kevlar对位芳纶纤维.文中研究的Kevlar纤维长度为l=1.5 mm，试件中芳纶纤维的质量份数从1份增加到7份，而橡胶基体、炭黑和其余配合剂的掺加量均相同.实验炼胶分二段混炼，分别在密炼机和开炼机上进行，各段混炼胶料停放时间不少于8 h，在平板硫化机上进行硫化，硫化温度为143 ℃，时间为45 min.

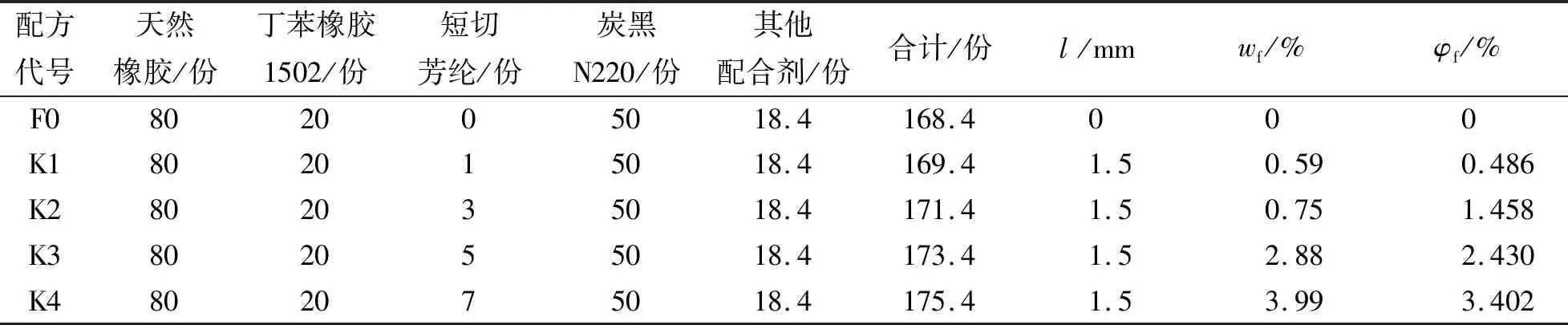
表1 芳纶纤维增强橡胶复合材料配方Tab.1 Formula of aramid fiber-reinforced rubber composite

由于芳纶纤维的投放是无序且不定向的，在胶料中的分布并不完全呈现沿轴向分布[14].拉伸试样所用的裁刀和裁片机符合国标GB/T2941[15]的要求，所制备的橡胶尺寸参考国家标准《硫化橡胶或热塑性橡胶拉伸应力应变性能的测定》(GB/T528-2009[16])中“I型”哑铃状试样的要求(如图1所示).采用日本岛津公司研发的AG-X plus岛津电子万能试验机，在常温(23 ℃)对哑铃形试件进行单向拉伸.

图1 I型哑铃形状试件形状和尺寸(单位：mm)Fig.1 Shape and size of I-shaped dumbbell specimen (unit:mm)

采用1 mm·min-1的拉伸速率，对试件进行准静态单轴拉伸实验，结果见图2.图2中列出了纤维体积分数为0.486%、1.458%、2.430%和3.402%试件的实验拉伸应力-应变曲线和将纤维/基体界面看作是理想粘结界面的有限元仿真应力-应变曲线.从图2中可以看出，纤维体积含量对AFRC的拉伸应力-应变曲线有一定的影响，体现在纤维体积含量越高，同应变条件下AFRC的真实应力越高.K1试件的应力-应变曲线位置与K2试件基本重合，而K4的应力-应变曲线的位置较K2有明显的变化，验证了在一定的纤维含量范围内，纤维含量的增加对AFRC的增强效果明显，而对于小含量的纤维对AFRC的增强作用变化较微弱.

图2 K系列试件受单轴拉伸载荷时的应力-应变曲线Fig.2 Stress-strain curve of K series specimen under uniaxial tensile load

2 有限元模型的建立

2.1 RVE单胞模型建立

复合材料在细观层面的力学响应特性可反映其在宏观层面的有效性能[17].复合材料在细观层面并不是完全均匀的，但是纤维在复合材料的分布具有一定规律性，在统计学上称其为周期性随机分布，将包含足够多的信息又能独立代表复合材料的RVE扩展排布即可构成复合材料的整体结构.RVE是整体结构中具有代表的一部分，有些纤维部分在建模时难以避免会超出RVE的边界，则需要将超出部分切割后，将其平移至对应边的RVE内部[18].

采用Python语言编程建立二维短纤维随机分布代表体积单元(RVE)模型.考虑芳纶纤维的体积含量、纤维的随机位置分布以及纤维的大长径比特性等细观结构信息.程序编写分为如下步骤：

1) 建立力学简化模型，创建二维基体，其大小与RVE大小一致，并在该基体中创建第一根纤维.

2) 两次调用Random函数分别完成对第一根纤维的平面旋转和平面平移得到第二根纤维.

3) 利用判断语句对投放纤维体积分数的判断，未满足设定纤维体积分数的投放时，则继续投放纤维，直到达到设定参数.

4) 输出模型.为了保证周期性边界条件的顺利自动实施，需要在RVE的对边保证网格的一致性，这步可通过网格的复制得到保证.通过Python编写的程序可获得互不干涉的随机分布纤维，建立随机分布纤维增强橡胶复合材料的代表体积单元，模拟研究AFRC的单轴拉伸力学性能.建立了纤维体积分数为0.486%、1.458%、2.430%和3.402%的二维RVE模型，其中，纤维含量为3.402% AFRC的RVE有限元模型如图3所示.针对本研究所建立的有限元模型，橡胶基体和芳纶纤维采用线性减缩积分单元(CPS4R)；为保有限元模型能容纳足够多的纤维，模型尺寸取6 mm × 6 mm.

图3 纤维含量为3.402% AFRC的有限元二维数值模型Fig.3 Two-dimensional finite element model of AFRC with 3.402% fiber

2.2 材料参数及界面表征

将随机芳纶纤维增强橡胶复合材料的纤维/基体界面看作是非理想界面.双线性内聚力模型能很好地描述应力和位移的非线性关系(如图4所示)，可用来表征AFRC的非理想界面.从图2可以看出，采用理想界面(界面不发生脱粘)模拟材料的力学性能与真实的应力应变曲线有一定的偏差.利用ABAQUS软件建立的RVE模型中，采用零厚度二维四节点cohesive单元(COH2D4)表征纤维与基体之间的非理想界面力学行为，界面单元的本构模型遵循双线性内聚力模型，认为纤维与基体之间的界面性能皆相同，即界面单元的本构模型参数皆相同，有σmax=τmax，δ1=δ1n=δ1s，δd=δdn=δds.在模拟过程中基体与纤维不发生断裂，模型仅在纤维与基体之间的界面发生破坏.

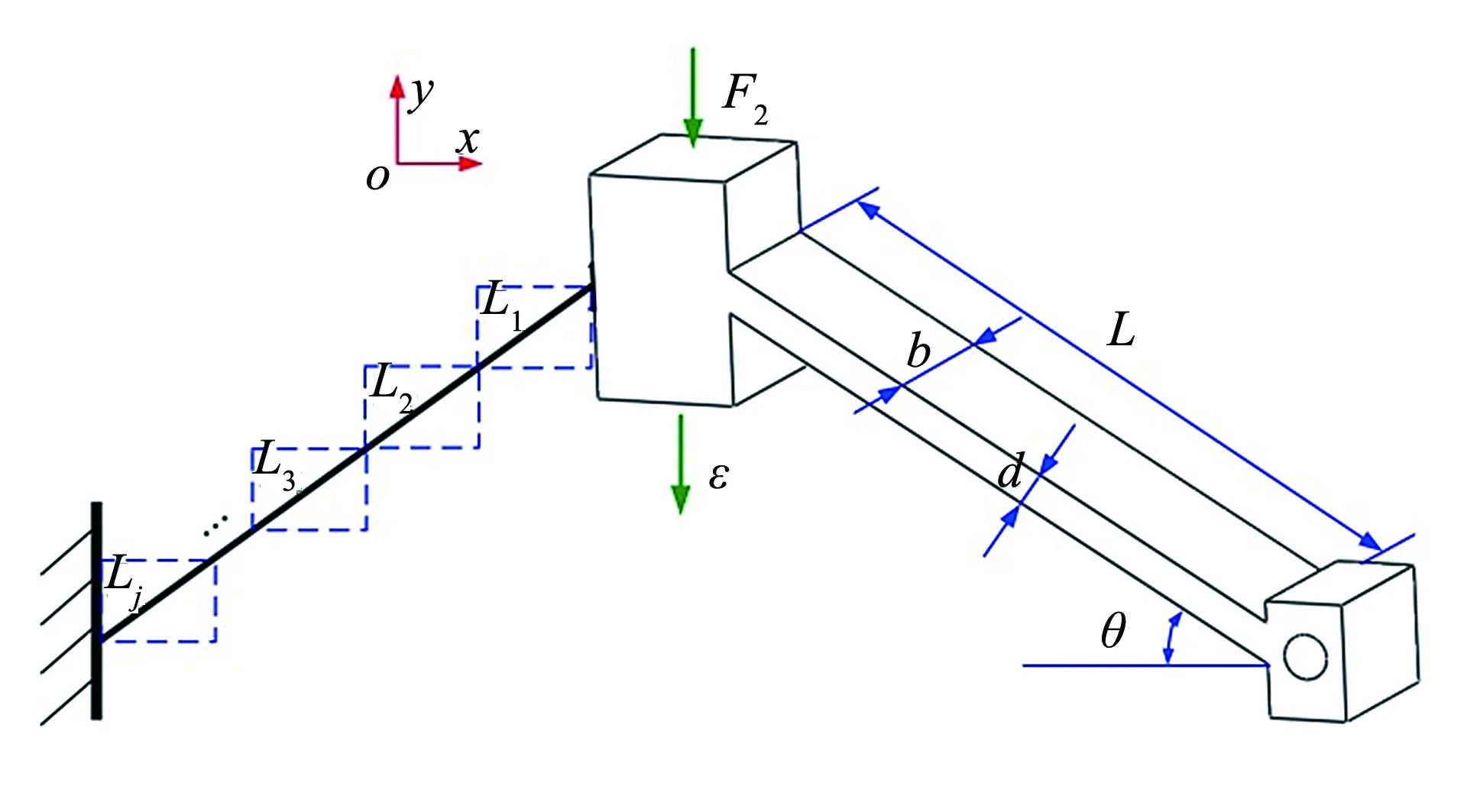
图4 界面的双线性内聚力模型Fig.4 Elastic-softening cohesive zone model for the interface

界面单元处于线弹性阶段(0≤δ≤δ1)，应力随着分离位移增大而增大.当界面应力达到损伤初始准则后，界面损伤开始.采用的内聚力单元的初始损伤判据如下：

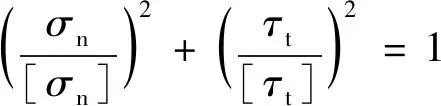
(1)

式中：σn和τt分别是界面的法向应力和切向应力；[σn]和[τt]分别是界面的法向脱粘强度和切向脱粘强度.

界面进入损伤演化阶段(δ1≤δ≤δd)，应力随着分离位移增大而减小，直至为零，此时界面完全失效.界面损伤参数(scalar stiffness degradation,SDEG)可描述为界面损伤程度，损伤参数SDEG可表示为:

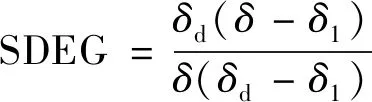
(2)

式中：δ为损伤过程中界面的最大分离位移.

芳纶纤维可视为各向同性弹性材料，其弹性模量为70 GPa，泊松比为0.3.纤维在基体材料的分布位置是随机且不定向的.

基体是均匀各向同性的超弹性材料.根据唯象理论，橡胶类材料的应变能函数W是右柯西-格林变形张量C=FTF的函数，即:

W=W(C)=W(I1，I2，I3)

(3)

式中：F=∂x/∂X为变形梯度;x和X分别为欧拉构型与拉格朗日构型中的位移矢量；Ii为应变不变量.

采用经典的超弹性本构模型Ogden N3[19]描述橡胶基体的应力-应变行为，Ogden N3模型可表示为:

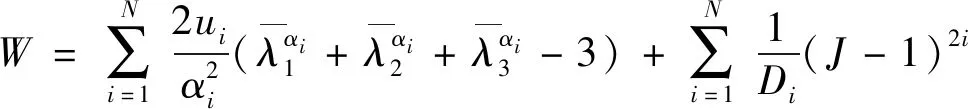
(4)

利用ABAQUS有限元软件中的材料参数回归模块，得到表1中F0无纤维试件的材料参数如下:μ1=8.116 MPa，α1=1.975，μ2=5.725 MPa，α2=2.388，μ3=5.467 MPa，α3=4.495.由于纤维的面内分布特点，假设二维数值模型为平面应力问题.

2.3 周期性边界条件的建立

对细观有限元模型合理施加边界条件有利于获得准确的细观力学响应.周期性边界条件的实施必须满足对应边界面的应力连续和位移连续[20].AFRC的二维RVE几何表述见图5，对RVE模型施加周期性边界条件，在相对平行的两个对面上以及在各个顶点满足：

图5 AFRC的二维RVE几何表述Fig.5 Geometrical frame of two-dimentional RVE for AFRC

ul2=ul1+(uA1-uA0);ul4=ul3+(uA2-uA0)

(5)

式中：u表示边界上节点的位移向量；下标l1，l2，l3，l4代表4条边；A0，A1，A2，A3代表4个角点.

基于周期性边界条件理论与ABAQUS二次开发程序的编写规则，编写对有限元模型自动添加周期性边界的脚本，并通过“equation”实现式(5)在ABAQUS的用户界面的自动运行.约束A0点在x和y的位移，约束A1点在y的位移，约束A2点在x的位移，并通过在A2点施加y向位移载荷以实现对代表体积单元的单向拉伸模拟.

3 有限元分析

通过RVE模型可计算不同纤维体积含量的AFRC应力应变曲线，其中AFRC的真实应力由加载方向的约束反力除以变形后的表面积计算得到，真实应变ε的计算公式为：

(6)

式中：u为加载施加的位移值；L为RVE的边长.

通过式(7)可以计算得到AFRC在单向拉伸时的应力应变曲线.通过取曲线在0.002应变下的正切模量来近似AFRC的有效弹性模量E[21].

3.1 网格密度对有效弹性模量的影响

对于体积分数为4.302%的RVE几何模型建立了不同的网格密度，图6给出了AFRC的有效弹性模量与单元网格密度的关系图.从图6中的试算结果可以看出，随着网格密度的增加，有效弹性模量的值逐渐趋于平缓，这说明在一定合适范围内的网格密度条件下，网格密度对仿真的结果没有影响.考虑计算机的计算时长和计算收敛性，网格密度不宜过细.在网格密度大于132 × 132时材料的有效弹性模量时预测偏差小于5%，所以本研究在建立RVE模型时，其网格密度取值为132 × 132，基体单元对应的尺寸为0.055 mm.对于芳纶纤维这种大长径比且直径非常微小的材料，在仿真时需保证结果的收敛性，需要在纤维与基体连接处进行网格的细化来保证计算结果的收敛性.

图6 网格密度对AFRC宏观有效弹性模量的影响Fig.6 Effect of mesh density on the macroscopic effective modulus

3.2 内聚力模型参数对AFRC应力应变曲线的影响

图7中给出不同界面刚度K、不同初始裂纹产生位移δ1、不同完全破坏位移δd下内聚力模型的5组界面模型数据.分别应用到数值模型中进行有限元仿真，得到了纤维体积含量为3.402%的AFRC的界面参数对应力应变曲线的影响，如图8所示.

图7 内聚力模型参数Fig.7 Parameters of cohesive zone model

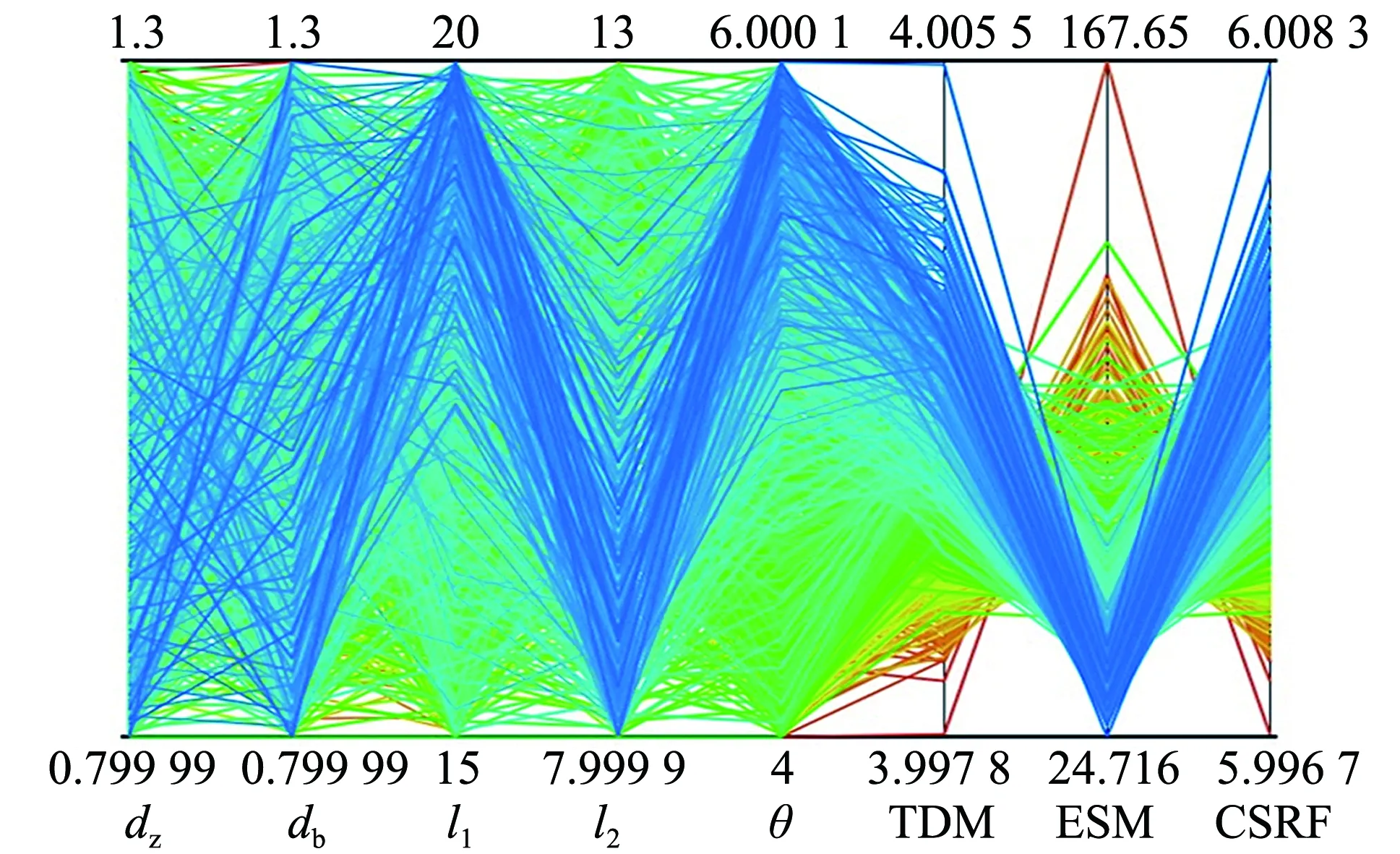
图8 界面参数对有效弹性模量的影响Fig.8 Influence of interface parameters on effective modulus

对比S1和S2，在K和δd取值相同、δ1取值不同的情况下，可以看出界面的断裂能(即曲线与横轴所围的面积)对应力应变曲线有很大的影响，着重体现在大断裂能导致曲线在初始弹性阶段非线性特征不明显，表现为需要大应力才能使曲线进入非线性阶段.S1的δ1较大，对应拉伸曲线的最大应力也越大.

对比S3和S4，在断裂能相同的情况下，S3的界面刚度比S4的界面刚度要大，在应力应变曲线中，S3曲线在初始阶段的斜率未与S4重合，界面刚度小则对应的应力应变曲线的斜率小，反映材料在弹性阶段的有效弹性模量小，可以说明界面刚度对复合材料的有效弹性模量的估计有一定的影响.

对比S2和S3，保证其他参数不变，只改变界面的δd，在完全失效位移增大一倍的情况下，曲线在非线性阶段两者没有明显的分离.特别地，S2和S3有相同的界面刚度值，两者对应的应力应变曲线在线性阶段是重合的，可以推断界面刚度相同的复合材料其有效弹性模量相同.

综上所述，以及对比S1、S3和S5，推断出内聚力模型的界面刚度K只影响曲线的线性阶段，对于材料在非线性阶段的影响取决于δ1、δd的值.

3.3 界面刚度对AFRC弹性模量的影响

为了研究界面性质对AFRC轴向拉伸性能的影响，模拟相应体积含量的AFRC的拉伸力学行为，选取20～1×106MPa·mm-1之间共15个不同界面刚度值，计算每个界面刚度值所对应的有效弹性模量.图9给出4种纤维体积分数对应的不同界面刚度下的AFRC轴向拉伸的界面刚度-弹性模量曲线，可以看出，界面刚度对AFRC的有效弹性模量有很大的影响.选取合适的界面刚度对预测AFRC的力学性能有很大的影响.同时，界面刚度的增大使得AFRC的有效弹性模量增大.

图9 AFRC的刚度-弹性模量曲线Fig.9 E-K curves of AFRC

在同一体积含量下AFRC的有效弹性模量随着界面刚度的提高，AFRC的轴向拉伸模量有所提高，说明界面刚度对AFRC轴向拉伸有效性能有一定的影响.界面刚度值较大时，可看作是界面的理想粘结情况下，界面刚度值趋近于无穷大，曲线呈现水平稳定值.对于曲线在小界面刚度下，曲线呈现非线性特性，且呈现随着界面刚度的增大，材料的有效弹性模量也增加.由此可以推断，界面刚度和宏观有效性能之间有单调递增的关系.

3.4 纤维体积含量对AFRC弹性模量的影响

从图9中可以看出，不同体积分数的曲线皆在一点聚集后分散.将聚集的一点称为临界交点，把临界交点对应AFRC的有效弹性模量称为临界有效弹性模量.在本研究所制备的AFRC的临界界面刚度，按照图9中曲线拟合计算为50 MPa·mm-1.不同的复合材料的加工工艺所对应的临界界面刚度不同，可以推断对纤维与基体之间的界面进行处理可提高材料的有效性能.

在临界交点的弱界面刚度区域，即非理想界面的刚度小于临界交点值，随着纤维体积分数的增加有效弹性模量减小，即小含量纤维对AFRC的增强作用较小.在强界面刚度区域，即非理想界面的刚度大于临界交点值，纤维体积含量的增大会增加材料的有效弹性模量.但是界面的增加作用不是无限增加的，当界面刚度超过一定值，材料的有效弹性模量会趋于水平线，这种情况下AFRC的界面可看做是理想粘结.根据图2模拟的理想粘结情况下的应力应变曲线，在仿真中将界面处假设成理想粘结对预测的有效弹性模量以及模拟曲线的应力应变曲线有一定的偏差.

对于纤维含量为0.486%的AFRC，界面刚度对有效弹性模量的影响小，强界面刚度区域对材料的有效弹性模量的增强作用较弱界面区域仅增加27.12%.芳纶的大长径比特性使得纤维在轴向受力能传递应力，但是由于芳纶的直径小，使得小含量的纤维比大含量的纤维所承受的受力面积少.界面刚度特性反映了一定的界面粘结程度，小含量纤维相比大含量纤维在界面处承受应力传递的作用范围少.图9中纤维含量为1.458%的AFRC有效弹性模量在界面刚度范围内增加了86.63%.同样地，纤维含量为2.430%和3.402%的AFRC有效弹性模量在界面刚度范围分别增加了192.07%和385.35%.特别地，临界交点的存在可以说明在进行复合材料的加工工艺中要规避弱界面刚度区域.通过对纤维表面的化学处理[22]或物理粘附[23]改善纤维与基体之间的浸润性；或使用偶联剂[24]可增加宏观复合材料的有效弹性模量.

3.5 界面参数的确定

由实验给出的纤维含量为0.486%、1.458%、2.430%和3.402%四种不同体积分数下的材料的应力应变曲线，可以得到其宏观有效弹性模量，在刚度-弹性模量曲线上可找到对应界面刚度的数值，实验测得的有效弹性模量在图9用空心点表示.AFRC的有效弹性模量值唯一确定该材料的界面刚度值.

第3.2小节分析了界面参数对材料应力应变曲线的影响，说明界面刚度只影响应力应变曲线在弹性阶段的斜率，通过求解实验应力应变曲线中的有效弹性模量与图9的刚度-弹性模量曲线比对，可确定在纤维含量、纤维尺寸、纤维随机分布状态都跟有限元模型相同情况下的AFRC的界面刚度的具体值.再调试ABAQUS中δ1的值，得到一组应力应变的仿真曲线，与实验的应力应变曲线进行对比，找到形状吻合实验曲线的初始裂纹位移δ1；再调试δd的值，直到找到吻合实验应力应变曲线在非线性阶段的最终裂纹脱粘位移δd.

拟合曲线在弹性阶段很好地贴近实验曲线后，通过模拟应力应变曲线可以在非线弹性阶段确定δ1和δd的值.S5组的结果表明在确定K后，δ1和δd对曲线的影响较小.可通过拟合曲线在线性阶段的最大值与实验曲线的契合程度确定δ1的值.S2和S3组指出拟合曲线与实验曲线在非线性阶段的形状拟合有一定的关系.可通过拟合曲线与实验曲线的贴合程度确定δd的值.同样地，采用本文相同的方法可确定纤维体积含量为0.486%、1.458%、2.430%的AFRC界面CZM模型的参数，其具体参数如表2.通过表2预估出的具体的界面刚度K、初始裂纹产生位移δ1和最终失效位移δd,可模拟在同等纤维含量下、纤维分布随机、纤维尺寸以及相同加工工艺下的AFRC的其他力学性能.

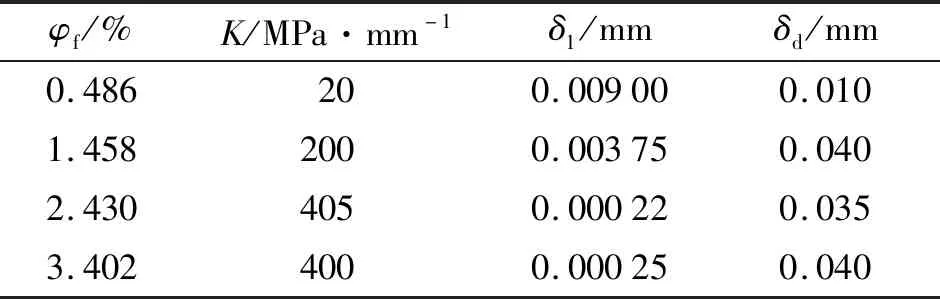
表2 材料界面的内聚力模型参数确定Tab.2 Cohesive zone model parameter determination of material interface

图10给出4种不同纤维含量通过内聚力模型表征非理想界面有限元仿真和实验得到的应力应变曲线.在同一应变条件下，图10中仿真与实验曲线的应力值偏差最大不超过5%，可以认为，利用ABAQUS软件仿真得到的4种不同纤维含量的材料的应力应变曲线能很好地跟实验曲线拟合.

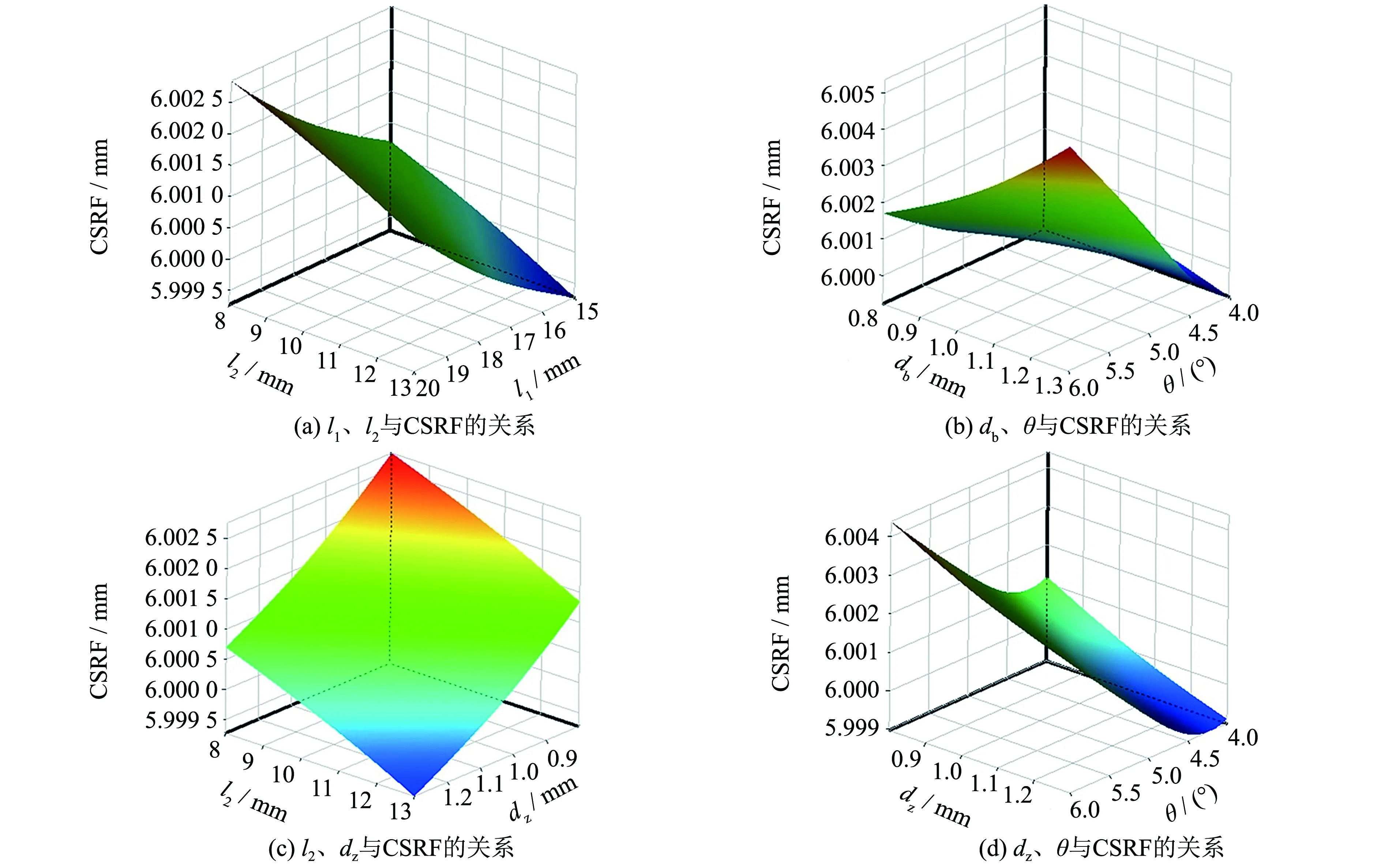
图10 应力应变曲线仿真与实验结果对比Fig.10 Comparison of stress-strain curve values and experimental results

4 结语

1) 建立了随机纤维分布的二维代表体积单元有限元模型，在满足纤维随机分布的同时还能保证各纤维之间互不干涉，添加周期性边界条件的数值模型能更符合真实材料.

2) 通过对AFRC的非理想界面参数的研究表明，有效弹性模量与界面刚度有单调递增的关系，即随着界面刚度的提高，AFRC的有效弹性模量增加.在一定纤维体积含量范围内，纤维体积含量对材料有效弹性模量的增加是有条件的：在弱界面刚度区域，纤维体积含量的增加会导致AFRC有效弹性模量的降低；在强界面刚度区域，纤维体积含量的增加使得AFRC有效弹性模量增加.

3) 通过预估的界面刚度K，初始裂纹位移δ1，最终失效位移δd等界面参数模拟得到的应力应变曲线，与纤维含量0.486%、1.458%、2.430%和3.402% AFRC的实验应力应变曲线吻合.