基于区域离散化的无源雷达布站优化方案
2022-08-30陈宏烨赫志达
陈宏烨,赫志达
(中国人民解放军91550部队,辽宁 大连116023)
0 引言
无源雷达组网对空间目标的测量精度,会随着雷达布站几何变化,而出现较大差异[1]。通常取测量精度最高的布站方案,称为最优布站,该布站方案的精度几何因子GDOP(geometrical dilution of precision)值最小[2]。同时,由于空间目标的位置时刻变化,跟踪测量几何不断变化,导致GDOP值也起伏波动,继而任何布站方案都不可能确保空间目标的全航迹都为最佳几何[3-4]。当前,国内常用距离与距离变化率和时差定位法[1-3]对空间目标进行定位,但目前工程实践中,布站受制约情况较多,因此很难达到最佳几何布站。针对无源雷达的特性和工程实践问题,本文将布站区域离散化,并建立雷达遮蔽算法模型,运用遗传算法,解决空间目标跟踪定位中的无源雷达优化布站的问题。
1 无源雷达定位原理及模型建立
1.1 时差定位建模
时差定位的原理是记录4个无源雷达站采集到的信号到达时间,通过数学解析,最终对空间目标进行定位。设无源雷达组网由1个主站及n个副站构成,其布站几何关系如图1所示。
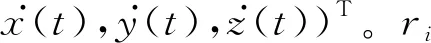
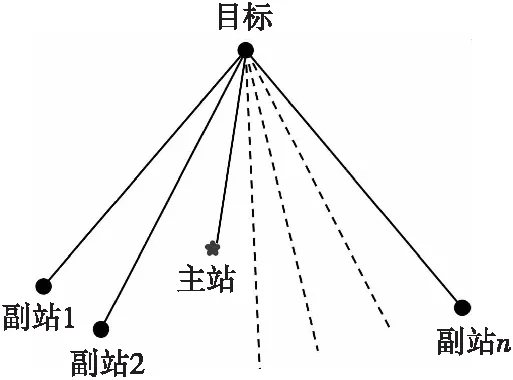
图1 布站几何示意图Fig.1 Schematic diagram of station geometry
则有
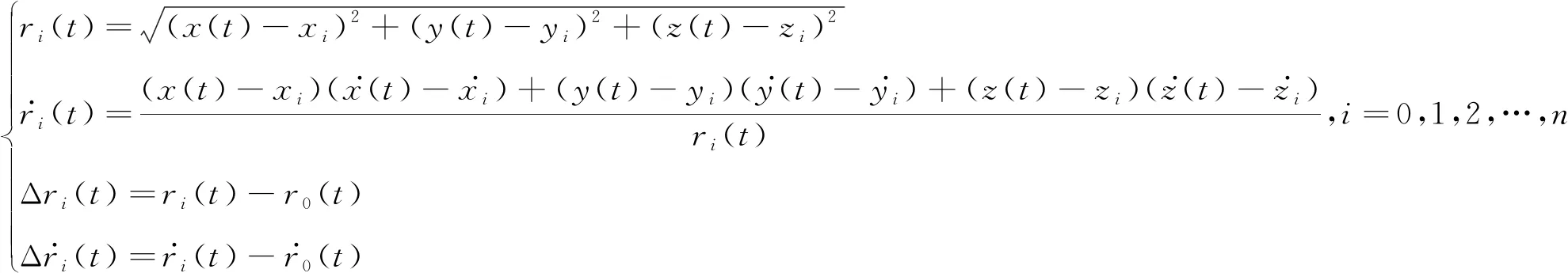
(1)
假定在每一时刻t,获得包括距离和距离变化率在内的6个观测数据,如下式表示:
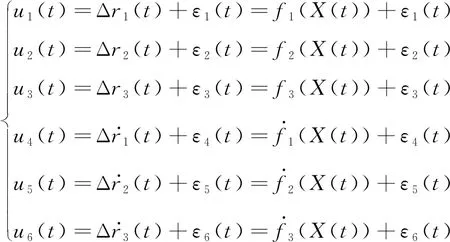
(2)
式(2)观测模型对应的矩阵表示为:

(3)
上述内容表示3个无源雷达站在同一时刻空间上的数据融合。实际应用中,由于空间目标飞行航迹的时间连续性,可用三次标准B样条来表示空间目标的飞行航迹,实现时间上的数据融合。此时,令
(4)
式(4)中,Ti=T2+(i-2)h,i=1,2,…,N;
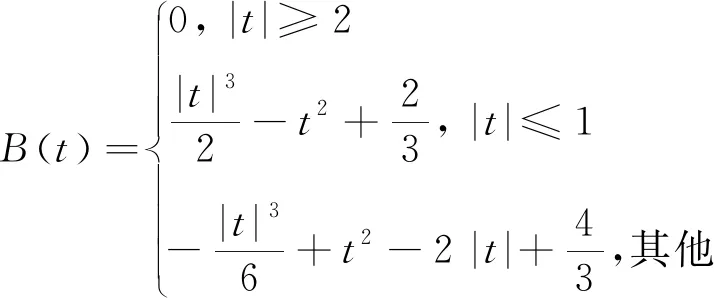
将式(4)代入式(3)可得
U(t)=F(t,β)+ε(t),
(5)
式(5)中,β=(a1,a2,…,a3N)T。此时,我们把关于空间目标飞行航迹的估计转换为对样条函数表示模型参数的估计,建立测量数据U与航迹参数样条系数β之间的非线性回归模型
U=F(β)+ε,ε~N(0,Q)。
(6)
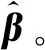
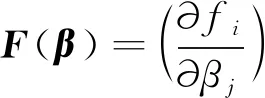
βk+1=
βk+(G(βk)TQ-1G(βk))-1G(βk)TQ-1(U-F(βk))。
(7)
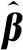
1.2 定位精度分析
(8)
式(8)中,
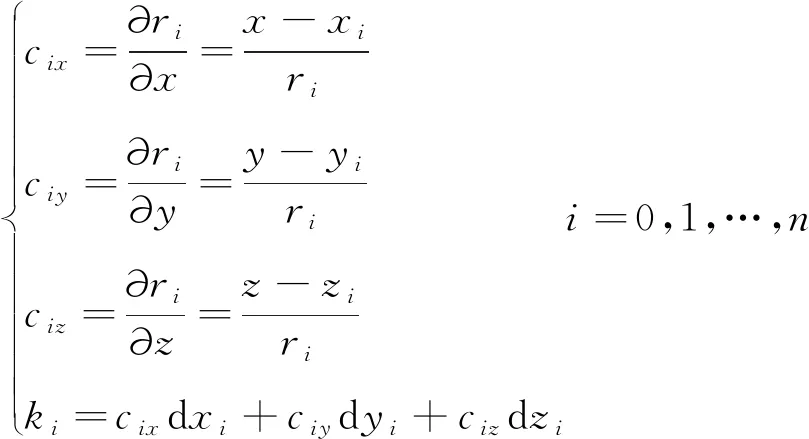
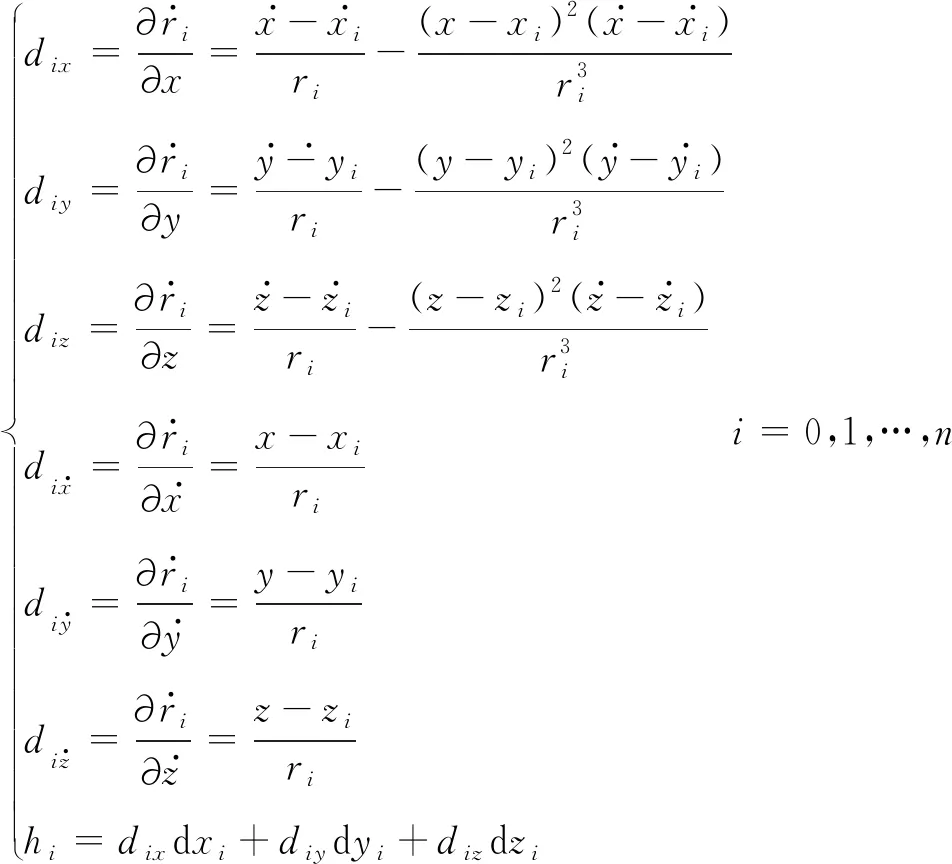
令
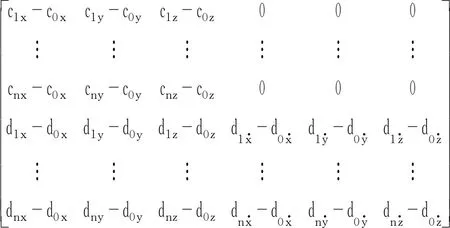
(9)
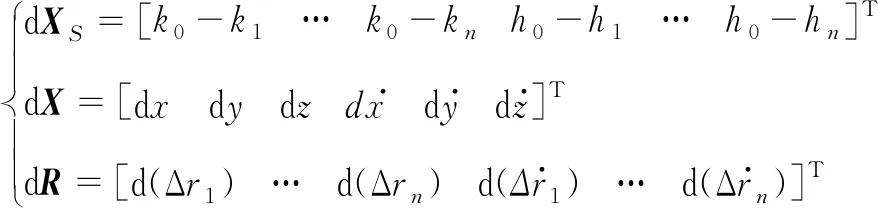
(10)
则误差方程式(10)的矩阵形式为
dR=CdX+dXS,
(11)
因此用伪逆法求解目标定位误差估计值
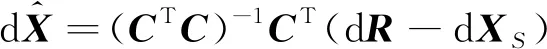
(12)
令
(CTC)-1CT=B=(bij)6×2n。
(13)
由Δri=ri-r0可知,各时间差测量中均包含了主站测量到达时间的误差,即各站时间差测量中包含共同的误差因素,故各Δri的观测误差是相关的。假设经修订后Δri测量误差为零均值,而在每次测量中站址误差保持不变,且站址误差各元素之间及各站误差之间互不相关,故定位误差协方差为:
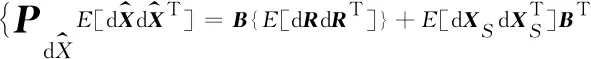
(14)
式(14)中,
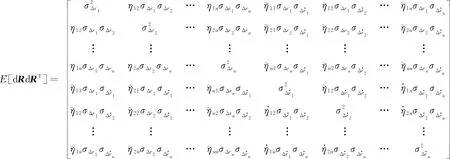
(15)
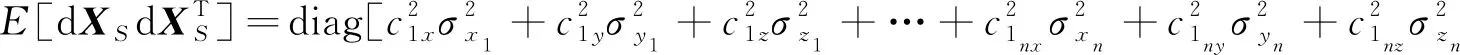
(16)
令
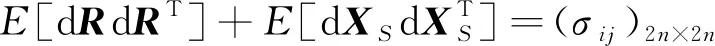
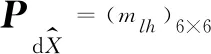
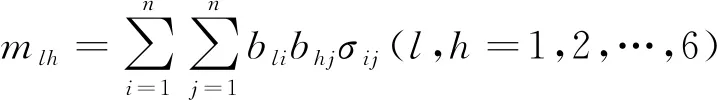
因此可得定位误差及速度误差在x,y,z方向上的方差:
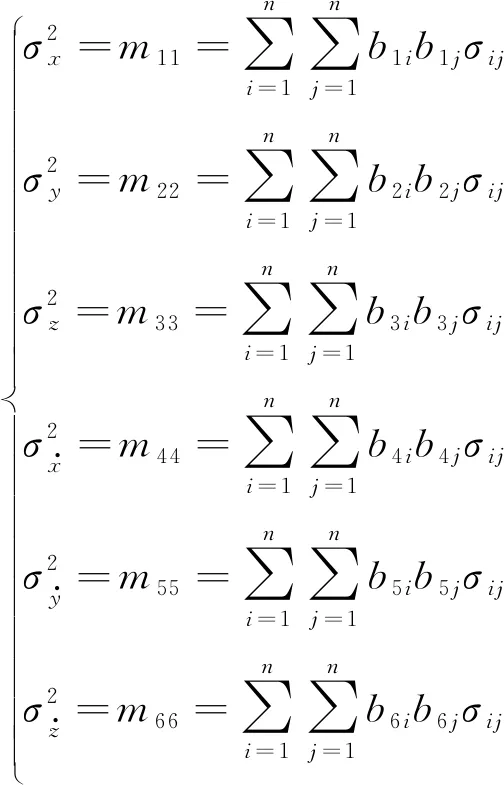
描述定位误差与几何的关系用“几何精度因子”,即GDOP[5],其表示为:
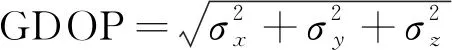
(17)
由式(17)可知,定位精度与站址误差及TDOA的测量误差的方差有关,且空间目标与各无源雷达站的几何位置关系对定位精度有影响[6]。
1.3 目标函数
无源雷达组网用于完成空间目标定位任务,对定位精度要求较高,因此将测量区域内位置平均精度作为最优目标函数,定义精度函数如下:
(18)
式(18)中,q为预警飞行区域内离散后的测量点数。
当空间目标飞行区域和测元误差等参数确定后,opt与各测站的位置相关,在布站设计中测站高程可取该离散后区域的众数值,若设各站的坐标为(xi,yi),则有:
opt=f(x1,y1,x2,y2,…,x4,y4)。
(19)
最优布站则要求确定(x1,y1,x2,y2,…,x4,y4)的值使opt为最小。
1.4 约束条件描述
测量系统布站的约束条件一般包括布站区域、设备工作仰角及山体遮挡。
1) 布站区域约束
布站区域约束是指可用于布站的地域,为简化计算,在地图上可采用线段逼近实际区域的边界,它是坐标x、y的函数,区域约束条件可具体表示为:
(20)
式(20)中,φ1、φ2为布站区域X坐标的最小、最大值,λ1、λ2为Y坐标的最小、最大值;ai、bi、ci为系数,由通过线段的两个端点坐标确定;这样,对一个地理坐标点(x,y),通过计算是否满足上式,就可判断其是否在区域D内。
2) 雷达工作仰角约束
无源雷达站对工作仰角有一定的要求,若仰角过低,则不能通视空间目标航迹或保证测元的精度。若设备的最低工作仰角为E0,为保证设备正常工作,则要求跟踪仰角E≥E0。
3) 山体遮挡
无源雷达站的覆盖半径不仅受到探测远界540 km的限制,还受山体遮挡的影响。空间目标的雷达信号以电磁波形式传播,电磁波信号沿直线传播到雷达站。因此在建立无源雷达站的覆盖模型时有必要考虑地形遮蔽对接收雷达信号的影响。基于雷达信号的传播特点,当有障碍物存在于电磁波的传输路径上时,空间目标机载雷达所发出的信号就无法被无源雷达站接收到,形成一个信号盲区[7-9]。如图2所示,沿无源雷达站接收天线与障碍物顶端做一条射线,该射线与水平面夹角为θ1,这时在山体后面会形成一个盲区,当空间目标与雷达站夹角小于θ1时,空间目标机载雷达所发出的信号无法被无源雷达站接收到。
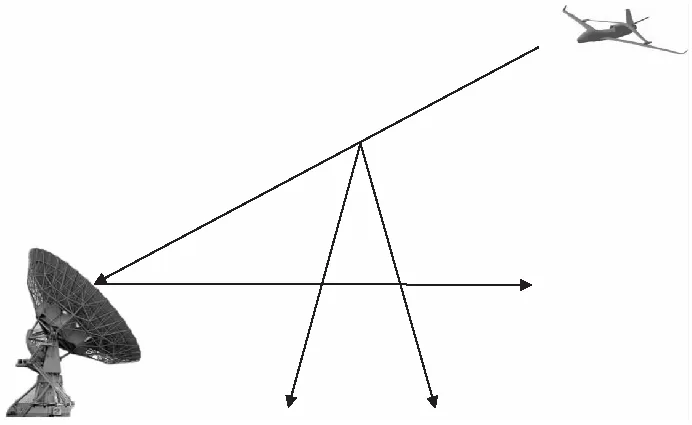
图2 仰角对覆盖盲区的影响Fig.2 The effect of elevation angel on coverage hole
空间目标与无源雷达站的水平夹角为
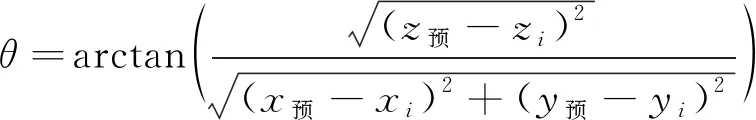
当θ>θ1时,雷达站可以接收到空间目标信号,否则空间目标在信号盲区内,由于山体遮挡,无法收到信号。
2 无源雷达组网布站方案及优化
2.1 地形数据分析
由于地形数据量大,采样周期不规则,由此基于OpenGL引擎,搭建OpenSceneGraph框架平台,采用点云的方式渲染了地形数据,获得可视化地形数据如下,见图3—图5,图中地形最低点配色为蓝色(RGB:0F0FFF),最高点为红色(RGB:FF0F0F)。

图3 地形数据俯视图Fig.3 Top view of topographic data

图4 地形数据图(高度Z×20)Fig.4 Topographic data map (height Z×20)

图5 地形数据正视图(高度Z×20)Fig.5 Topographic data front view (height Z×20)
由图3可知,图中地势范围大且平坦,山地较少;为获得更为直观的地势图,图4和图5将高度Z值乘以20。由图5可知区域内存在悬崖情况,即高度迅速变化区域。
2.2 区域离散化
将无源雷达站可部署区域视为一个矩形D1,空间目标飞行区域视为一个矩形D2,雷达布站点采用直角坐标表示,由布站位置可知雷达探测威力范围[10]。对布站区域进行离散化处理,将布站区域分成100×100的网格,横坐标方向间隔为dx,纵坐标方向间隔为dv,网格化后的布站区域如图6所示。
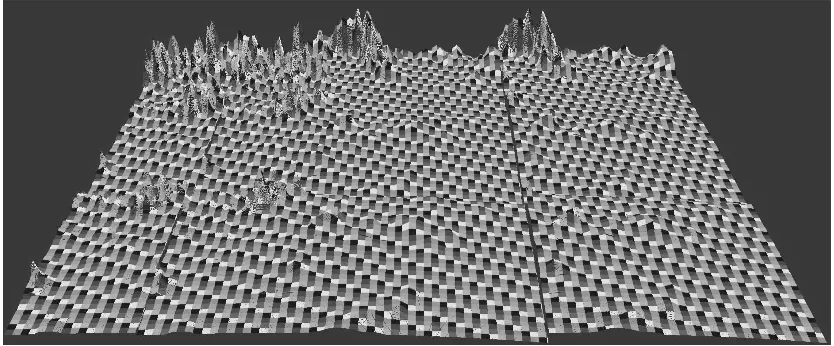
图6 布站区域离散化100×100网格图(高度Z×20)Fig.6 Discretization of station 100×100 layout grid map (height Z×20)
雷达布站位置矩阵记为G=(aij)M×N,其中,
aij=0,表示在第i行第j列的位置无部署阵地;
aij=1,表示在第i行第j列的位置有部署阵地。
第j套武器部署位置的坐标(xj,yj)可直接用其在矩阵中的位置表示,即xj∈[1,M],yj∈[1,N],i=1,2,…,n,则武器位置(xj,yj)∈Σ等价于
2.3 遗传算法的最优布站求解过程
需要对4个无源雷达站进行选址,在布站约束范围内进行遍历求解是不现实的,因此考虑使用智能算法搜索最优解。遗传算法是通过模拟自然进化过程搜索最优解的方法,针对数据量较大的组合优化问题有着较好的优化结果。基于遗传算法的雷达武器布站方案求解步骤为:
2.3.1 适应度函数
约束条件可采取罚函数进行处理,即当前布站方案不满足条件时,则罚函数赋予极大的野值,因此适应度函数可表示为:
F=opt+ΦD+ΦE+Φθ,
(21)
式(21)中,ΦD、ΦE、Φθ分别为布站区域、设备工作仰角、山体遮挡的罚函数,取值如下:
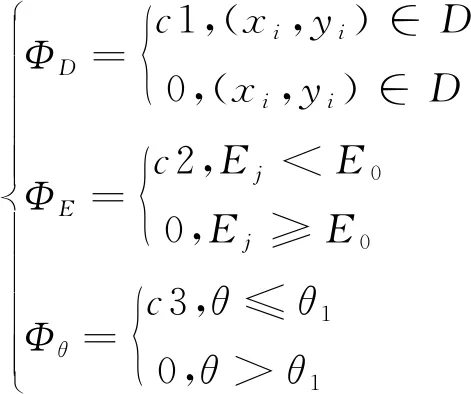
(22)
式(22)中,i表示一站点,j表示测量参数点。c1、c2、c3为远大于正常opt值的常数。
1) 初始化
设置进化代数计数器t=0,设置最大进化代数T=400,随机生成40个个体作为初始群体Ω0,此处每个个体代表一种布站方案,每种方案需要完成4个武器的位置部署。
2) 个体评价
计算群体Ωt中每个个体的适应度,利用Matlab计算过程如下:
a) 设置仿真初始参数——无源雷达初始部署坐标和空间目标位置信息等参数;
b) 计算出每种布站方案对飞行区域内的离散点的定位误差GDOP。
3) 设置交叉率和变异率
本题中设置交叉率为0.8,变异率为0.2。
4) 终止条件判断
当终止条件满足以下两者其一时,算法终止:a) 若此代和上一代的适应度之差小于0.05时,迭代结束;b) 若结果不随每代收敛,则满足t=T时,算法终止。
2.3.2 计算结果
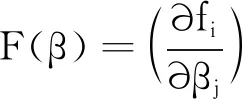
通过多轮遗传算法求解,可得7个局部最优解, 7个布站方案如图7所示。

图7 7个局部最优解的布站方案示意图Fig.7 Schematic diagram of the station layout scheme of 7 local optimal solution
通过计算可获得多组局部最优的布站结果,接下来根据布站方案进行遮挡情况的检验矫正。
3 仿真验证与方案筛选
根据上述7个备选布站方案可知,雷达布站方案GDOP平均为1 347.476 m,GDOP差别在1.5%以内时,不同方案的定位精度偏差约20 m,该定位精度偏差在引导信息和空间目标尺寸下可近似忽略。
分析以上7种布站方案,可按如下步骤进行布站方案的二次优化,以此达到方案筛选目的。
步骤1 首先按照GDOP值将备选布站方案按从小到大排序;
步骤2 根据备选方案排序顺序,分别计算每个备选方案在目标飞行区域的遮挡情况。如果有遮挡,则当前布站方案不满足空间目标的定位解算,即存在探测盲区,因此该方案被舍弃;如果无遮挡,则选其为最终方案;
步骤3 如果所有备选方案都存在遮挡问题,则重新备选方案排序,在布站周围画1 200 m×1 200 m的方框,在周围以dx,dy为步长,搜寻定位精度更高、遮挡情况更少的布站方案,最终确定布站方案。
7种方案的GDOP均值排序见表1。
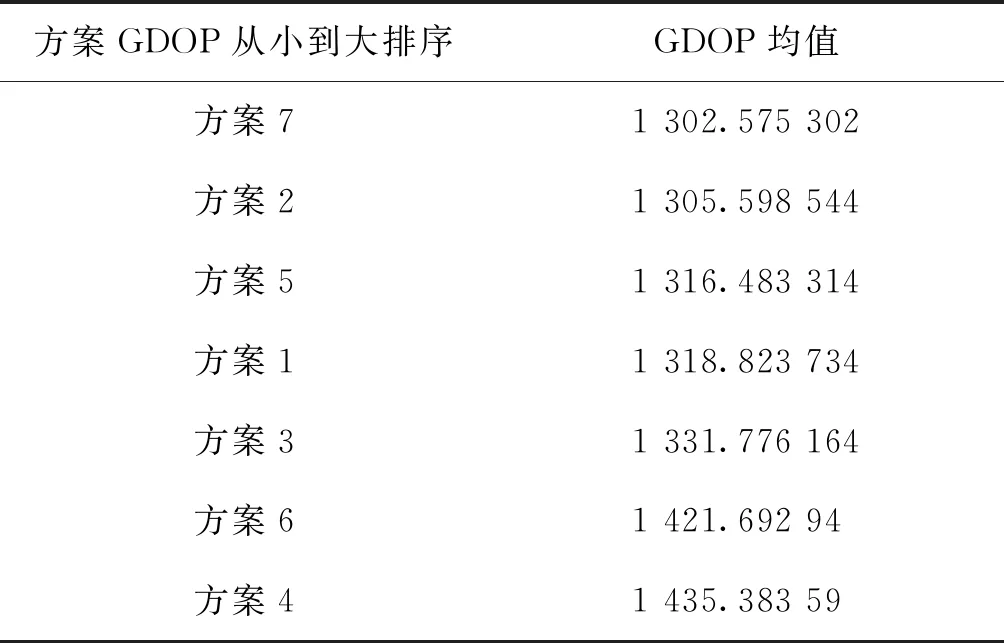
表1 7种方案的GDOP均值表Tab.1 GDOP mean table of 7schemes
根据遮挡情况和定位精度综合筛选,方案5在飞机区域内无遮挡,且方案5与方案7的GDOP均值相差1.1%,满足条件,因此最终确定方案5最优布站。
4 结论
本文将无源雷达站定位空间目标的复杂问题分解,通过合理的假设,简化模型,建立定位精度分析和雷达布站优化仿真等模型,较好地解决了问题。在布站区域仿真优化时,基于OpenGL引擎,搭建OpenSceneGraph框架平台,采用点云的方式渲染了地形数据和布站数据,运用可视化技术,使布站方案显示更直观。通过遗传算法逐步迭代,不断优化,得出相对较好的雷达布站方案,为无源雷达定位空间目标的雷达位置选择提供指导。
