Shock wave and bubble characteristics of underwater array explosion of charges

Hong-Wei Hu ,Pu Song ,Shuang-feng Guo ,Hai-yun Feng ,Dao-kui Li

a College of Aerospace Science and Engineering,National University of Defense Technology,Changsha,410073,Hunan,China

b Xi'an Modern Chemistry Research Institute,Xi'an,710065,Shaanxi,China

c Hunan Key Laboratory of Intelligent Planning and Simulation for Aerospace Missions,Changsha,410073,Hunan,China

Keywords:Explosion mechanics Underwater explosion Array explosion Shock wave Bubble

ABSTRACT In this study,we focused on the effect of the underwater explosion parameters of multi-point array explosion.The shock wave and bubble parameters of aggregate charge,two charges,and four charges were measured through an underwater explosion test,and their influence on the explosion power field of charge quantity and array distance was analyzed.Results show that the multi-shock wave collision of array explosion can be approximated to a linear superposition,and the interaction of delayed shock wave can be deemed as the increase of the shock wave baseline.Shock wave focusing and delayed superposition increase the shock wave peak pressure.Compared with the aggregate charge,the greater the number of array explosion points is,the higher the impulse and the gain of the bubble peak pressure are.At the same array distance,the smaller the charge quantity is,the higher the bubble impulse will be.At the same charge quantity,the smaller the array distance is,the higher the bubble impulse will be.The bubble period decreases gradually with the increase of the charge quantity,but the test orientation has little effect on the bubble period.

1.Introduction

Improving the damage effect of ammunition has always been a major issue concerned by weapon designers.Array explosion is a special optimization control technology of explosion energy,the utilization rate of explosion energy is improved significantly.

First,we briefly introduce array explosion concepts.By arranging explosion units and precisely controlling the initiation time of each explosion unit according to the design layout and sequence,the optimized distribution of damage elements is realized in time and space dimensions [1].Next,we present the following advantages of array explosion technology: the optimized distribution of explosion energy expands the effective damage area and improves the effective utilization rate of explosion energy;multiple damage elements produce simultaneous or sequential cumulative damage effects,which improve the transforming efficiency of explosion energy into damage effect;and the vector superposition of explosion parameters enhances the strength of the damage element in the local area or a specific direction[1].It has important application prospect in blast warhead,underwater warhead and penetration warhead,etc.

In this section,a brief summary of relevant research is provided.The pioneer work can be traced to the research of Philips,who is experts of the US Nuclear Defense Agency [2].They studied the simultaneous explosion of seven bombs with an equivalent of 500,000 tons at an underground depth of 500 m;the area with a stress greater than 51 MPa exceeds 1 km.The high stress area is significantly larger than the single bomb explosion area,and the pressure peak is 3-4 times higher than that of the single bomb explosion in the specific area.Through many simulation calculation and chemical explosion simulation tests,Sandia Laboratory of the United States [3] analyzed the explosion accumulation effect of seven 500,000 tons nuclear penetrating bombs in hexagonal arrangement(i.e.,six bombs in each corner of the hexagon and one in the geometric center;the detonation depth is 12 m;and the spacing distance is 400 m).The ground shock effect is equivalent to a single nuclear bomb of 20 million tons in the focusing sites,and the explosion efficiency improved by six times.In addition,the depth of the 100 MPa pressure of the seven bombs is 80% higher than that of the 3.5 million ton single bomb.Chen[4]reported that under the same condition,the damage area of a two-point explosion is higher than that of a single point explosion in air.Li et al.[5]studies show that the focusing results in a very large nonlinear increase of the normal strain in the focusing area with high stresses over a large area around the explosive location,which can lead to serious material and structure damage.Hu et al.[6] studied the shock wave interaction of two and three charges in a ground synchronous burst.The shock wave overpressure and impulse increased significantly.Under the same total mass of charge,the greater the number of charges is,the higher the overpressure and impulse are,and the increase of the overpressure and impulse of the shock wave vary for charges with different layouts.The collision of shock waves with a rigid wall can be used to approximately calculate the interaction between two shock waves of equal intensity.

However,the research on array explosion mainly focuses on underground and air explosions,and limited research has been conducted on underwater array explosion.The explosion two charges at the bottom in a shallow layer was simulated numerically[7].The explosion processes of single and two charges explosions at the bottom of a shallow layer water were compared.Affected by the free surface and bottom,the maximum value of shock wave pressure and its impulse decreased.During the reaction of two waves,the blasting power must be increased.The interaction law of the multi bubbles of two or more charges underwater explosion was simulated in the literature[8-10].The focusing effect of the shock waves and the nonlinear merge of multi-bubbles contribute to the complexity of the power field of a multi-bomb array explosion,but the relevant laws and mechanisms remain unclear.

Through an underwater explosion test,the influence of array distance and charge quantity on the shock wave and bubble parameters of underwater explosion is analyzed.The effect of multi charges array explosion on the underwater explosion power field is obtained,providing theoretical support for the regulation of underwater explosion power and the design of a new damage mode.

2.Experimental

2.1.Experimental samples

The PBX explosive is composed of a RDX/Al/AP/binder.The aluminum powder is spherical,with an average particle size of 5 μm and a charge density of 1.81 g/cm.The charges masses are 0.25 kg,0.50 kg,and 1.0 kg.The aggregate charge is 1.0 kg,two charges are formed by a pair of 0.50 kg charges and four charges consists of four 0.25 kg charges.The booster explosive of the 0.25 kg and 0.50 kg charges is JH-14 with a mass of 10 g,and the booster explosive of the 1.0 kg charge is JH-14 explosive with a mass of 35 g.The mass ratio of the booster and the main charge is less than 4%.The initiation device is the No.8 copper detonator,which was installed at the center of the upper end face of the charge.Multiple detonators in series were used in the experiment,and the absolute deviation of ignition time of No.8 copper detonators were less than 1μs by experiment,which can meet the requirements of initiation synchronization [6].

The detonation heats of the PBX and JH-14 explosives are 7032 kJ/kg and 5940 kJ/kg,respectively,and the equivalent of JH-14 to PBX is 0.845.When PBX was used as the standard explosive,the total masses of the three types of charges were 1029.7 g(aggregate charge),1017 g (two charges),and 1033 g (four charges).The relative error of the charge mass of the test sample was less than 1%,indicating that the influence of the charge quality difference on the explosion parameters was very small.

2.2.Experimental layout

The test pool is oval,the long axis is approximately 130 m,the short axis is approximately 80 m,and the water depth is 24 m.A 1.0 kg aggregate charge is suspended in water by nylon rope.For double and four charges,the array distance(L)of the charge on the cross-wood support is first determined.Then,the charges is fixed on the wood support with a cotton rope,and the heavy hammer is hung at the bottom of the charges.Next,the lifting rope and the direction control line are connected with a wood support and hung in the water.Finally,the direction control line is fixed on the steel cable.Two measuring points with an included angle of 45are set up,and one sensor is placed at every measuring point.The distance between the measuring point and the charge or the symmetrical center of the two and four charges is 3 m.The depth of both sensors and charges is 8 m,previous experiments show that the free surface and bottom have little effect on the parameters of underwater explosion.Taking the two charges as an example,the test layout is shown in Fig.1.

The charge layout in different test conditions is shown in Fig.2.L is the array distance,the distance between them is two charges,and the distance between the diagonal charges is four charges.

The calculation formula Eq.(1)for the bubble radius is as follows[11]:

where ris the bubble radius,m;W is the charge mass (TNT equivalent),kg;and H is the depth of charge in water,m.

The bubble radii of the charges with different masses is calculated as follows,as shown in Table 1.

To ensure the interaction of multi bubbles,the array distance between charges is set within the bubble radius,as shown in Table 2.

Table 1.Bubble radii of underwater explosion for different mass charges.

Table 2.Array distances of charges.

2.3.Experimental instrument

The 138A model of underwater tourmaline blast sensor from the United States PCB company.Its main property are as follows:measurement range from 0 to 34.5 MPa,rise time less than 1.5 μs,resonant frequency more than 10 MHz.

DEWE-5000 model signal adapter were employed in the underwater explosion test system with 10 MHz sampling rate and 16-bit resolution.

The sampling frequencies of the shock wave and bubble pulse signals are 10 MHz and 100 kHz,respectively.

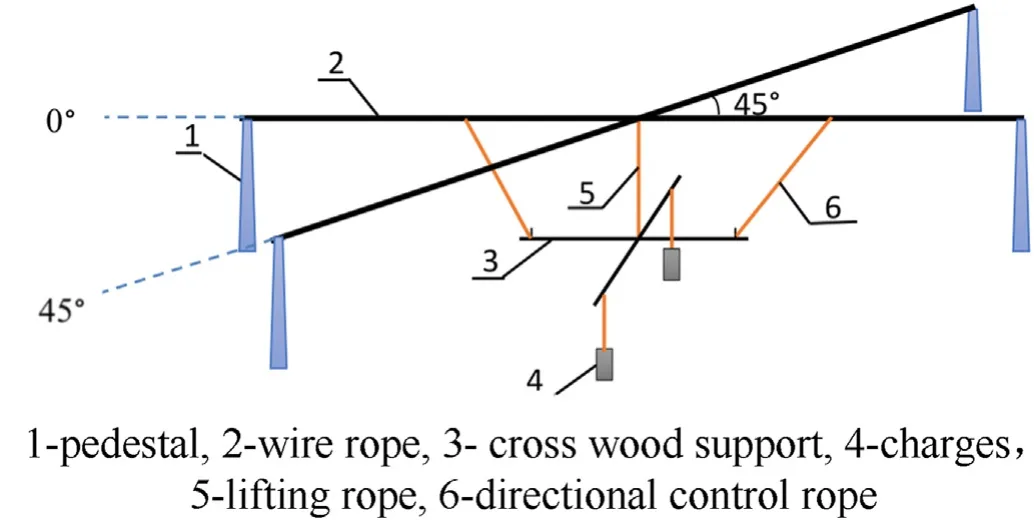
Fig.1.Experiment layout (two charges).

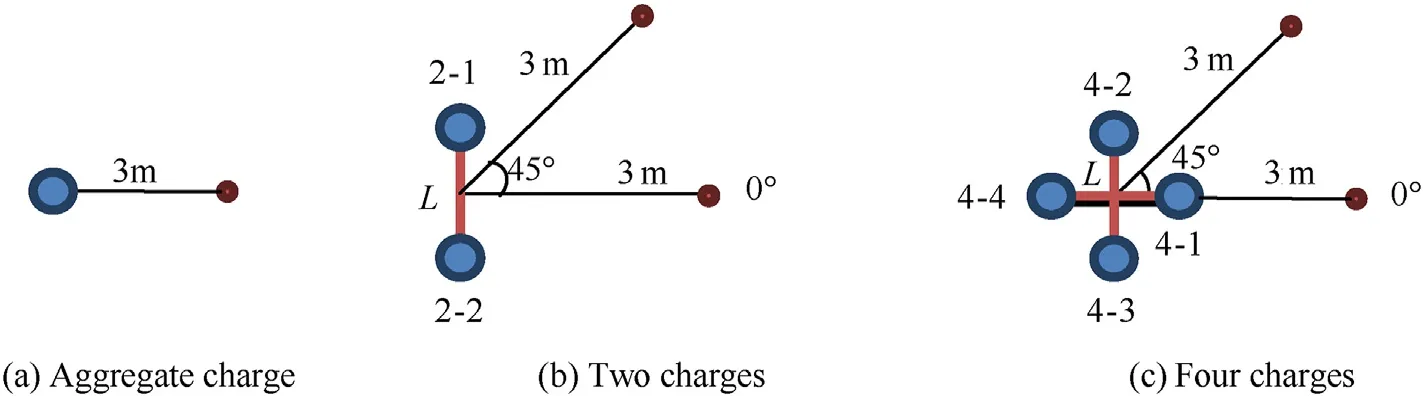
Fig.2.Charges layout.

3.Data processing method of multi charges array explosion

The peak pressure of the shock wave can be read from the pressure time curve.However,the coupling of multi shock waves leads to the attenuation process of pressure instead of exponential attenuation;the integral time constant of impulse cannot be taken as 5.0 θ or 6.7 θ.Through the analysis of experimental data,the integral time of impulse is set to 1 ms,which can cover the pressure time history of the shock wave for all test conditions.The bubble impulse is calculated by the method in the literature [12].

The ratios of different characteristic parameters are as follows:

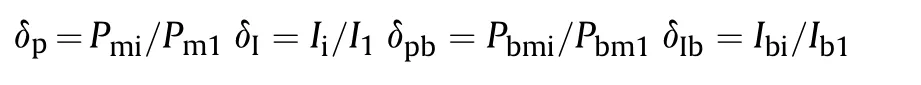
where δ are the ratios of parameters;P,I are peak pressure and impulse,respectively;subscripts b,1 and i represents bubble,the aggregate charge and the number of array charges,respectively.

4.Results and analysis

4.1.Experimental results

4.1.1.Underwater explosion of aggregate charge

The shock wave and bubble curve of underwater explosion for the 1.0 kg aggregate charge are shown in Fig.3.

As shown in Fig.3,the pressure time curve of underwater explosion is smooth,and the bubble pulse has only one pressure peak(see Fig.3d).

The shock wave and bubble parameters of underwater explosion for the 1.0 kg aggregate charge are shown in Table 3.

Table 3.Shock wave and bubble parameter of underwater explosion for 1.0 kg aggregate charge.

Although the peak pressure of the bubble pulse is 23%(approximately 1/5) of the initial shock wave,the impulse of the bubble pulse is 3.38 times that of the initial shock wave.

4.1.2.Underwater array explosion of two charges

When the array distance is 1.0 m,the shock wave and bubble pulse curve of the underwater explosion for two 0.50 kg charges are shown in Fig.4.

In the 0test direction,the shock waves formed couple by charges 2-1 and 2-2,and the difference in arrival time between the two shock waves is 14 μs.The peak pressure of the first shock wave is 10.23 MPa,and the peak pressure of the second shock wave from arrival reached the highest point of 10.37 MPa.If the two shock waves are entirely superimposed,then the peak pressure of shock wave is 20.6 MPa.In addition,the difference between the peak pressures of the initial and second shock waves is 1.68 MPa,the maximum peak pressure in Fig.4a is 18.92 MPa,and the sum of the two is 20.6 MPa.Thus,the collision of two shock waves with the same strength is equivalent to the reflection of shock waves on the rigid surface [6,13],which forms a linear superposition.In the 45test direction (see Fig.4b),the arrive time difference between the two wave peaks is 44.3 μs due to the different distances between the test point and the two charges(see Fig.2).The peak pressure of the first shock wave is 11.03 MPa,and the peak pressure of second shock wave is 10.19 MPa.Although the coupling of the two shock waves was delayed,the peak pressure of the second shock wave still increased.The first shock wave has not decayed completely when the second shock wave arrives,which is equivalent to raising the baseline of the second shock wave.Thus,if the latter shock wave produces delay coupling with the front shock wave,the peak pressure of the latter shock wave increases.

Fig.4c-f shows that the rising front and the peak of the bubble have burr shaped fluctuations,because of the disturbance of the unsteady interface during the fusion process of the two bubbles.

4.1.3.Underwater array explosion of four charges

(1) Array distance is 0.5 m

When the array distance is 0.5 m,the shock wave and bubble pulse waveform of the underwater explosion for four 0.25 kg charges are shown in Fig.5.

The wave sharp given in Fig.5a shows that three shock wave pressure peaks coupled in the 0-degree test direction.The pressure peak of the first shock wave was generated by charge 4-1,which is nearest to the sensor.The peak pressure of the second shock wave was generated by symmetrical charges 4-2 and 4-3,and the arrival time difference was 32 μs due to the deviation of the charge placement positions.However,the peak pressure of the second shock was still higher than the first and third shock wave.The peak pressure of the third shock wave was generated by the charge 4-4,which is farthest from the sensor,and the peak pressure increased because of the superimposition with the second shock wave.The peak pressure of the three shock waves were 8.98 MPa,14.81 MP,and 10.26 MPa,respectively.Fig.5 b indicates that in the 45-degree test direction,the peaks pressures of three shock wave increased gradually,and the peak pressures were 7.91 MPa,11.54 MPa,and 12.63 MPa,respectively.The shock waves generated by the charges 4-1 and 4-2 explosion did not complete the superposition,and the difference between the two shock waves was 78 μs The third shock wave was the coupling of the underwater shock waves by the charge 4-3 and 4-4 explosion,and its peak pressure was higher than the first and second shock waves.Not only were the shock waves completely superposed by the charge 4-3 and 4-4 explosion,but the second shock wave had not completed the amplitude when the second shock wave arrived.Therefore,it arrived before attenuation,and superposition occurred.Therefore,the shock wave superposition of charges array explosion can produce multiple cumulative high-pressure shock damages to the target in a short time (500-700 μs).

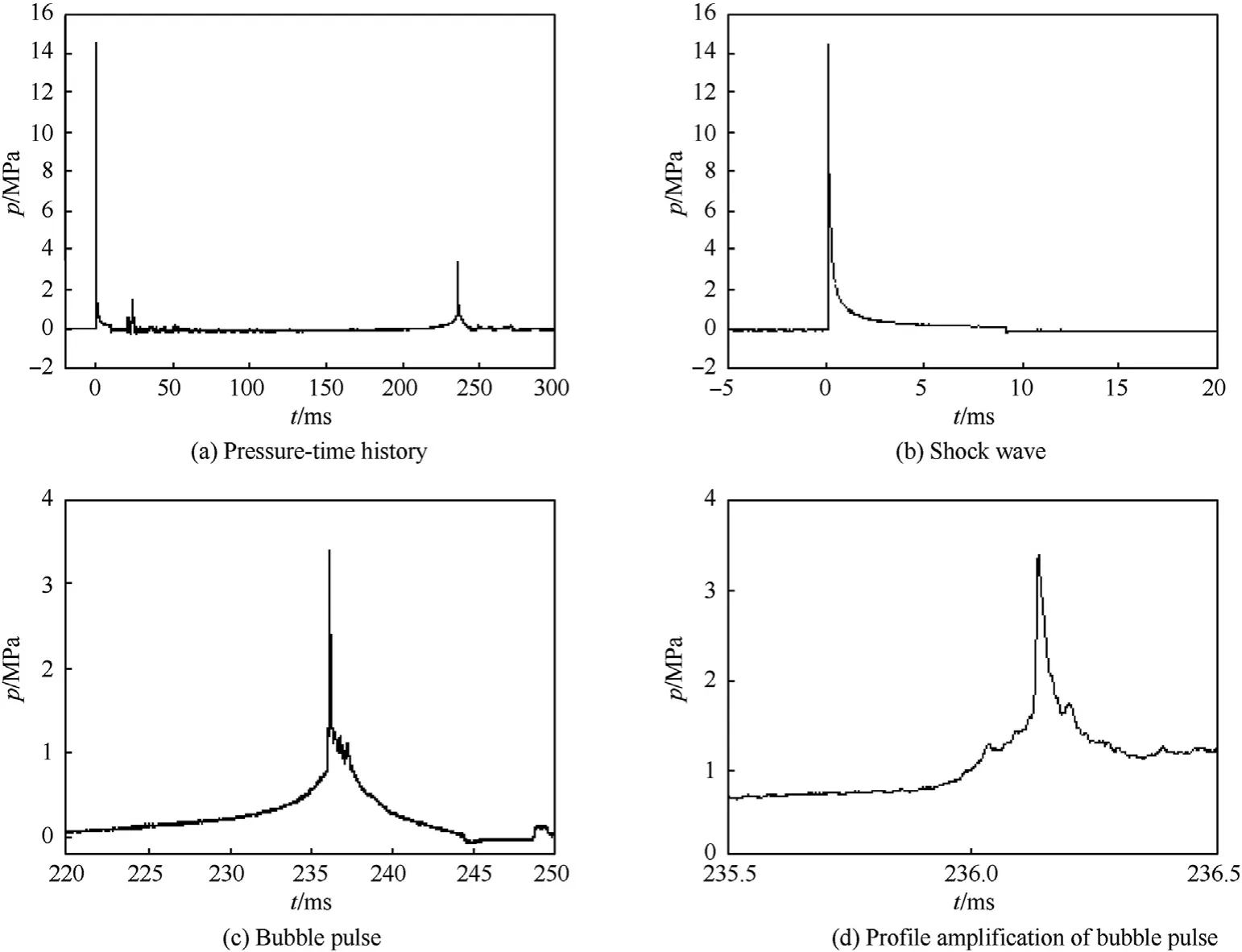
Fig.3.The shock wave and bubble profile of underwater explosion for 1.0 kg aggregate charge.

Fig.5c-d indicate that a low-pressure wave appeared at 219.1 ms,and a large-pressure wave appeared at 226.8 ms.The first pressure wave may have been caused by the collision of four bubbles in the contraction stage,while the second pressure wave was generated by the bubble expansion after the bubble fusion,so 226.8 ms is the bubble period.Fig.5e-f shows that the bubble pulse curve is very irregular,and the jitter is very severe.These phenomena can be caused by the strong disturbance of the interface during the fusion process of four bubbles.

(2) Array distance 1.0 m

When the array distance is 1.0 m,the shock wave and bubble pulse waveform of the underwater explosion for four 0.25 kg charges are shown in Fig.6.

In the 0test direction,the wave sharp given in Fig.6a shows that the peak pressure of the first shock wave was generated by charge 4-1,which is nearest the sensor.The pressure wave of two symmetrical charges (4-2 and 4-3) superimposed to form the second shock wave.The third shock wave was produced by charge 4-4,which is farthest from the sensor.However,the second and third shock waves were not amplified due to the deviation of the charge placement positions,and the arrival time difference between the two waves was 21 μs Thus,the peak pressures of the four shock waves were not superposed,and the peak pressures were 9.30 MPa,9.30 MPa,9.61 MPa,and 5.50 MPa,respectively.However,when the latter shock wave arrived,the front shock wave attenuated to a lower pressure,so the gain of the shock wave pressure was not high.In addition,two smaller peak pressures of shock wave were observed between the third and fourth shock waves,and the peak pressures were 3.32 and 3.16 MPa,respectively,which may be the Mach wave by the collision of several blast waves.In the 45test direction,though the shock wave pressures of charges 4-1 and 4-2 were not superposed completely,and the arrival time difference of the shock wave was 20 μs(see Fig.6b),the peak pressure of the first shock wave was equivalent to 1.0 kg aggregate charge.The arrival time difference of the shock wave of charges 4-3 and 4-4 was 90 μs.The peak pressures of the shock wave were 5 94 MPa and 4.11 MPa.

Fig.6c to d indicate that a low-pressure wave also appeared at 217.2 ms,and another large pressure wave appeared at 225.4 ms.The reason is the same as the analysis for the array distance 0.5 m.It is considered that the first pressure wave may be caused by the collision of four bubbles contraction stage,and the second pressure wave is caused by the expansion of bubbles after fusion,so 225.4 ms is the bubble period.Fig.6e to f shows that the strong disturbance of the interface during the fusion process of the four bubbles resulted in an irregular bubble pulse waveform.However,when the array distance was less than 0.5 m,the bubble pulse jittered severely.Interestingly,the number and superposition trend of the bubble pulse pressure peaks are very similar to those of the shock wave,probably because when the array distance is great,the bubbles generated by the four charges explosion are approximately.However,due to the weak adsorption force,an interface remained between the four small bubbles.The separation tendency in the process of expansion resulted in multiple oscillations.

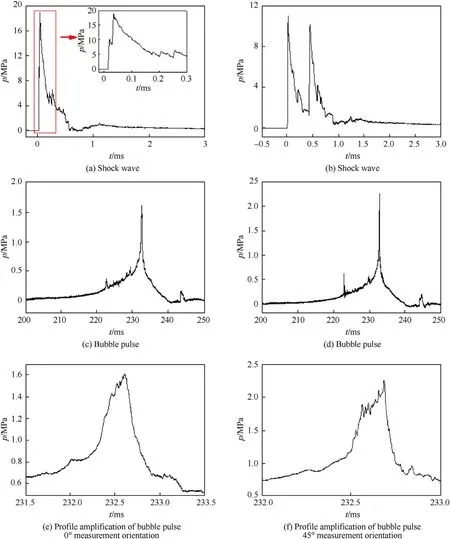
Fig.4.The underwater explosion shock wave and bubble profile of two 0.50 kg charges at the array distance of 1.0 m.

4.2.Effect of underwater array explosion on shock wave and bubble parameters

4.2.1.Effect of array explosion on shock wave parameters

The comparison of the shock wave parameters of underwater array explosion and aggregate charge is shown in Table 4.

The peak pressure gain of the shock wave for three kinds of array explosions is shown in Fig.7.

In the 0test direction,the peak pressure of the shock wave by the coupling of two 0.50 kg charges was the highest,exhibiting an increase of 22% compared with that of the 1.0 kg aggregate charge.The peak pressure of the shock wave decreased by nearly 30% in the 45test direction,but the two shock waves can produce a cumulative damage effect in a short time (hundreds of microseconds).For the four charges,the array distance was 0.5 m,and the shock wave pressure on the central axis of the symmetrical charge could be superimposed.In addition,because the charge distance was close,the pressure of the first shock wave was not attenuated to the lowest point,the later shock wave has reached,and cumulative multiple shock wave pressures were realized (asymmetric direction).The peak pressure of the shock wave was 81%-95% of the 1.0 kg aggregate charge,and it has four cumulative effect of shock wave.The array distance is 1.0 m,and the coupled peak pressure of the shock wave of the charges 4-1 and 4-2 explosion was 96% of the 1.0 kg aggregate charge.However,the peak pressure decreased by 40% in the 0test direction.The peak pressure of the latter shock wave arrived after the first shock wave decayed to a lower amplitude,so the cumulative superposition cannot be realized.

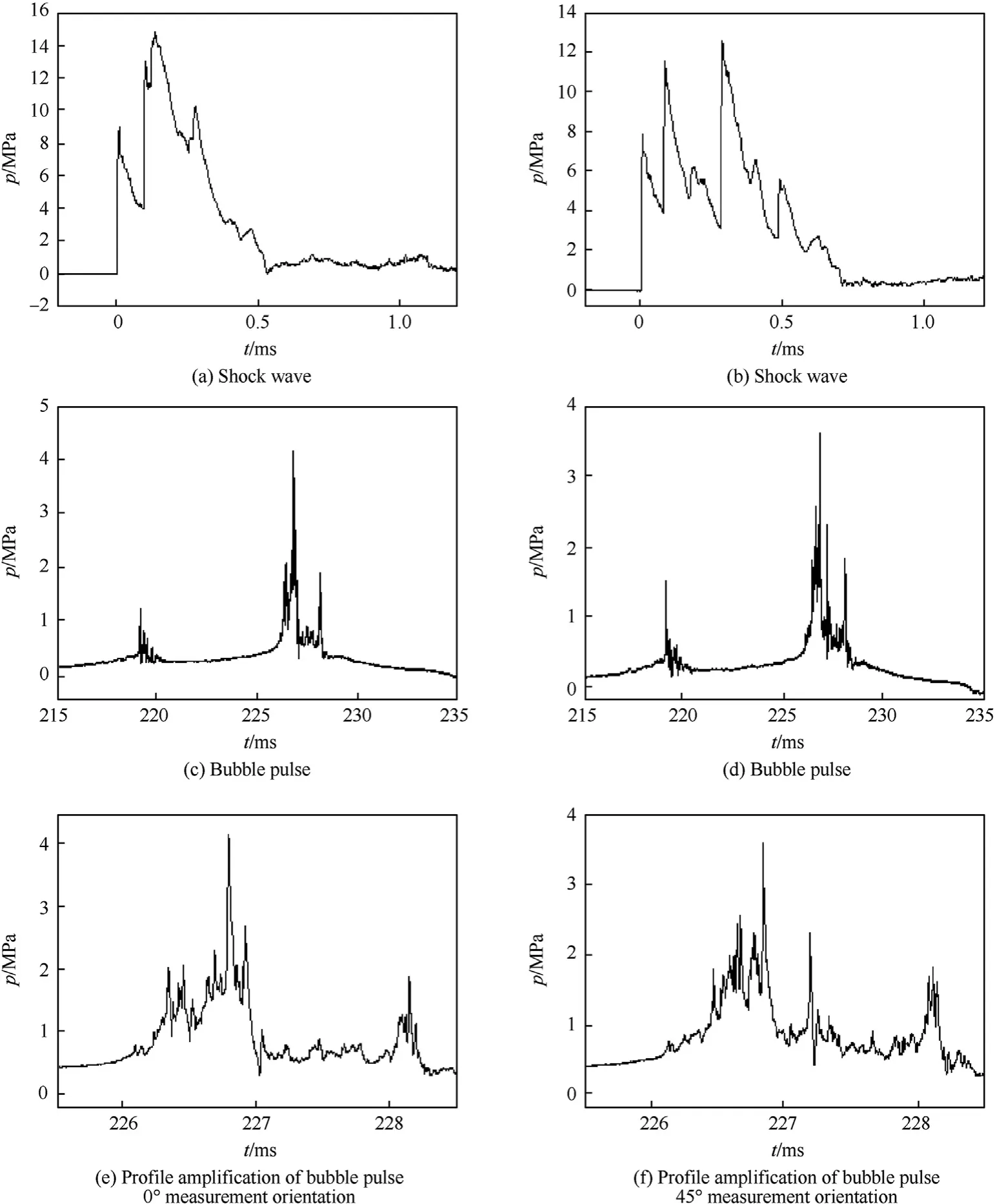
Fig.5.Underwater explosion shock wave and bubble profile of four 0.25 kg charges at the array distance of 0.5 m.

For the two charges,the peak pressure in the focusing direction of the shock wave increased significantly.For the four charges,under the same number of charges,the gain of the maximum peak pressure of the shock wave gradually decreased in the 0test direction (single focusing effect) with the increase of the array distance.The maximum gain of the peak pressure of the shock wave gradually increased in the 45test direction (double focusing effect).The gain of the shock wave peak pressure of the two charges was mainly in the focusing direction.When the charge array distance is close,the shock wave can also achieve delay time superposition.

The gain of impulse for the three array explosions is shown in Fig.8.

For the two charges array explosion,the impulse decreased by 19% and 24% compared with that of the 1.0 kg aggregate charge in both test directions.For the four charges array explosion,the array distance was 0.5 and 1.0 m,the impulse of is close to or higher than the 1.0 kg aggregate charge in both test directions.When the array distance is 0.5 m,the impulse increases by 19% in the 45test direction.The greater the number of the explosion points of the array is,the higher the impulse is,and the impulse with a small array distance is larger than that with a large array distance.

In addition,the peak pressure and impulse of multiple shock waves were still consistent with explosion similarity law for two charges and four charges array explosion [14].So when the array layout,array distance and initiation time sequence are determined,the explosion power field will be fixed.

4.2.2.Effect of array explosion on bubble parameters

The bubble parameters of underwater explosion between array charges and the aggregate charge are shown in Table 5.

Table 4.Shock wave parameter of underwater explosion between array charges and aggregate charge.

The gain of the bubble peak pressure of array explosions is shown in Fig.9.

Compared with the 1.0 kg aggregate charge,the peak pressure of the bubble pulse decreased by 35%-54% for the two charges array explosion in both test directions.For the four charges array explosion,except for the array distance of 1.0 m,the peak pressure of the bubble decreased by 20% in the 0test direction.The peak pressure of the bubbles was near or higher than the aggregate charge in other test conditions.The peak pressure of the four charges was near or higher than the aggregate charge.For the array is 0.5 m,the peak pressure of bubble is increased nearly 20% in the 0test direction.The more explosion points of the array,the higher the pressure peak of bubbles,and the higher the gain for small the array distance.

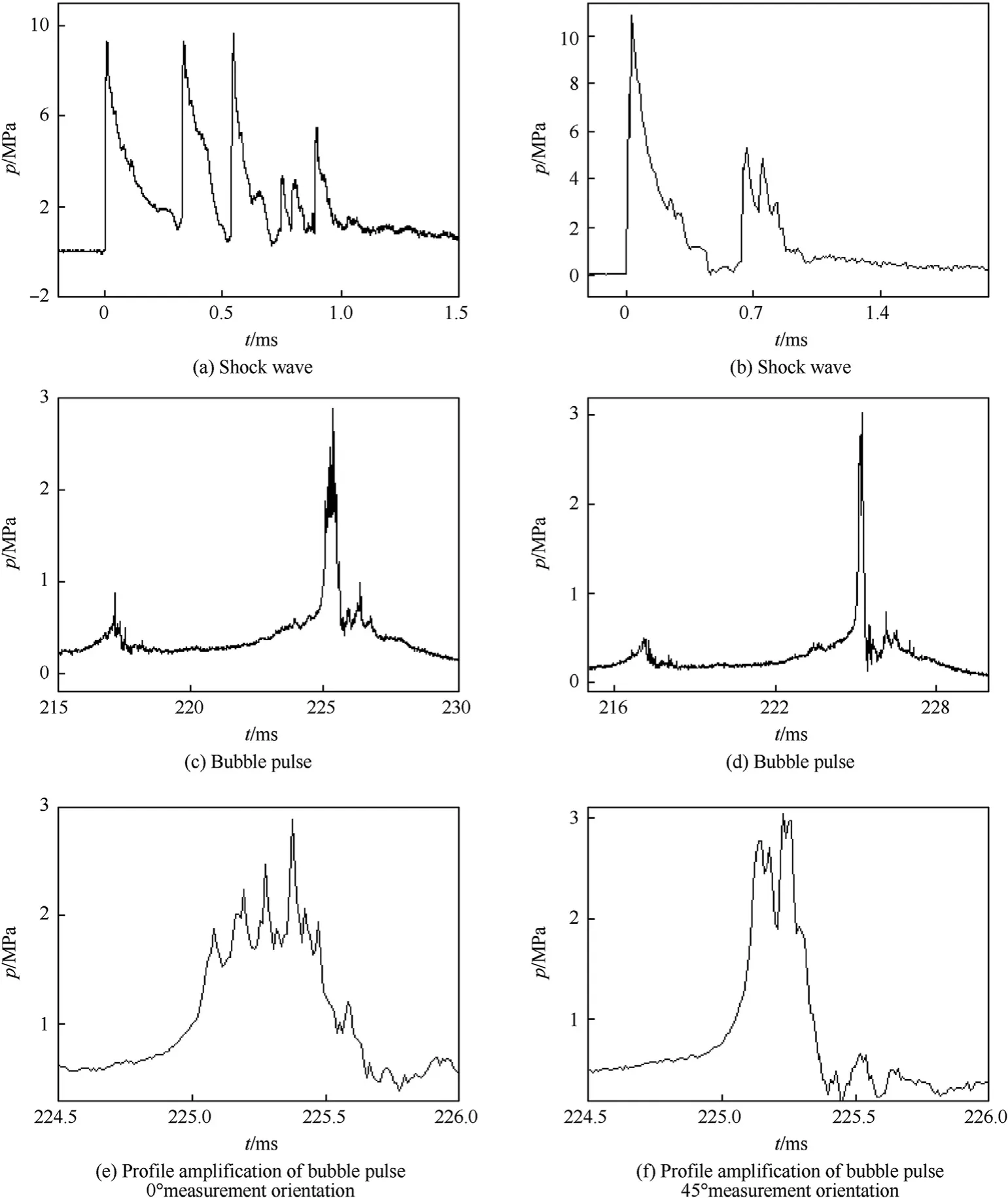
Fig.6.Underwater explosion shock wave and bubble profile of four 0.25 kg charges at the array distance of 1.0 m.

The gain of the bubble impulse for three kinds of array explosions is show in Fig.10.

The impulse of the bubble decreased significantly in all test conditions.The bubble impulse of two charges was higher than that of the four charges for the array distance of 1.0 m.For the four charges,the impulse of the bubble at the array distance of 0.5 m was higher than that at the array distance of 1.0 m.These results show that at the same array distance,the smaller the charge number is,the higher the bubble impulse will be.At the same charge quantity,the smaller the array distance is,the higher the bubble impulse will be.

The bubble period of the underwater explosion of the aggregate charge and array charges is shown in Table 6.

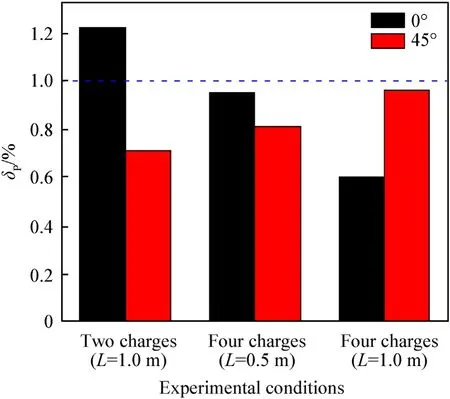
Fig.7.Gain of shock wave peak pressure for three kinds of array explosions.

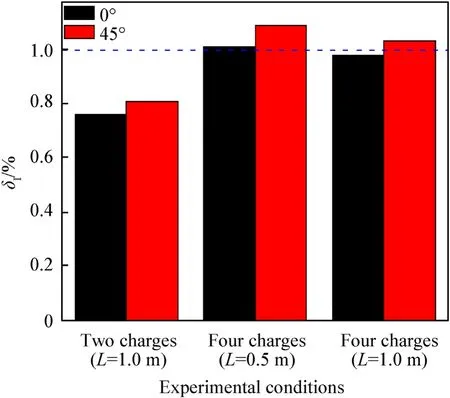
Fig.8.Gain of impulse for three kinds of array explosions.

The bubble period of the underwater explosion of the aggregate charge and array charges is shown in Fig.11.

Table 6 and Fig.11 indicate that the bubble period gradually decreased with the increase of the number of charges,but the value of decrease was less than 5%.The test direction had little effect on the bubble period.

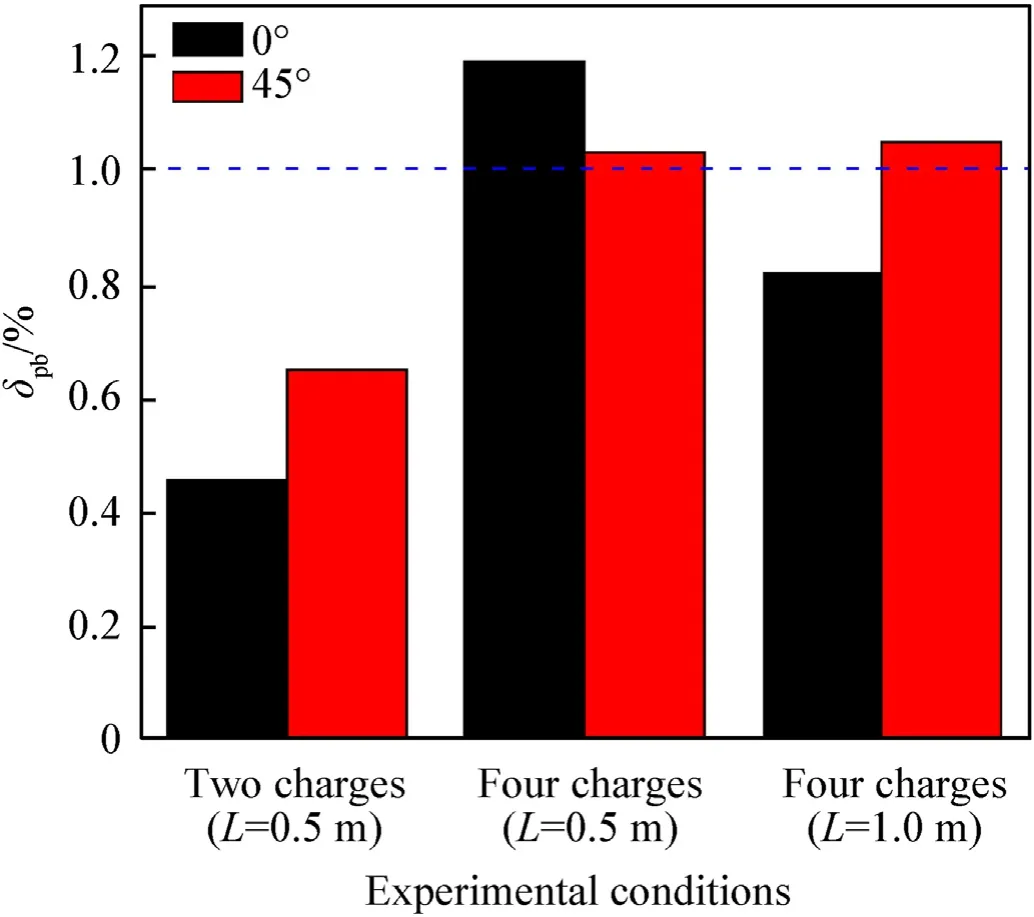
Fig.9.Gain of bubble peak pressure for three kinds of array explosions.

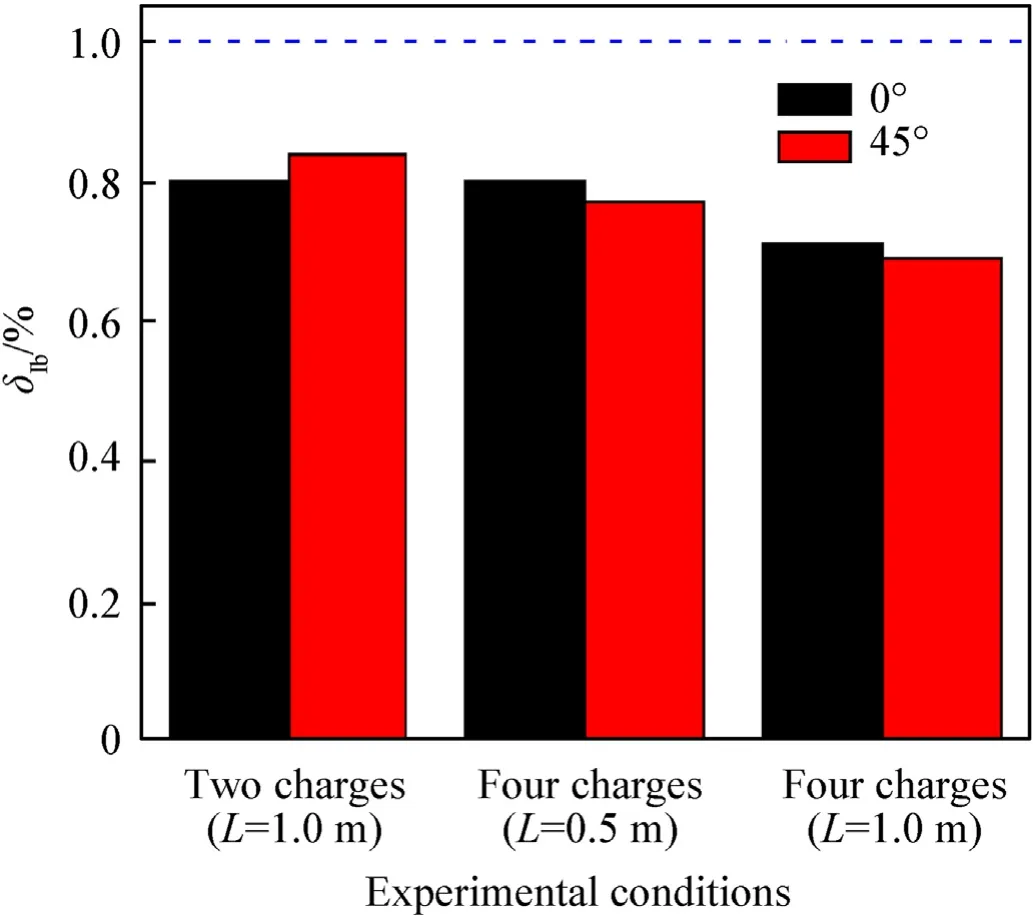
Fig.10.Gain of bubble impulse for three kinds of array explosions.

Table 5.Bubble parameter of underwater explosion between array charges and aggregate charge.

Table 6.Bubble periods of underwater explosion between array charges and aggregate charge.

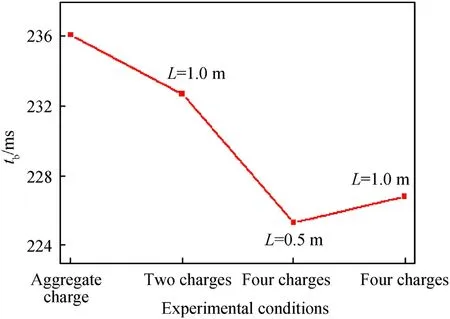
Fig.11.Bubble period of underwater explosion of aggregate and array charges.

5.Conclusions

The collision of multiple shock waves and bubbles leads to a complex power field of underwater array explosion.By adjusting the number of charges,the charge layout,and the array distance,the power field of underwater explosion can be adjusted,and the gain of the shock wave and bubble parameters in special position,and the cumulative damage effect on targets can be achieved.

(1) The interaction of underwater shock waves of equal strength can be equivalent to the reflection process of a shock wave on a rigid wall.The interaction of delayed shock wave can approximate the increase of the shock wave baseline.The impact (focusing) and delay superposition effects of the shock wave can increase its pressure peak.The greater the number of array explosion points is,the higher the impulse will be.

(2) Compared with the aggregate charge,the greater the number of explosion points,the higher the gain of the bubble peak pressure,and the smaller the array distance are,the higher the gain.However,the bubble impulse decreases significantly in all test conditions.Under the same array distance,the smaller the charge number is,the higher the bubble pulse impulse is.Under the same charge number,the smaller the array distance is,the higher the bubble impulse is.

(3) The bubble period decreases gradually with the increase in the number of charge,but the test orientation has little effect on the bubble period.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

I sincerely thank Researchers Wang Xuefeng,Researchers Ma Junli,Researchers Lu Zhongbao,Senior Engineer Li Qin,Senior Engineer Liu Yunzhou of the 705th Research Institute of China Shipbuilding Industry Corporation for their great help in experiments and testing.