Isogeometric analysis for free vibration of bidirectional functionally graded plates in the fluid medium

Quoc-Ho Phm ,Phu-Cuong Nguyen ,Vn Ke Trn ,Trung Nguyen-Thoi

aFaculty of Civil Engineering,Ho Chi Minh City Open University,Ho Chi Minh City,Viet Nam

b Faculty of Mechanical Engineering,Le Quy Don Technical University,Hanoi,Viet Nam

cDivision of Computational Mathematics and Engineering,Institute for Computational Science,Ton Duc Thang University,Ho Chi Minh City,Viet Nam

d Faculty of Civil Engineering,Ton Duc Thang University,Ho Chi Minh City,Viet Nam

Keywords:Contact plate-fluid Refined quasi 3D plate theory Mori -Tanaka model Isogeometric analysis Bidirectional functionally graded plate

ABSTRACT This paper for first time proposes an isogeometric analysis (IGA) for free vibration response of bidirectional functionally graded (BDFG) rectangular plates in the fluid medium.Material properties of the BDFG plate change in both the thickness and length directions via power-law distributions and Mori-Tanaka model.The governing equation of motion of BDFG plate in the fluid-plate system is formulated basing on Hamilton's principle and the refined quasi three-dimensional(3D)plate theory with improved function f(z).The fluid velocity potential is derived from the boundary conditions of the fluid-plate system and is used to determine the added mass.The discrete system of equations is derived from the Galerkin weak form and numerically analyzed by IGA.The accuracy and reliability of the proposed solutions are verified by comparing the obtained results with those published in the literature.Moreover,the effects of the various parameters such as the interaction boundary condition,geometric parameter,submerged depth of plate,fluid density,fluid level,and the material volume control coefficients on the free vibration behavior of BDFG plate in the fluid medium are investigated in detail.Some major findings regarding the numerical results are withdrawn in conclusions.

1.Introduction

In recent years,thanks to superior properties such as lightweight,high stiffness,capable of resisting high-temperature environments or extremely large temperature gradients,the functionally graded material(FGM) has been widely used in many engineering fields including mechanical,automotive,aero-space,civil engineering,and defense industry.Due to the abovementioned advantages and ample applications,the analysis of the mechanical behavior of the structures using the FGM has been investigated worldwide by many investigators[1-3].For example,Tahir et al.[4,5] and Menasria et al.[6] proposed the simple fourunknown theory to investigate the behavior of FG porous plates.Chakraverty and Pradhan [7] developed the Rayleigh-Ritz method basing on classical plate theory to investigate the free vibration of functionally graded plates with various boundary conditions.Zaoui et al.[8]used the novel shear strain shape function based on 2D and quasi 3D theories to study the free vibration of FGM plates resting on elastic foundations.Karami et al.[9] applied the second-order shear deformation theory to analyze the dynamic and buckling response of functionally graded carbon nanotube-reinforced composite plates on elastic foundation.Also,studying the FG plates resting on elastic foundation using an analytical approach was introduced in documents[10-12].Hachemi et al.[13]developed a new refined quasi-3D shear deformation theory and the concept of the neutral surface position to investigate the bending behavior of FG plates.Bakoura et al.[14] proposed a higher order shear deformation theory (HSDT) in conjunction with the stress function method to study the buckling behavior of FG plates.Bekkaye et al.[15] used the refined trigonometric shear deformation theory to analyze the mechanical response of FG porous plates.Rezaei et al.[16] presented the free vibration of FG plates based on the simple first-order shear deformation theory.Li et al.[17]proposed the new five-variable shear deformation theory to analyze the static bending behavior of FG plates.Nguyen et al.[18] developed the polygonal finite element method to investigate the static bending and vibration responses of FG porous plates with graphene platelets reinforcement.Kumar et al.[19] used the nonlinear FEM to study the vibration and transient response of FGP skew plates.Recently,Tran et al.[20-22] used the edge-based smoothed finite element method to study the static bending,vibration and dynamic behavior of FG porous plates.Also,Pham et al.[23]investigated the nonlinear static bending response of FGM shell and Tran et al.[24]studied the static and vibration behaviors of FG porous plates reinforced by graphene platelets.

Nevertheless,the structures made from the transverse FGMs or axial FGMs are not efficient enough for the applications in the aerospace,defense industry,or nuclear reactors when the temperature distributes differently along different directions.Thus,the multi-directional FGMs (MDFGMs) was proposed to meet these demands.To study the properties of MDFGMs,Karamanli and Vo[25] investigated the static bending behavior of two-dimensional FG microbeams under uniformly distributed loads using the quasi-3D model and modified couple stress theory.Li et al.[26]proposed the isogeometric analysis (IGA) based on the first-order shear deformation theory (FSDT) to analyze the static bending,free vibration and buckling responses of bi-directional FG porous plates.Also,Lieu et al.[27,28]employed the IGA based on NURBS to investigate the static bending,vibration and buckling responses of bi-directional FG plates and variable thickness plates.Wu and Yu[29] developed a finite annular prism method to analyze the free vibration response of bi-directional FG annular plates.

The structures in the fluid medium have been applied in various fields such as nuclear,ocean,naval engineering and defense industry.Therefore,a clear understanding of the behavior of the structures in the fluid medium is necessary and has been studied widely by many researchers.Cho et al.[30,31] proposed an analytical approach to study the free vibration and forced vibration of plates and stiffened panels contact with fluid on one side.Hashemi et al.[32] developed the Ritz method to analyze the free vibration of vertical plates resting on the foundation in contact with fluid on one side.Watts et al.[33] proposed the semi-analytical method that relied on the Galerkin to investigate the vibration response of the non-rectangular bottom of tanks filling with liquid.Bendahmane et al.[34] employed the hierarchical finite element method based on the higher-order shear deformation theory to study the natural frequency of composite plates with variable stiffness submerged in fluid.Khorshidi et al.[35-37] used the Rayleigh-Ritz method with finite Fourier series to determine the natural frequencies of square plates in contact with a bounded fluid.In this study,they examined different materials of plates such as isotropic,laminate composite,and functionally graded materials.

The isogeometric analysis(IGA)proposed by Hughes et al.[38],which combines computer-aided design and finite element analysis,has been developed by many researchers for its advantages and effectiveness.The essential idea of the isogeometric analysis is to employ the same basis functions to exactly describe the geometry domain,as well as to approximate the unknown fields.Since the geometry is exactly modelled and the number of unknown terms does not increase,it is expected that the IGA would yield more accurate results with lower computational cost for plate problems using HSDT or refined higher-order shear deformation plate theory (RPT) in the comparison with other numerical methods such as finite trip method,finite element method,or meshfree method,etc.The IGA has been developed for analyzing many different structures such as analysis beams [39-46],plates[47-55] and shells [56-63].Most of the works have given the conclusion that the IGA has high accuracy and can be extended relatively easily for complex structures.In particular,thanks to satisfying higher-order derivatives of NURBS functions and the suitability to use the elasticity nonlocal theory,the IGA has been applied in many nanostructures such as nanobeams [64,65],nanoplates[66-74]and nanoshells[75,76].However,based on the updated knowledge of the authors,the analysis of the structures in the fluid medium by using the IGA is still limited.

As observed from the above literature reviews to the authors'best knowledge,the investigation on the free vibration of the FGM plates in the fluid medium using the IGA has not yet been studied.This paper is hence performed to fill in this research gap by proposing an IGA for free vibration analysis of bi-directional functionally graded(BDFG)rectangular plates in the fluid medium.The plates are considered in the fluid medium including the cases of the plate in horizontal or vertical positions and the plate in full or partial contact with fluid.The material properties are assumed to change continuously in both the thickness and length directions according to a power-law distribution and using Mori-Tanaka model.Hamilton's principle and the refined quasi threedimensional (3D) plate theory with improved function f(z) are used to set up the governing equation of the BDFG plate in the fluid medium.The discrete system of equations is derived from the Galerkin weak form and numerically analyzed by the IGA.The obtained numerical results are compared with other published works in literature to demonstrate the accuracy and reliability of the proposed method.In addition,the influences of the various parameters such as the interaction boundary condition,geometric parameter,and material volume control coefficients on the free vibration response of BDFG plates in the fluid medium are also examined.The present work helps to add physical data and laws in the design and manufacture of structures in engineering fields such as maritime and aviation.Further more,the results of present work can be applied in the defense fields such as fuel tanks,submarines,warships,underground structures in the ocean,military structures on the seas and islands,cooling areas of furnaces nuclear reactions,etc.

For the convenience of readers,the sections of the article are arranged as follows: Section 1 is a general introduction.Section 2 introduces the theoretical formulation.Section 3 presents the NURBS functions and IGA for free vibration of BDFG plates in the fluid medium.Section 4 presents the numerical results to demonstrate the accuracy and reliability of the proposed method.Finally,some major conclusions are withdrawn in Section 5.

2.Theoretical formulation

2.1.Model of bidirectional functionally graded rectangular plates

We consider a rectangular BDFG plate has the length a,the width b and the thickness h,which is made from a mixture of ceramics and metals as shown in Fig.1.The material properties are assumed to change continuously from a top surface(z=+h/2)to the bottom surface (z=-h/2) according to a power-law distribution.The volume fraction of ceramic Vand metal Vvaries in both the thickness and length directions according to the law of:

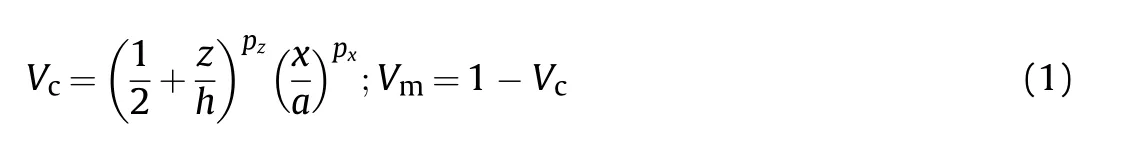
where pand pare the non-negative axial and transverse powerlaw indexes,which determine the material distribution in the length and thickness directions of the plate,respectively.

Two micromechanical models,namely the Voigt model and Mori-Tanaka scheme are employed herein to evaluate the effective material properties of the BDFG plate.An effective property P(x,z)such as elastic modulus and mass density evaluated by the Voigt model is of the form:

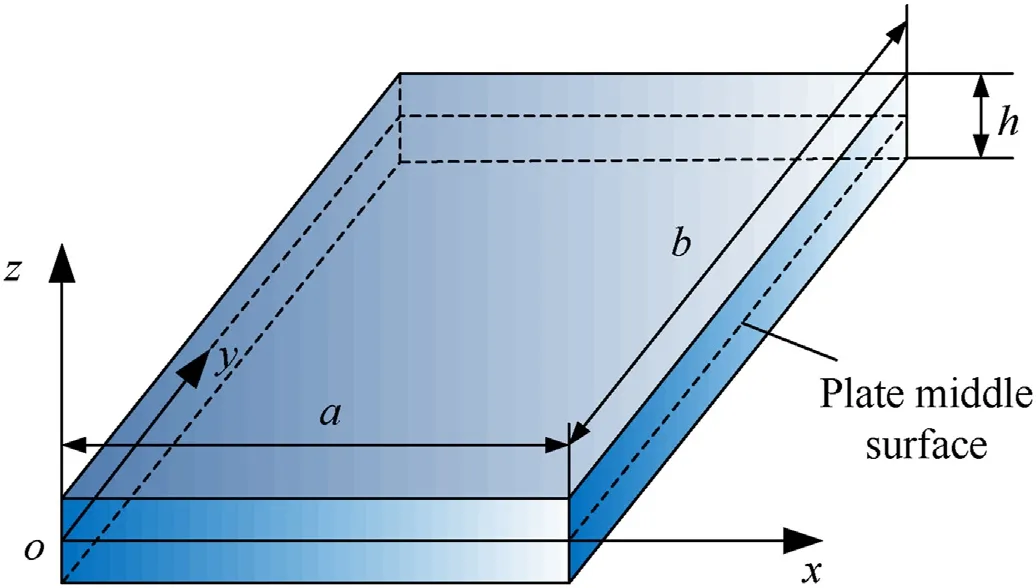
Fig.1.Model of a bi-directional functionally graded (BDFG) rectangular plate.

where P is the effective material property such as Young's modulus E,mass density ρ,and Poisson's ratio v;subscripts m and c denote the metallic and ceramic constituents,respectively.

According to the Mori-Tanaka scheme (Mori and Tanaka [77]),the effective bulk modulus Κand shear modulus Gat any point of the plate are given by:

The effectiveness of Young's modulus E and Poisson's ratio υ are computed via the effective bulk modulus and shear modulus as follows.

Noting that the effective mass density ρ is defined by Voigt model according to Eq.(2)

with p=p=2;the Young's modulus E by Mori-Tanaka and the mass density ρ through the thickness z and the length x of BDFG plate are shown in Fig.2.

2.2.The refined BDFG plates model

According to the refined higher-order shear deformation theory(HSDT),the displacement field of the plates by(Mantari and Soares[78]) is defined by:

where U,U,Uare the displacements in the x,y,and z directions,respectively;Uand Vare respectively the in-plane displacements of the middle surface;Wand Ware the bending and shear components of the transverse displacement,respectively;f(z)and g(z)are the functions in the form of

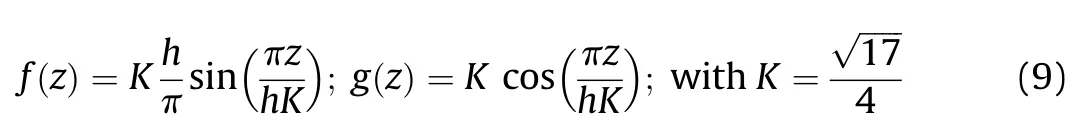
The linear strain components of the BDFG plate are written based on the displacements field in Eq.(7) by:

In Eqs.(14) and(15),it can be seen that the components of the transverse shear strains γ,γare equal to zero on top (z=h/2)and bottom surfaces (z=-h/2) of the BDFG nanoplate.The strain fields of BDFG plate can be briefed in vector forms as follows:

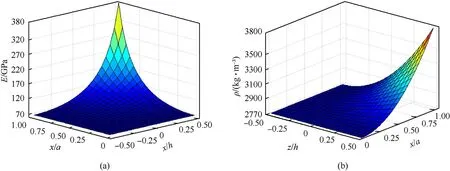
Fig.2.Variation of Young's modulus Mori-Tanaka (a) and mass density (b) through the thickness and the length of the plate for pz= px=2.

in which Care given by:

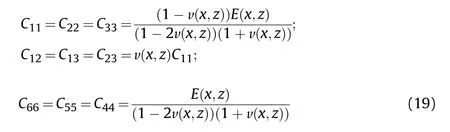
2.3.Fluid model

In the present work,the fluid dynamic pressure acting on the plate is expressed as a function of acceleration with the following assumptions (Soni et al.[79]):

1.The fluid flow is homogeneous,incompressible,inviscid and norotation motion.

2.The fluid flow is small and hence the amplitude of vibration complies with the small deflection theory.

3.The fluid is assumed to be non-viscous,and hence the fluid pressure impacting on the plate is completely normal to the plate surface.

4.The influence of boundary conditions on the number of a plane wave is neglected.

5.The length of the plate is smaller than the level of fluid below the plate,and hence the rigid bottom of the fluid container does not affect the dynamics of fluid-plate.

6.The plate in-plane dimensions are smaller than the length and width of the container,and hence the walls of the container do not participate in the vibrations of the plate in contact with the fluid.

7.The effect of the non-linearity at the interface of the fluid-plate is neglected.

8.The thickness of the plate is thin,and hence the formulation of in-plane forces can neglect the effect of fluid forces.

The BDFG rectangular plates with the fluid dynamic pressure are modelled for the case of the horizontally submerged plate as shown in Fig.3,and for the case of the vertically immersed plate as shown in Fig.4.For both the horizontal and vertical configurations,this section derives a general differential equation governing the velocity potential as

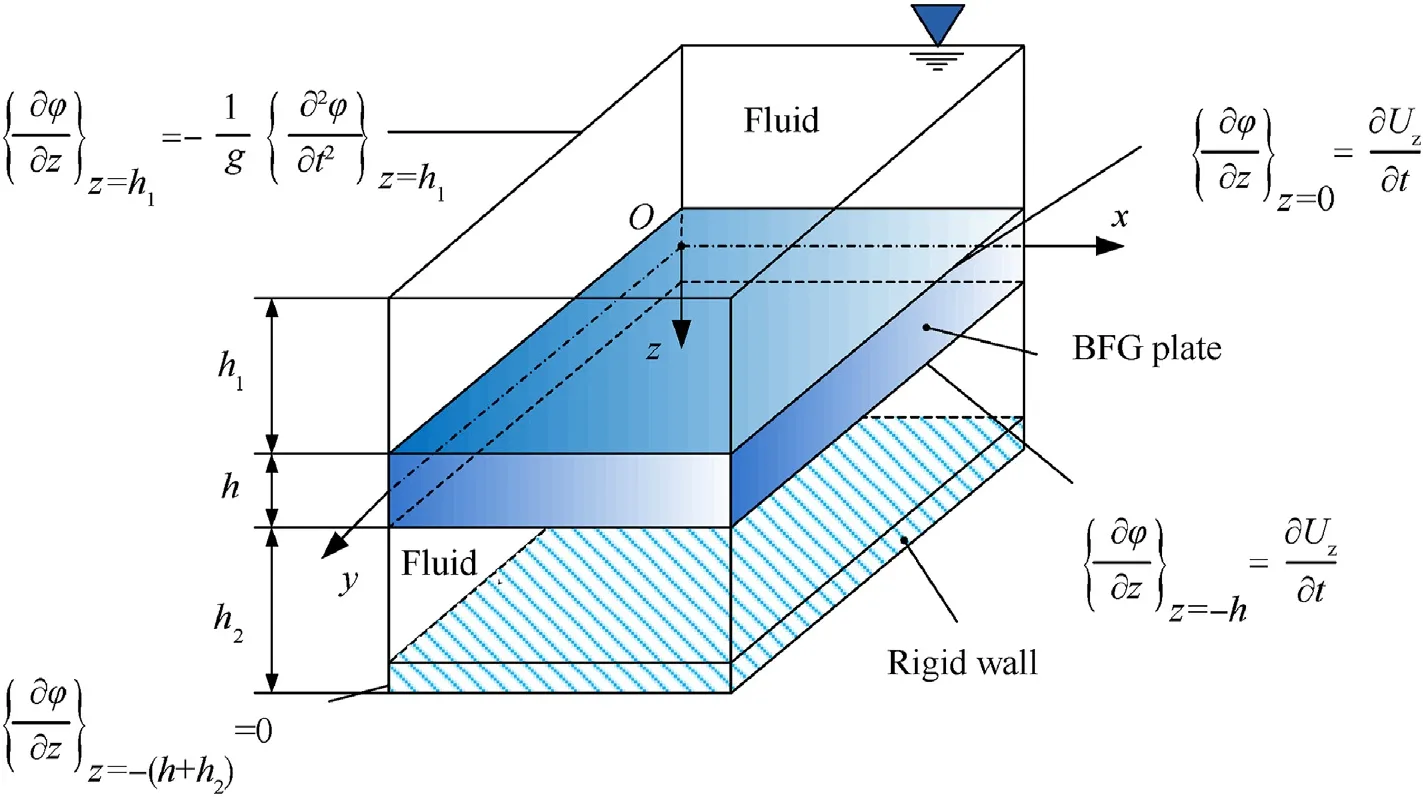
Fig.3.Plate-fluid model bounded by a rigid wall.

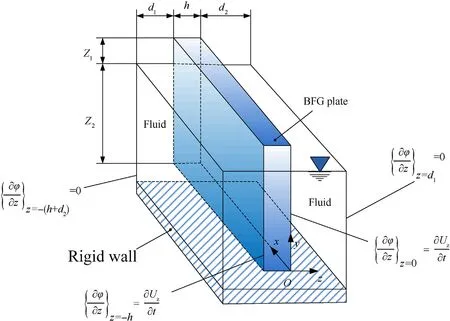
Fig.4.Vertical plate partially submerged in a fluid tank.

The boundary conditions for the horizontal and vertical plates are then dealt with separately.Using Bernoulli's equation and neglecting its nonlinear terms,the fluid pressure at any point of the fluid-plate interface can be expressed as:

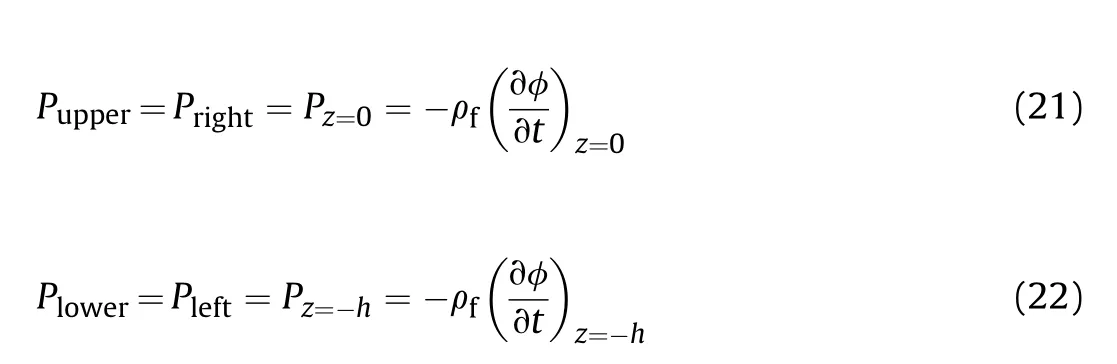
where ρis the fluid mass density.

The following separate variable relation is assumed for the potential velocity function:

where F(z) and Q(x,y,t) are two separate functions needing to be determined from fluid boundary conditions.It is assumed that for a permanent contract that exists between the plate surface and peripheral fluid layer,the out-of-plane velocity component of the fluid on the plate surface should match the instantaneous rate of change of the plate displacement in the transverse direction.So at the fluid-plate interfaces,the upper/right plate-fluid interface and lower/left plate-fluid interface,can be expressed,respectively,by the following kinematic boundary conditions

Substituting Eq.(23) into Eqs.(24) and (25),one obtains the relationship between two separated functions of the velocity potential as:

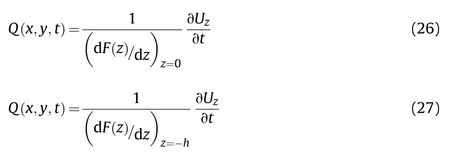
The velocity potential on fluid-plate interfaces can be expressed by substituting Eqs.(26) and (27) into Eq.(23) as

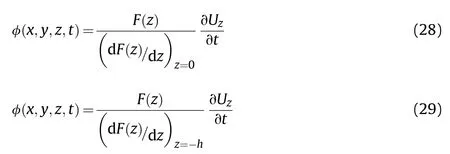
Eq.(20) can now be recast in terms of the lateral deflection of the plate by introducing Eqs.(28) and (29).The resulting secondorder general differential equation can be written as

Substituting Eq.(31) into Eqs.(28) and (29),one obtains the expression for the velocity potential function on the fluid-plate interface as follows:

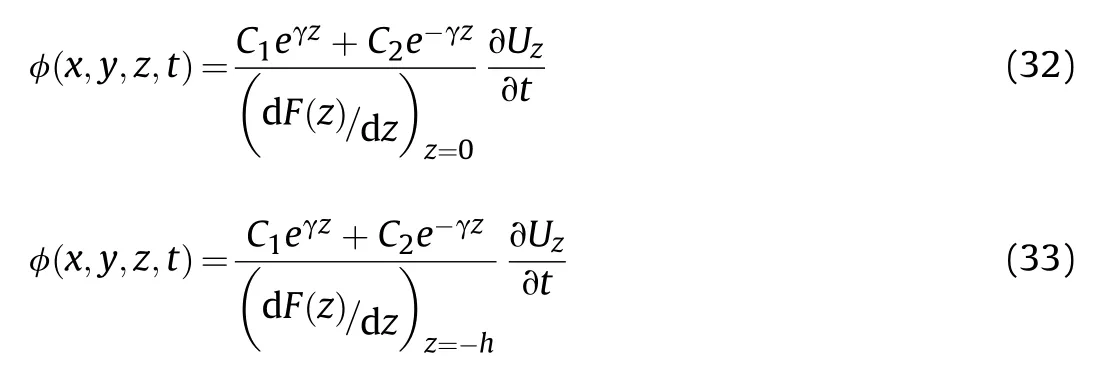
where C,Care the integral constants determined according to contact boundary conditions between the fluid and the plate.

2.3.1.Dynamic pressure for horizontally submerged plate

For the case of the horizontally submerged plate (Fig.3),the fluid extreme boundary conditions include the free fluid surface at z=hand the rigid bottom surface at z=h+h.Thus,the potential function corresponding to the boundary conditions is determined by:

For the free fluid surface:

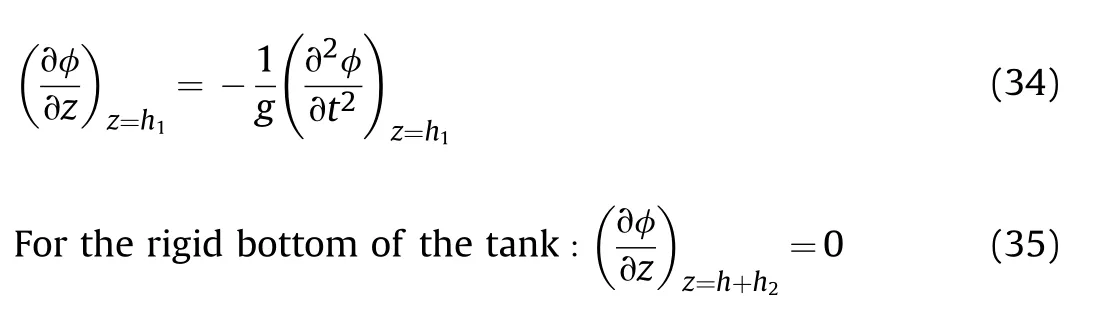
where g represents the gravity acceleration.

Considering the velocity potential φas a function of sinusoidal time dependence:

Substituting Eq.(36) into Eq.(34),we obtain

Substituting Eq.(31) into Eq.(37),we obtain

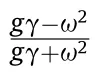
Similarly,substituting Eq.(32) into Eq.(24),one finds

From Eqs.(38) and (39),we obtain the results

Substituting Eq.(40) into Eq.(32),we get the required relation for the potential function of the fluid on the upper portion of the plate as

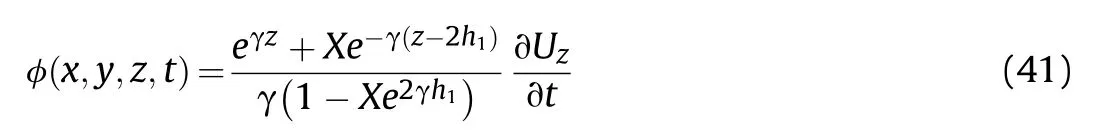
Similarly,by substituting Eq.(33)into Eqs.(35)and(25),we get the required relation for the velocity potential function of the fluid in the lower portion of the plate as

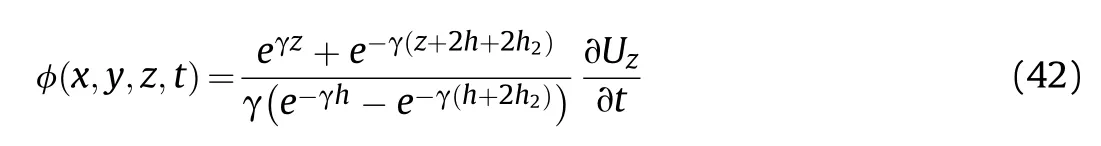
Substituting Eq.(41) into Eq.(21),the fluid dynamic pressure acting on the upper surface of the plate can be expressed as

Similarly,substituting Eq.(42) into Eq.(22),the fluid dynamic pressure acting on the lower surface of the plate is expressed as

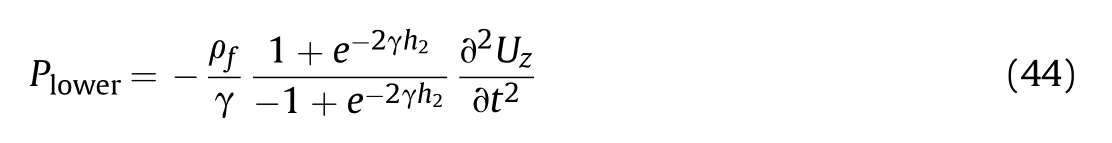
Now,the difference of the fluid dynamic pressure between the upper and lower surfaces ((ΔP) for the horizontally submerged plate can be written as

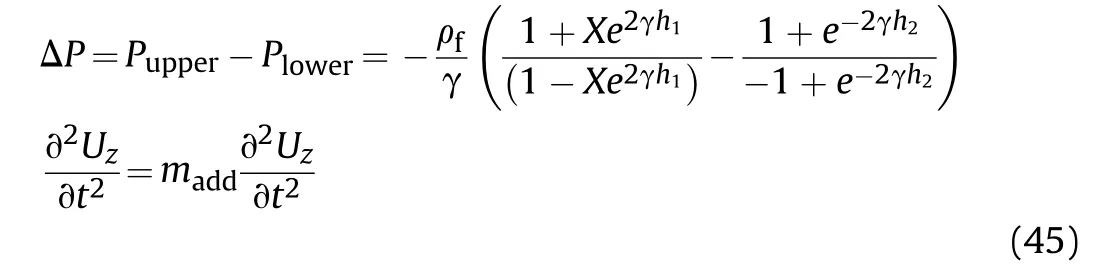
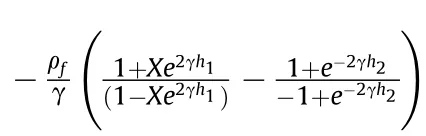
2.3.2.Dynamic pressure for vertical submerged plate

For the case of vertical plate partially immersed in fluid as shown in Fig.4,the difference of the dynamic pressure ΔP of surrounding fluid may be expressed as:

where P,Pare the fluid dynamic pressures acting to the right and left surfaces of the plate.The boundary conditions for the fluidplate interface on left and right ends are given by:

From Eqs.(24),(32) and (47),the expression for velocity potential function on the right side of the plate becomes

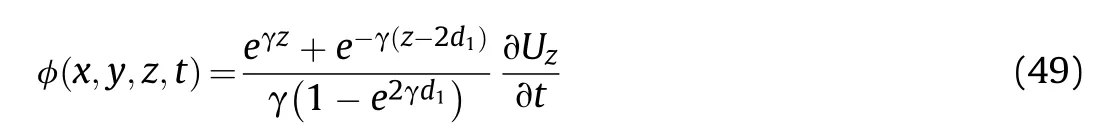
Similarly,from Eqs.(25),(33) and (48),the expression for velocity potential function on the left side of the plate becomes

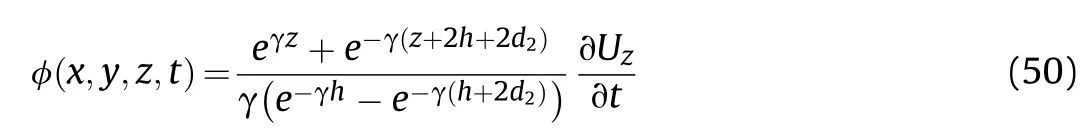
From Eqs.((22),(46),(49) and (50),the total difference of the dynamic fluid pressure ΔP for vertically submerged plate conditions is expressed as

2.4.The governing equation

The equations of motion of the BDFG plate in the fluid medium are based on the refined three-dimensional plate theory derived from Hamilton's principle by:

where δU,δW and δT are the variation of the strain energy,external work and kinetic energy.The variation of the strain energy can be given by:

The variation of external work can be expressed as:

where ΔP is the hydrodynamic pressure of fluid,perpendicular to the plate surface and presented in sections 2.3 and Eq.(57)can be written as

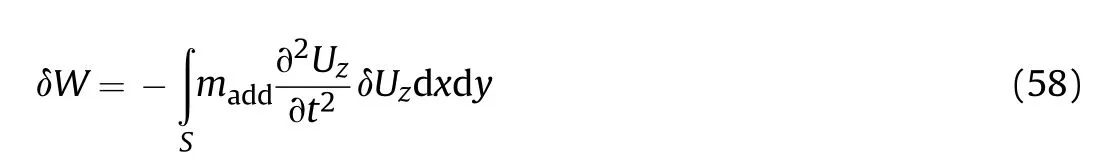
The variation of kinetic energy is given by:

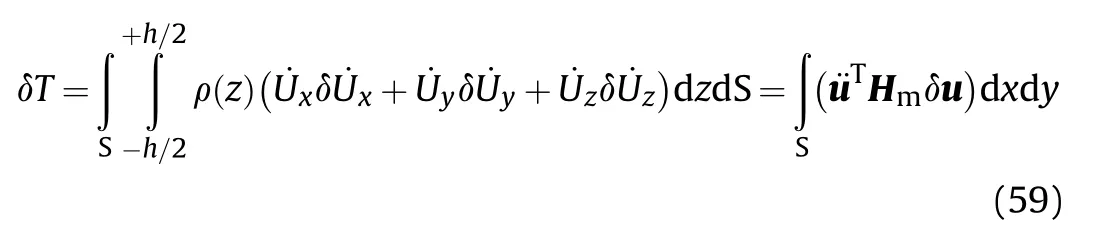
Substituting Eqs.(53),(57)and(59)into Eq.(52),a weak form of the plate in fluid medium can be described as:

3.NURBS -based IGA for free vibration analysis of plates in the fluid medium

3.1.NURBS basis functions

In the IGA,the knot vector k(ζ)is defined as the nondecreasing numbers between zero and one k(ζ)={ζ=0,…,ζ,…,ζ=1},where i represents the knot index;ζis called the iknot;n is the number of basic functions,and p is the order of the polynomial.The univariate B-spline basis function N(ζ),is defined recursively by(Hughes et al.[38]):

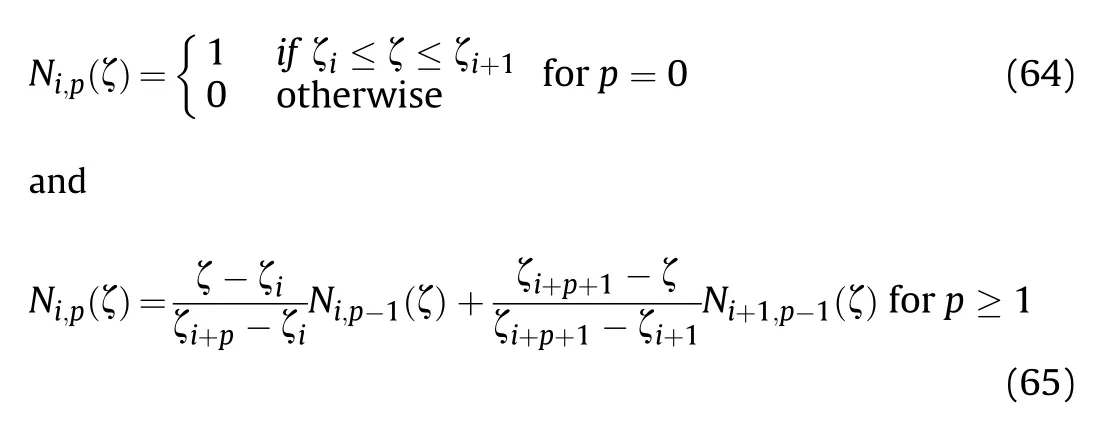
Two-dimensional NURBS basis functions can be constructed by taking the tensor product of the univariate B -spline basis functions in two parametric dimensions ζ and η

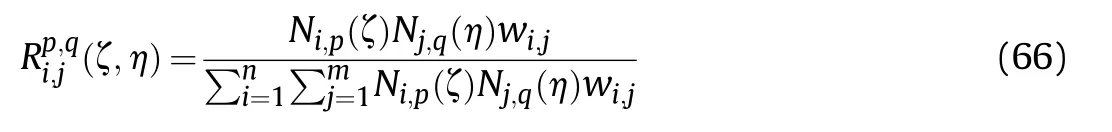
where ware the weight;N(ζ) and N(η) represent the B -spline basis functions of order p in the ζ and order q in the η direction,respectively;N(η)follows the recursive formula shown in Eq.(65)with knot vector k(η),which is defined in the same manner as k(ζ).

3.2.NURBS based formulation

The displacements in the middle plane of the plate are approximated as follows:

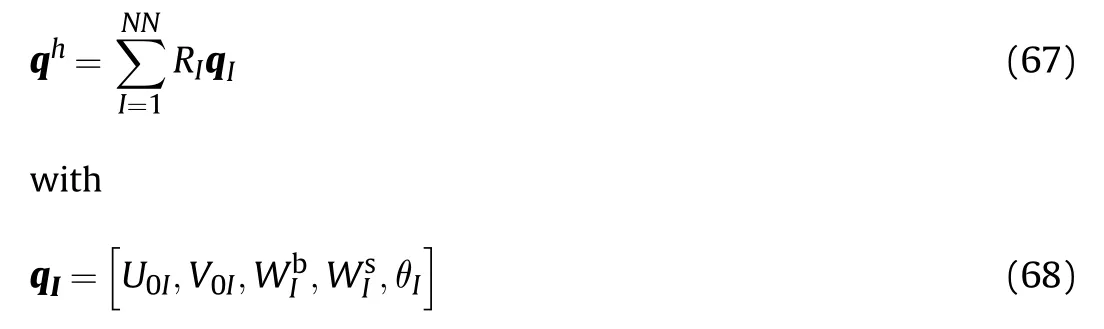
where NN=(p+1)(q+1) is the number of control points per physical element;Rand qdenote the shape function and the unknown displacement vector at control point I,respectively.

The displacements U,V,W,W,θ are written in matrices as follows:

Substituting Eqs.(69)-(73)into Eq.(17),the in-plane,shear and normal strains can be rewritten as

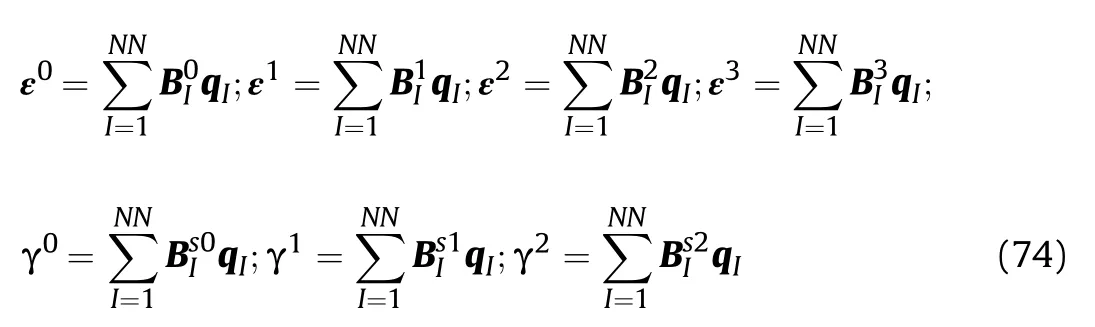
in which

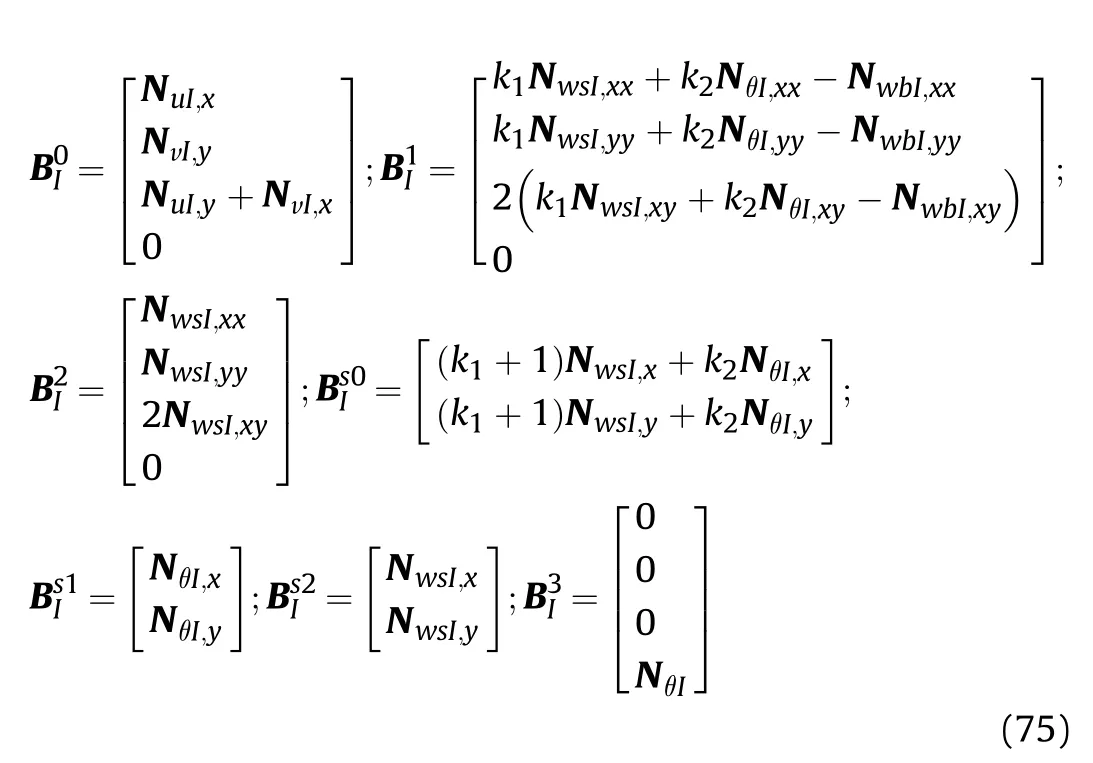
Substituting Eqs.(69)-(73)into Eq.(60),the displacement field u is obtained as:

Substituting Eqs.(76)-(78)into Eq.(63),the matrix form of the global equilibrium equations for the free vibration analysis of the BDFG plates in the fluid medium is determined by

where M,Mare the mass matrix of the plate and the mass matrix of fluid-plate:

in which,ω is the natural frequency value.

4.Numerical examples

In this section,some numerical results are performed by usingMatlab's codes based on the proposed theoretical formulation for BDFG plates submerged in the fluid medium.The (p+1)(q +1)Gaussian quadrature is adopted for two-dimensional elements,where p and q represent the orders of the NURBS basis function along the ζand η directions in the parametric domain,respectively(Hughes et al.[38]).In order to demonstrate the accuracy of the present IGA models,the comparative analyses of vibration are given as

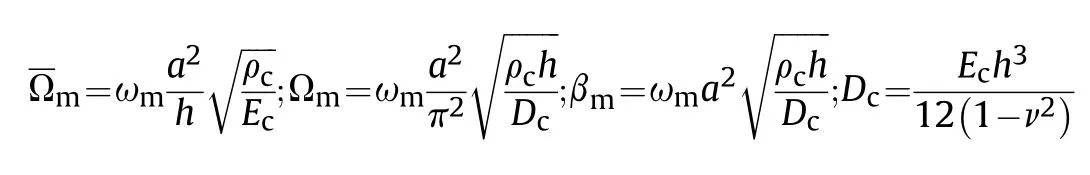
in which m is the m-th natural frequency;and the material properties of BDFG plate are given in Table 1.

Table 1.Mechanical properties of the BDFG plate ([26,82]).

Table 2.Comparison of dimensionless frequencyof the Al/Al2O3 rectangular plate with the SSSS boundary condition.

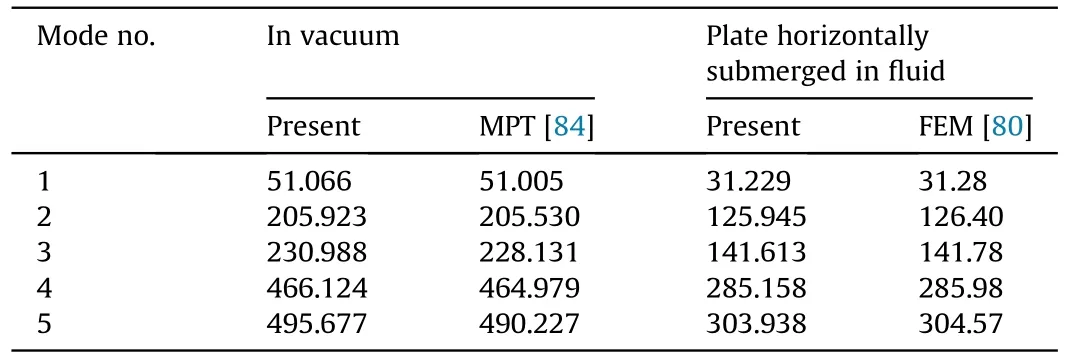
Table 3.Comparison of the natural frequencies ω(Hz) of the horizontally FG plate(with the SFSF boundary condition) in a vacuum and submerged in fluid.

The obtained numerical results of the present work are compared with the following approaches:

· Quasi 3D -IGA: The higher-order Quasi 3D and isogeometric analysis (Nguyen et al.[82]).

· RPT -IGA: Refine higher-order shear deformation plate theory and isogeometric analysis (Nguyen et al.[82]).

· TSDT-Navier's: Third-order shear deformation plate theory and Navier's method (Thai and Kim [83]).

· MPT: Mindlin's plate theory and exact-closed form characteristics equation (Hosseini-Hashemi et al.[84]).

· FEM:Classical plate theory and finite element method(Kerboua et al.[80]).

· FSDT-IGA: First-order shear deformation plate theory and isogeometric analysis (Li et al.[26]).

· Present: refined quasi 3D plate theory and isogeometric analysis.

4.1.Validation study

Fig.5.The mesh of 20 × 20 control points for a square plate.

Next,let us consider the FG plates horizontal submerged in the fluid medium.The dimensional parameters and material properties of FG plates include Young's modulus E=207 GPa,material density ρ=7850 kg/m,Poisson's ratio=0.3,a=0.655,b=0.20165 and thickness h=9.36 mm.The fluid density is taken by 1000 kg/m.The plate is horizontally submerged in a rectangular reservoir tank with dimensions of 1.3 m×0.55 m×0.8 m.Table 3 presents the natural frequencies of two opposite sides of the FG plates (with the SFSF boundary condition) in a vacuum and horizontally submerged in fluid.It is seen that the obtained numerical results by the proposed method agree well with the results of the exact solution obtained by Mindlin's plate theory (Hosseini-Hashemi et al.[84]) in the vacuum and by the finite element method(Kerboua et al.[80])when completely submerged in fluid.

Table 4 presents the numerical results of the first two frequencies of FG plates horizontally submerged in a fluid with different fluid levels of the present method compared with the exact solution (Hosseini-Hashemi et al.[84]).It can be found that the obtained results of the present method agree well with those obtained by published work (Hosseini-Hashemi et al.[84]).In particular,in view of Table 4,it is observed to gain the expected results for all boundary conditions:the increase of submerged fluid levels leads to the decrease of frequencies of FG plates.It is also noted that the frequencies of FG plates only decrease slightly whenthe plate is submerged in a fluid with the level.h/ a ≥0.3.

Table 4.Comparison of the first two frequencies of the plate horizontally submerged in a fluid with various fluid levels.

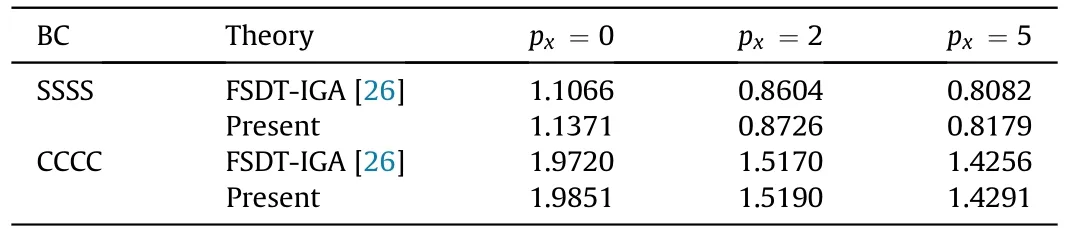
Table 5.Comparison of the first non-dimensional frequency Ω1 of the Si3N4/SUS3O4 square BDFG plates with the SSSS and CCCC boundary conditions(a=1,h/a=0.1,pz=1).

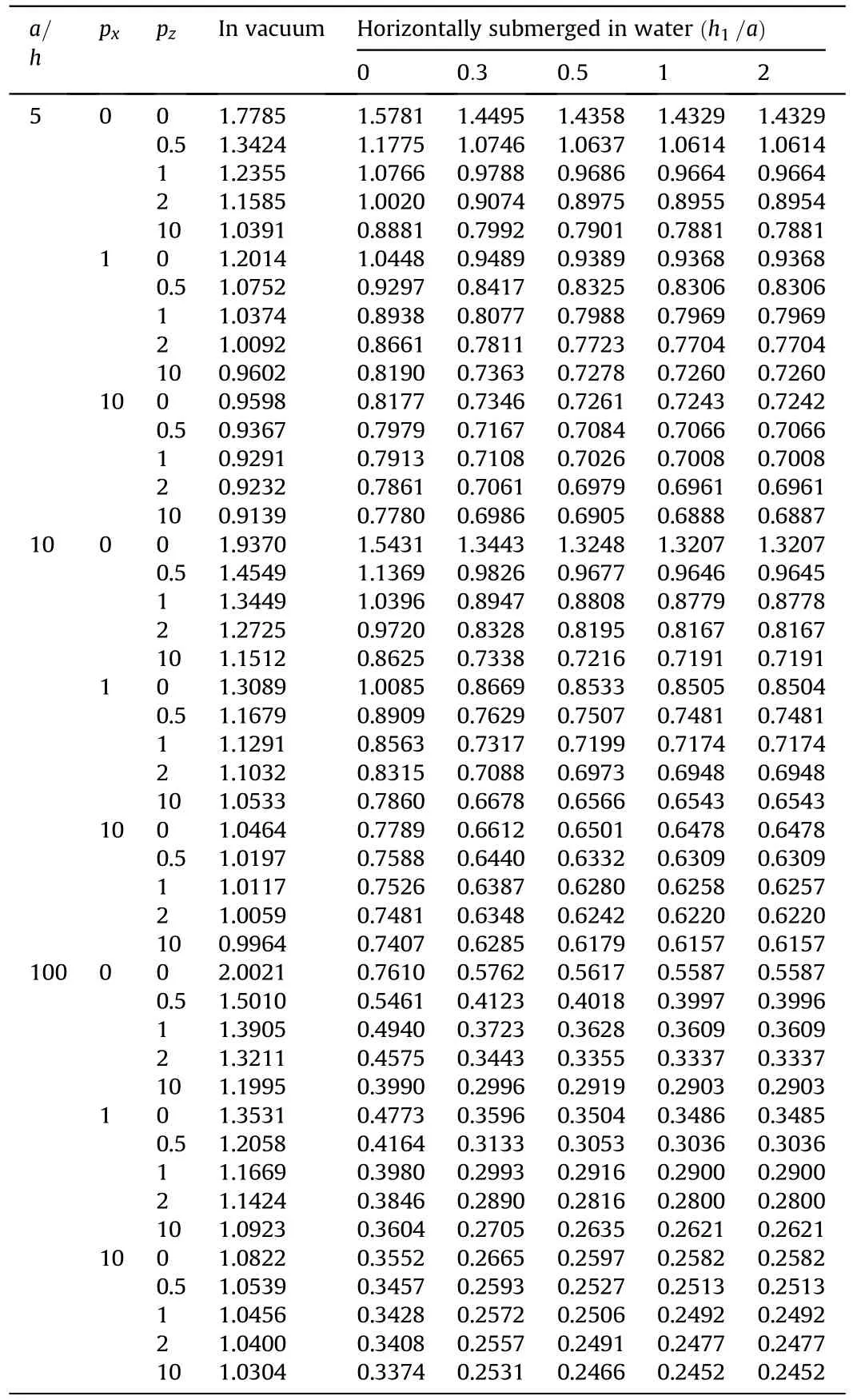
Table 6.The non-dimensional frequency Ω1 of the Al/Al2O3 square BDFG plates (with the SSSS boundary condition) horizontally submerged in the water.

Lastly,we consider the cases of the SiN/SUSOsquare BDFG plates with the simply supported and full clamped boundary conditions and with material parameters given in Table 1.Table 5 presents the numerical results of the first dimensionless natural frequencies of BDFG plates of the present method compared to those of published work(Li et al.[26]).It is seen that there is a good agreement between the results obtained by the proposed method and those by the IGA of Li et al.[26].However,the results by the IGA of Li et al.[26] are slightly smaller than those by the proposed method.It is because the IGA of Li et al.[26] only used the FSDT theory,while the IGA in the present work uses the refined quasi 3D plate theory.The above-compared examples hence verified the accuracy and reliability of the proposed approach.

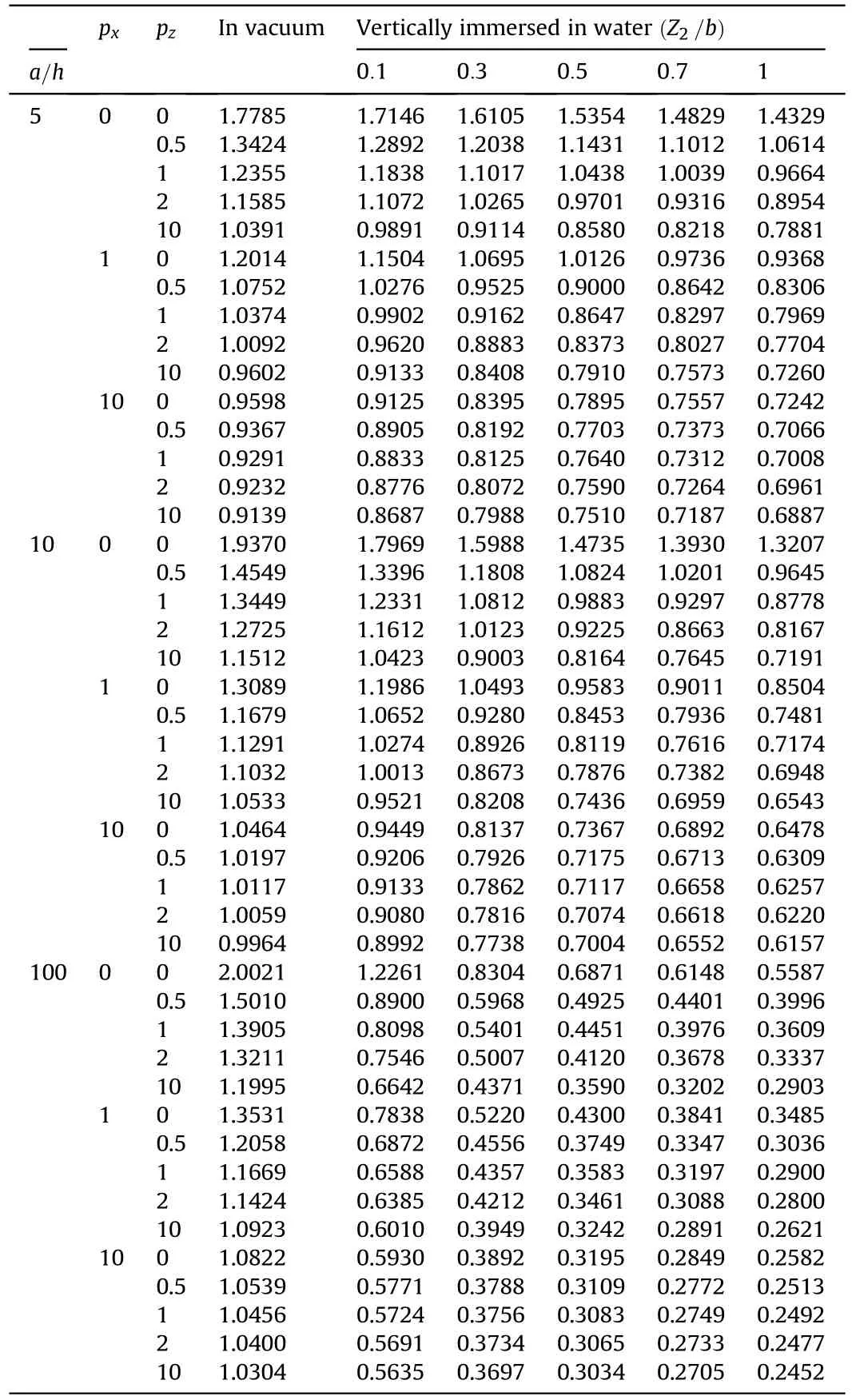
Table 7.The non-dimensional frequency Ω1of the Al/Al2O3square BDFG plate(with the SSSS boundary condition) vertically immersed in the water (d1= d2).

4.2.Numerical results and discussion

In this section,the influences of different geometric and material parameters (such as the length-to-thickness ratio,width-tolength ratio,power-law indexes),different models of plate submerged in fluid,and different boundary conditions on the natural frequencies of BDFG plates are conducted.The square plate has thegeometric parameter a=1 m,and the dimension of tank 5 × 5 × 5 m.The numerical results are presented in tubular and figure forms.

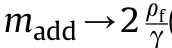
Table 8.The first five non-dimensional frequencies Ωmof Al/Al2O3 square BDFG plate horizontally submerged in the water (a=1; h/a=0.2, px=1, pz=1).

The effects of the length-to-thickness ratio a/h,the power-law indexes p,pand the fluid depth level to length ratio Z/ bon the natural frequencies Ωof the Al/AlOsquare BDFG plate (with the SSSS boundary condition) vertically immersed in the water are reported in Table 7.It can be observed that the increase of fluid depth level to length ratio Z/bmakes the natural frequency Ωdecrease continuously until the vertical plate is completely submerged in the water.It is noted that the natural frequency Ωare the same when the vertical plate and the horizontal plate are completely submerged in the water.

Table 8 and Table 9 present,respectively,the influence of the boundary conditions:CCCC,CCCS,CSCS,CFCF,SSSC,SFSS,and SFSF on the first five frequencies of the plate horizontal submerged in the water(h/a)and the plate vertical partially in contact with the fluid Z/b .Similar to the behavior of plates in a vacuum,the natural frequency Ωof the plates submerged in the water gains the maximum value with the CCCC boundary condition and the minimum value with the SFSF boundary condition.

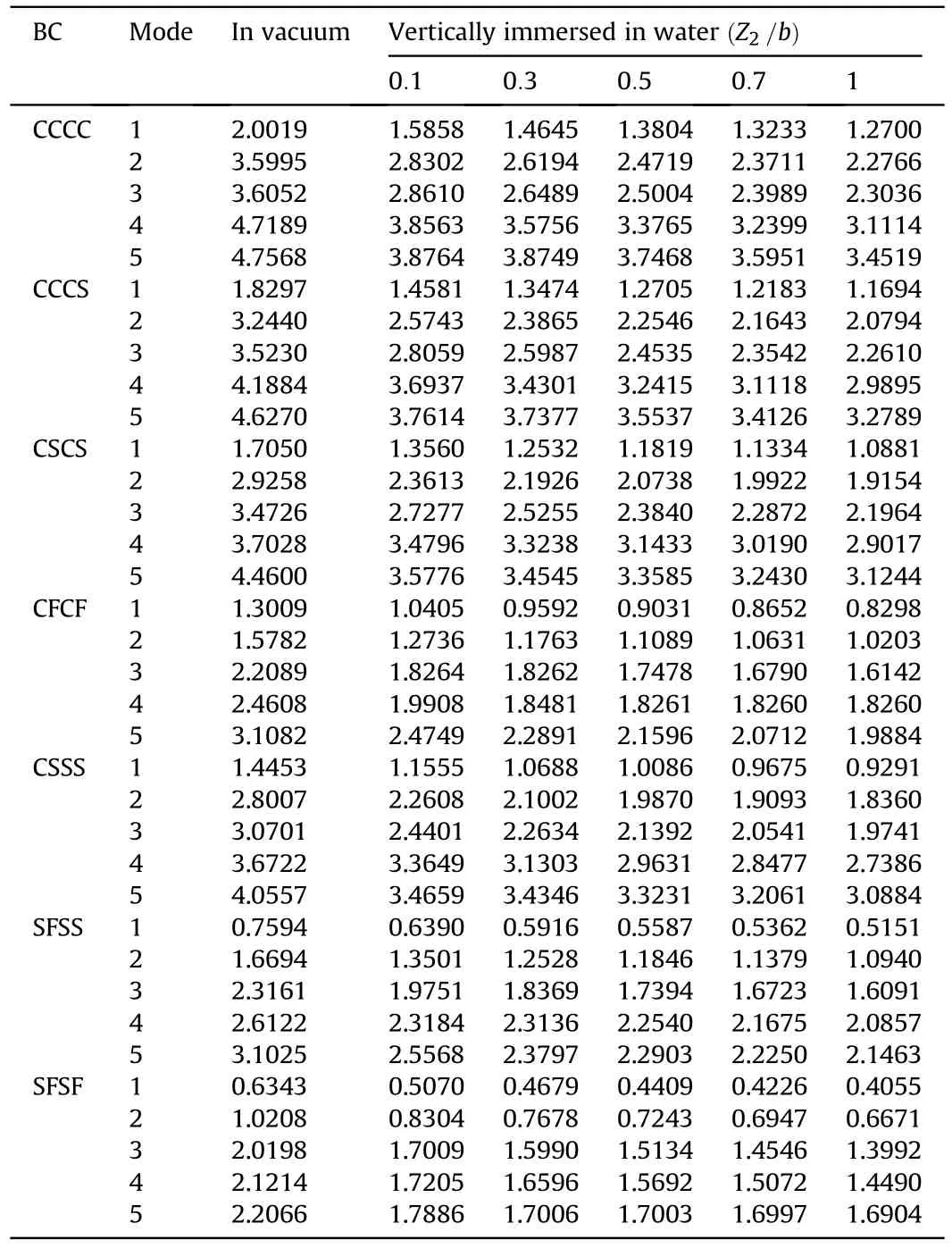
Table 9.The first five non-dimensional frequencies Ωm of Al/Al2O3 square BDFG plate vertically immersed in the water(a=1; h/a=0.2, px=1, pz=1).

Fig.6 and Fig.7 depicted,respectively,the first six modes of the Al/AlOsquare BDFG (with the SSSS boundary condition) plate horizontally submerged in the water and of the Al/ AlOsquare BDFG(with the SFSF boundary condition)plate vertically immersed in the water.It can be seen that similar to plate structures in vacuum or air,the results of the shapes and values of modes 2 and 3 aresimilar in the SSSS boundary conditions.This phenomenon is also the same for the modes 5 and 6.Fig.8 illustrate the effect of the length to thickness on the dimensionless natural frequency Ωof BDFG plates in contact with the fluid.From Fig.8,it can be observed that when the length to thickness ratio a/h=2,the natural frequency Ωin vacuum and fluid are the same.However,when the length to thickness ratio of the plate increases,the natural frequency of the plate in vacuum increases to a maximum value and then decreases for the plates submerged in fluid and the attenuation rate of the horizontal plate is faster than the vertical plate in the fluid medium.Moreover,the vertical plate in the fluid has a higher value of the natural frequency than those of the horizontal plate in the fluid.

The effects of the width-to-length ratio b/aon the natural frequency Ωof the BDFG plates are plotted in Fig.9.It can be observed that the length to width ratio b/a changing from 0.5 to 3 makes the natural frequency Ωincrease rapidly in all three cases:plate in a vacuum,plate horizontally submerged in the water and plate vertically submerged in the water.In addition,when the ratio b/a is larger,the difference between the natural frequency of horizontal and vertical plates in the fluid medium also become larger.However,the horizontal plate in the fluid medium always gives a smaller natural frequency.

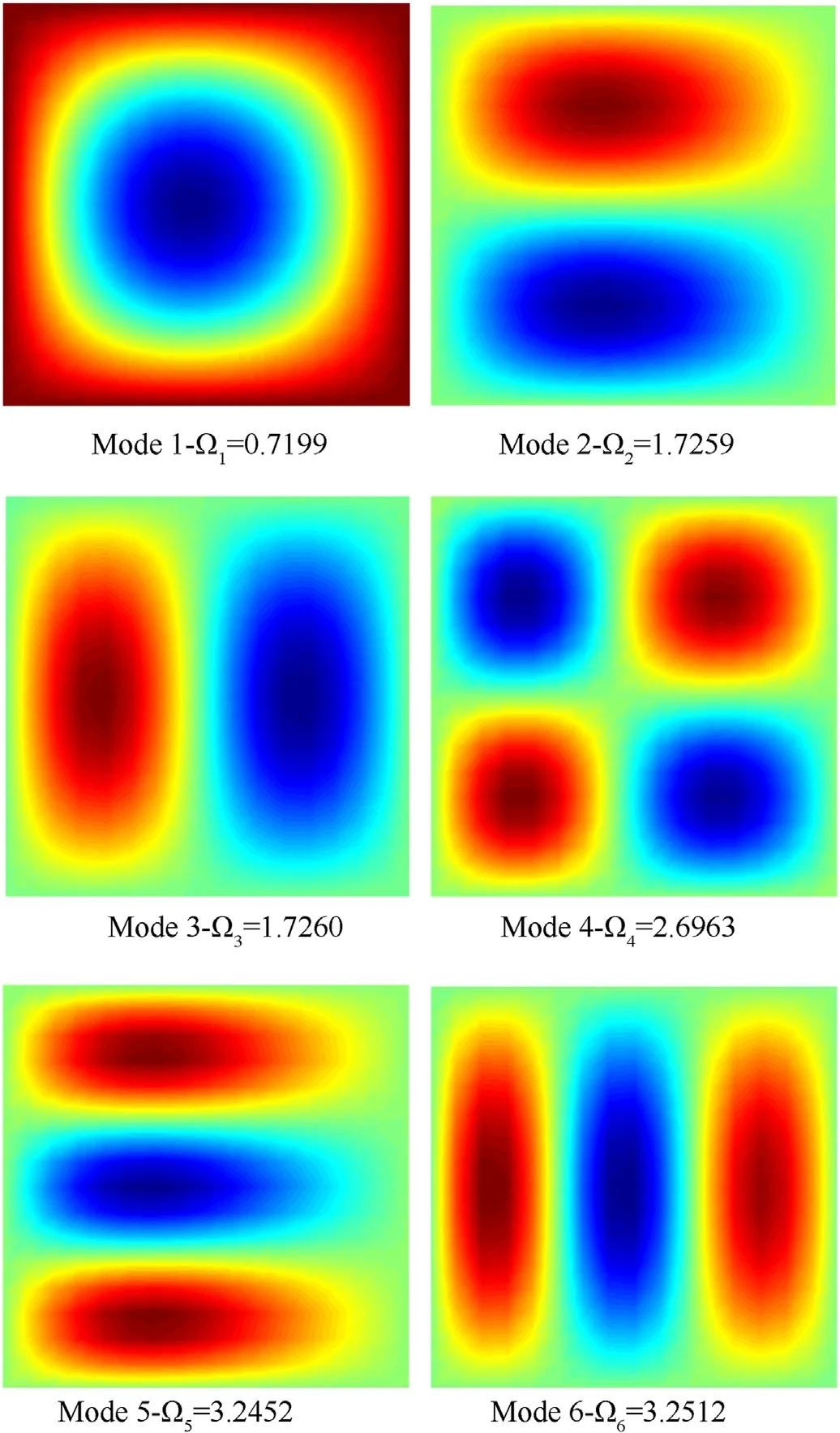
Fig.6.The first six free vibration modes of the Al/Al2O3 square BDFG plate (with the SSSS boundary condition)horizontally submerged in the water(a=1; h/a=0.1, px=1, pz=1,h1=0.5a).

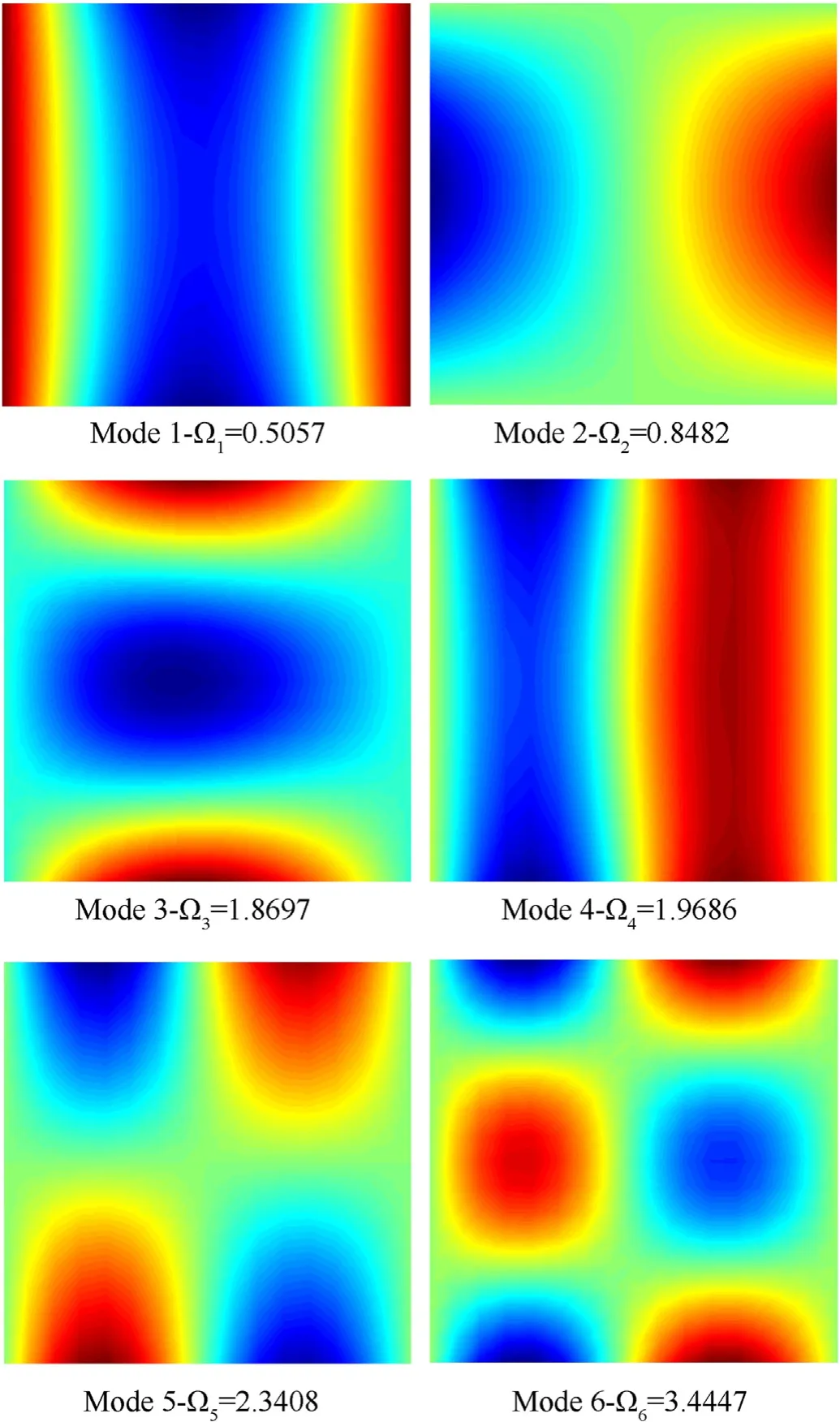
Fig.7.The first six free vibration modes of the Al/Al2O3 square BDFG plate (with the SFSF boundary condition) vertically immersed in the water(a=1; h/a=0.1, px=1,pz=1,Z2=0.5b).

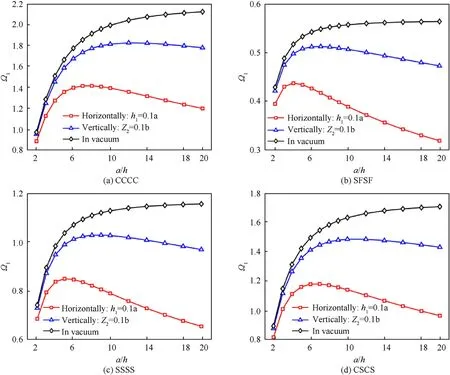
Fig.8.Effect of the various length to thickness ratio a/hon the dimensionless natural frequency Ω1 of the Al/Al2O3 square BDFG plate(a=1, px=1, pz=1,d2=d1)with different boundary conditions: a) CCCC;b) SFSF;c) SSSS;d) CSCS.

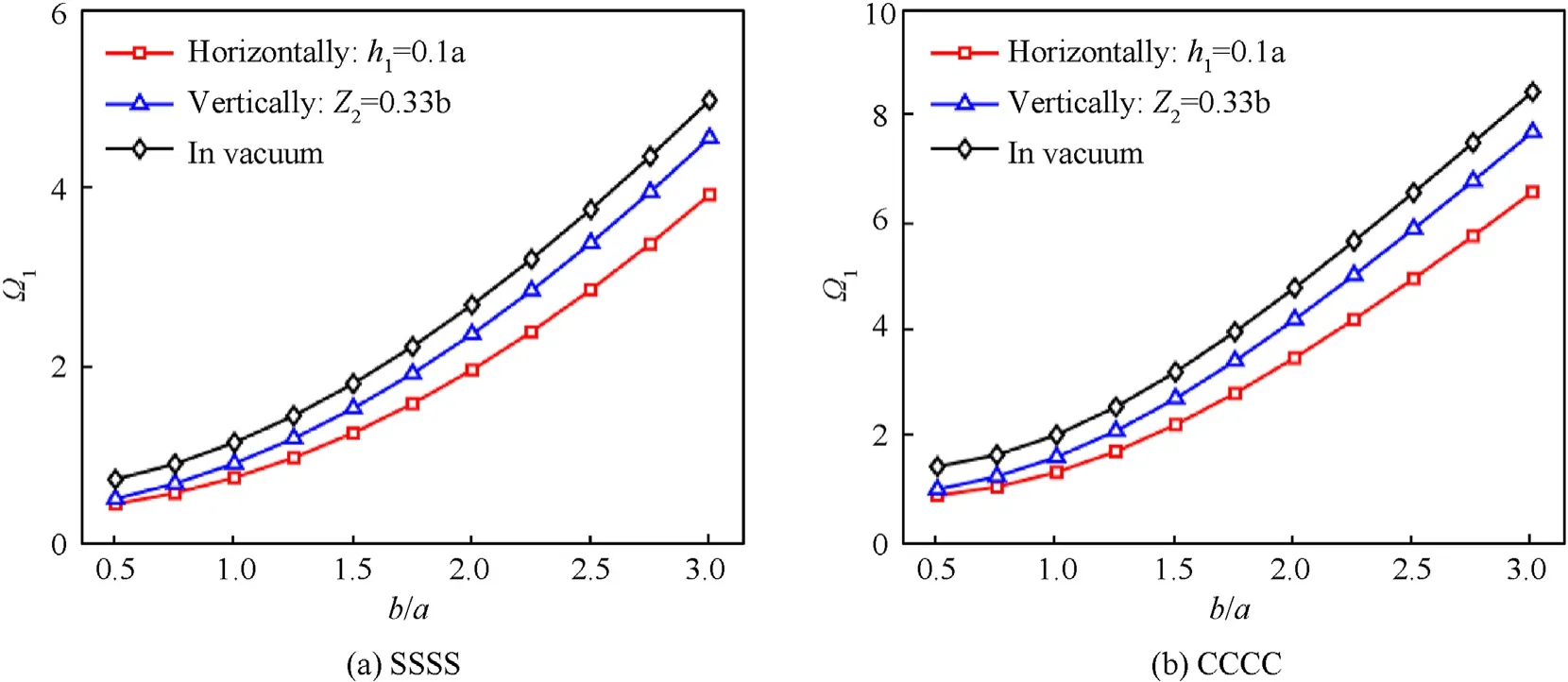
Fig.9.Effects of the width-to-length ratio b/a on the dimensionless natural frequency Ω1of the Al/Al2O3 BDFG plate(a=1,h/a=0.1,d2=d1)with different boundary conditions:a) SSSS;b) CCCC.

Finally,the influence of the fluid density ρon the natural frequency Ωis plotted in Fig.13.As observed from figure,the greater the fluid density ρincreases,the lower the natural frequency Ωbecomes.In particular,the horizontal plate partially submerged in fluid has a very rapid reduction in natural frequency,with ρ=1200kg/mand Al/AlOthe natural frequency decrease 33.04%;and with Al/ZrOthe natural frequency decrease 35.6%.The reduction law of the natural frequency of the vertical plate is almost linear according to change of the fluid density ρ,while this law of the horizontally plate is almost nonlinear.

Fig.10.Effects of the power-law indexes px,pz on the dimensionless natural frequency Ω1of the Al/Al2O3 square BDFG plate (a=1,h/a=0.1,d2=d1) with the CSCS boundary condition.

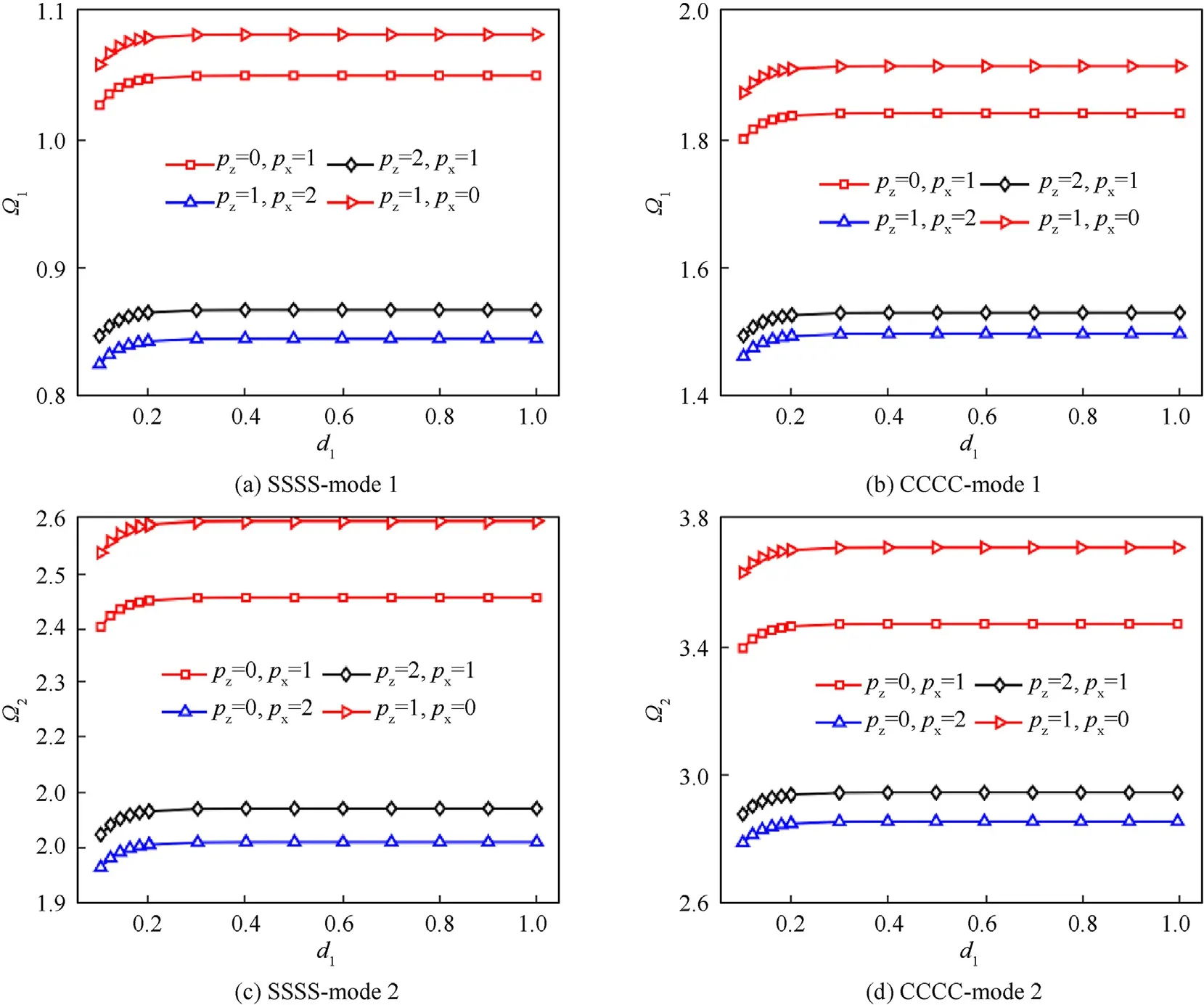
Fig.11.Effects of the submerged distance d1 in fluid on the dimensionless natural frequency Ωm of the Al/Al2O3 square BDFG plate (a=1;h/a=0.1,Z2=0.3b).

5.Conclusion

The present work presented an isogeometric analysis (IGA) for free vibration response of bi-directional functionally graded(BDFG)rectangular plates in the fluid medium.Material properties of the BDFG plate change in both the thickness and length directions via power-law distributions.The proposed method is based on Hamilton's principle and the refined quasi 3D plate theory to obtain the governing equation of motion of the BDFG plate.The horizontal and vertical BDFG plates are partially submerged or completely submerged in the fluid,which is considered homogeneous,incompressible,inviscid and has no rotation.The variations of Young's modulus,Poisson's ratio is derived by the Mori-Tanaka model and mass density is obtained by the Voigt model.The accuracy and reliability of the proposed solutions are verified by comparing the obtained results with those published in the literature.In addition,based on the numerical studies,some additional points are withdrawn as follows:

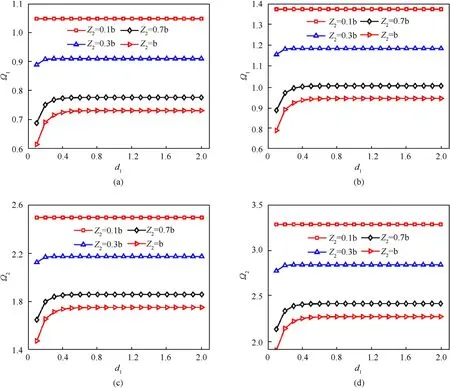
Fig.12.Effects of the submerged distance d1 in fluid on the first two dimensionless natural frequency Ωm of the Al/Al2O3 and the Al/ZrO2 square BDFG plate (with the SSSS boundary condition) partially submerged in fluid.(a=1;h/a=0.1,px=0.5, pz=2).

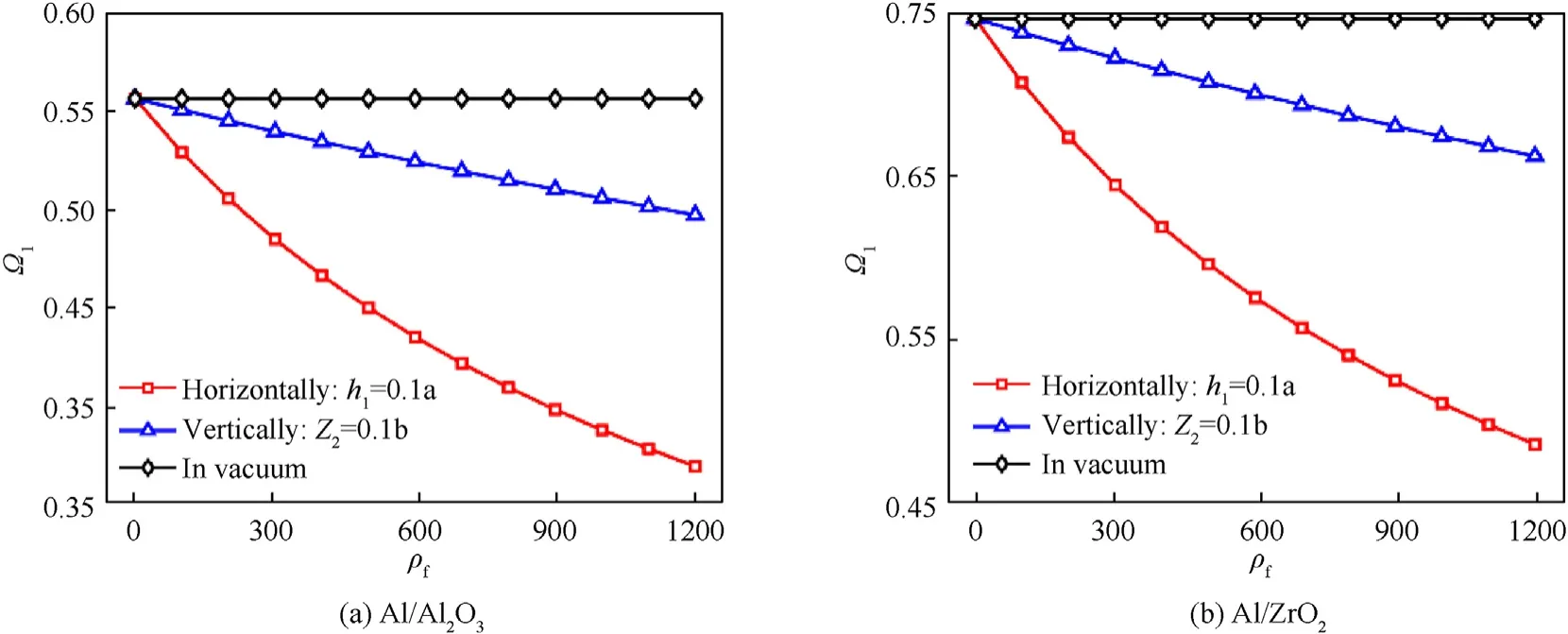
Fig.13.Effects of the fluid mass density ρfon the dimensionless natural frequency Ω1of the Al/Al2O3 and the Al/ZrO2 square BDFG plate.(a=1;h/a=0.1,px=1, pz=1,d2=d1).

· When the submerged level in the fluid of the BDFG plate Zincreases,the natural frequency Ωdecreases.However,when the submerged level in the fluid of the BDFG plate Zincreases to h=a,Z=b,the natural frequency Ωdoes not change.

· The increase of the length-to-thickness ratio (a/h)of the BDFG plates submerged in fluid leads to the increase of the natural frequency Ωto a maximum value,and then to a decrease.While the increase of the length-to-thickness ratio (a/h)of the BDFG plate in a vacuum only leads to the increase of the natural frequency Ω.

· The increase of the width-to-length ratio b/aof the BDFG plates submerged in fluid gives the changing law of the natural frequency Ωsimilar to the changing law of the BDFG plate in a vacuum.

· The increase of the power-law indexes p,por the increase of fluid mass density ρmakes the natural frequency Ωdecrease.For the BDFG plate partially submerged in fluid,the increase of the submerged distance dleads to the increase of the natural frequency Ω,however,it only increases to a certain value and then is almost unchanged.

The data used to support the findings of this study are included in the article.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under Grant number 107.02-2019.330.