多途径搭建平台,发展空间观念
——“由三视图描述几何体”的教学及其思考
2022-08-29樊贞慧浙江省宁波市第七中学
樊贞慧(浙江省宁波市第七中学)
空间观念是《义务教育数学课程标准(2022 年版)》(以下简称《标准》)提到的核心素养的主要表现之一。空间观念的内涵包含了“根据几何图形想象出所描述的实际物体;想象并表达物体的空间方位和相互之间的位置关系”,《标准》不仅将发展空间观念作为核心概念和目标,同时也在三个学段都重视了发展学生空间观念的内容设置。长久以来,传统的教学方式往往停留在机械式地呈现立体图形,缺少合理的组织方式,使“发展学生的空间观念”流于形式。如何有效利用教材内容发展学生的空间观念?笔者认为应当合理运用现实情境和学生经验,利用多种途径搭建平台。下面以浙教版《义务教育教科书·数学》九年级下册(以下统称“教材”)“3.3 由三视图描述几何体”一课的教学为例,具体阐述对“空间观念”的教学过程与思考。
一、教材分析
教材在第3章“投影与三视图”中安排了4节课内容来学习。本节课是在学生已有投影、画简单几何体的三视图的基础上,反过来从三视图想象几何体或实物模型。由于空间图形是三维的,而平面图形是二维的,从二维图形向三维图形转换,对学生的空间想象力和推理能力有较高的要求。因此,本节课既要借助直观使学生对抽象图形有形象的感受,又要进一步培养学生的空间想象力,为学生学习高中立体几何打下基础。本节课具有承前启后的重要作用,也是发展学生空间观念的重要载体。本节课的教学目标是:学会根据三视图描述出简单几何体的形状或实物原型;经历探索简单几何体的三视图还原为几何体的过程,进一步发展空间想象力;让学生学会关注生活中有关的数学问题,提高数学应用意识,在探索中养成严谨思维的习惯,获得成功的体验。
二、教学过程设计
1. 创设情境,提出问题
上课伊始,笔者利用多媒体演示如下问题:如图1,你能根据以下信息制作这个几何体模型吗?长方体的长为20 cm,宽为10 cm,高为10 cm;圆柱底面半径为5 cm,高为10 cm。
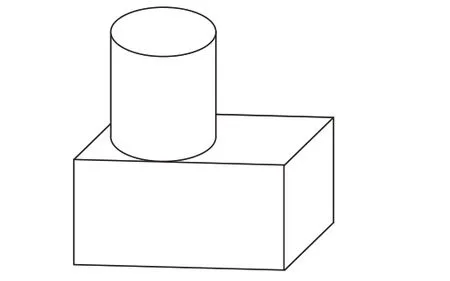
图1
【设计意图】创设情境的主要目的是体现由三视图描述几何体的必要性。在教学片断中创设了这样的情境:给出一个由圆柱体和长方体组合而成的几何体,虽然给出了圆柱体和长方体的数据,但是由于未明确给出圆柱体在长方体上的确切位置,使得学生发现这些信息不足以描述该几何体,从而引发学生思考:是否有更好的方法描述这个几何体?
接着,笔者介绍在实际生活中家具、汽车的建造往往从三视图开始设计,体现三视图描述的广泛性和实用性,再次提出问题:如何根据三视图想象几何体?
【设计意图】提出问题“能否确切描述几何体”,让学生初步感受三视图描述几何体的优越性,再通过三视图在实际生活中的广泛应用,启发学生思考如何利用三视图描述几何体,激发学生的学习兴趣和强烈的求知欲望。
2. 合作学习,探索规律
笔者出示教材中的“合作学习”,让学生在独立思考的基础上进行合作交流,然后由小组学生代表进行个别回答,笔者追问:你是如何推断的?帮助学生逐步体会从三视图推断几何体的方法。
这里,对每组三视图采用的策略是:学生描述推断过程—电脑验证—共同归纳方法。最后,学生谈体会,从中归纳出由三视图描述几何体的一般方法:视图想象、综合定形和确定尺寸位置。
【设计意图】学生通过独立思考,再进行合作探究,往往会形成学生自己的个人经验。在这个环节中,教师通过追问学生如何推断来暴露学生的思考过程,进而固化为经验,再上升到方法,从感性认识上升到理性认识,符合学生的心理特点,也体现了学生的实际认知过程。
为了巩固学生体会的经验和获得的方法,教师设计练习:如图2,根据两组三视图推断几何体。
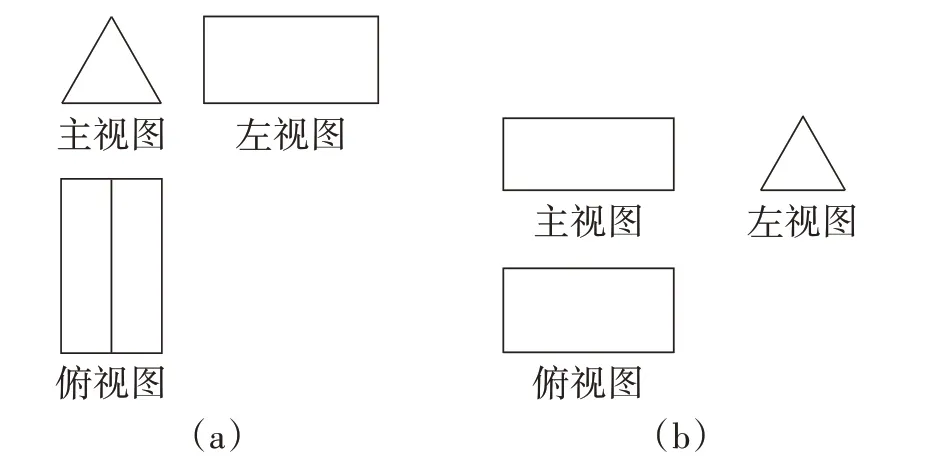
图2
【设计意图】虽然给出两组不同的三视图,但是认真思考可以发现两组三视图描述的是同样的几何体——直三棱柱,使学生感受“不同的三视图,可能表达的是同一几何体的不同摆放方式”。通过练习,学生进一步熟悉了由三视图推断几何体的方法,同时也为后续练习做了较好的铺垫。
3. 视图计算,体现应用
学生利用已有经验,根据如图3所示的三视图,推断其表示的几何体,再结合相关数据计算侧面积,同时归纳出计算直棱柱侧面积的方法,即底面周长×高。
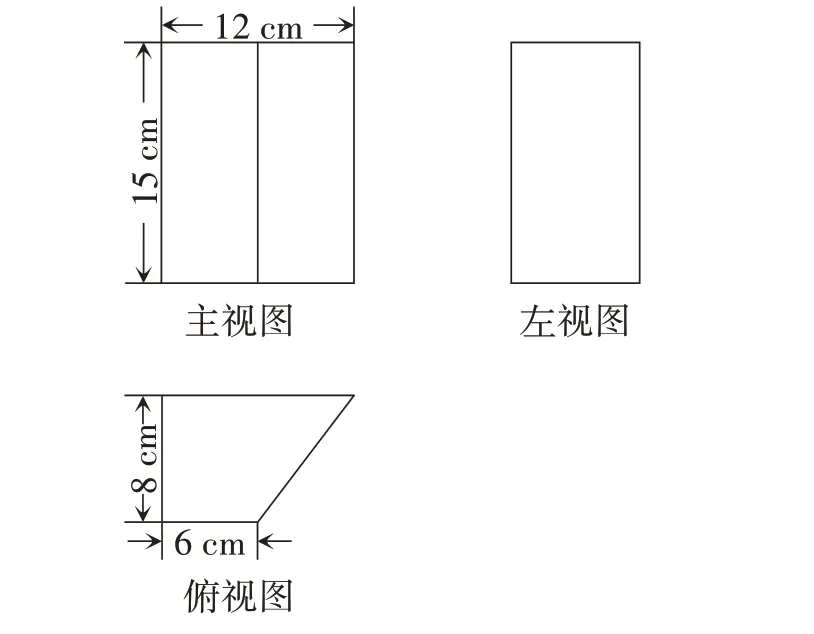
图3
【设计意图】给出视图尺寸,将三视图与物体更紧密地联系起来,进一步巩固了由三视图推断几何体的方法,体现了三视图描述几何体的特点。
接着,笔者给出如下配套练习。
练习1:如图4,推断三视图表示的几何体,并计算侧面积。
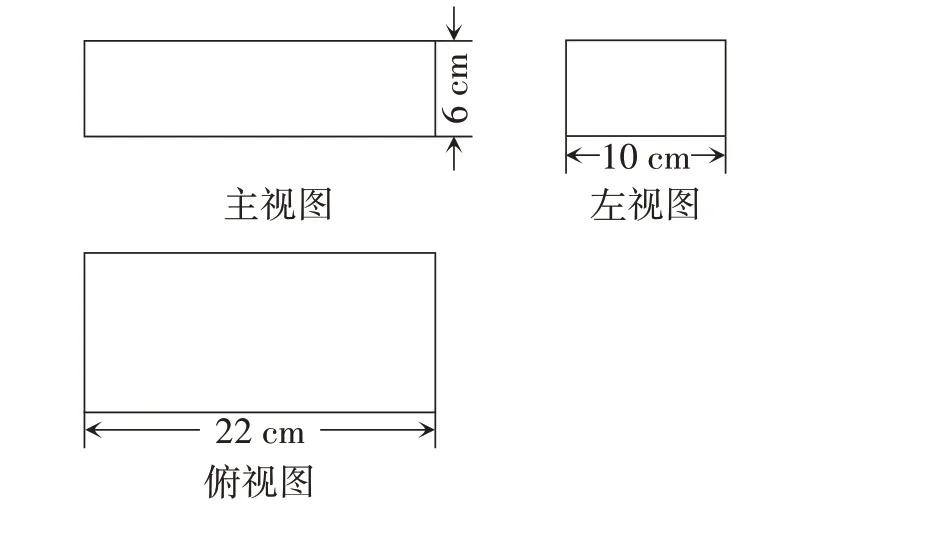
图4
练习2:用相同大小的小立方块搭几何体,它的主视图和俯视图如图5 所示,这样的几何体需要几块小立方体?

图5
练习3:用6个相同的小立方块搭几何体,它的俯视图如图6所示,能搭多少种不同的几何体?
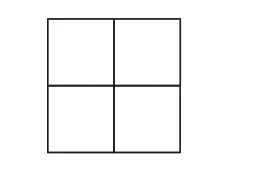
图6
【设计意图】三个练习依次递进。练习1 给出了三个视图,推断几何体并计算侧面积,需要学生对范例进行模仿;练习2 给出两个视图,推断几何体,学生发现几何体有多种情况;练习3 给出一个视图,并通过同一个几何体的不同放置方式与上述内容联系起来。三个练习从“三视图—二视图—一视图”,难度逐步提高,挑战学生思维。
4. 寓教于乐,拓宽视野
笔者给出如下游戏:有一个人,收藏了三只形状各异的瓶子,它们的瓶口形状分别如图7 ~9 所示。现在他想做一只瓶塞,对三个瓶子都适用,能做到吗?发挥你的想象力,用橡皮泥尝试设计。
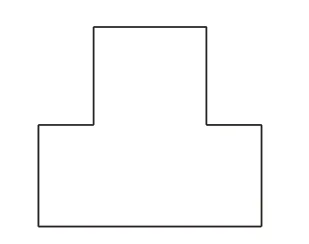
图7

图8

图9
【设计意图】不仅在生活中可以由三视图描述几何体,利用三视图也能设计游戏。在练习中,主要以规则形状描述几何体。为了激发学生的深度思考,本环节设计为游戏形式,加大图形的复杂程度,利用橡皮泥,让学生在动手、动脑中锻炼其动手能力和空间想象力。
接着,笔者介绍数学史上著名的“牟合方盖”,拓宽学生的视野。你能想象出三个视图分别是两个半径相等的圆和一个正方形的几何体吗?“牟合方盖”就是这样的几何体,并利用“牟合方盖”找到了球体体积的计算方法。
【设计意图】本环节中通过对“牟合方盖”的欣赏,介绍我国古代数学家的成就,体现了三视图的广泛应用,潜移默化地传播了数学文化。
5. 总结归纳,反思课堂
根据三视图描述简单的几何体,你有哪些方法或经验?帮助学生整理方法。
【设计意图】本环节的梳理由三视图描述几何体的方法和经验,学生在思考整理中进一步体会推断几何体的方法和经验,并在相互交流分享中共同提高。
三、教学反思
本节课从“为什么要利用三视图描述几何体?如何利用三视图描述几何体?利用三视图描述几何体有哪些应用?”三个方面循序渐进地整体架构教学,体现了几何对象的研究规律,遵循了学生学习新知识的特点,注重发展学生的空间观念,主要体现在以下三个方面。
1. 合理运用现实情境和学生经验,发展空间观念
空间观念的形成基于对事物的观察和想象,而现实世界中的物体及其关系是学生观察的最好材料,学生的已有经验也是观察、想象、分析的基础。在教学中,笔者给出学生熟悉的实物模型,让学生感受使用三视图描述几何体的必要性,又通过现实生活中的汽车、家具等实物展示,通过观察让学生从现实模型感悟如何描述几何体。
2. 搭建操作、思考和想象的平台,发展空间观念
发展学生的空间观念有多种途径,如生活经验的回忆与再现、实物观察与描述、摆拼与画图、折纸与展开、分析与推理,在教学中关键是恰当地安排学生的活动,让学生在活动中获得切身的体验。通过三个层级递进的练习,从三视图到二视图再到一视图,学生通过画图、思考和想象,感悟三视图与几何体之间的关系,培养了学生的空间想象力。
3. 及时梳理、归纳经验强化认知,发展空间观念
学生空间观念的培养不是一蹴而就的,它需要经验的不断积累和认知的不断强化。在本节课教学中,教材提供了三组根据三视图想象几何体的素材,学生通过合作学习说出结果时,笔者及时追问怎么想的,通过学生思维过程的暴露不断总结出有序思考的经验:视图想象、综合定形和确定尺寸位置。在练习中,使学生感受“不同的三视图,可能表达的是同一几何体的不同摆放方式”。这些经验有助于学生更好地认识几何体,强化对图形的位置关系和数量关系的认识,从而发展空间观念。
