基于POD -RBF代理模型的迭代更新反演方法
2022-08-29吕小龙姜冬菊
吕小龙, 黄 丹,姜冬菊
(河海大学 力学与材料学院,南京 211100)
1 引 言
水工大坝等大体积混凝土工程结构的材料参数对其健康和安全状态的监测起着十分重要的作用,但结构内部的材料参数往往难以直接得到,于是通过位移等可观测量来反演坝体材料参数便成为一种广泛使用的途径。然而,现有的大量大体积结构材料参数反演方法往往需要通过有限元等数值方法进行大规模正分析,且正分析耗时量随着待反演参数的增加呈几何式增长。对于复杂的大体积结构,甚至可能导致较多参数反演问题的正分析环节难以施行。通过建立代理模型以取代大量的有限元计算,可以花费很少的时间获得足够精度的响应值,因而广泛应用于结构优化、可行性分析和预测反演等问题中[1]。
Bhosekar等[2]对各种常见代理模型的构建、应用及优势进行了总结。代理模型本质上是输入和输出之间的一种映射关系,常见的映射模型包括多项式模型[3]、Kriging插值模型[4,5]、径向基函数模型[6-8]以及人工神经网络模型[9,10]等。其中采用本征正交分解POD(Proper Orthogonal Decomposition)和径向基函数RBF(Radial Basis Functions)插值相结合构建的代理模型,能同时保证较高的拟合精度和插值精度[11],适用于大体积结构的模拟预测。本文研究思路即来自于此。此外,为了在保证反演精度的前提下尽可能降低有限元正分析计算量,本文结合粒子群算法的全局寻优能力和高斯-牛顿法的局部快速收敛能力,构建了一种组合式的迭代更新反演模型,并通过典型大体积混凝土大坝的分区弹性模量反演验证其反演精度和计算效率。
2 代理模型构造及原理
2.1 本征正交分解(POD)
POD是统计学上用来分析数据的常用方法[12],在数据科学领域也称为主成分分析。以典型水工大坝为例,考虑将大坝分成p个弹模分区,设置n组弹模样本得到弹模参数样本矩阵X=[x1,x2,…,xn],其中xi(i=1,2,…,n)为包含一组弹模值的列向量。在相同荷载作用下,其分区弹模不同的取值对应不同的位移响应,设位移响应矩阵为Y=[y1,y2,…,yn],其中yi(i=1,2,…,n)为m维位移响应列向量,表示在一组分区弹模值下大坝上m个测点的位移测值所组成的列向量,称之为快照(Snapshot),n为样本数量。POD的关键目的就是找出这些快照的内在联系,提取数据的主要特征,进而对数据进行降维。对Y进行奇异值分解
Y=Φ·Λ·VT
(1)
式中Φ=[φ1,φ2,…,φm] (φi⊂Rm,i=1,2,…,m)为Y的左奇异向量,V=[v1,v2,…,vn] (vi⊂Rn,i=1,2,…,n)为Y的右奇异向量,Λ为m行n列的对角矩阵,其对角线上的每个元素λi(i=1,2,…,min(m,n))为Y的奇异值,即协方差矩阵YTY的特征值的平方根。对大部分情况,奇异值λi(i=1,2,…,min(m,n))从大到小衰减的速度很快,前几个奇异值的总和通常就能占到所有奇异值总和的90%以上,即
(2)
根据奇异值分解的性质,原数据Y在左奇异向量φi(i=1,2,…,n)上的投影是最大的,因此,以前k阶左奇异向量为基向量便能够包含Y的绝大部分信息。由于k通常远小于n,故原数据在保留绝大部分信息的前提下得到了大幅降维。以前k阶左奇异向量为基向量,任意弹模参数样本x对应的位移响应向量y(x)可以近似表示其线性组合为

(3)

2.2 径向基函数(RBF)模型
RBF是一种常用的多变量函数插值基函数,其一般形式可记为
(4)

Thin-platesplines函数:
f(r)=r2lnr
(5)
Inverse multiquadric函数:
f(r)=(r2+c2)-1/2
(6)
以及高斯函数:
f(r)=exp(-r2/c2)
(7)
式(6,7)的c为一个大于零的常数,称为平滑系数,其值越大,函数值变化越平缓,反之越陡峭。综合已有工作比较,本文采用inverse multiquadric函数作为径向基函数,平滑系数c=0.5。
将所有已知样本参数点和对应的位移响应代入插值式(4)中,并写成矩阵形式
(8)

2.3 形成POD -RBF代理模型
根据RBF插值方法,可对方程(3)的组合系数α(x)进行插值,即
(9)
或矩阵形式
α(x)=W·f(r)
(10)
式中W为wi j组成的系数矩阵,f(r)为f(ri)组成的列向量。将式(10)代入式(3),并应用已有的所有样本点得到

(11)

(12)
即可求得系数矩阵W。
由式(3,10,12)可得POD -RBF代理模型
(13)
3 迭代更新反演算法
参数反演精度在一定程度上依赖于代理模型的精度,但在全局上构建高精度的代理模型,需要通过大量的有限元正分析获取足够多的样本点,这往往需要极大的计算消耗。若只在待反演参数点的附近布置较密的样本点,而在其他地方稀疏取样,使得代理模型仅在局部具有相对高的精度,便能够通过较少的样本点获得尽可能高的反演精度。
粒子群算法PSO(Particle Swarm Optimization)是一种基于群体的随机优化算法[13,14],具有较好的全局寻优能力,但因为其随机性,在局部的收敛速度较慢。基于梯度信息的高斯-牛顿法虽然容易陷入局部极小,对初值的选取要求较高,但其在局部区域往往比粒子群等启发式算法具有更快的收敛速度以及求解精度。因此将两者结合起来,便能够在一定程度上同时保证全局最优性、局部精度和收敛效率。
对于大多数参数反演问题,待反演参数总是落在参数空间的局部区域,而在全域构建高精度的代理模型则需要消耗大量的计算机时。为此本节构建了一种基于代理模型的迭代更新反演算法,能够在提高反演效率的同时获得更高的精度。
迭代更新反演的步骤如下。
(1) 在全域稀疏采样以尽可能广地覆盖参数空间,通过有限元等数值方法获得相应的位移响应,得到初始样本集S0。
(2) 根据样本集S0建立代理模型。此时的代理模型虽然精度不高但能反映总体特征。
(3) 基于PSO算法的全局寻优能力找到一个极值点x0作为反演结果。由于代理模型的精度较低,反演出的结果通常和真实值也有较大的差距。
(4) 计算反演参数下的位移响应,迭代更新。若计算出的位移与实测位移差距较大,则将此反演参数和有限元计算的位移响应作为新的样本对加入到初始样本集S0中,得到新的样本集S1。
(5) 使用增加样本点后的样本集S1重新构建代理模型。此模型将具有在x0附近更高的精度。由于已通过PSO算法找到全局最优的局部区域,此时可以改用局部收敛速度更快的高斯-牛顿法继续反演,这样能够在提高反演速度和精度的同时避免PSO算法每次都进行全局搜索带来的不稳定性。
基于POD -RBF代理模型结合PSO算法和高斯-牛顿法的迭代更新反演算法具体流程如图1所示。
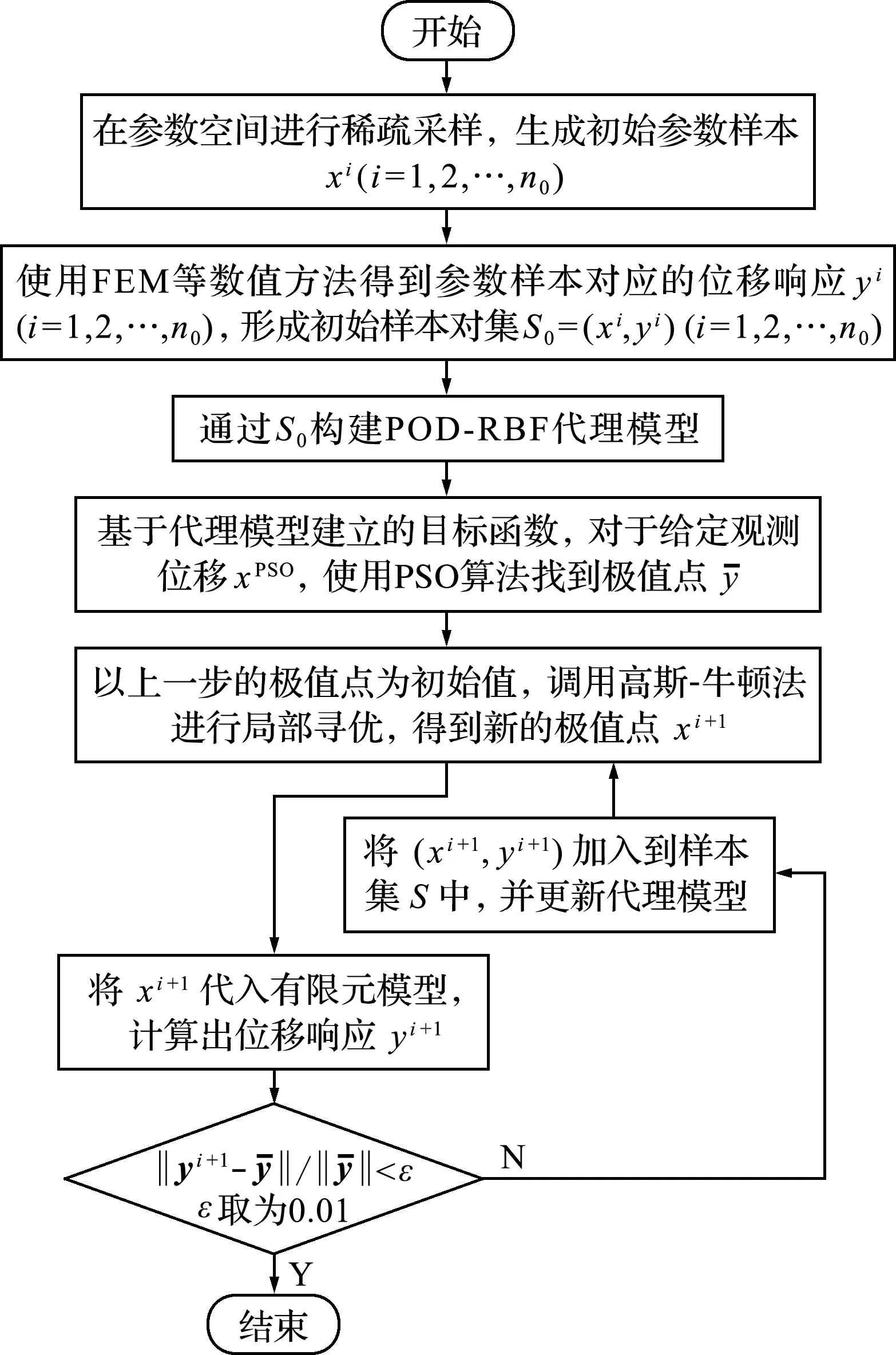
图1 迭代更新反演算法流程
4 算例分析
4.1 模型概况
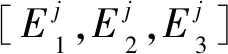

图2 混凝土大坝有限元模型
4.2 有限元代理模型
代理模型的精度一定程度上取决于样本数量,充足的样本集有利于构造高精度的代理模型,但相应地也会消耗更多机时。因此,选取合适的样本数量以更经济的方式构建代理模型是十分重要的。
本节分别选取了不同数量的样本集来构建代理模型,并统计了代理模型对测试样本的计算位移和对应的有限元计算位移之间的平均相对误差,结果如图3所示。可以看出,针对本算例的有限元模型,当选取样本数量小于9时,样本数量的增加对代理模型精度的提升作用明显,而当样本数量大于9之后,样本数量的进一步增加并不能再显著提升代理模型的精度。因此本算例选取9个样本作为初始样本集。

图3 不同样本个数下POD -RBF模型的平均相对误差
在对位移响应矩阵进行奇异值分解时,其前几阶奇异向量包含了绝大多数特征信息,通常只需提取前几阶就足以获得较高精度。在本算例中,对9个样本组成的位移矩阵进行分解,得到其前五个奇异值列入表1。

表1 位移响应矩阵奇异值
由表1可知,位移矩阵前3阶奇异值占总奇异值比重已达95%以上。截取不同个数奇异向量作为基向量进行插值引起的平均相对误差如 图4 所示。代理模型的平均相对误差的变化趋势与奇异值的变化趋势相反,这表明随着奇异值占比的增加,模型精度相应提高,当使用前3阶奇异向量构建代理模型时,代理模型相对误差已降至接近最低水平。
4.3 迭代更新反演结果
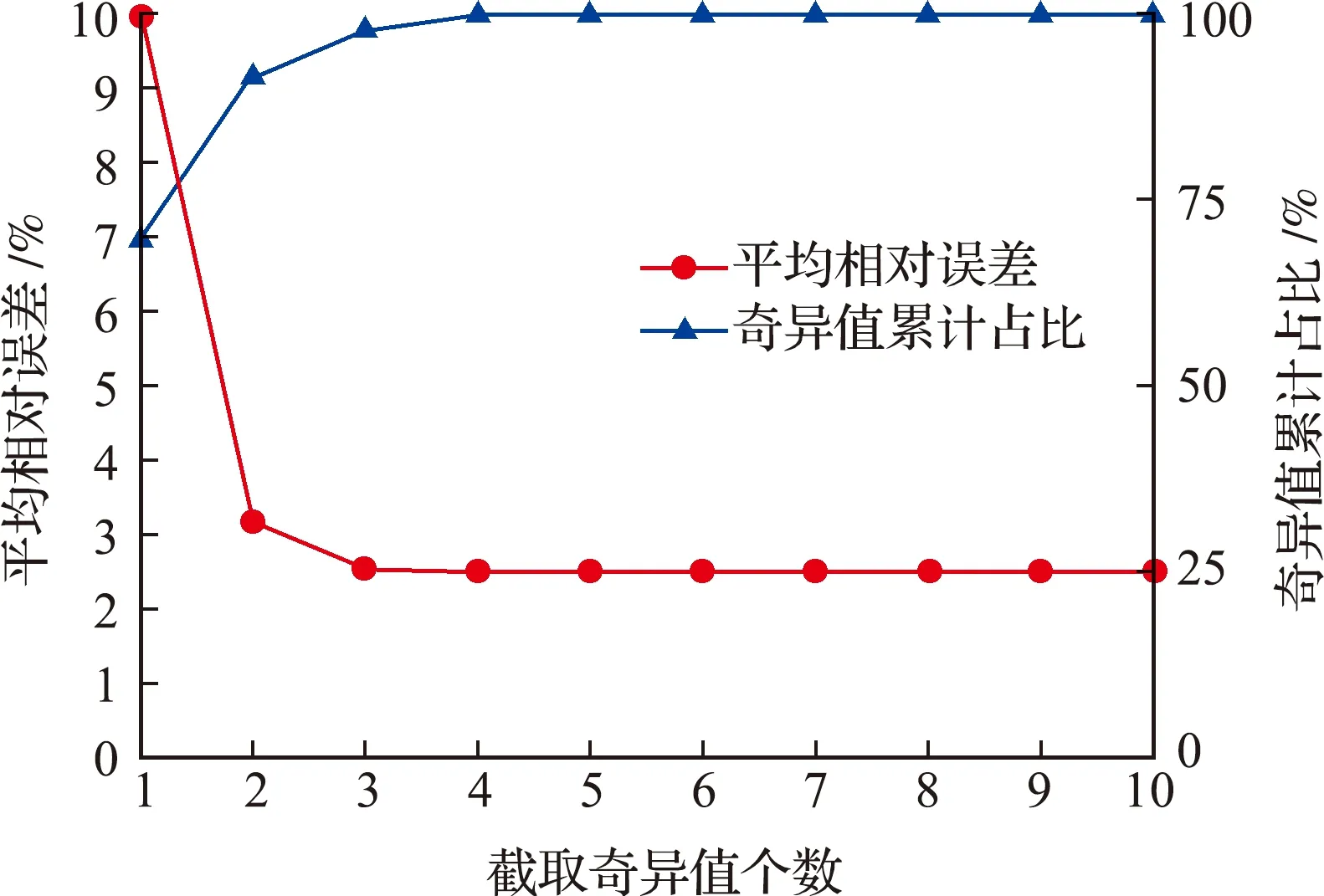
图4 平均相对误差和奇异值占比随截取奇异值个数的变化
为验证本文反演方法的高效性,将文献[15]的基于BP神经网络的直接反演方法加入进行对比。本文BP神经网络的隐含层神经元个数取为10,激活函数为Sigmoid函数。两种方法的反演结果列入表3,由表3可知,与BP直接反演方法相比,基于POD -RBF代理模型的迭代更新反演方法在反演精度和稳定性上表现都要更优。

表2 迭代更新与无迭代更新反演结果对比

表3 迭代更新反演与BP直接反演结果对比
5 结 论
本文针对大型复杂结构参数反演时通常耗费大量正分析机时的问题,尝试构建本征正交分解(POD)结合径向基函数(RBF)的代理模型,并结合粒子群算法(PSO)的全局寻优能力和高斯-牛顿法(GNM)的快速局部收敛特性,开展兼具精度和效率的迭代更新反演算法探索,并应用于典型混凝土重力坝坝段的分区弹性模量反演。
通过比较不同样本数量下代理模型的精度,在确保代理模型准确性的基础上可选取合适的样本数量,有效降低代理模型的计算机时消耗。
典型算例分析表明,基于本文方法,可先使用相对较少的样本数量构建相对粗糙的代理模型,然后在反演过程中不断在全局最优点附近加入新样本更新代理模型,有针对性地提高代理模型的局部精度。通过结合粒子群算法的全局寻优能力和高斯-牛顿法局部快速收敛能力,可用相对较少的迭代步获得足够高的反演精度。
