梁式结构受移动荷载作用非平稳随机振动的DQ -PEM方法
2022-08-29杜永峰朱前坤
张 琼,杜永峰,朱前坤
(1.兰州理工大学 防震减灾研究所,兰州 730050;2.兰州理工大学 甘肃省减震隔震国际合作研究基地,兰州 730050)
1 引 言
梁式结构受移动荷载作用的振动问题具有广泛的工程背景,如车辆在桥梁上行驶、行人在人行桥上行走以及栈道类运输系统等均可归结为此类问题[1-5]。由于荷载作用位置变化等相关因素的影响,移动荷载一般具有随机性,梁式结构受移动荷载作用的振动一般也为随机振动[6-8]。
利用传统随机振动方法处理梁式结构受移动荷载作用时的随机振动通常需要大量的计算工作,效率较低。针对这一问题,林家浩等[9]提出了高效精确的虚拟激励法,该方法在处理非平衡随机振动问题时最大的特点是将其转化为确定性时间历程分析,计算效率提高2~4个数量级。利用虚拟激励法处理非平衡随机振动的关键是计算结构在确定性荷载作用下的虚拟响应,现有做法一般是建立有限元模型后再利用振型叠加法计算[7,8]。吕峰等[6]综合利用虚拟激励法和精细积分法提出了一种基于有限元的精确高效算法来研究桥梁的随机动力特性。赵岩等[7]基于虚拟激励法和傅里叶分析,提出了一种求解移动随机载荷作用结构非平稳随机振动的有效频域法。Caprani[10]基于虚拟激励法研究了行人通过人行桥时的随机振动情况。以上研究在计算结构确定性荷载作用下的虚拟响应时利用了振型叠加的思想,均需事先假定振型,而对于半刚性边界的梁式结构,估算精确的振型较为困难;在振型叠加过程中通常只考虑有限低阶振型的贡献,舍弃了高阶振型的影响;对于移动荷载的处理,以上做法要么通过有限元形函数向量将移动载荷向有限元节点施加,要么采用精细积分的递推格式,也较为繁琐。
可用分布参数体系的Euler-Bernoulli模型描述梁式结构,其受移动荷载作用的控制方程是含Dirac函数的偏微分方程[3,11]。Eftekhari[12,13]提出综合利用微分求积法和积分求积法结合的方法研究结构受移动荷载作用的受迫振动问题,该方法利用积分求积法离散Dirac函数,利用微分求积法离散偏微分方程,不必事先假定振型且能考虑高阶振型的影响,数值计算结果显示出较高的精度与效率。文献[4,14]将该方法推广到人行荷载作用下人行桥振动响应的求解,并与传统的振型叠加计算结果对比,证明该方法的高效性,而后又将该方法扩展到半刚性边界下的人行桥受行人荷载作用的振动响应问题[5]。
基于上述研究,本文提出将微分求积-虚拟激励方法DQ -PEM用于梁式结构受移动荷载作用的非平衡随机振动问题。利用DQ -IQ法将梁式结构受移动荷载作用下含Dirac函数的偏微分方程转化为不含Dirac函数的常微分方程,用DQ法直接将其与时间无关的微分项转化为代数项,用IQ法将表示荷载位置变化的Dirac函数转化为代数项。将表示荷载位置变化的Dirac函数视为移动荷载的非平稳化函数,再结合虚拟激励法的思想,可得梁式结构的非平稳随机响应。结合具体算例分析了半刚性梁式结构受移动荷载作用的随机振动问题,讨论了不同速度和不同边界条件等因素对梁式结构随机振动的影响。
2 梁式结构受移动荷载作用的振动方程
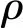
2.1 受移动荷载作用梁的振动基本方程
梁式结构受匀速移动荷载作用的振动控制方程为[3,4]
δ(x-vt)F(t)
(1)
式中u(x,t)为梁的位移,v为荷载移动速度,δ(x-vt)为Dirac函数。
引入如下无量纲量,
(2)
则式(1)变换为
λδ(X-XF(t))
(3)
2.2 边界条件

则梁式结构半刚性边界,在X=0处为
(4)
在X=1处为
(5)
2.3 基本方程的离散化
令XF=vt=Xp(1≤p≤n),利用DQ -IQ混合法以及Dirac函数的性质[4,12,13],式(3)转化为
(6)
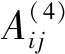
微分求积1阶权系数可显式计算[15]为
(7)
高阶权系数则由递推公式计算为
(8)
四阶微分方程每个端点有两个边界条件,X节点选取采用如下形式[15],
(9)
式中 Δ为相邻两边节点的距离,Δ可在10-2和10-4之间取值。
积分求积权系数Ri为[12]
(10)
式中 ΔXi=Xi + 1-Xi。
式(6)写成矩阵形式[14]为
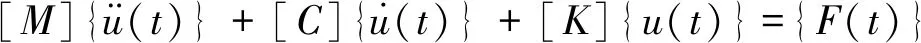
(11)
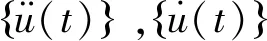
[M]=α[I], [C]=β[I], [K]=[A](4)
(12)
式中 [A](4)为微分求积4阶加权系数矩阵[A],I为n×n的单位矩阵。
根据荷载在网格点上的静力平衡,可得到荷载模型[12,14]
(13)
式中XR=Xp-XF(t),XL=XF(t)-Xp - 1。
2.4 边界条件的离散化
边界条件式(4,5)的DQ格式为[4]
u(0,t)=0,
(14a,14b)
u(1,t)=0,
(14c,14d)
式(14a,14c)代入式(14b,14d)后联立求解二元一次方程组得
(15a)
(15b)

(16a)

(16b)

(16c)

(16d)
2.5 振动控制方程的离散化及求解
把式(14a,14c,15)代入式(11)得
(i=3,4,…,n-2)(17)
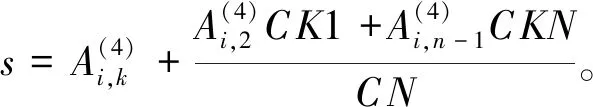
式(17)为二阶常系数微分方程,利用Newmark或精细积分算法即可得到数值解。
由式(17)退化可得到梁式结构梁频率特征方程为
s{u}=Ω2{u}
(18)
式中Ω为梁式结构的圆频率,{u}={u3,u4,…,un - 2}。
3 梁式结构受移动荷载作用非平稳随机振动的DQ -PEM法
虚拟激励法是在桥梁抗震分析中发展出来的随机振动系列算法,该方法在处理非平衡随机振动问题时最大的特点是将其转化为确定性时间历程分析。尽管式(1)中荷载F(t)是一个平稳过程,但由于作用位置不断变化,加之梁式结构为有限长度,因此对梁式结构而言,外激励为非平稳随机过程。式(1)右边的荷载项亦可视为由Dirac函数与荷载F(t)组成的外激励均匀调制模型:
x(t)=δ(x-vt)F(t)
(19)
F(t)为平稳随机过程,假设荷载F(t)的自谱密度为SX X(ω),构造虚拟的移动确定性外部激励 ,可写为
(20)
替换式(1)右边的荷载项,则虚拟响应为
(21)
I(ω,t)为给定的确定性激励δ(x-vt)exp(iωt)下结构的响应,可由DQ -IQ混合法求得。
由结构的虚拟响应,进一步可得到结构响应的演变谱密度为
SX X(ω)I*(ω,t)IT(ω,t)
(22)
4 非平稳随机振动的DQ -PEM法计算步骤
梁式结构受移动荷载作用非平稳随机振动的DQ -PEM法的计算步骤如下。
(2) 已知结构的输入功率谱SX X(ω),将整个外荷载的频率域ω划分成N段,间隔为Δω,离散后每段外荷载频率为ωn=nΔω。
(3) 利用DQ -IQ混合法求解每个ωn对应的确定性荷载确定性激励δ(x-vt)exp(iωnt)作用下结构的响应I(ωn,t)。
(4) 按式(22)求得每个ωn对应的响应的演变功率谱密度SU U(ωn,t)。
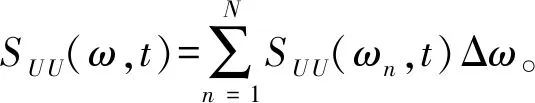
5 工程算例
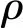
图2为运用传统的振型叠加法和DQ -PEM法下的加速度响应,蓝线是振型叠加法算出的加速度响应,红线是DQ -PEM法算出的加速度响应。可以看出,曲线几乎一致,验证了DQ -PEM法的准确性。
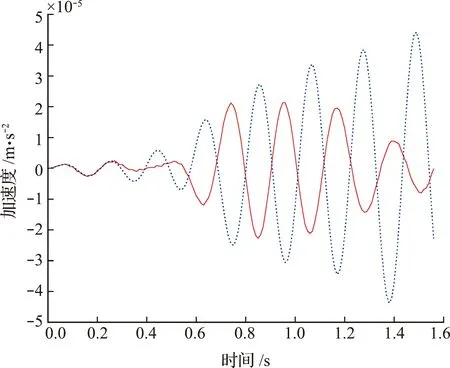
图2 加速度响应
5.1 梁式结构自振频率
5.2 速度对随机振动响应统计量的影响
图3为不同移动速度下,简支梁式结构跨中的位移演变功率谱。为了方便对比数值结果,采用荷载瞬时位置(x=Vel·t)表示x轴坐标。可以看出,梁式结构的位移响应功率谱的峰值均在其自振频率4.77 Hz附近,与荷载移动速度无关,其峰值由共振现象造成。荷载移动速度为25 km/h,50 km/h 和100 km/h时,对应的位移响应演变功率谱峰值分别为2.87×10-7,2.04×10-7和1.11×10-7m2/Hz,其中50 km/h和100 km/h对应的位移响应演变功率谱峰值为25 km/h时的0.71倍和0.39倍。可见,随着移动荷载速度的增大,荷载作用时间变短,响应演变功率谱的峰值随之减小,但其频带会相应变宽。这一现象与文献[6,7]一致。图4为荷载以不同速度通过简支梁式结构时,其跨中位移响应的时变方差。荷载移动速度为25 km/h,50 km/h和100 km/h对应的位移响应时变方差最大值分别为3.10×10-6m2,2.80×10-6m2和2.24×10-6m2,其中50 km/h和 100 km/h 对应的位移时变方差最大值为25 km/h时的0.90倍和0.72倍。可以看出,梁式结构跨中处的时变方差最大值随着荷载速度的增大而减小,最大值出现时间随着荷载速度的增大而后移。
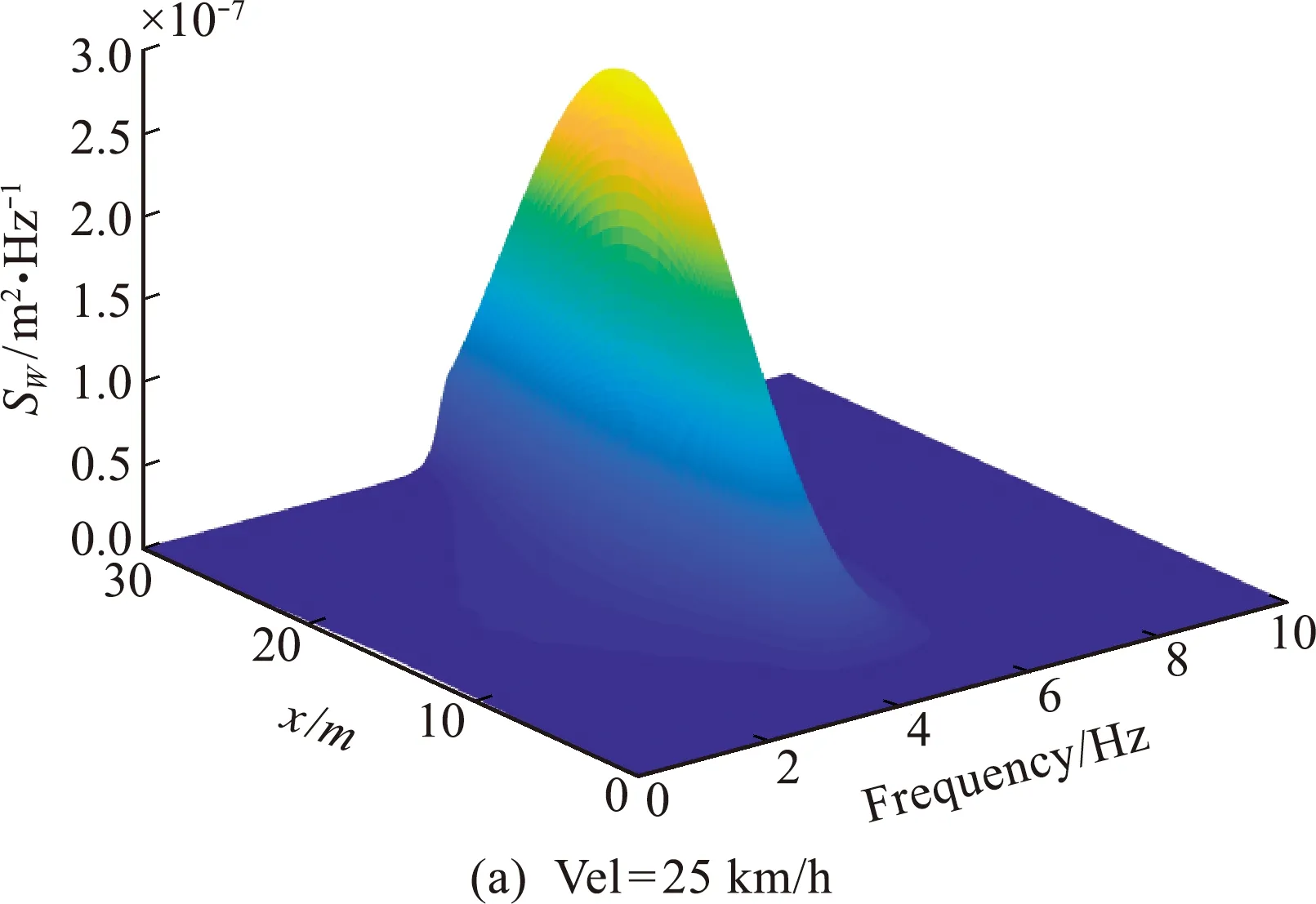
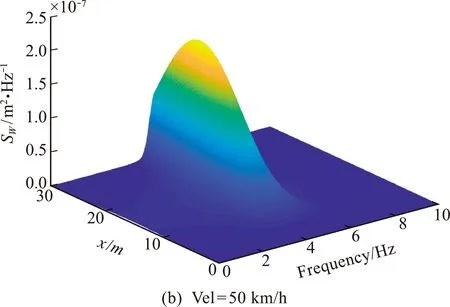
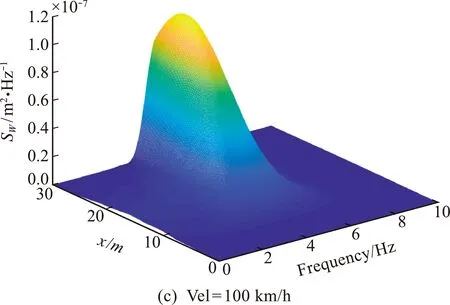
图3 不同速度下梁式结构跨中的位移响应演变功率谱
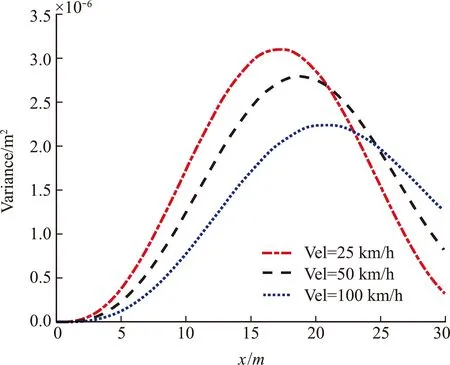
图4 不同速度下梁式结构跨中的时变方差
5.3 边界条件对随机振动的影响

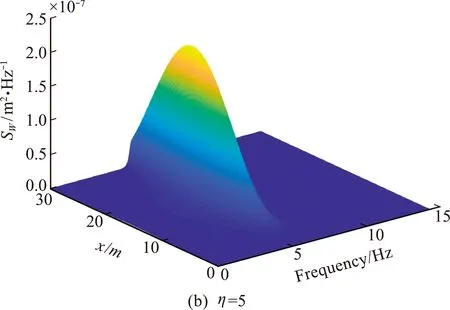

图5 不同边界下梁式结构跨中的位移响应演变功率谱

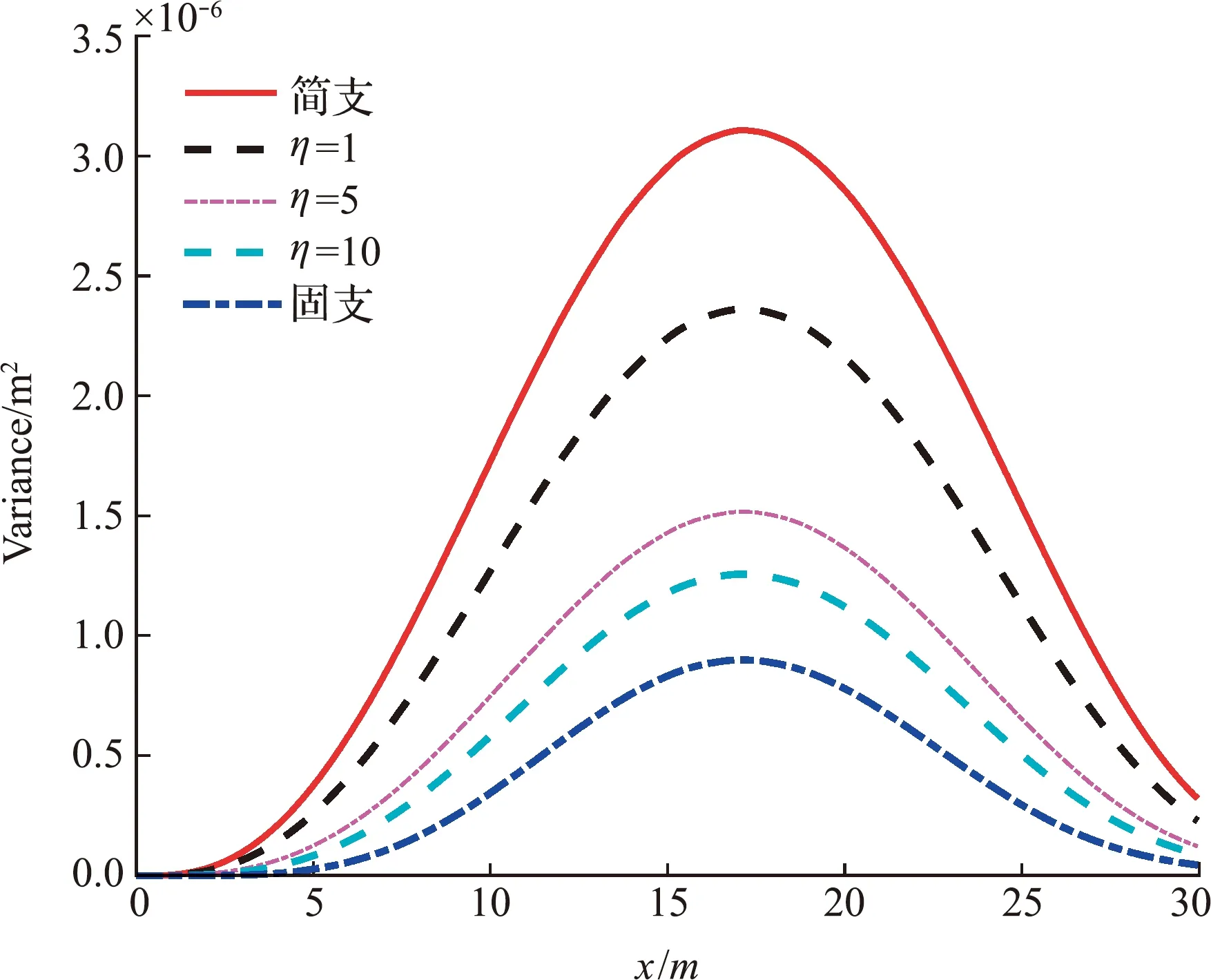
图6 不同边界下梁式结构跨中的时变方差
6 结 论
基于微分求积法和虚拟激励法,提出了一种求解移动随机载荷作用下半刚性梁式结构非平稳随机振动的高效方法。利用 DQ -IQ混合法将含Dirac函数的梁式结构受移动荷载作用的偏微分振动控制方程转化为不含Dirac函数的常微分方程。同时,将表示荷载位置变化的Dirac函数视为移动荷载的非平稳化函数,再结合虚拟激励法的思想,得到梁式结构在确定性荷载作用下的虚拟响应,进而得到其非平稳随机响应。计算结果验证了该方法的准确性与有效性;算例结果表明,当移动荷载为随机移动荷载时,响应演变功率谱的峰值出现在结构自振频率附近,且梁式结构自振频率越大,其响应的演变功率谱和时变方差的峰值越小,可通过调整半刚性系数,控制梁式结构的响应。
