基于RBFNN-FDA模型对塑料拖鞋鞋底的拉曼光谱研究

2022-08-29田陆川

上海塑料 2022年4期

田陆川，杨俊，姜红

(中国人民公安大学侦查学院，北京 100038)

0 前言

塑料拖鞋鞋底是案件现场常见物证之一，通过分析现场残留的塑料拖鞋鞋底或残渣，并与已知来源样品比对，可以推断拖鞋的产地等信息，为获取侦查线索、开拓侦查思路提供帮助。目前，法庭科学检验塑料的方法有：红外光谱法[1]、拉曼光谱法[2]、X射线荧光光谱法[3]、扫描电镜/能谱法[4]、薄层色谱法、热分析法、裂解气相色谱法等。其中，拉曼光谱法具有操作简单、灵敏度高、无需前处理等优点，因此被广泛应用于司法鉴定中。

塑料拖鞋是最常见的拖鞋种类，一般由树脂及塑料助剂(增塑剂、阻燃剂等)制成。由于不同拖鞋的用途与使用场景不同，生产厂家所选择的主要成分和填料也不尽相同，相同成分的配比也可能不同，这种差异导致了不同拖鞋对应拉曼光谱图的峰数和峰位的不同，为检验区分拖鞋鞋底种类和材质提供了依据。笔者创新性地将统计学方法应用到了拉曼数据解析中，利用主成分分析对拉曼数据降维，将提取到的3个主成分代替原有数据进行系统聚类，将收集到的43个样本分为4类，再利用径向基函数神经网络(RBFNN)与Fisher判别分析(FDA)建立基于系统聚类结果的预测模型(简称RBFNN-FDA模型)，经验证后FDA的准确率为97.7%，RBFNN的准确率为100%，效果显著。

1 实验部分

1.1 实验仪器及条件

实验仪器：FinderVista显微共聚焦激光拉曼光谱仪，北京卓立汉光仪器有限公司。

实验条件：激光光源为785 nm，激光功率为20 mW，积分时间为50 s，波数为190～2 900 cm-1，扫描次数为5，点扫描方式。

1.2 实验样本

不同来源、不同厂家的塑料拖鞋鞋底样本43个(样本表略)。

1.3 谱图采集

将样本用酒精棉签擦拭晾干，放在激光头下待测，反复调节激光头高度使光点最小;在20 mW下积分50 s，重复扫描5次，将得到的谱图进行比较，选择其中杂峰数量较少的拉曼光谱图进行保存。

1.4 实验原理

1.4.1 主成分分析

主成分分析是一种因子提取的降维方式[5-6]，通过某种正交变换从原始高维数据中提取出一个或多个与原变量线性不相关的重要变量，克服原始数据的线性相关关系。

1.4.2 系统聚类

系统聚类又称分层聚类或凝聚性层次聚类，其主要思想是将每个研究对象视为独立的一个簇，根据某种标准不断合并相似度最高的两个簇成为新簇，直到所有研究对象都被归为一个簇[7]。聚类分析要求不同组间的差异较大，个体的差异距离通常用距离来表示。笔者采用平方欧式距离进行聚类分析，其数学定义式为：

(1)

式中：dxy为平方欧式距离；xi、yi为i点的坐标;n为样点数量。

1.4.3 FDA

FDA是将未知分类的个体并入已有分类进行预测的一种多元统计分析方法[8],其分析过程为：根据已知分类的样本中的某些指标，按照一定的判别准则建立起一个或多个判别函数，利用样本的大量数据确定判别函数系数，并计算判别指标。对于一个未知分类的新样本，只需将其代入到判别函数中即可确定其分类归属。

FDA利用了投影的思想，使高维问题在一维空间中处理，通过判别函数得出变量在各个典型变量上的坐标，同时得出样本与类中心的距离，从而作为分类依据[9]。

1.4.4 RBFNN

径向基函数(RBF)是以函数逼近为基础的前反馈神经网络，相较多层感知器，RBF只有一个隐层。其主要思想是用在RBF的隐藏层内将原本的低维数据转化到高维空间中，使得原本不可分的变量在高维空间内可分[10-11]。目前最常用的RBF是高斯核函数，其公式为:

(2)

式中：k(·)为高斯核函数;ac为中心点坐标；a为待分类的坐标；σ为可调平滑程度参数。相较于BP神经网络，RBFNN的结构简单，训练简洁，学习收敛速度快，广泛应用于分类预测，系统控制等领域[12]。

2 结果与讨论

2.1 谱图解析与区分

将收集到的谱图与标准拉曼特征峰进行对照，即可得知样本所含物质。常见塑料及填料的标准拉曼特征峰见表1[13-14]。

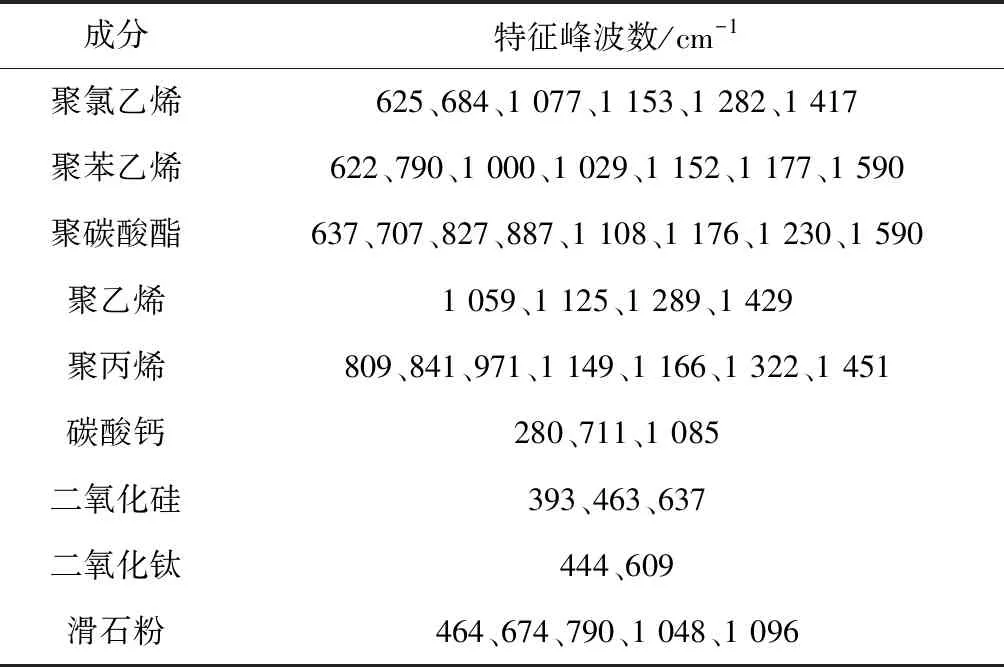
表1 常见塑料及填料的标准拉曼特征峰

随机选取6#与37#样本进行分析比较，结果见图1。由图1可以看出：6#样本有11个特征峰，37#样本有13个特征峰，样本的峰数不同；6#样本在640 cm-1、1 165 cm-1、1 290 cm-1、1 424 cm-1处有特征峰，说明6#样本主要成分为聚氯乙烯，可能含有二氧化硅；37#样本在440 cm-1、637 cm-1、1 185 cm-1、1 600 cm-1处有特征峰，说明样本主要成分为聚碳酸酯，可能含有二氧化钛。根据以上不同即可实现对样本的区分。

(a) 6#样本

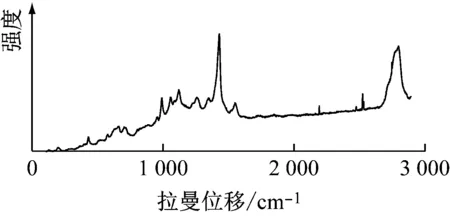
(b) 37#样本

2.2 主成分分析

拉曼数据是由拉曼位移及拉曼强度构成的高维数据，故需要对数据进行降维提取主成分替换原始数据，以消除原始高维数据间可能存在的线性关系，提高聚类分析准确度。

在提取主成分时，一般要求所提取的主成分累计方差贡献率大于85%[15]。从43个样本中提取到了3个主成分，累计方差贡献率达到了96.283%(见表2)，可以充分解释原始数据。

表2 主成分累计方差贡献率

2.3 系统聚类

系统聚类是一种无监督式的统计方法，广泛应用于数据分类与医学统计上。常用的聚类方法有组间联接法、组内联接法、最近邻元素法、ward法等。笔者采用ward法，以平方欧式距离作为区间进行系统聚类，系统聚类谱系图见图2。

由图2可以看出：当并类距离为1时，样本被分为6类；当并类距离为3时，样本被分为4类；当并类距离为5时，样本被分为3类；当并类距离为25时，凝聚停止，所有样本被归为1类。

2.4 FDA

FDA是一种常用的有监督机器学习，可以对样本的分类进行预测[16]，将系统聚类的结果作为判别模型的分组，定义变量范围1～4，以提取到的主成分作为自变量建立判别函数，其判别函数系数见表3。

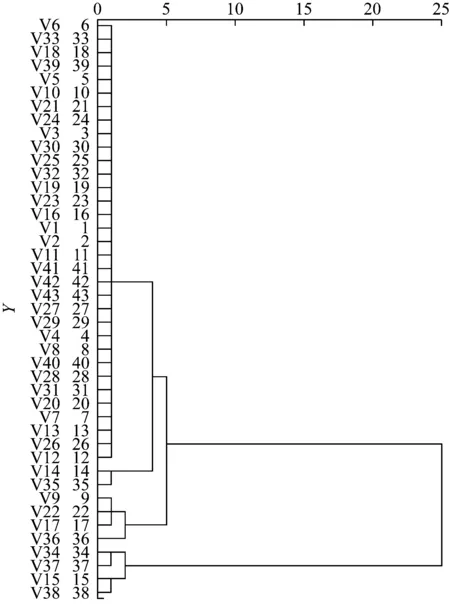
图2 样本的系统聚类谱系图

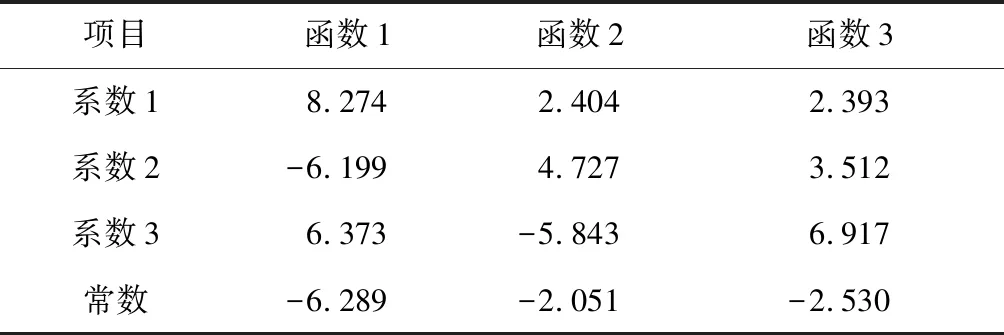
表3 判别函数系数

FDA将高维数据转化到低维空间中进行区分，根据样本间在Fisher判别函数分布图的投影位置来确定分类归属，4个分组的组质心位置见表4。

表4 4个类的组质心位置

建立起的判别函数并不都能较好地实现对样本分类归属的预测，故对3个判别函数的特征值进行分析(见表5)，方差百分比代表函数对样本分类解释能力的强弱。由表5可以看出:第一、第二、第三判别函数的方差百分比分别为88.3%、11.4%和0.2%，第一、第二判别函数显著优于第三判别函数，且第一、第二判别函数的累计百分比达到了99.8%，可以较好地对样本分类归属进行预测，故考虑舍弃第三判别函数。

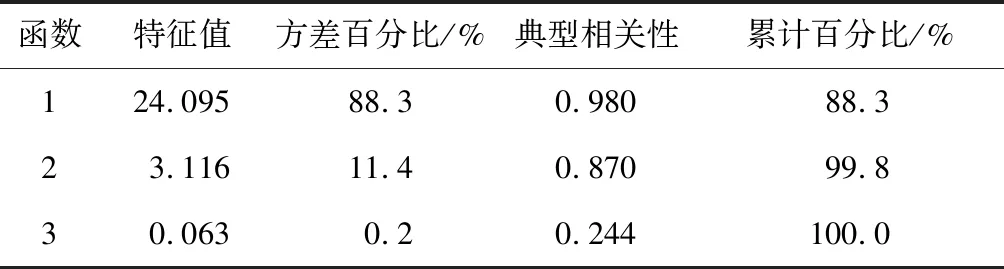
表5 判别函数特征值

为进一步验证上述方法的可行性，引入威尔克Lambda值(见表6)对判别函数进一步讨论，威尔克Lambda值越小，函数影响力越大。

表6 威尔克Lambda值摘要

一般认为当概率小于显著性水平0.05时，认为当前判别函数整体的判别能力较强。由表6可以看出：第三判别函数的显著性水平为0.124，大于0.05，故可以舍弃[17]。以第一、第二判别函数建立联合分布图,见图3。

图3 样本的联合分布图

由图3可以看出：样本在函数1方向区分明显，说明第一判别函数的效果更好，故可以使用第一判别函数对塑料拖鞋鞋底进行分类预测。经交叉验证后，模型的准确率为97.7%，效果较好。

2.5 RBFNN

为消除样本间的量纲关系，首先对已经降维的3个主成分进行标准化，将分组作为因变量，将43个样品以80%和20%的比例随机分配分成训练集和测试集以避免人工分类的误差。输入层神经元为3，输出层神经元为3，隐含层设置为10，激活函数为Softmax，训练次数为3 000。各节点间线段的粗细表示神经元之间相互连接的权重的大小，权重由输入层的3个主成分训练得出。RBFNN结构图见图4，绘制的操作特性曲线见图5。

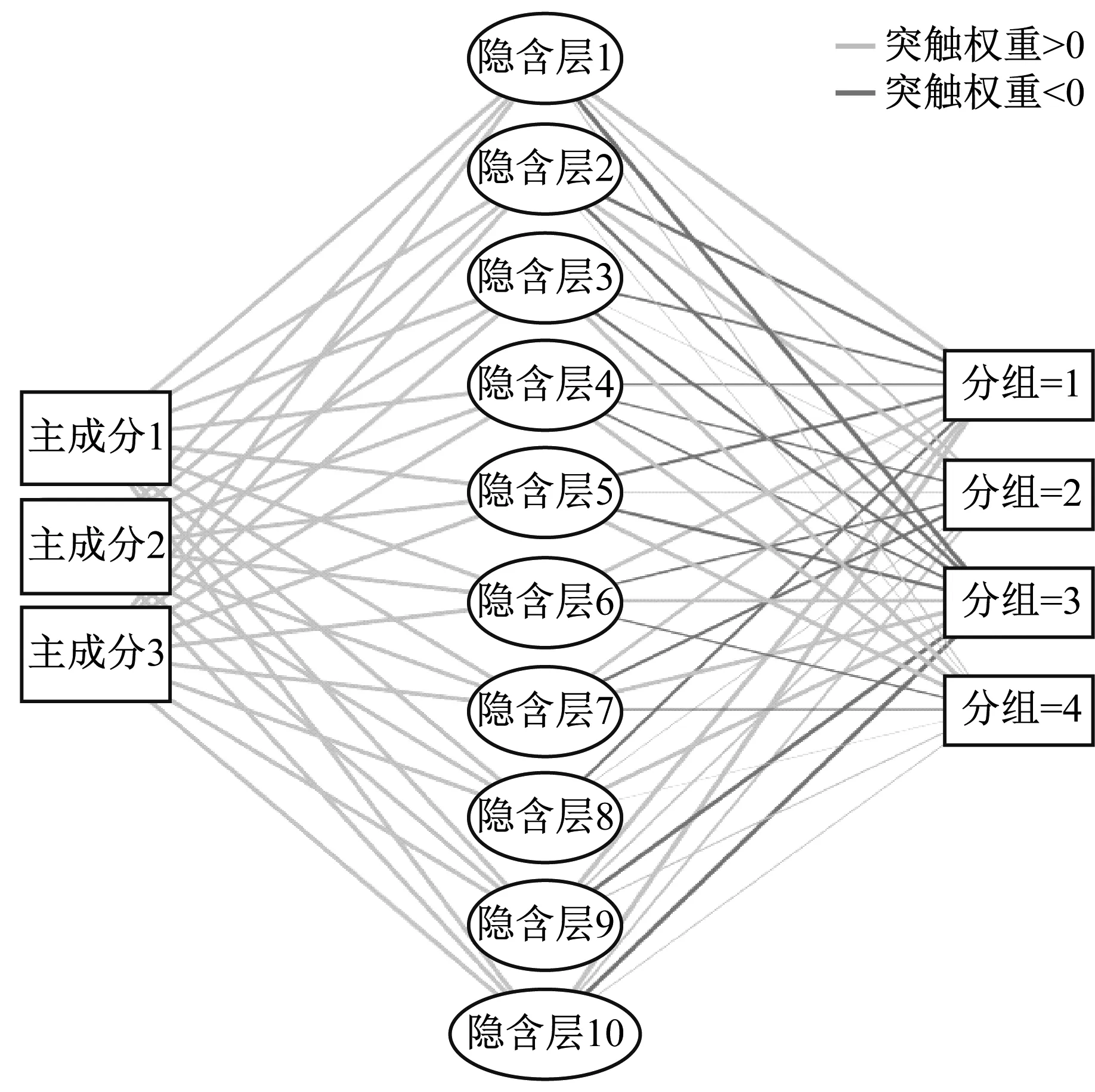
图4 RBFNN结构示意图

图5 模型操作特性曲线曲线

操作特性曲线又称受试工作特征曲线[18]，用以验证某分类器模型性能。对于给出的模型，输入正负类的一组数据，与待测模型对数据的预测进行比对，从而对模型性能进行评估。操作特性曲线的线下面积(AUC)是操作特性曲线的量化指标，AUC越大，分类效果越好。由图5可以得出，4组样品的AUC均为1，诊断准确率高，误判率低。测试集和训练集的准确率为100%，证明可以在已知分类的样品上建立RBFNN模型，对位置样品的归属进行预测。