基于长余辉发光涂料隧道中间段运营亮度检测最优控量研究
2022-08-29席作为饶军应梅世龙陈雪峰苟德明
席作为,饶军应,梅世龙,陈雪峰,陈 军,苟德明,田 娇
(1.贵州大学土木工程学院,贵州 贵阳 550025;2.贵州大学空间结构研究中心,贵州 贵阳 550025;3.贵州大学建筑与城市规划学院,贵州 贵阳 550025;4.贵州省公路工程集团有限公司,贵州 贵阳 550001;5.贵州西能电光科技发展有限公司,贵州 贵阳 550002;6.贵州省交通规划勘察设计研究院股份有限公司,贵州 贵阳 550081)
1 概述
2021年5月19日,交通运输部发布2020年交通运输行业发展统计公报,全国公路隧道21316处、2199.93万延米,增加2249处、303.27万延米,其中特长隧道1394处、623.55万延米,长隧道5541处、963.32万延米[1],隧道已与日常出行密切相关。隧道中间段位置相对封闭,驾驶员的视认效率低于其他路段,容易发生交通事故,且该段发生交通事故对驾驶员逃生和灾难救援造成巨大难度,极易引发二次事故,对驾驶员生命和公共财产安全造成重大危害。路面亮度值是评价隧道交通安全水平的重要指标,掌握亮度值的分布特性对保证隧道运营期间的交通安全至关重要,但隧道长期全天不间断照明会加剧灯具老化,加之汽车尾气、灯具表面积灰等因素使得照明效果大打折扣,故定期对照明系统进行检测尤为重要。当前隧道亮度检测方式效率低下,若完成全部测量任务,工作量巨大,故使用高效测量设备、测量方式或得出亮度检测的最优控量迫在眉睫。
国内外学者对公路隧道照明检测贡献了自己的智慧。王嘉明[2]利用相机进行信息采集,通过数字图像处理技术对眩光进行测量,提高了测量精度,但测试环境较为独特、分析过程耗时;张晓坚[3]针对洞外亮度测量的影响因素进行了研究,提出了基于现场亮度测试方法的公路隧道洞外亮度指标,但试验所选隧道样本量较少,结论不具普适性;郭俊凯[4]设计了可调量程的亮度检测仪,提高了公路隧道亮度检测精度,但对检测仪的操作便捷性、成本需进行考量;郭春等[5]针对隧道洞外亮度的自动测试分析开展了相关研究,提出了基于数码成像技术的公路隧道洞外亮度自动测试方法,但测试结果的分析方法繁琐耗时;王珂[6]基于视频检测技术设计了一套隧道亮度检测系统,但检测过程较繁琐;柳玉良[7]通过数码成像技术对隧道洞外亮度进行了分析,但分析效率较低;杨志武[8]采用数码照片图像分析法对隧道洞外亮度进行测试,但结果输出及分析过程耗时;张翠苹[9]利用车载系统对长隧道内的亮度、照度进行动态检测,但长期使用会影响测量精度;潘冬等[10]利用环境光传感器自适应控制亮度值,消除了亮度突变带来的视觉不适,但并未给出系统的亮度测量方法;秦慧芳等[11]提出了一种基于模糊神经网络算法的隧道照明控制策略,但未考虑行驶车辆对测量精度造成的影响;Li S等[12]提出了一种基于隧道视频监控系统的亮度检测方法,可有效获得隧道大面积探测区域的连续表面亮度参数,但检测视角并非驾驶员第一视角,忽略了灯光角度造成的影响;Yoo S等[13]为了分析道路使用的变化,对隧道路面的阈值区和内区进行了反射率的测量,但并未给出确切的测量点数量。
各类改进的测量仪器、测量方式层出不穷,但存在技术不成熟、成本高、应用面小等缺陷,且受限于地区经济发展状况、隧道运营成本等因素,短期内隧道管理部门仍会采用传统检测方式。显然,沿路面纵向测量得到的数据越多越能更好地反映隧道中间段亮度值的分布特性,但对于长隧道甚至是特长隧道,将亮度值全部测量的工程量巨大,会耗费大量人力物力。因此,如何保证测量数据既能代表总体分布特性,可用于校正和优化隧道照明设计、保证隧道安全运营,又能减少测量人员工作量,这就是研究隧道中间段亮度分布特性及最少检测数量的意义。
研究内容及重点在于对基于长余辉发光涂料隧道中间段亮度进行分布特性分析,求其最少检测数量,并验证结论是否同样适用于普通隧道,故对长余辉发光涂料特性及其施工介绍、使用长余辉材料对原隧道照明效果的提升、测量仪器检测流程、仿真模型建立过程等非重点内容不做赘述。
2 隧道中间段亮度测量
使用照明眩光测量系统对基于长余辉发光涂料照明的牛犁塘隧道中间段路面亮度值进行纵向测量,测量距离依据照明停车视距0取值,共计50m,测量间距1m,隧道内部照明及亮度实测分别如图1—2所示。

图1 隧道内部照明

图2 亮度测量
亮度值的实测数据(升序)见表1。
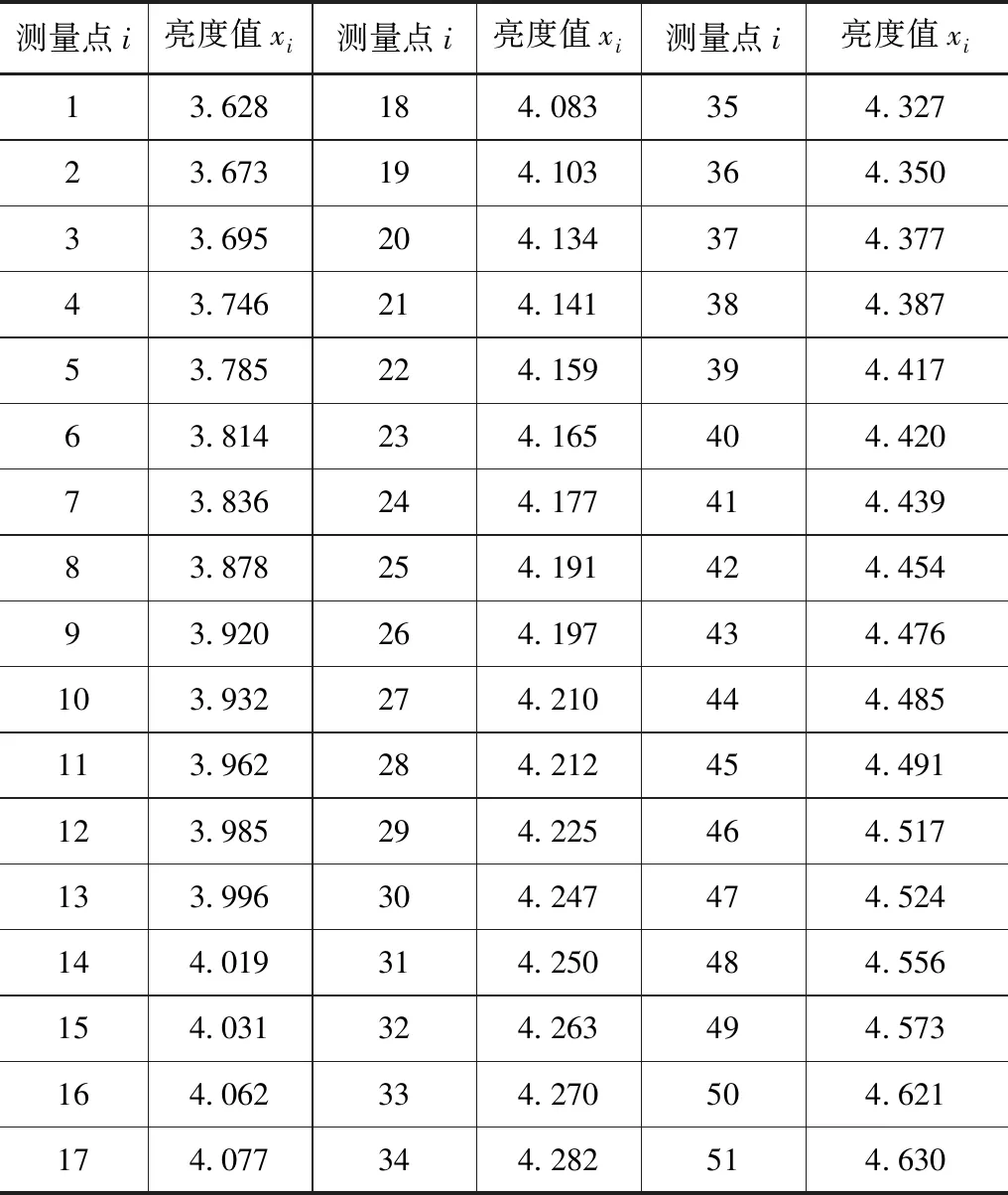
表1 亮度值数据 单位:cd/m2
隧道中间段的亮度值沿纵向分布是均匀的[14],而实测亮度值存在差异,为探究该差异存在的原因,使用仿真模型对该现象进行分析。
3 仿真模型分析
使用AutoCAD和DIALux软件对隧道进行光学仿真模拟,通过路面计算区域内测点的亮度值模拟数据反推实测数据存在差异的原因。由于建模过程不是研究重点内容,故对模型建立过程不做赘述,仅对模型尺寸、材料参数、模拟检测数据进行简要概括,仿真模型伪色图如图3所示。

图3 隧道仿真模型照明伪色图
依据牛犁塘隧道照明工况建立仿真模型,通过调整墙面反射系数模拟长余辉发光涂料的应用[15]。模型长200m,净空高度8m,墙面反射系数0.3;路面宽度7m,反射系数0.1;灯具采用功率为100W的LED灯,双侧交错布置,每侧灯具间隔10m,安装高度5.6m,仰角30°,隧道仿真模型横断面如图4所示。隧道模型长度偏短,为减小因隧道走向、太阳光强度、季节变化等对隧道路面亮度值的影响,且能更准确模拟出隧道中间段亮度特性,在模拟时没有加入日光。
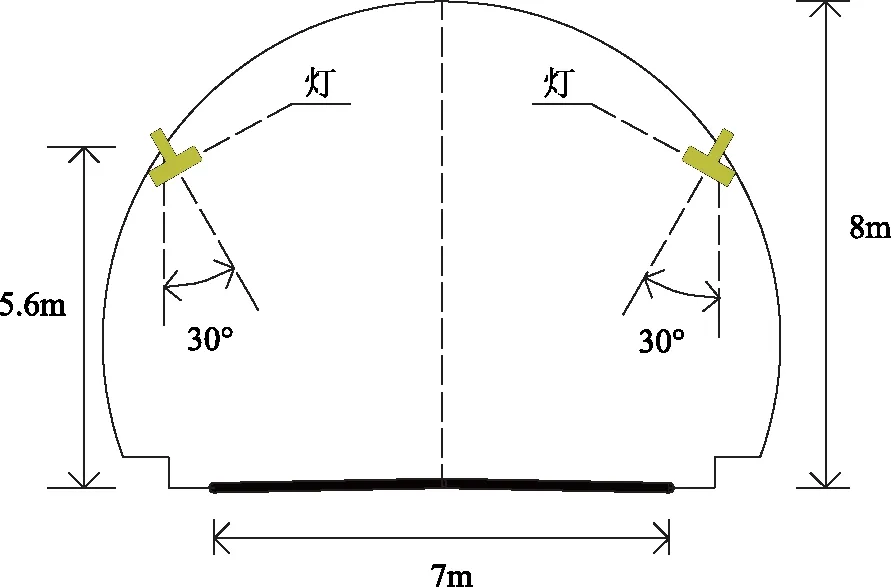
图4 隧道仿真模型横断面
模拟检测时,观测点高度1.5m,横向距离路边缘1/4道路宽度,纵向距亮度计算区域起点60m,观测点偏移1.5°[14]。计算区域横向布设5个测点,为使每个由测点组成的小网格接近正方形且计算区域长度不小于单侧两照明灯具之间的距离,纵向共布置7个测点,故亮度计算区域为一个长12m、宽7m的矩形[16],亮度测量图如图5所示。
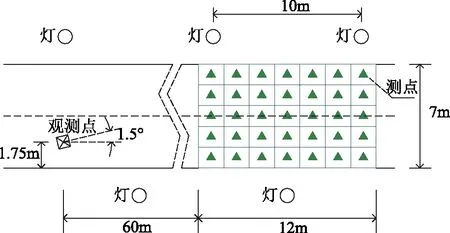
图5 亮度测量图
亮度计算区域内的点亮度值见表2、如图6所示。
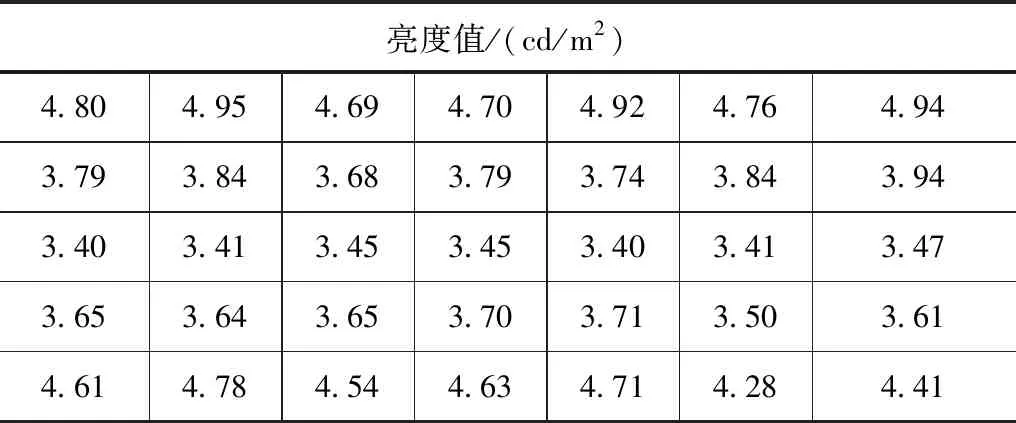
表2 亮度计算区域内的点亮度值
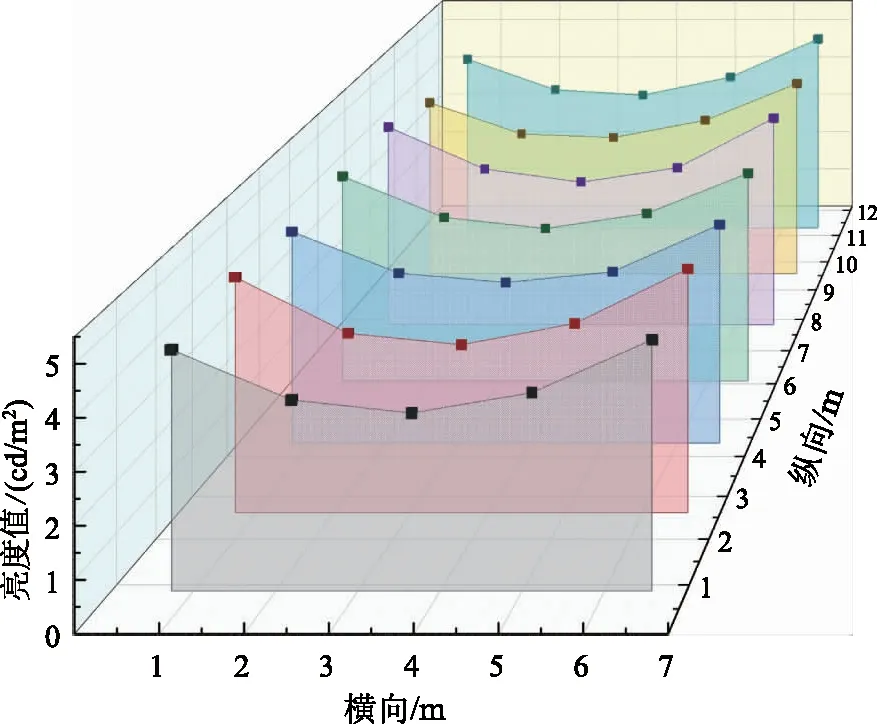
图6 亮度计算区域内的亮度变化
通过表2和图6可知,隧道中间段路面中线亮度低、两侧高,极差为1.55cd/m2,分析路面沿纵向亮度实测值存在差异的原因可能为:隧道墙壁弧度、墙壁反射系数、路面平整度、路面反射系数、灯具安装高度、灯具安装间距、灯具仰角[17]、灯具老化程度等差异对路面亮度带来影响,且亮度测量人员架设测量仪器的位置、高度、角度的不同也会导致测量值存在差异。
4 隧道中间段纵向亮度值的分布特性
首先,对亮度值数据进行初步分析,推测隧道中间段总体亮度可能服从的分布规律。其次,选择一个合适的分布模型,然后对其未知参数进行估计。最后,对选择的分布模型进行假设检验,检验初步分析时的假设是否合理。
4.1 数据的初步分析
在初步分析隧道中间段亮度值的分布特性之前做出以下假设条件:隧道外部环境的变化对中间段路面的亮度值没有影响,亮度仅由照明设施提供。
亮度值的分组频率分布情况见表3。
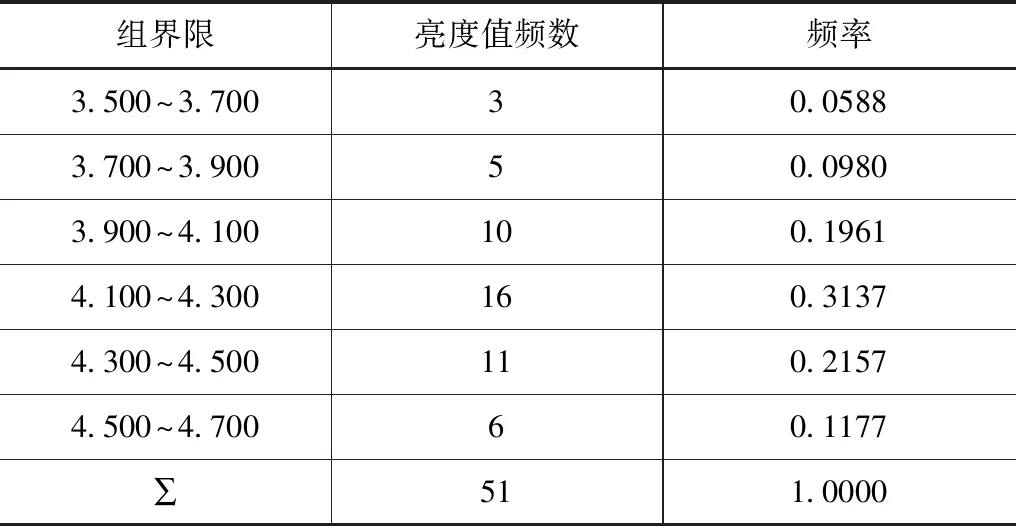
表3 亮度值分组频率
根据亮度值的分组频率分布表画出直方图,如图7所示,顺势画出一条光滑曲线,它的形状与正态分布的概率密度曲线十分相似,故初步认为隧道中间段亮度值总体服从正态分布:X~N(μ,σ2)。
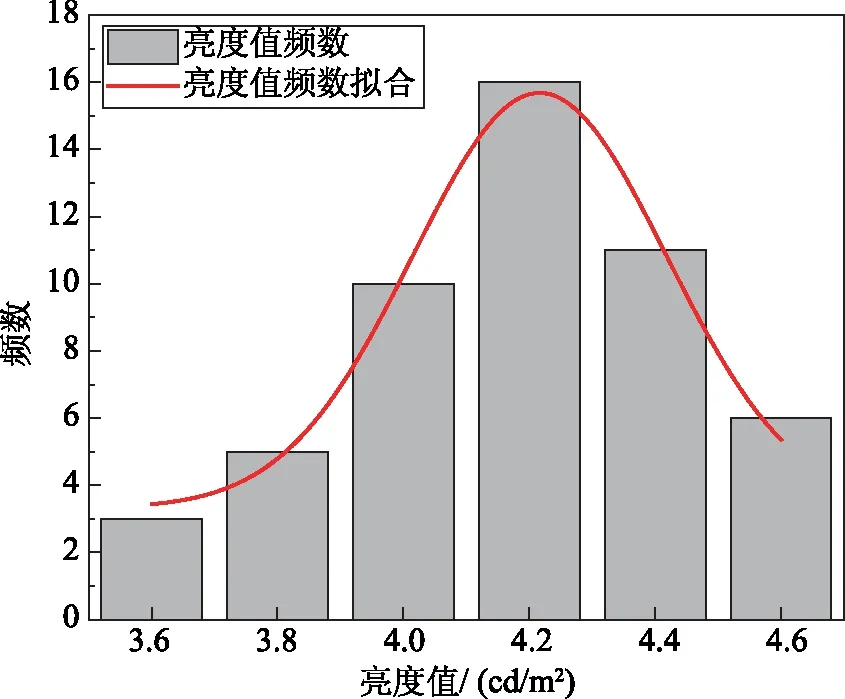
图7 亮度值频率直方图
4.2 参数估计
分布模型已选择,但参数μ,σ2未知,选用点估计法计算未知参数的估计值。
(1)
(2)

4.3 假设检验
隧道中间段亮度值总体X的实际分布函数F(x)未知,根据数据的分析结果推测总体X的可能分布函数为F*(x),对理论分布函数F*(x)进行检验。通过初步分析可知,适合使用皮尔逊χ2检验法进行检验。
将数据按升序排列并分成k个区间,见表4。相比于初步分析时的6个区间,此时区间一端的亮度值数量有所合并,目的为保证每个小区间内的亮度值数量不少于5个。

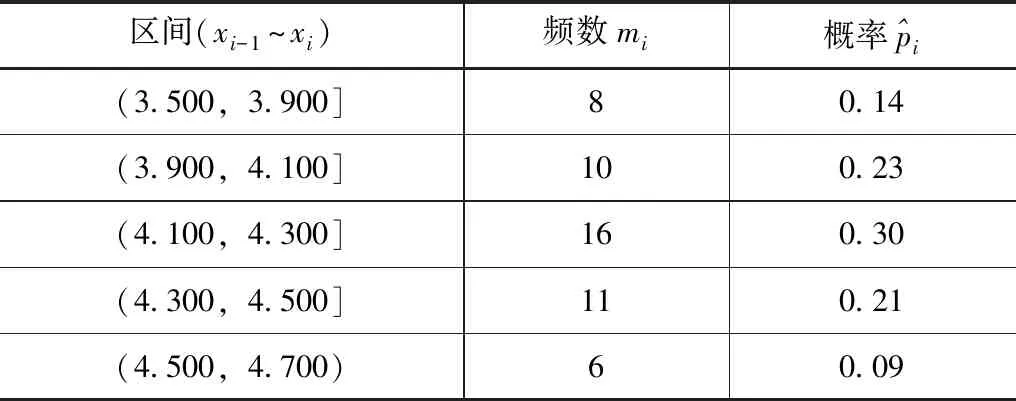
表4 亮度值各区间概率

(3)
式中,k—区间个数;r—F*(x)中待估参数的个数。
所以有χ2~χ2(2),由式(3)得χ2=0.99。
2018汉诺威国际林业木工大会也于同日下午在华召开,来自加工行业的先达数控机械有限公司董事长刘乐球,SFY集团监事会主席John Wang和罗森海姆技术大学Christian Kortum教授等发表主题演讲,为与会者提供家具和木材工业的应用与解决方案的全球视野,阐述了当前木工行业所面临的挑战,即数字化、自动化、物联网平台和个人需求。在2019年汉诺威国际林业木工展览会上,针对于这些挑战,将会有不同的解决方案被展出,帮助观众对家具和木工行业的未来有一个深刻的见解。
小概率事件的概率表达式为:
(4)
式中,α—显著性水平,通常取0.05。
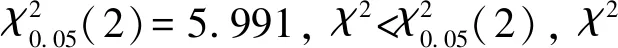
故根据以上分析以及检验可得其分布特性:基于长余辉发光涂料照明的隧道中间段纵向亮度测量值服从正态分布。
5 隧道中间段亮度值的最少测量数量
研究隧道中间段亮度值的最少测量数量的意义在于减少测量人员工作量,同时使该最少测量数据可用于反映隧道中间段的亮度分布特性,判断隧道运营期间的照明是否安全。
在这里称最少检测数量为待检验总体,若原假设不成立,待检验总体的均值μ1与原假设总体的均值μ0肯定会有所不同,存在Δ=|μ1-μ0|,容易犯第二类错误:取伪。故在求最少检测数量的过程中,既要求犯第一类错误的概率α不能太大,也要求犯第二类错误的概率β要尽可能小,即检验功效(1-β)的取值尽可能大。通过同时限定第一类错误与第二类错误来求最能代表亮度值分布特性的最少检测数量,如图8所示。
(5)
(6)
式中,Zβ—临界值在待检验总体分布中的区间点,或标准正态分布概率为β的反函数值;μ1—待检验总体均值。
由式(6)得:
(7)
式中,(1-β)—功效,通常取80%。
由式(5)和式(7)得:
(8)
式中,(μ1-μ0)—待检验总体均值与原假设总体均值的差值,即误差。
原假设总体的均值与标准差均由表1而得,误差取原总体均值的2%,Z1-α/2=Z0.975≈1.960,Z1-β=Z0.8≈0.842,将以上数据代入式(8)并向上取整,得n=85。
在求n时,测量数据个数为有限的小总体,此时需要对n值进行调整:
(9)
式中,n′—调整后的最少检测数量;N—测量数据数量。
由式(9)得:n′=33。
由此可认为,若使隧道中间段亮度值的测量平均值与总体均值的差值不超过2%、置信水平不低于95%、检验功效不低于80%,则最少测量数量为33个。

图8 均值假设检验
6 应用分析
为探究上述基于长余辉发光涂料照明的隧道中间段亮度值最少检测数量的结论是否适用于传统隧道,选取照明方式为传统LED灯的新树洒隧道中间段进行亮度检测,新树洒隧道的照明工况与牛犁塘隧道在使用长余辉发光涂料之前的照明工况类似,亮度检测方法与牛犁塘隧道相同,检测仪器使用相同的照明眩光测量系统,现场测量如图9所示。

图9 亮度实测图
由于最少亮度值测量数量不满足使用皮尔逊χ2检验法的条件,故使用科尔莫戈罗夫检验法。
原假设F(x)=F*(x),在原假设成立的条件下,取统计量:
Dn=sup|Fn(x)-F*(x)|
(10)
式中,Dn—Fn(x)与F*(x)的差异度。
对任意常数λ,记:
(11)
小概率事件发生的概率表达式:
(12)
由式(11)和式(12)得:
Q(λα)=1-α
(13)

表5 亮度值分布
显著性水平α=0.05,由式(13)得Q(λ0.05)=0.95,λ0.05=1.36
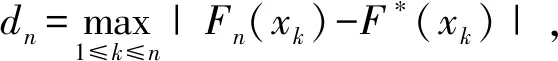
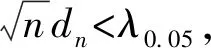
由长余辉发光涂料隧道中间段亮度值得出的最少测量数量结论同样适用于普通隧道,故测量人员在对传统隧道中间段亮度值测量时也可使用以上结论。
7 结论
(1)经仿真模拟,路面亮度计算区域的中线亮度低、两侧高,极差为1.55cd/m2,分析实测亮度值存在差异可能与隧道内壁平整度、路面反射系数、灯具安装和老化、测量仪器位置和角度等因素有关。
(2)对测量数据初步分析、选择分布模型、假设检验,归结出隧道中间段纵向亮度测量值的分布特性为正态分布。
(3)欲知隧道中间段亮度值分布特性并满足测量均值与总体均值的差值不超过2%、置信水平不低于95%、检验功效不低于80%,则亮度值测量数量不应低于33个,且该结论对使用传统照明方式的普通隧道同样适用。
(4)对隧道中间段照明建设以及亮度检测提出以下建议:灯具安装高度、角度、间距应尽可能保持一致;亮度测量仪器的位置、高度、角度应可能保持一致。
