基于AHP-OWA-EM-FUZZY模型的西藏高原典型小流域水资源承载力研究
2022-08-29文梅君彭明勇刘国勇张位首
文梅君,余 江,彭明勇,刘国勇,张位首
(1.西藏自治区水利电力规划勘测设计研究院,西藏 拉萨 850000;2.四川大学,四川 成都 610000)
目前,我国水资源短缺问题突出,主要分为资源型缺水、工程性缺水和水质性缺水3大类[1]。水资源承载力是对水资源安全的一个基本度量,研究水资源承载力对于认识和建设水资源安全保障体系具有重要意义。近年来,国内外学者开展了各种单一模型、复合模型的水资源承载力相关研究[2- 9],但是相关专家、学者对西藏高原流域的水资源承载力研究较少。现阶段关于西藏的雅鲁藏布江[10]、拉萨河[11]、澜沧江[12]、金沙江[13]等大江大河研究比较多,而西藏有大量小流域,且小流域中有许多人口、牛羊、耕地、林地、草地分布,但是针对小流域的研究却比较少。2014年以来,西藏先后启动了多个流域,包括中小流域的综合规划编制工作[14],对流域进行统筹管理,迫切需要对西藏高原流域进行水资源承载力深入研究。
1 西藏高原典型流域概况
西藏河流众多,流域面积100km2及以上河流3361条;流域面积1000km2及以上河流331条;流域面积10000km2及以上河流28条[15]。本文选取的6条典型流域包括西藏东部的金沙江右岸一级支流嘎托河流域、西藏中部的雅鲁藏布江左岸一级支流湘河流域、西藏西部阿里地区KHL、西藏北部的怒江二级支流索曲左岸一级支流连曲(巴青曲)、西藏东部怒江一级支流冷曲、西藏东部怒江右岸一级支流昌西曲(舍曲河)。6条流域分布在那曲市、昌都市、林芝市、阿里地区、日喀则市,占西藏七个地市中的5个地市,地市涉及率达到70%以上。6条流域遍布了西藏东部、中部、西部,因此选取的6条流域具有典型性。
本文数据基准年为2015年,采用《2016年西藏统计年鉴》《2016年昌都市统计年鉴》《2016年日喀则市统计年鉴》《2016年阿里地区统计年鉴》《2016年林芝市统计年鉴》、流域综合规划和《2015年西藏水资源公报》等数据,统计6条流域的自然资源、社会经济和水资源状况。
2 西藏高原典型流域水资源承载力评价指标体系的建立
2.1 总体思路
决定水资源承载力状况的是一个复杂的耦合的系统,这个耦合的系统主要包括资源禀赋、社会经济、生态环境等[16]。对流域水资源承载力进行评价就需要定量分析水资源承载力状况,全面系统分析资源禀赋、社会经济、生态环境的相互关系,初步筛选出各个子系统对应的量化指标。结合西藏高原流域特点,筛选出反映西藏高原流域水资源承载力的评价指标。评价指标数量不宜太多,一般每个系统评价指标建议不超过10个,7—9个最好[17]。对评价指标体系进行量化分级,确定其权重,从而科学合理构建水资源承载力指标体系。
2.2 指标体系的选取分析
根据以上思路,本研究把西藏高原流域水资源承载力指标体系分为3个层次5个大类28项具体指标。评价指标为正向时,其值越大,承载力越强;评价指标为逆向时,其值越大,承载力越弱[18]。3个层次分别为目标层(A)、准则层(B)、指标层(C)。目标层(A)为西藏高原典型流域水资源承载力。准则层的建立本着从宏观全面反映与水资源承载力相关的资源、社会、经济、生态等情况,同时结合用水总量控制、用水效率控制、水功能区限制纳污控制这“三条红线”的要求和最严格水资源管理制度的内容,把水功能区限制纳污这条红线对应指标归入生态环境准则层中,因此准则层分为5个大类,分别为资源禀赋(B1)、社会经济(B2)、生态环境(B3)、用水总量(B4)、用水效率(B5)。指标层共计28项,详见表1。为便于评价指标的分级,反映各指标相对大小,利于横向比较各流域中相应指标,总体来说大部分指标基本是一个比值。
2.3 指标体系的分级
为研究西藏高原典型河流的水资源承载力,需对评价指标建立评价等级,评价等级建立得是否科学合理将影响水资源承载力评价结果的可靠性。
由于西藏的水资源禀赋、社会经济、生态环境、生产生活方式和全国相比具有相当大的差异性,参考现有的水资源承载力指标体系分级研究[19],结合西藏自治区省级行政区划28个评价指标的平均状况,建立评价指标分级体系,见表2。
本文假设西藏自治区省级行政区的28个评价指标基本处于V2等级,将西藏高原典型流域水资源承载力28个评价指标划分为V1、V2、V3三个等级,详见表3。V1表明水资源承载力好,V2表明水资源承载力一般,V3表明水资源承载力差。“+”说明该指标为正向性指标,指标数值越大,水资源承载状况越好。“-”说明该指标为负向性指标,指标数值越大,水资源承载状况越差。
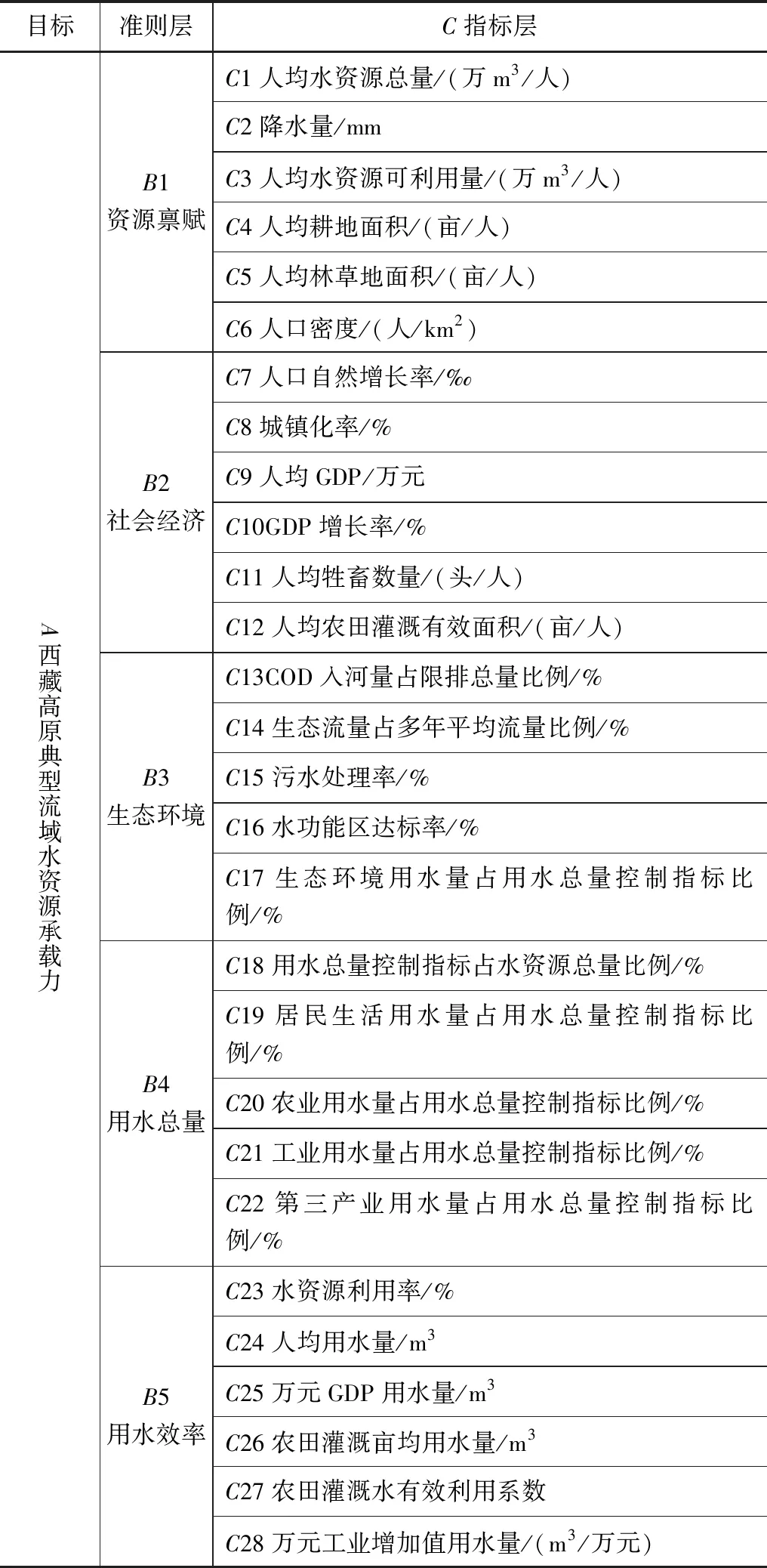
表1 西藏高原典型流域水资源承载力评价指标体系
3 AHP-OWA-EM-FUZZY模型构建
首先通过层次分析模型(AHP)及单因素方差分析(One Way ANOVA)建立与西藏高原典型流域水资源承载力评价指标体系相应的主观权重;其次,根据西藏东部、中部、西部的典型流域的现状,用熵值模型(Entropy Method)建立指标体系的客观权重。综合权重为层次单因素方差模型(AHP-OWA)和熵值模型(EM)的算术平均值。
把求得的综合权重作为模糊综合评价模型(FUZZY)的输入项,通过构造隶属度函数和模糊评价矩阵,计算综合评价指数。
3.1 层次单因素方差分析模型(AHP-OWA)
层次分析法(AHP)能综合定性和定量2方面的指标,将人的主观判断用数量表达出来,应用广泛。由于人的主观判断得出的权重可能有很大的差异性,为了避免主观判断的差异性,用单因素方差分析法对专家主观判断的权重进行分析,以保证主观权重数据的合理性和有效性。
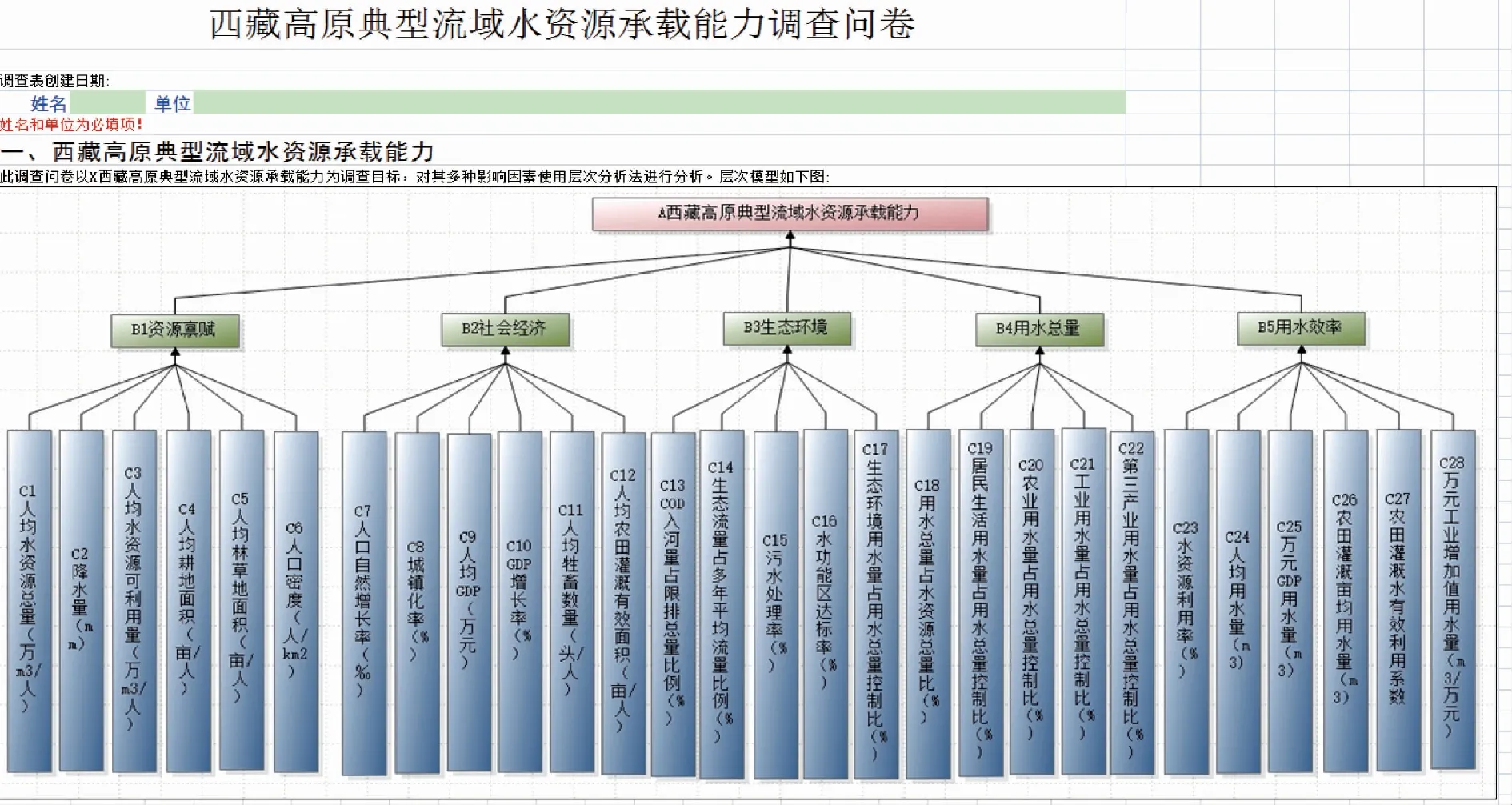
采用美国运筹学家T.L.Saaty教授于20世纪70年代初期提出的层次分析法(AHP)[20],把建立的研究目标的指标体系表1在yaahp软件上建立层次结构模型,生成AHP专家调查表,如图1、图2所示等,第3层要素调查表在yaahp软件上。
咨询专家填写AHP模型相对重要性调查表。本研究共咨询了10位西藏水资源权威专家,分析了水资源承载力并对指标层和准则层的重要性进行判断。咨询的专家中,副教授2位,高级工程师2位,工程师6位。
建立判断矩阵并求特征值和权重,对判断矩阵进行一致性检验。首先根据每位专家填写的AHP模型相对重要性调查表,计算每位专家指标层中指标对A目标层的权重排序。

表3 西藏高原典型流域水资源承载力评价指标分级
使用yaahp软件的群决策对专家数据进行分析。设每5个专家为一个群决策组,每个群决策组中有1位副教授、1位高级工程师、3位工程师,因此把10个专家分为群决策组J1、J2。把2组群决策结果的权重进行EXCEL“数据分析”中的单因素方差分析(One Way ANOVA),判断两组数据的差异显著性水平。如2组数据差异性不显著,则专家主观判断取得的权重可信。
每组群决策计算结果详见表4。Wj1′为群决策组J1对指标层C的权重,Wj2′为群决策组J2对指标层C的权重。对Wj1′、Wj2′2组数据采用算术平均法计算层次模型权重得到Wj′。Wj1′、Wj2′的数据趋势分布如图3所示。通过分析,群决策组J1、J2由层次分析法得出的权重较大的指标集中在B1、B3、B5准则层,且2组数据权重趋势具有一致性。
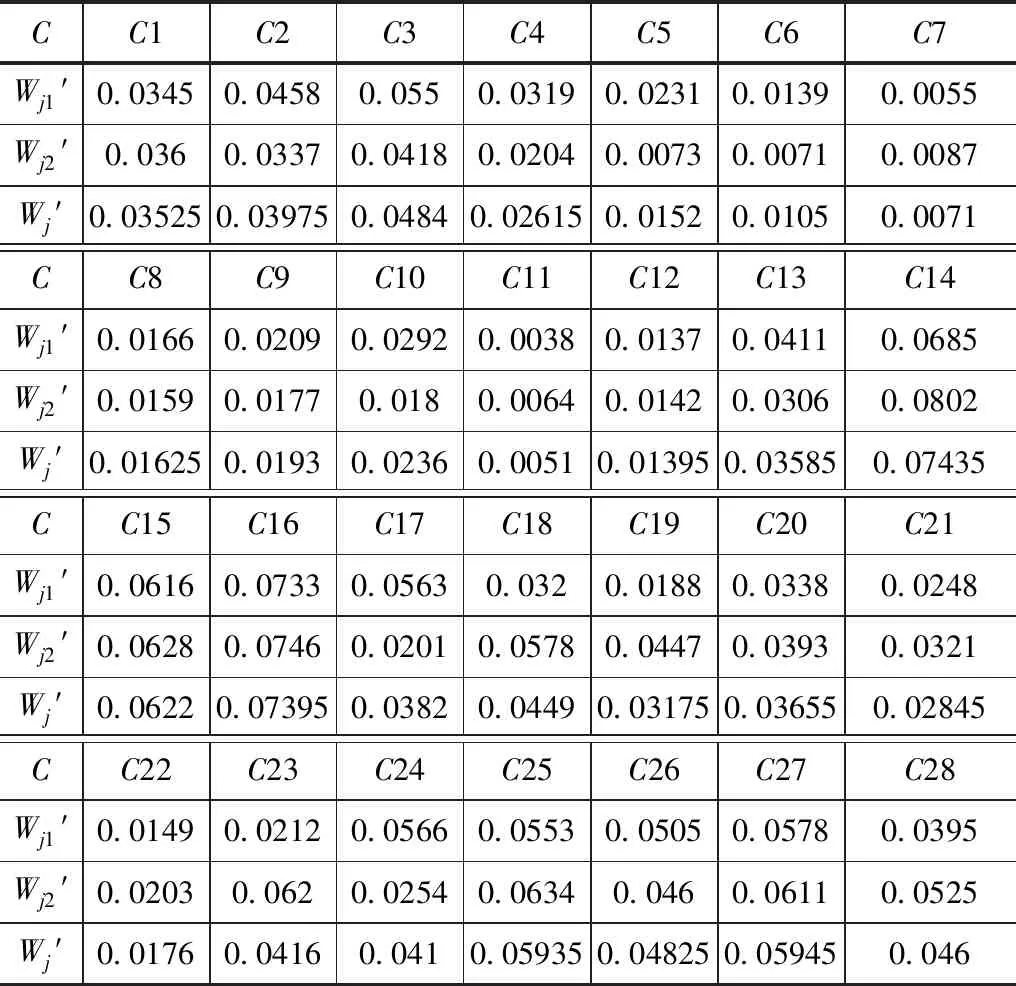
表4 C指标层中指标对A目标层的权重(Wj1′、Wj2′、Wj′)
由于专家在填写调查问卷的主观性强,现用单因素方差分析法对专家主观判断的权重进行分析,从而判断层次分析法2组群决策专家组调查得出的权重是否有效。
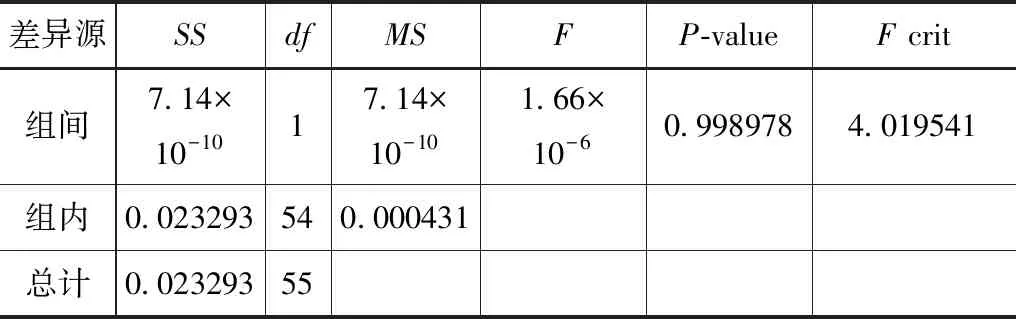
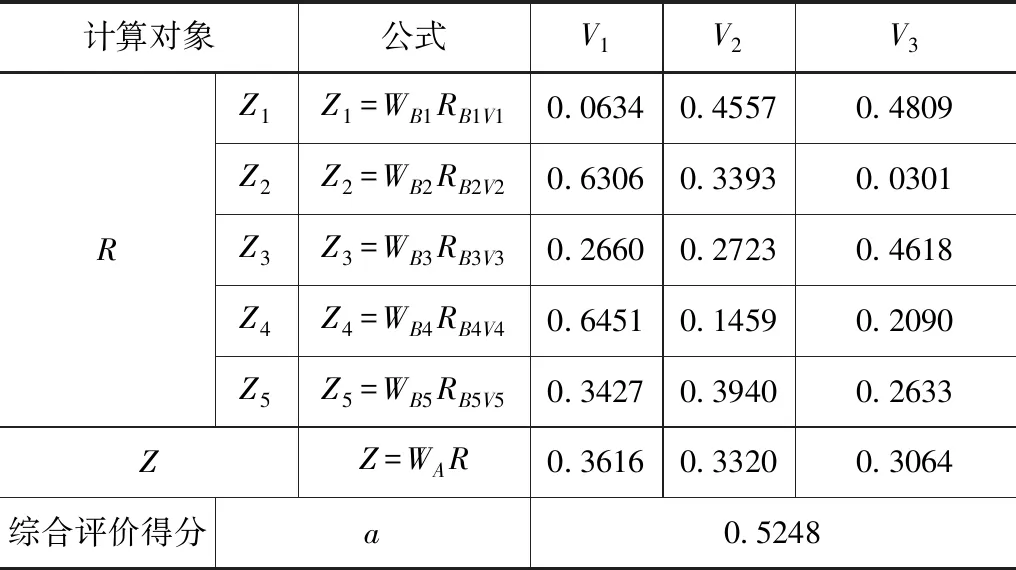
采用EXCEL单因素方差分析,以α=0.05及95%的可靠性推断,得出方差分析结果,见表5。得出F 熵值法是计算权值的一种客观方法。在赋值过程中没有人为主观因素加入,依靠实测和统计资料通过对数据计算确定评价指标权重,能相对真实地反映出指标之间的关系。确定权重的步骤如下: 表5 Wj1′,Wj2′单因素方差分析结果表 图1 西藏高原典型流域水资源承载力调查表 图2 西藏高原典型流域水资源承载力调查表 图3 Wj1′,Wj2′趋势分布图 (1)建立有m个样本、n个评价指标实测或统计的数据的矩阵: R=(xij)m×n(i=1,2…,n;j=1,2,…m) (1) (2)把样本数据矩阵进行非负化处理,同时为了避免求熵值得出无意义的数据,同时平移数据,非负化公式如下: (2) 式中,指标bij越大越优。 (3) 式中,指标bij越小越优。 (3)由B=(bij)m×n计算j项指标下第i个样本占该指标的比重Pij: (4) (4)第j个评价指标的熵为: (5) (6) (5)计算评价指标的权重: (7) 各指标的权重满足指标的熵越大,其熵权越小,该指标越不重要,而且满足: (8) AHP模型得出的各评价指标的权重为专家、学者的主观判断。熵值模型计算的各评价指标为典型流域的客观权重。为使权重的确立更加科学有效,因此用综合权重计算评价指标。综合权重为层次单因素方差模型(AHP-OWA)和熵值模型(EM)的算术平均值。 计算公式如下: (9) 评价指标的综合权重结果如下: B1、B2、B3、B4、B5对目标A的权重为WA=(0.2026,0.1555,0.2209,0.1576,0.2635); 在资源禀赋B1中,C1、C2、C3、C4、C5、C6对目标B1的权重为WB1=(0.2195,0.1767,0.2602,0.1418,0.1758,0.0260); 在社会经济B2中,C7、C8、C9、C10、C11、C12对目标B2的权重为WB2=(0.1203,0.1571,0.1781,0.2281,0.1404,0.1759); 在生态环境B3中,C13、C14、C15、C16、C17对目标B3的权重为WB3=(0.1577,0.3147,0.1408,0.1674,0.2194); 在用水总量B4中,C18、C19、C20、C21、C22对目标B4的权重为WB4=(0.2352,0.2064,0.2151,0.1877,0.1556); 在用水效率B5中,C23、C24、C25、C26、C27、C28对目标B5的权重为WB5=(0.1384,0.1473,0.1828,0.1951,0.1702,0.1662); 评价指标层C对目标层A的综合权重WAC=(0.0445,0.0358,0.0527,0.0287,0.0356,0.0053,0.0187,0.0244,0.0277,0.0355,.0218,0.0274,0.0348,0.0695,0.0311,0.0370,0.0485,0.0371,0.0325,0.0339,0.0296,0.0245,0.0365,0.0388,0.0481,0.0514,0.0448,0.0438)。 其中综合权重大于0.04以上的从高到低依次为:C14,C3,C26,C17,C25,C27,C1,C28,这些指标属于资源禀赋、生态环境和用水效率准则层,说明在西藏高原典型流域水资源承载力影响因素中,B1、B3、B5的作用更为突出。 1965年,美国L.A.Zadeh教授提出了模糊集合论[22]。模糊综合评价法是以模糊数学隶属度的基本理论为基础,为了某种目标,考虑多种因素的综合影响,对复杂问题做出决定的综合评价方法。总的来说,模糊综合评价法是通过评价因素集、对应评语集通过隶属度函数构造模糊矩阵,从而综合了评价对象的评价因素信息,得出评价结果,避免了单指标评价信息流失[23]。 3.4.1设立评价因素集 建立西藏高原典型流域水资源承载力评价因素集。因素集是评价对象的各评价因素的集合。设C={C1,C2,…Cn},Ci(i=1,2,…n)为评价因素。本文根据西藏高原典型流域的特点,设置28个评价指标(因素)。其中A代表西藏高原典型流域水资源承载力这个目标。设A=(B1,B2,B3,B4,B5),其中Bi为准则层构建的评价因素集。 设B1=(C1,C2,C3,C4,C5,C6); B2=(C7,C8,C9,C10,C11,C12); B3=(C13,C14,C15,C16,C17); (10) B4=(C18,C19,C20,C21,C22); B5=(C23,C24,C25,C26,C27,C28)。 3.4.2设定评价因素的评判集 评价对象为西藏高原典型流域,包括昌西曲、嘎托河、冷曲、连曲、湘河、KHL。对评价对象根据评价因素属于评价分级标准的相应等级做出评语的集合为评判集,如下: V=(V1,V2,…Vm) (11) 式中,V—C中各因素对应评价等级的集合。 3.4.3建立评价因素的权重 评价因素的权重为层次单因素方差模型(AHP-OWA)和熵值模型(EM)的算术平均值求得的综合权重: (12) 3.4.4构造等级之间能平滑过渡的隶属度函数[24] 隶属度函数能使各评价指标相差不大的数值或者相差很大的数值通过模糊化处理后,各指标能在等级间平滑过渡[25]。本文评判集划分为3个等级V=(V1,V2,V3)。 因此设评价因素对评判集的隶属度函数为[26]: (13) (14) (15) 设k1为V1与V2的临界值,k3为V2与V3的临界值,k2为V2水平区间中点值[27]。当评价因素越小,水资源承载力越好时,采用式子(13)至(15)计算隶属度函数。如评价因素越大,水资源承载力越好时,需将上式右边的所有区间号改变方向,即大于改成小于,小于等于改成大于等于,再用来计算评价因素的隶属度函数。 3.4.5根据隶属函数构造评价因素与评判集的隶属度矩阵 根据隶属度函数,定义评价因素集中B中的第i个元素Ci(i=1,2,…,n)对应评判集中的第j个元素(j=1,2,…,m)的隶属度为rij,把评价因素集为维度构造模糊矩阵R如下: (16) 3.4.6模糊综合评价计算 由加权模型,模糊综合评价可以表示为: Z=WR,Z=(z1,z2,…zj…zn),zj∈[0,1] (17) 式中,W—下一层指标相对于上一层指标的权重;zj—等级Vj对Z的隶属度,表示模糊综合评价结果。 再赋予评判集中各等级分值aj,设V1等级中a1=0.95,V2等级中a2=0.50,V3等级中a3=0.05。用下式计算水资源承载力的综合评分值及水资源承载力准则层的综合评分值a。a值越高,水资源承载力的潜力越大。根据AHP-OWA-EM-FUZZY模型及评价指标分级标准设计,V2等级约为西藏水资源承载力平均水平。 (18) 根据AHP-OWA-EM-FUZZY模型,由公式(17)可以求得5个准则层的模糊综合评价结果,见表6—11。 表6 嘎托河流域水资源承载力模糊综合评价结果表 表7 湘河流域水资源承载力模糊综合评价结果表 表8 KHL流域水资源承载力模糊综合评价结果表 表9 昌西曲流域水资源承载力模糊综合评价结果表 表10 连曲流域水资源承载力模糊综合评价结果表 表11 冷曲流域水资源承载力模糊综合评价结果表 4.2.1从流域属于的等级分析 根据表6—11,Z值对V1等级隶属度最大的有昌西曲、嘎托河、连曲,说明昌西曲、嘎托河、连曲水资源承载力处于较好的状态;Z值对V2等级隶属度最大的流域有冷曲、KHL,说明冷曲、KHL水资源承载力处于一般的状态;Z值对V3等级隶属度最大的流域有湘河,说明湘河水资源承载力处于较差的状态。 4.2.2从流域水资源承载力模糊综合评价得分分析 西藏高原6条典型流域水资源承载力得分详见表12。得分越高,水资源承载力越强。西藏高原典型流域水资源承载力模糊综合评价得分从高到低依次为昌西曲、连曲、嘎托河、KHL、冷曲、湘河,说明昌西曲流域水资源承载力最好,湘河水资源承载力相对比较差。 表12 西藏高原典型流域水资源承载力模糊综合评价得分表 4.2.3从流域所处的地理位置分析 西藏地域面积广阔,资源禀赋、社会经济、生态环境状况从东到西、从北到南差异性极大。本文把西藏高原6条典型流域从林芝市所在地的经度分为东面3条流域、西面3条流域分别分析其水资源承载力。林芝市东面3条流域所处地理位置为藏东,从南到北分别为昌西曲、嘎托河、冷曲。林芝市西面3条流域所处地理位置为藏中和藏西北部,从南到北分别为湘河、KHL、连曲。在藏东从南向北,昌西曲、嘎托河、冷曲的水资源承载力逐渐降低。在藏中和藏西北部从南向北,湘河、KHL、连曲的水资源承载力逐渐升高。如图4所示。 图4 西藏高原典型流域水资源承载力趋势图 4.2.4从准则层分析 从准则层分析,社会经济、用水总量得分相对较高。资源禀赋、生态环境、用水效率得分相对较低,如需提高西藏高原流域水资源承载力的安全保障能力,需从这3个方面着力。 由于水资源承载力是由多系统综合作用决定的,难以简单归纳说明某一方面的因素决定水资源承载力高低。但是本文研究发现,西藏高原6条典型流域水资源承载力高低和用水效率水平高低呈现基本一致性。 本文构建适合西藏高原不同流域的水资源承载力评价模型(AHP-OWA-EM-FUZZY),通过建立评价指标量化评价研究西藏高原典型小流域的水资源承载力,对西藏高原小流域的水资源优化配置、提高高原流域的水资源承载能力、更有效地提高农牧民生活用水、一产二产三产用水、生态用水的保证率具有很好的借鉴作用,为我国水资源承载能力评估指南建立提供基础资料。 由于西藏高原流域基础数据的缺乏本文仅选取了西藏高原6条典型小流域进行空间研究。在空间区域上,未来可以增加西藏高原典型流域的数量,以建立更完善的适合西藏高原典型流域水资源承载力体系,研究各流域水资源承载力的差异性及共性,更好地为流域综合管理与规划服务。3.2 熵值模型[21]


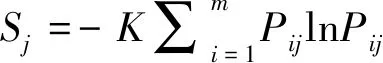
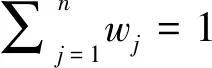
3.3 综合权重及计算结果
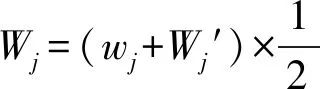
3.4 模糊综合评价模型

4 评价结果及分析
4.1 6条典型流域水资源承载力的综合评价结果
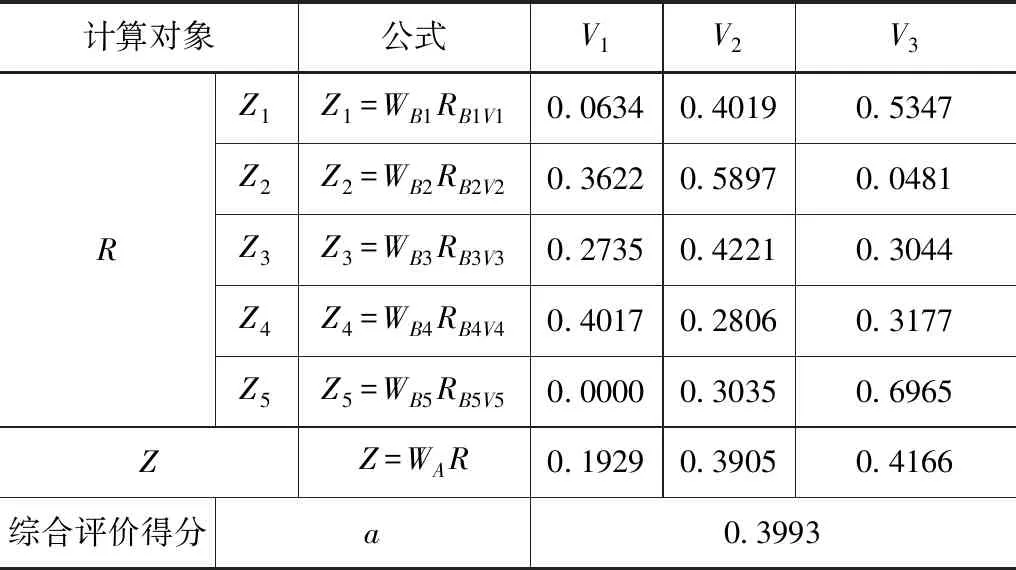
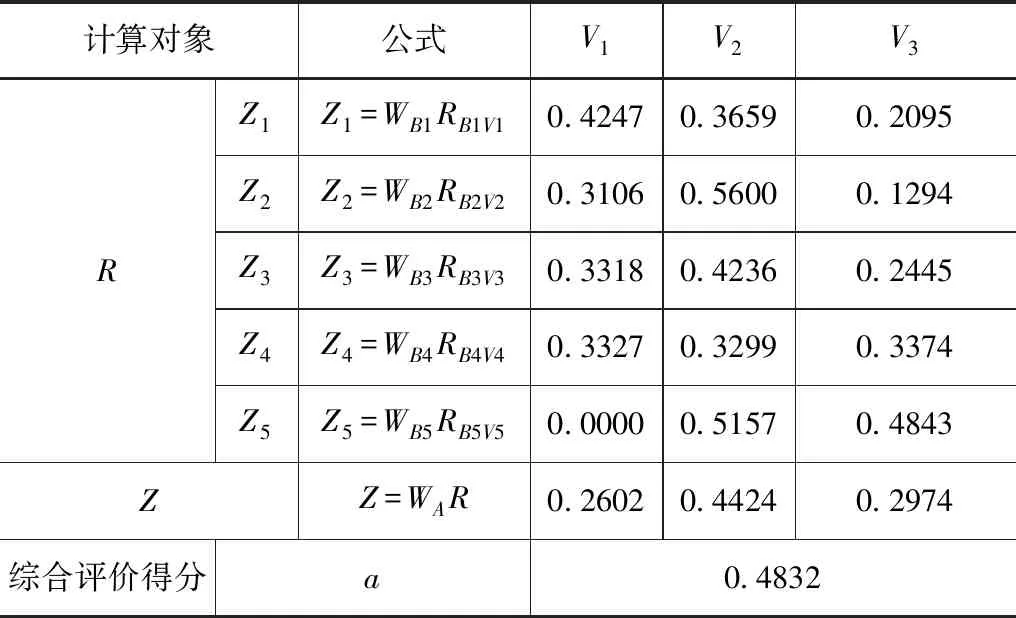

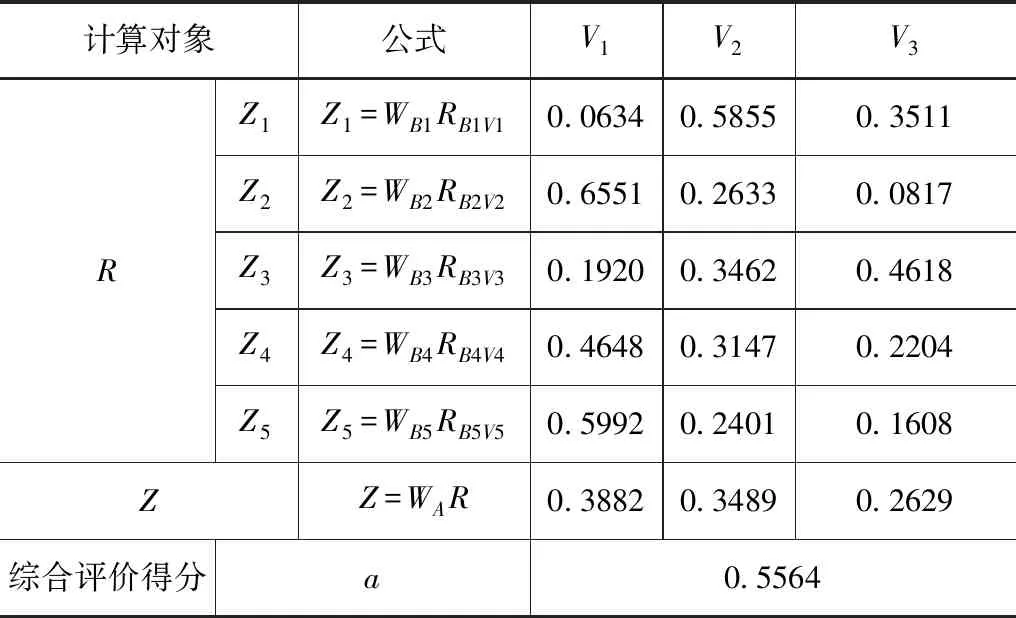

4.2 6条典型流域水资源承载力综合评价结果分析


5 结论
