基于单相dq 0变换的双电源转换开关电压故障检测

欧阳俊峰, 迟长春, 陆彦青

(上海电机学院 电气学院, 上海 201306)

随着社会经济的不断发展,人们对供电的可靠性及质量有了更高层次的要求。双电源转换开关作为保障系统供电可靠性的一个重要手段,其转换时间是一个重要指标。电源转换时间越快,供电可靠性越高[1-4]。目前,市场上双电源转换开关结构已趋于成熟,对电压的故障检测算法进行优化可以一定程度地减少转换时间。在电压故障检测算法领域中,从传统的有效值法到应用比较广泛的基于瞬时无功理论的dq0变换法,以及傅氏变换法,再到近几年发展起来的小波变换法,各类算法层出不穷。这些算法在检测电压上都有一定的局限性。例如,文献[5-8]采用有效值法对电压进行检测,利用工频周期内的电压求得的有效值监测电压的变化来判断是否发生故障,但是需要1个周期的电压数据以得到有效值,因此在检测时间上有延时性。文献[9-12]通过傅里叶变换将电压周期信号分解为离散频谱,再进行积分求和得到电压幅值,虽然傅氏算法可以过滤高次谐波使得采样电压精度较高,但是也需要1个周期的电压数据,其算法速度和有效值法一样缓慢。文献[13-15]将三相电压从abc坐标变换到dq0坐标下求得电压幅值,但是该算法只能用于三相故障检测,若出现单相故障时,dq0算法将检测不准确,且算法中的滤波器时间常数也会使反应时间延迟。

为此,本文研究了一种电压故障检测的方法,通过卡尔曼滤波算法对采样信号去噪,对去噪后的单相电压重新构建三相电压,同时用导数滤波法省去了低通滤波器的使用。仿真结果验证了本文方法解决了低通滤波器的时间延迟问题。

1 基于卡尔曼滤波算法的电压采样方法

电压故障检测是通过采集电源电压信号,实时监测电压的幅值变化来判断电源是否发生故障。因此,提高电压采样精度能够加强对白噪声的抗干扰能力,可以有效避免因电压误差导致的电压故障检测失误,提升装置的供电可靠性。为提高电压采样精度,通过Matlab结合卡尔曼滤波算法进行去噪处理,减少了采样电压的读取误差。

卡尔曼滤波在线即时利用控制变量和预先递推估算的值还原真实数据,其具有动态跟踪能力强、估计精度高、计算方法简单,以及在计算机上实现迭代递推计算的优点。鉴于电压采样信号中包含谐波分量、测量误差等噪声,本文采用卡尔曼滤波算法,能以极短的时间从电压采样信号中提取出基波分量,且卡尔曼滤波算法有较高的运算精度。卡尔曼算法流程如图1所示。

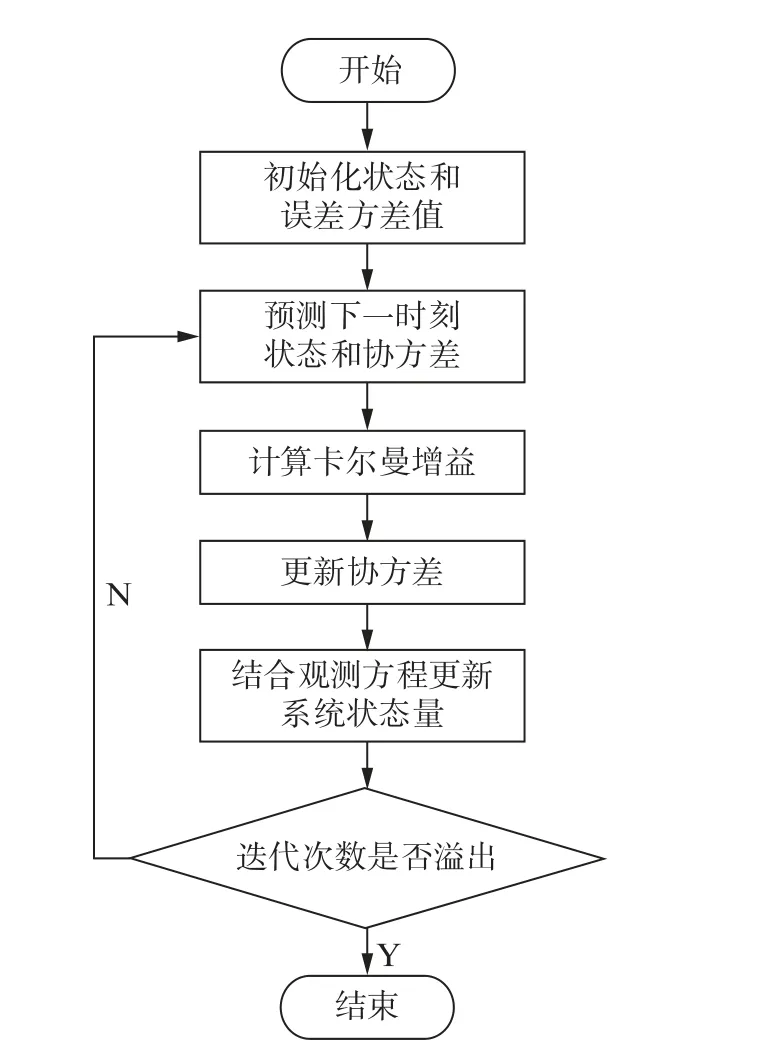
图1 卡尔曼算法流程

系统某一时刻的状态方程和测量值分别为

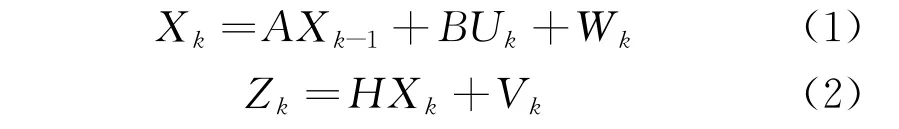
式中:X k为k时刻的系统状态;X k-1为k-1时刻的系统状态;U k为k时刻的系统电压值;Wk为k时刻的过程噪声;A、B为系统参数;Z k为k时刻系统测量值;H为测量系统参数;V k为k时刻测量噪声。

卡尔曼滤波估测过程分为预测和更新两部分。先在预测阶段利用k-1时刻的状态,预测k时刻的预测值为

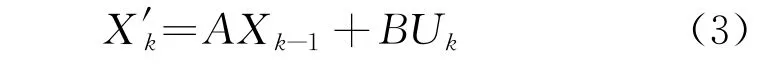
由于X k的协方差未更新,利用k-1时刻的协方差最优估计值P k-1,预测k时刻协方差最优估计值为

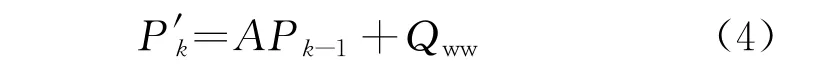
式中:Qww为系统过程协方差。

在更新最优估计值部分中,首先计算卡尔曼增益K k,再根据K k对系统状态和误差协方差进行校正,获得该时刻的最佳估计值,方程组为

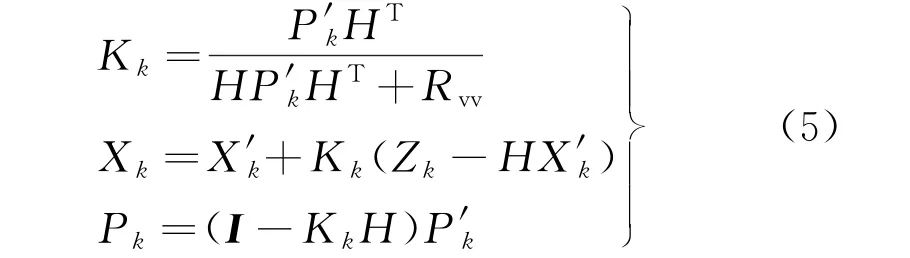
式中:Rvv为系统测量协方差;P k为k时刻误差协方差最优估计值;I为单位矩阵。

当系统进行下一时刻运算时,P k→P k-1。卡尔曼滤波算法能自行回归运算,在迭代中消除噪声,得到更接近实际的电压值,这有利于为电压故障检测提供更精确的电压采样值。

2 电压故障检测方法

通过混合式双电源转换开关控制器,利用卡尔曼滤波算法去噪后得到的电压,检测电源电压是否有断相、过压、欠压和三相不平衡等多种故障,若电源发生故障则控制器产生指令信号,转换开关执行相对应的动作。对电源突发电压变化的情况,双电源转换开关需要快速动作。目前,主要通过基于瞬时无功功率理论的dq0变换和αβ变换来检测电压故障,这些算法在检测到不对称故障时会产生误差。单相构造法计算准确,但是因为算法本身构造的问题会有60°的延时,对我国50 Hz的系统,即3.33 ms延时。为解决不对称故障时产生的误差以及算法构造带来的延时问题,提出了一种电压故障检测算法,其算法流程如图2所示。构造三相电压Ua求取单相电压导数,得出单相电压的余弦值,并通过三相电压之间的数学关系得出两相电压Ub和Uc,有效避免了单相电压构造法中只有a相电压采用实时数据,而b、c两相采用60°前的数据,导数构造法可使三相电压的采集数据具有同时性。通过dq0变换得到构造电压u d和u q,使用导数法对幅值进行提取,得到正序基波分量。传统的dq0变换和αβ变换,因电网的谐波分量导致电压检测到不对称故障时会产生误差。通过导数法提取电压正序基波分量,解决了低通滤波器的延时问题,并采用截止频率为3 k Hz的低通滤波器以避免对谐波分量产生干扰;计算正序基波分量和额定参考电压UN差值的绝对值再除以UN得出电压突变深度,由突变深度的绝对值D判断电源电压是否发生故障。

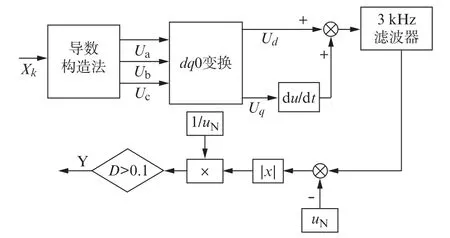
图2 电压检测算法流程

定义ω为角频率,t为时间,电源三相电压分别为

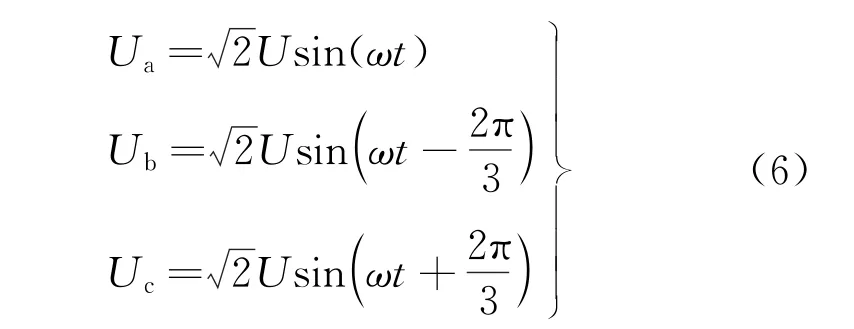
对a相电压求导得

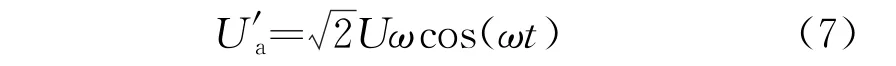
通过三相电压之间的导数关系可知:

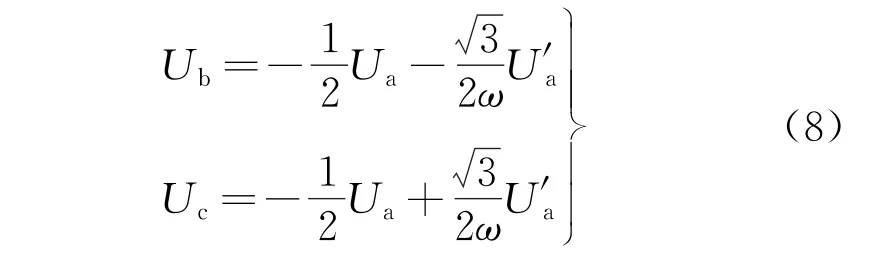
由导数关系构造出其余两相电压,可以解决单相电压构造法60°延时问题。

旋转矩阵为

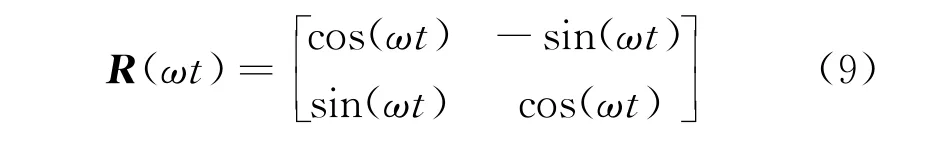
通过三相构造法得到三相电压,将abc坐标下的d轴正序分量和q轴正序分量,经dq0变换得到电压分量,其分量公式为

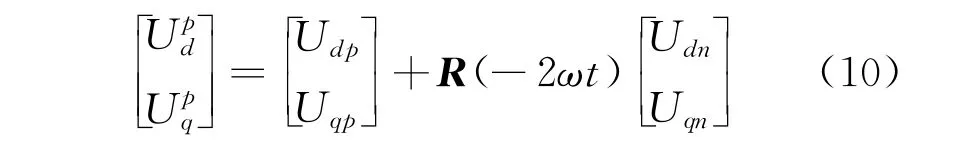
式中:U dp为变换后d轴电压U d的正序分量;U dn为变换后d轴电压U d的负序分量;U qp为变换后q轴电压U q的正序分量;U qn为变换后q轴电压U q的负序分量。

旋转90°后除以-2ωt得

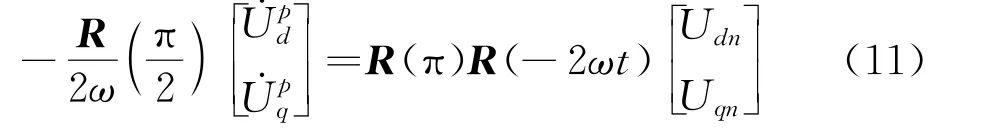
将式(10)、式(11)相加得

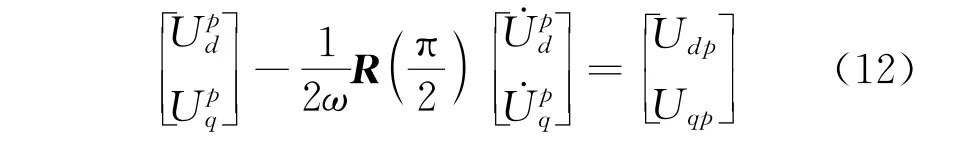
由式(12)可知,通过计算可得出正序分量,省去了dq0中的低通滤波器,保障了算法的即时正确性。依照图2电压故障检测算法流程可计算出电压突变深度绝对值为

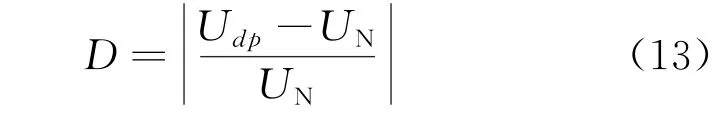
由IEEE定义的电压暂时变化可知,若电源电压变动的绝对值低于额定值的90%时,电能质量为不合格。通过式(13)中电压突变深度是否达到切换电源要求发出切换信号。

3 仿真验证

3.1 仿真模型的搭建

根据混合式双电源转换开关工作原理,在Simulink中搭建双电源自动转换开关仿真模型与电压故障检测算法模型,分别对电源电压可能发生的故障类型做仿真分析。双电源转换开关主回路拓扑结构如图3所示,其结构是在晶闸管开关上并联一个机械开关。工作原理为:当智能控制器检测到电压异常且达到电源切换要求时,控制器同时对常用电源1侧机械开关PS1和晶闸管开关TS1发出信号,使PS1断开,TS1导通;待PS1完成分断动作后,撤销TS1导通信号,负荷与电源1断开,等待TS1续流结束,控制器对备用电源2侧机械开关PS2和晶闸管开关TS2发出信号,使PS2闭合,TS2导通,负荷与电源2接通,待PS2完成闭合动作后,撤销PS1闭合信号和TS2导通信号,电源转换动作结束。

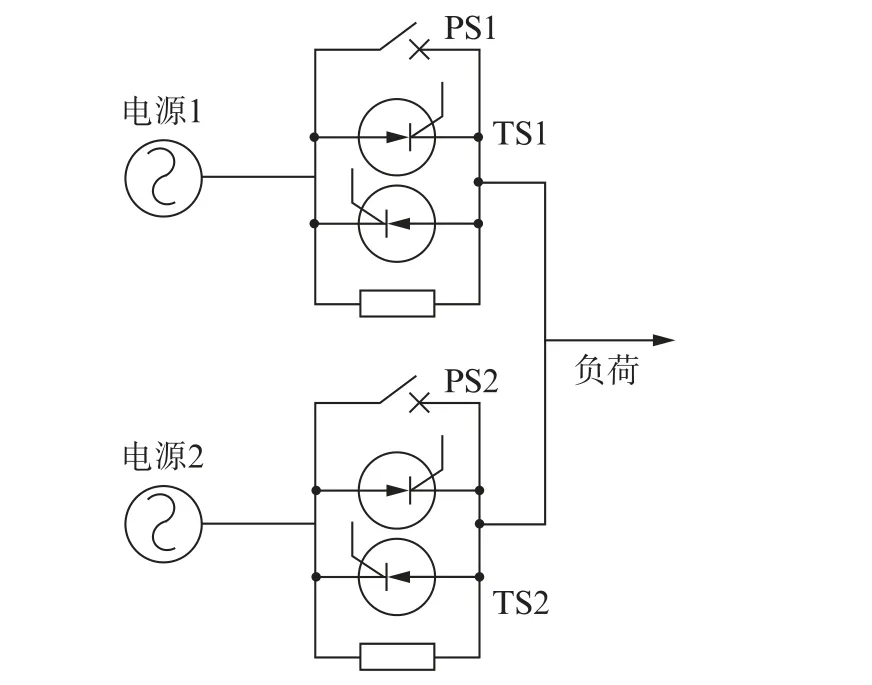
图3 双电源转换开关主回路拓扑结构

电压故障检测算法模型如图4所示。提取单相电压,考虑到存在白噪声环境,在真实系统和测量值上分别加入一个白噪声模块,设噪声幅值为115 V,噪声时间为3 ms,种子参数为默认值。将测量信号接入卡尔曼最优估计值模块,得到去噪后的电压采样信号。通过导数构造法构造其余两相电压,构造的三相电压经过dq0变换得到u d和u q。将三相正序电压基波分量与设定的参考值进行比较,若电压突变深度达到切换电源要求,控制器发出电源切换信号。

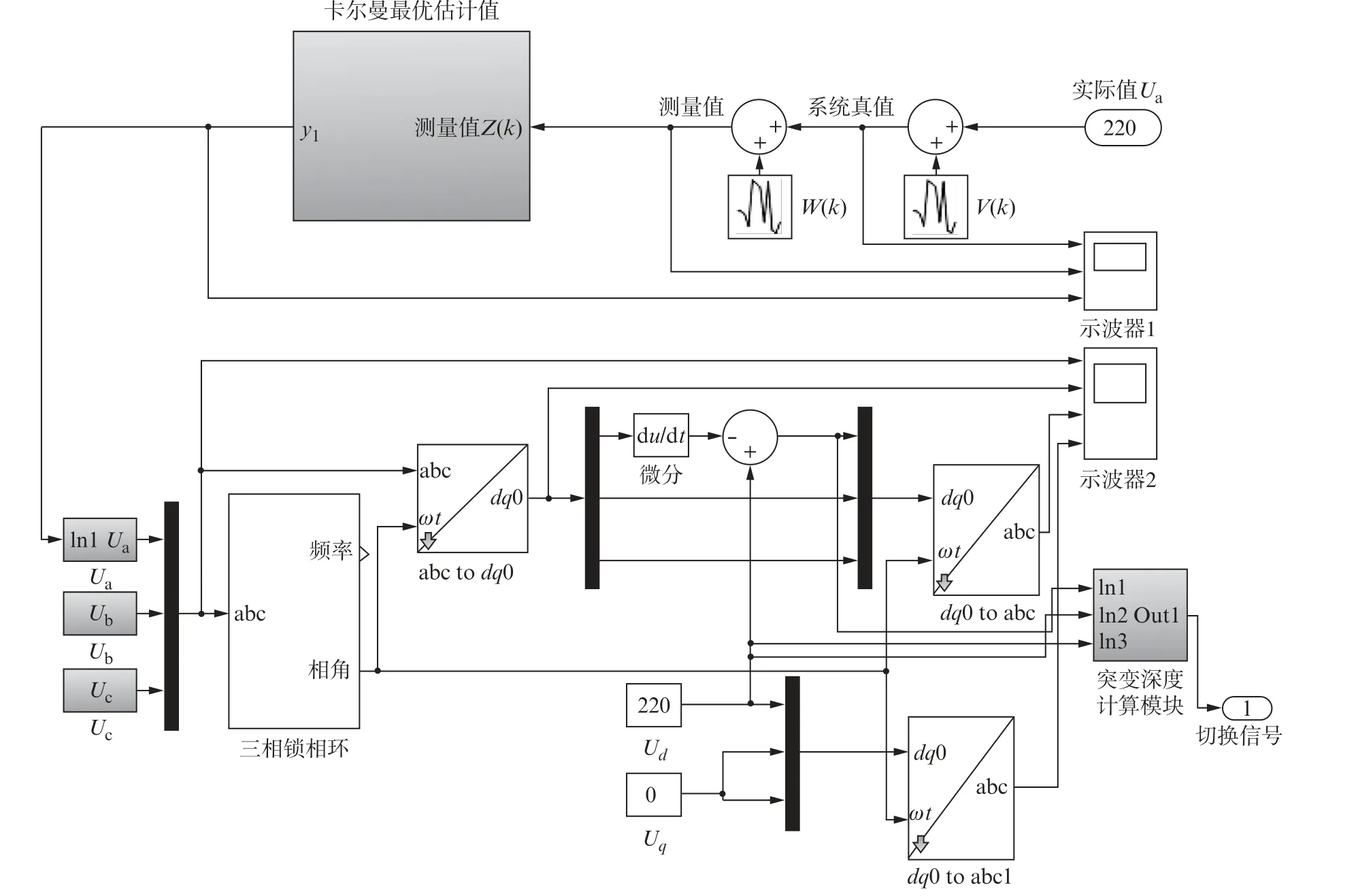
图4 电压故障检测算法模型

3.2 电压采样与滤波波形仿真

将采集的电源相电压信号经过整流、调理,变成模拟数字转换器可识别的0～5 V 的直流信号,通过Simulink对电源电压采样进行滤波,获得电压去噪前采样返回值;通过卡尔曼滤波对实测电压值进行去噪处理,得到电压去噪后采样返回值。电压采样去噪前后对比如图5所示。

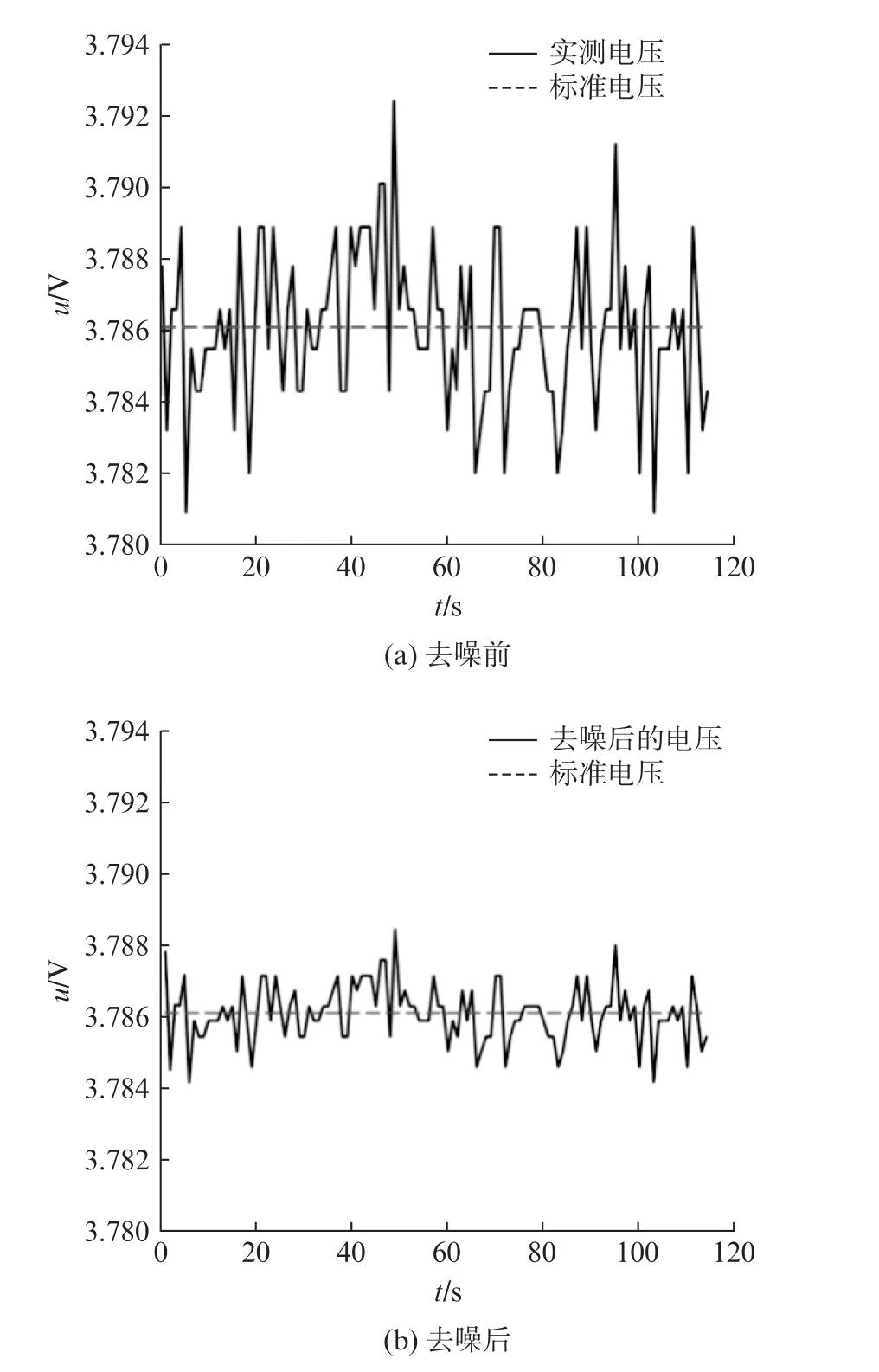
图5 电压采样去噪前后对比

由图5可见,采集的电压样本中干扰噪声和误差范围都较大,影响控制器对电压故障的判断,经去噪处理后效果明显,误差范围明显减小;电压误差范围由±0.17%缩小至±0.08%,降低了噪声产生的影响,使采样精度提升。

3.3 电压故障检测仿真

为了验证新型dq0算法的响应时间快速性,通过横向对比傅氏算法、dq0算法和小波变换法,在电压幅度突降20%、电压幅度突升20%以及单相电压突降20%的3种工况下进行仿真实验。图6所示为4种检测方法的仿真对比。表1给出了不同算法下混合式双电源转换开关控制器算法的检测时间。

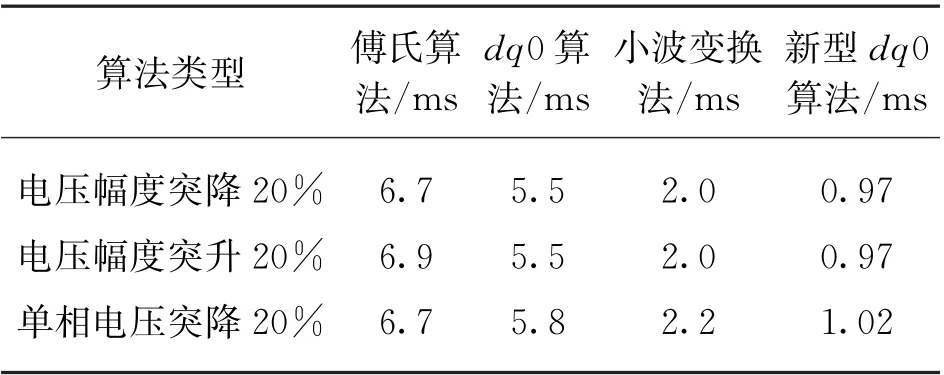
表1 不同算法在不同工况下的检测时间

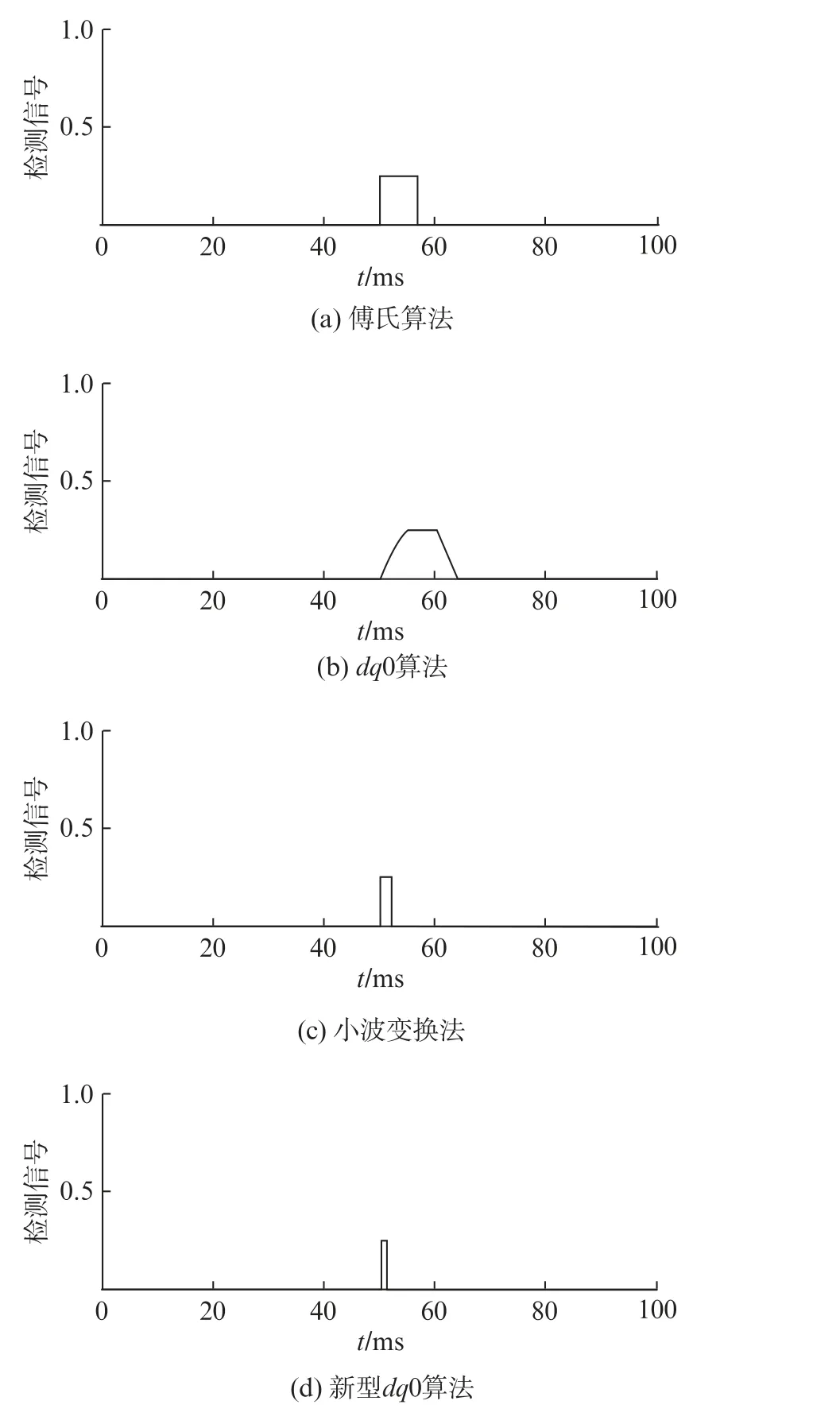
图6 不同算法的检测信号仿真图

由表1可知,从检测时间上,傅氏算法需要一个周期的电压采样数据,且受到低通滤波器的延时影响,其检测速度比其他3种算法慢;传统的dq0算法通过提取电压信号特征量,辨别电压突变信号对电压故障进行检测,但是由于其不可避免地受低通滤波器的影响,且我国工频系统存在固有的3.33 ms延时,使得该算法检测时间较长;小波变换法显著缩短了检测时间,但由于噪声对电压信号采集的干扰不能完全滤除,使小波变换无法精确提取一些电压特征量,可能导致故障误判;通过新型dq0算法可以同时采集三相电压的数据,并且采用导数滤波法省去了低通滤波器的使用,解决了其延时问题,将检测时间缩短至1 ms内。综合考量之下,本文研究的新型dq0算法检测时间相较另外3种算法更加优越,能够在较短的时间内检查到电压的突变。

4 结 语

本文研究了一种新型dq0算法,基于卡尔曼滤波理论对采样信号去噪,并利用数学关系对去噪后的单相电压构造三相电压,用导数滤波法省去了低通滤波器的使用。仿真实验表明:新型dq0算法解决了低通滤波器导致的检测延时问题,并且在电压突升、电压突降以及单相电压突降等工况下都有比较好的适应性,为电压故障检测算法的优化研究提供了参考。