自适应模拟退火混合粒子群算法的配电网故障定位

钱 程, 王爱元,2, 姚晓东,2

(1.上海电机学院 电气学院, 上海 201306;

2.佛山市高明区明革新型电机电控研究所, 广东 佛山 528500)

伴随着能源的大规模使用,新兴的分布式发电备受关注[1]。传统的配电网受到越来越多的分布式电源的并入带来的冲击,其结构越来越庞大,使得故障定位更加艰难[2]。然而,配电网发生故障后必须及时并且精确进行故障定位,然后进行电力隔离[3]。因此,配电网的故障定位问题一直是电力研究工作中的关注点之一[4]。

通过对馈线终端设备的合理运用,可以从配电网络节点及时得到准确的过电流、过电压等信息,从而利用这些信息完成对故障的定位操作[5]。使用遗传算法、粒子群算法、人工蚁群算法、蝙蝠算法、鲸鱼优化算法等各种优化智能算法去实现故障定位操作是目前比较流行的方法[6]。文献[7]采用遗传算法实现配电网故障定位,该方法可以简单地得到全局最优解,但是得到的结果却不够精确。文献[8-10]分别采用了蚁群算法、蝙蝠算法及蚁群退火算法实现配电网故障定位,这些方法鲁棒性较强,但由于其参数比较复杂,一旦设置出现偏差,会使得到的解偏离全局最优。文献[11]采用了改进的模拟退火算法实现配电网故障定位,该方法虽然提高了求解精度,但是过程太过复杂。文献[12]使用粒子群算法实现配电网故障定位,该算法在实现过程中耗时较短,得到的解可能是局部解,并不是全局最优解。以上文献采用的方法都是针对传统的配电网中产生的故障。

针对以上算法的缺陷,提出了一种基于自适应模拟退火混合粒子群算法。粒子群算法得到全局最优解的能力较弱,而模拟退火算法恰好可以弥补这一不足,再引入自适应寻优方案,使得改进的算法可以更适用于解决配电网故障定位的问题,更加快速并且准确地对故障进行定位,从而保证配电网的稳定运行。

1 配电网故障整数规划模型

1.1 传统配电网故障整数规划模型

如图1所示,在传统配电网中,G 表示配电网中的总电源,S1～S5表示开关节点,L1～L5表示各节点之间的馈线区间。因为在传统配电网中只存在一个电源,所以通常状态下过电流的方向是从G到普通节点。一旦产生故障,若节点处检测到过电流,则记作“1”;反之,记作“0”。因此,传统配电网一般的计算使用0-1整数规划模型[13]。各开关节点的状态值可表示为

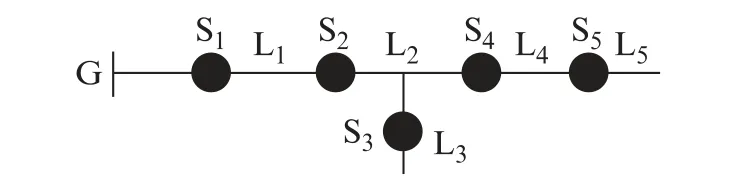
图1 传统配电网拓扑图

1.2 新型配电网故障整数规划模型

由于越来越多的分布式电源并入电网,电力生产波动增大,由此带来的冲击导致适用于传统配电网的0-1整数规划模型对新的配电网已不再适用[14]。针对这种情况,在原有模型的基础上,构建新的故障整数规划模型,如图2所示。

图2 新型配电网拓扑图

在原“0”和“1”的基础上,新增“-1”,共同表述新型配电网中各开关节点的状态值

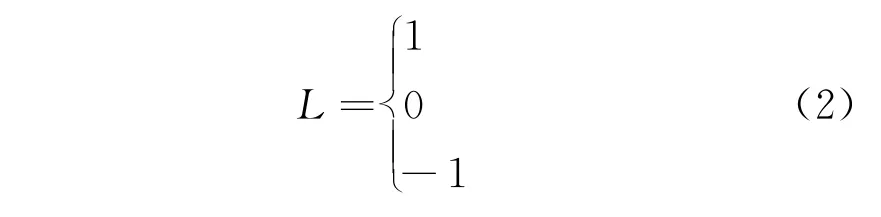
规定功率流由G 流向负载的方向为正方向,正方向的功率流且出现过电流记为“1”,反方向的功率流且出现过电流记为“-1”,没有出现过电流记为“0”。通过图2所示含分布式电源的新型配电网示意图来解释上述提出的新状态值公式。假设L3出现故障,此时节点S3处功率流为G 流向负载,存在正方向功率流并检测到过电流,记为“1”;节点S4处功率流为分布式电源DG1流向负载,存在反方向功率流并检测到过电流,记为“-1”。

1.3 开关函数的构建

通常情况下,开关函数是用来描述网络中节点状态的函数[15]。它可使算法更加合理地将馈线终端设备检测出的信息进行运用并加以分析后,得出故障区间[16]。

随着分布式电源不断接入配电网,传统开关函数已不能准确对其进行描述,传统开关函数的值为

式中:si为开关节点j下端第i个馈线区间的状态值。

对传统开关函数加以改进,构建改良的开关函数,使其可以更加精确地描述新型配电网,具体为

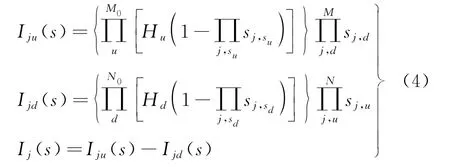
式中:I ju(s)、I jd(s)分别为开关节点j的上下端开关函数值;M0、M分别为上端的电源数量和馈线区间数量;N0、N分别为下端的电源数量和馈线区间数量;sj,su、H u分别为由上端电源到节点的状态和该区间电源的接入系数,若检测到电源,H u记作“1”,否则记作“0”,H d同理;sj,sd、H d分别为由下端电源到节点的状态和该区间电源的接入系数。

2 算法原理

2.1 模拟退火算法原理

模拟退火算法是在20世纪80年代被提出的,该算法的原理是模仿物体从升温到逐步降温的过程,目的是为了解决寻找全局最优的问题[17]。

模拟退火算法的实现分为两个过程:一个是算法过程,另一个则是退火过程。第一个过程的实现是根据20世纪50年代梅特罗波利斯(Metropolis)的采样方法,通过使用变化的量即概率去接纳最近出现的形式,被称为Metropolis准则。由此跳出局部最优解,是退火过程的前提。Metropolis准则中的相邻状态转化概率为

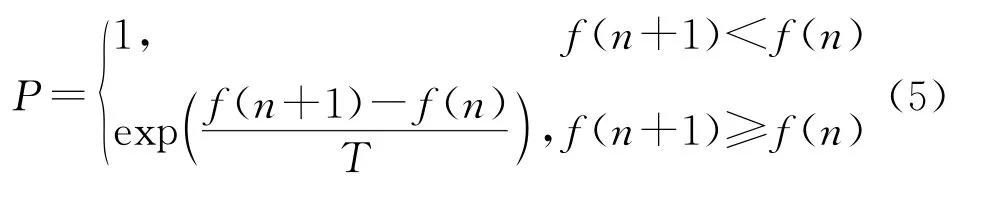
式中:f(n)为状态x(n)对应的能量;f(n+1)为下一状态x(n+1)对应的能量;T为控制参数,在初期T取较大值,随着过程的进行逐渐降低,进行若干次迭代,直到满足停止条件算法终止。

该算法利用温度的上升与降低达到控制算法搜索过程的目的,模拟退火算法流程如图3所示。

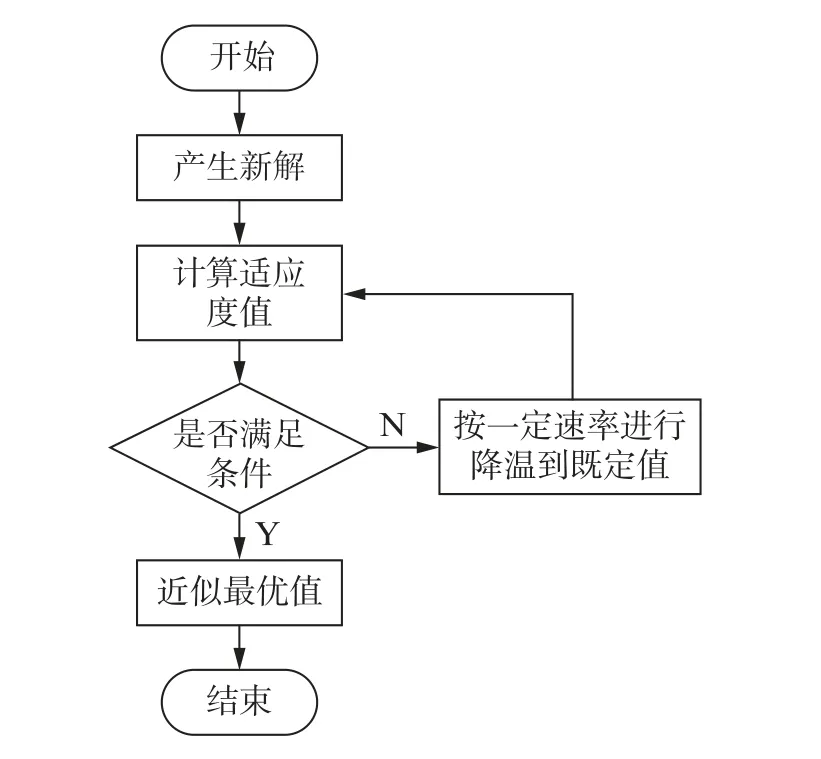
图3 模拟退火算法流程

2.2 混合粒子群算法原理

粒子群算法是在20世纪90年代中期由美国科学家提出的[18]。其原理是:首先,利用粒子的2个属性(速度和位置)更新,单个粒子在单独空间搜寻最优值,记作个体最优值;接着,跟整个群体共享对比,得到个体最优值,记作目前全局最优值;最后,将上述得到的2个值进行比较分析,以确定新的速度与位置,从而寻找全局最优。该算法的优势在于实现过程较为容易并且收敛时间较短,缺点是全局搜索能力不足。在原有公式基础上,更新得到混合粒子群算法的公式,具体为

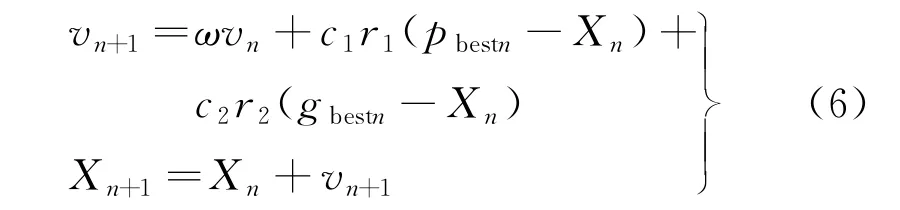
式中:X n为第n个粒子的状态;v n为第n个粒子的速度;pbestn为第n个粒子的最佳位置;gbestn为群体中所有粒子的最佳位置;ω为描述惯性的量;c1、c2分别为描述个体与整体速度的量;r1、r2为0～1之间的任意数值。

将ωv n看作变异的粒子,将c1r1(pbestn-X n)看作单个粒子与个体最优值交叉,将c2r2(gbestn-X n)看作单个粒子与当前全局最优值交叉。单个粒子位置与个体最优值交叉,单个粒子位置与当前全局最优值交叉,均保留优秀个体。变异操作跟交叉一样,也保留优秀个体。

2.3 自适应寻优方案

为了避免粒子群算法的弊端,以稳定算法为目的,提出自适应寻优方案,使其跳出局部最优的困境。在模拟退火算法与混合粒子群算法的混合算法中,假设连续冷却n次,并且每一次冷却都保持第n次冷却的全局最优值均比第n+1次冷却的全局最优值大,即gbestn-1-gbestn＜a(a是给定的某一正数),以判断算法是否陷入局部最优值[19]。若n≥M(M是给定的某一正整数),则使用自适应寻优的方案,得到新的个体;倘若不满足条件,则仍然使用原算法进行冷却。

当算法满足条件,采用自适应寻优并且得到新的个体D,在其最优解pbest邻域内依据正态分布产生随机扰动。自适应寻优策略如下:

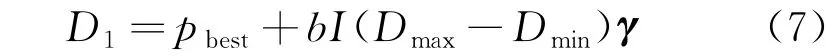
式中:D1为在D的基础上得到的新的个体;b为领域搜索半径;I为自适应因子,决定了该算法将通过一定概率去寻找最优解;Dmin、Dmax分别为D的上、下限;γ为单位向量;D=roundn(D1,O),O为Hadamard乘积。

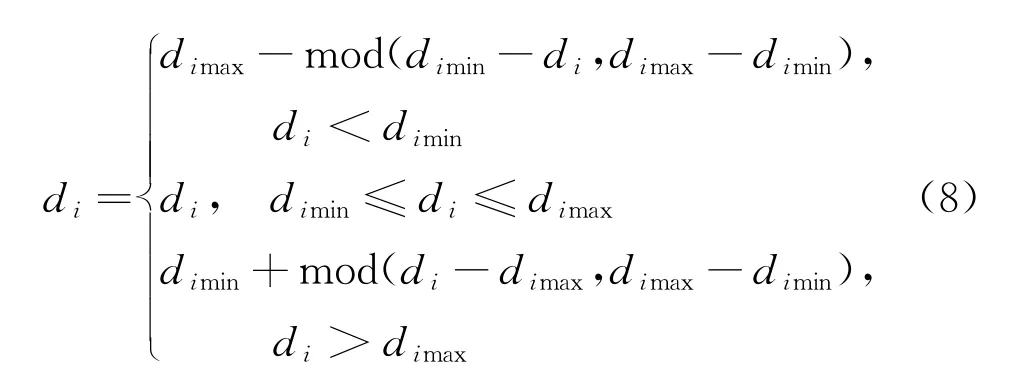
式中:mod(·)为取余运算;d i为D的一个元素,将D中重复的元素保留一个,再将缺失的元素补充进去,最终得到D。

邻域搜索半径为

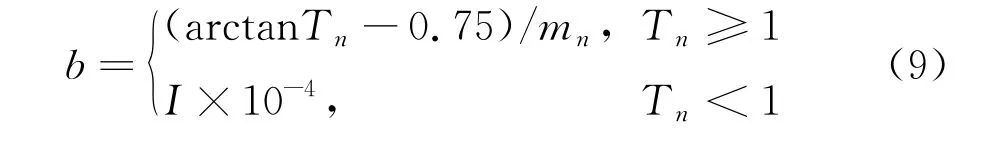
其中,

式中:T n为第n次冷却的温度;mn为(0,5)的随机分布;αi为(0,1)之间的随机数;β为自适应概率。

3 算法改进

3.1 自适应模拟退火混合粒子群算法故障定位

在配电网正常运行的过程中,一旦发生了故障,在配电网中的馈线终端设备会立即检测得到过电流信息。①通过含分布式电源的配电网故障整数规划模型,将检测得到的信息转变成故障向量;②通过开关函数将已经得到的故障向量转化成等效的向量;③将适应度函数作为目标函数,使用等效向量输入,从而得到粒子的最佳位置。将该位置作为算法的输出,然后通过仿真进行测试,从而完成对故障区间的判断。

3.2 适应度函数的构建

适应度函数也被叫作评价函数,在模型求解的过程中,它起着不可替代的作用,代表着由馈线终端设备上传的故障电流信息与开关函数的期望值之间的差值[20]。适应度函数值越小,表示结果越准确、合理,算法定位得到的区间越精确。传统的适应度函数为

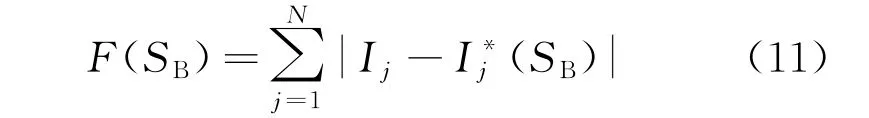
式中:SB为配电网当前状态下设备的状态值;N为配电网络中的节点总数;(SB)为描述开关函数均值的量。

分布式电源接入传统配电网,传统的适应度函数不再适用,在运算过程中可能会出现信息畸变甚至缺失,导致结果出现很大的误差。因此,提出了改进的适应度函数,以适用于含分布式电源的新型配电网。改进后的适应度函数为

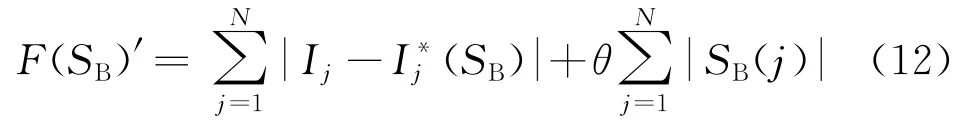
式中:θ为描述权重大小的量,在(0,1)之间取值。

3.3 算法流程

本文提出的改进算法流程如图4所示。图中,T n、T n+1分别为第n、n+1次冷却的温度;Tend为最终的温度;q为温度降低速率。

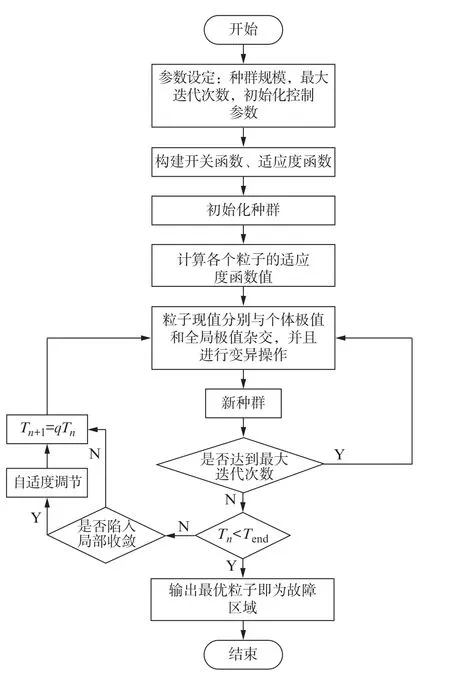
图4 改进算法流程

4 仿真分析

对IEEE 33节点有源配电网进行仿真,如图5所示。该网络有32条支路,电源网络首端基准电压12.66 k V,三相功率基准值取10 MVA,网络总负荷5 084.26+j2 547.32 k VA。在图5所示配电网中,G为传统电源,DG1～DG3为3个分布式电源,S1～S33为33个独立节点,L1～L33为33个馈线区段,K1～K3为DG1～DG3与电网相连的开关。

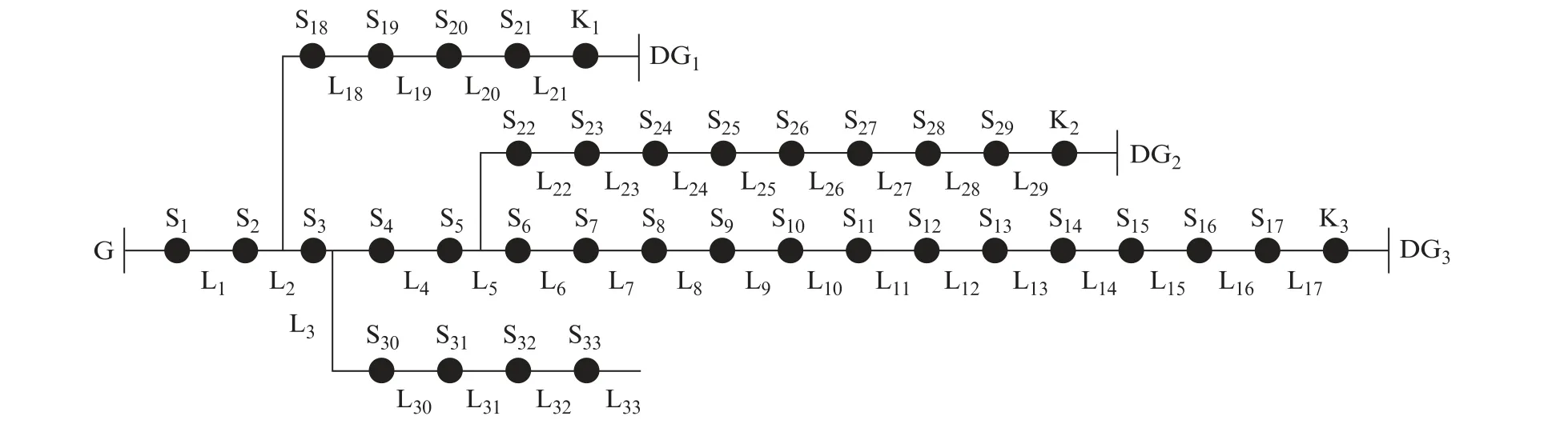
图5 IEEE 33节点有源配电网结构

4.1 算例分析

4.1.1 未接入分布式电源 当配电网中没有接入分布式电源,K1～K3均处于断开状态时,整个配电网系统为传统的配电网系统。

(1) 当配电网在某个单一区段发生故障时,在故障信息完整的情况下进行测试,参数选择θ=0.5,得到的结果如表1所示。

由表1可知,当配电网络中发生单一故障时,不管发生在哪一区段,算法都可以将故障区段精确定位出来。

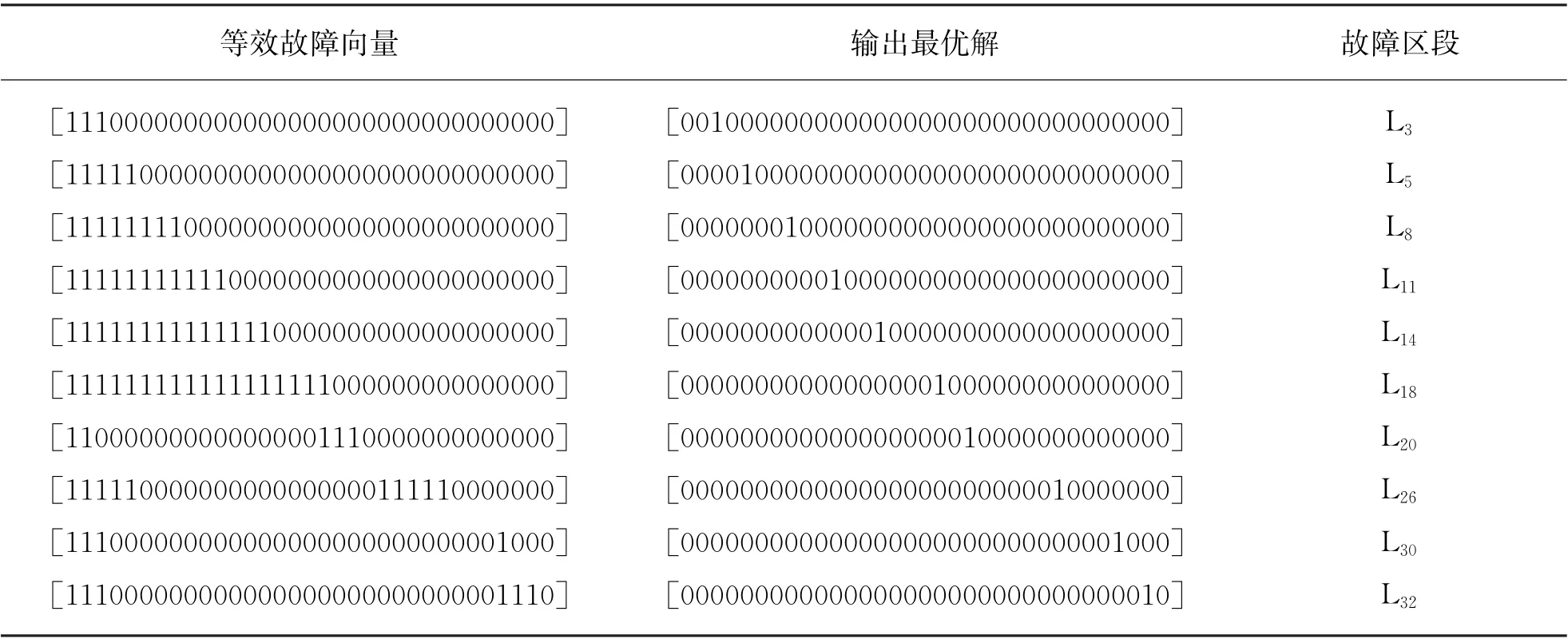
表1 配电网单一区段发生故障后定位仿真数据

(2) 当配电网在多个区段发生故障时,在故障信息不存在缺失的状态下进行仿真测试,测试所得的数据如表2所示。

由表2可知,当配电网络中同时发生多个故障时,不管发生在哪几个区段,算法依然可以将故障区段精确定位出来。

表2 配电网多个区段发生故障后定位仿真数据

4.1.2 接入分布式电源 分布式电源接入到配电网中,此时整个配电网模型与传统配电网模型不同,为含分布式电源的有源配电网模型,K1～K3处于部分或全部合上的状态。在此模型下,对配电网中不同故障定位进行分析,如表3所示。

由表3可知,当配电网络中发生故障且存在信息丢失或畸变时,提出的算法依然可将故障区段精确定位出来。

表3 新型配电网发生故障后定位仿真数据

4.2 对比分析

为了验证本文所提混合算法的优势,把该混合算法与模拟退火算法、混合粒子群算法进行对比分析。

4.2.1 快速性对比分析 在单一故障信息无缺失、单一故障信息有缺失、多故障信息无缺失、多故障信息有缺失4种故障状态下进行仿真测试,3种算法的迭代曲线如图6所示。

图6中,图6(a)的状态是L14为故障区段且故障信息无缺失;图6(b)的状态是L14为故障区段且故障信息无缺失,同时S5、S7、S13故障信息缺失;图6(c)的状态是L15、L26为故障区段且故障信息无缺失;图6(d)的状态是L15、L26为故障区段且故障信息无缺失,同时S4、S8、S12故障信息缺失。由图6可见,随着故障区间的增加或故障信息的缺失,模拟退火算法与混合粒子群算法所用的迭代次数明显增加,自适应模拟退火混合粒子群算法所用的迭代次数变化不大且在3种算法里最少。由此可见,本文提出的自适应模拟退火混合粒子群算法在故障定位时更加快速并且有一定的容错性。

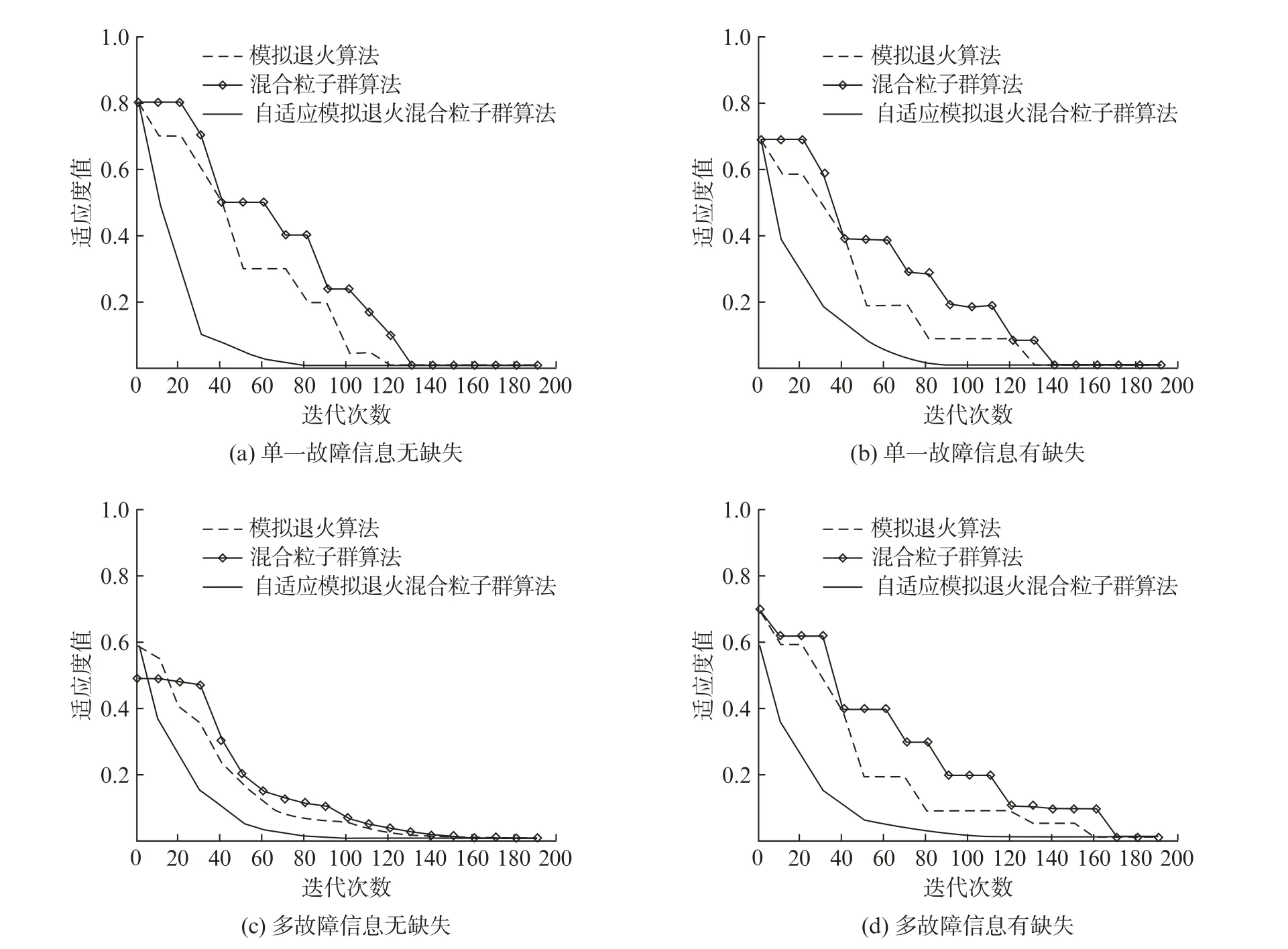
图6 不同故障类型的算法迭代曲线对比图

4.2.2 准确性对比分析 以上述4种故障状态为例,分别进行40次仿真测试,得到的仿真结果如表4所示。

由表4可知,当配电网中出现多故障并且伴随信息畸变或缺失的时候,模拟退火算法和混合粒子群算法的准确性较低并且容错性较差,反观本文提出的自适应模拟退火混合粒子群算法,在面对上述情况时,故障定位更加准确且容错率更高。

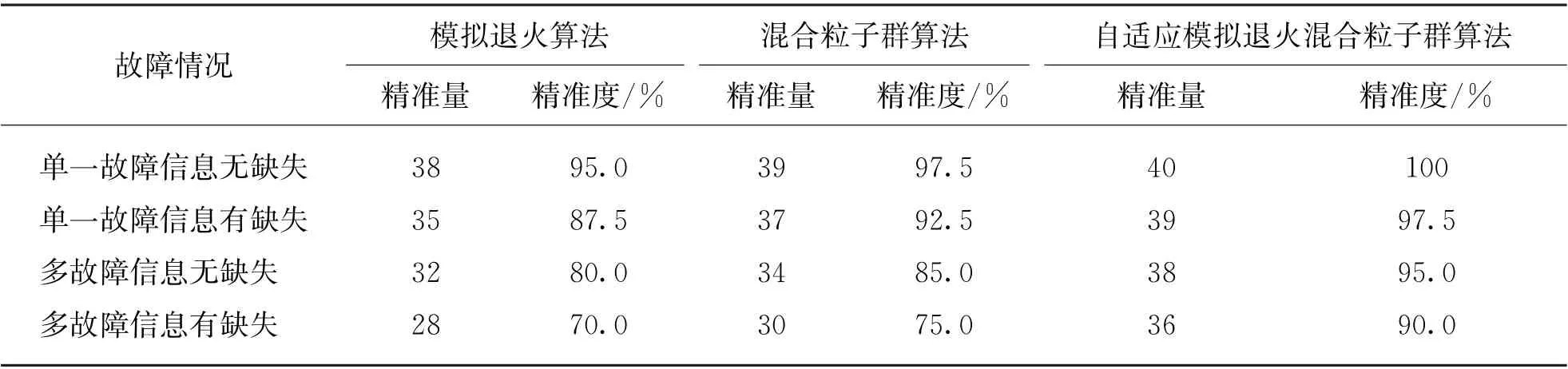
表4 算法准确性对比

5 结 语

本文提出了自适应模拟退火混合粒子群算法,对有源配电网发生故障后进行定位分析,并与模拟退火算法及混合粒子群算法进行对比分析,验证了自适应模拟退火混合粒子群算法在配电网故障定位的过程中结果更精确,收敛更快速,针对不同的情况具有一定鲁棒性。