基于复杂样本的安全态势要素分类架构

2022-08-29何春蓉

重庆邮电大学学报(自然科学版) 2022年4期

何春蓉，朱江，张欣

(重庆邮电大学通信与信息工程学院，重庆 400065)

0 引言

近年来，随着云计算、5G通信、人工智能等技术的快速发展，互联网技术突飞猛进，人们对网络的需求大幅度增加。然而，由于网络收集和存储了大量用户的隐私数据，网络安全治理问题引起了各行各业的广泛关注。网络安全态势感知[1]主要是获取、理解、评估导致网络环境中网络态势变化的网络安全要素信息，并预测其发展趋势，从而实现主动、动态的安全防御。态势要素获取是进行大规模网络安全态势感知的重要前提和基础，通过对网络中各种网络设备产生的具有海量、异构、多维等特征的数据进行统计分析和识别，并最终形成态势要素。

态势要素分类处理的数据是异构、多维的，直接处理会导致实时性差、分类精度较低。特征降维方法能够很好地降低高维数据、提取重要特征、消除冗余特征。因此，解决态势要素获取的关键是找到一种数据降维的方法，在低维空间进行分类，提高分类精度[2]。如文献[3]提出一种基于卷积神经网络(convolutional neural network，CNN)的网络入侵检测模型，采用不同的降维方法去除网络流量数据中的冗余和不相关特征，利用CNN自动提取降维数据的特征，通过监督学习提取更有效的入侵识别信息；文献[4]提出一种基于反向传播的深度自编码网络(deep auto-encoder network-back propagation，DAN-BP)的入侵检测模型，训练DAN获得低维特征数据集，然后利用BP算法对学习到的低维数据进行分类识别；文献[5]提出一种结合集成K-means聚类和自编码器(ensemble K-means and auto-encoder，EKM-AE)的入侵检测方法，该方法利用训练好的自编码器进行入侵检测；文献[6]提出结合深度堆栈编码器和反向传播算法的安全态势要素提取方法，利用编码器提取数据集特征进行降维。以上方法虽然在一定程度上解决了网络数据冗余的问题，却没有考虑到现实中收集到的网络攻击数据中各类攻击记录存在数量不平衡的问题，从而导致小样本训练不充分，分类精度远远低于大类样本的问题。

深度神经网络通过组合低层特征形成抽象的高层表示，可以自动提取高级潜在特征并进行分类，无需人工干预[7-9]。为了更好地处理异构、多维的网络安全数据，提升复杂样本的分类精度，本文提出一种基于条件变分自编码(conditional variational auto-encoder，CVAE)[10]网络的安全态势要素分类架构。CVAE是一种重要的生成模型，主要包括编码网络和生成网络，且结构是对称的。在编码网络中嵌入一个独热编码的标签向量进行监督学习；将指定标签的低维隐变量输入生成网络中，生成指定的新攻击样本，提高复杂样本的分类精度。同时混合密度模型的使用优化了条件变分自编码网络的特征提取能力，提高了生成网络重构数据的相似性[11]。本文的主要研究内容如下。

1)训练基于混合密度模型的深度条件变分自编码网络(mixture density networks-deep conditional variational auto-encoder，MDN-DCVAE)，使用训练样本训练MDN-DCVAE，并记录训练数据集中每类攻击样本的最大重构损失值。

2)利用MDN-DCVAE生成网络生成指定类别的新攻击样本，根据1)中保存下来的类别最大重构损失筛选新攻击样本，将符合条件的新生成的攻击样本合并到原始训练数据集中。

3)进行分类、合并后的训练数据集用于训练分类器，训练后的分类器用于识别测试数据集中的攻击。

1 基于MDN-DCVAE的安全态势要素分类架构

为了解决网络环境中采集到的大规模复杂安全数据的分类问题，本文提出一种面向复杂样本，基于深度条件变分自编码网络的安全态势要素分类架构，并从网络架构、模型训练、样本扩充和样本分类进行详细介绍。

1.1 网络架构

本文所提具体网络架构如图1所示，该架构中CVAE网络的关键问题是如何采样隐变量z去重构原始样本，而隐变量z是一个未知且复杂的分布，因此，无法随意选择它的分布。一个可行的方案是在生成网络之前加一个编码网络，将训练样本及其标签c一起输入编码网络进行训练来获得隐变量z的分布[12]，根据不同的样本标签将训练样本强制分配到不同的分布中，即隐变量z在低维特征空间中按类别分布。生成网络拥有同编码网络对称的网络结构，将隐变量z尽可能地重构为原始样本。比较重构样本和原始样本的区别，通过损失函数衡量网络训练的程度，得到最佳的网络权值等参数。

图1 安全态势要素分类架构

1)样本的扩充。该部分主要由生成网络和混合密度模型组成，通过输入指定样本标签生成攻击样本，从而平衡训练数据，提高少数攻击的分类精度。混合密度模型对样本扩充的贡献主要体现在模型的损失函数上。

2)样本的分类。采用MDN-DCVAE中的编码网络作为分类器，由编码网络去掉最后一层后加上一层softmax网络组成，其训练过程分2步进行：①采用编码网络的权值初始化基分类器的隐藏层权值；②生成网络生成新的攻击记录与原始训练集合并后对分类器进行监督学习，微调分类器权值，训练好后的分类器用于复杂样本的分类。

1.2 模型训练

分类架构中，主要包括2个操作：样本的扩充和样本的分类。采用训练好的生成网络用于样本扩充，编码网络用于样本的分类，因此，需要对模型进行预训练，得到最优的网络参数并保存下来，直接加载训练好的模型进行样本的扩充和分类。下面对该模型的主要训练过程及原理进行详细介绍。

1.2.1 DCVAE模型

深度条件变分自编码网络主要包含2部分：编码网络和生成网络。使用深度神经网络主要是利用其自动提取高级特征的特性，可以更好地解决复杂、大规模、非线性的网络攻击样本的分类问题。模型训练的具体过程如下。

步骤1本文的训练数据为多维的攻击数据和对应的标签，假设输入的安全样本集为x=[x1,x2,…,xi]，对应的标签集为c=[c1,c2,…,ci]，则神经网络输入i个样本，每个样本有n个维度，具体表示为

(1)

(2)

(1)—(2)式中：xi为单个的多维网络攻击数据点；ci为该网络攻击数据点对应的标签；n、k为数据预处理后的维度。由于攻击数据具有多个属性，属性中存在离散变量和连续变量，预处理中对所有的离散变量进行独热编码，对所有的连续变量进行归一化操作。

步骤2将训练数据输入编码网络，求得编码网络的概率分布参数(均值和方差)并从中采样出低维隐变量z的采样值。将采样后的隐变量z及其相应的标签输入进生成网络进行数据的重构。

步骤3根据模型的损失函数不断优化网络参数，为了简单处理，将网络的损失函数分解为多个数据点损失的总和。单个数据点xi的损失函数lDCVAE(xi,ci,φ,θ)表示为

logp(xi|ci)≥lDCVAE(xi,ci,φ,θ)=

-DKL(qφ(z|xi,ci)‖pθ(z|ci))+

Eqφ(z|xi,ci)(logpθ(xi|z,ci))=

-DKL(qφ(z|xi,ci)‖pθ(z|ci))+

(3)

1.2.2 基于混合密度模型的DCVAE模型

DCVAE模型训练的损失函数越小，说明模型训练得越好，其中，损失函数的重构损失项衡量了重构样本的准确性。MDN可以通过对每个混合成分求取权重系数并进行线性组合来建模目标数据的条件概率分布，得到每个输出值的概率，以获得数据的完整表示[12-14]。本文提出生成网络联合MDN来生成重构样本，利用混合密度模型优化条件变分自编码器的特征提取能力，提高重构数据的准确性，得到更准确的重构样本，其贡献主要体现在模型训练的损失函数中，具体的实施方法如下。

在给定输入隐变量z时，通过生成网络和混合密度模型得到重构数据的概率密度函数，其具体定义为

(4)

(4)式中：m为高斯分布中混合成分的个数；αj为第j个成分的权重系数；μj和δj分别为混合高斯分布第j个成分的均值和方差。

为了确保混合密度模型的输出参数能够形成有效的分布，需要将输出参数通过适当的函数进行处理以确保其值在有意义的范围内。(5)式使用softmax函数约束混合权重为正且和为1，(6)式约束标准差为正。具体的处理方式为

(5)

(6)

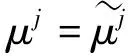
(7)

(5)—(7)式中，αj、δj、μj分别为混合密度模型输出的第j个分布的混合权重、方差和均值。因此，基于混合密度模型的DCVAE的损失函数重新定义为

logp(xi|ci)≥lMDN-DCVAE(xi,ci,φ,θ)=

-DKL(qφ(z|xi,ci)‖pθ(z|ci))+

Eqφ(z|xi,ci)(logpθ(xi|z,ci))=

-DKL(qφ(z|xi,ci)‖pθ(z|ci))+

(8)

在网络的训练过程中，使用Adam算法训练MDN-DCVAE，最小化模型损失函数以得到最优的网络参数φ和θ。由于梯度下降算法的反向传播过程无法处理从中采样得到的隐变量z，因此，对其采用重采样操作将z重新参数化为确定性函数，具体方法为

z=μ+δζ，ζ～N(0,1)

(9)

(9)式中：μ为编码器输出的均值；δ为方差。

1.3 样本的扩充

采用训练好的生成网络用于样本扩充，然而生成网络生成的新攻击样本可能存在较大差异，新生成的样本可能会偏离原来的攻击样本分布。为了更好地选择新生成的攻击样本，该架构根据类别计算每个训练样本的重构损失，然后以每个类的最大重构损失作为筛选标准，挑选适合的样本数据，其具体操作如下。

生成网络pθ(xi|z,ci)联合MDN，其概率密度函数为

(10)

数据的对数似然函数为

l(xi,ci)=logpθ(xi|z,ci)=

(11)

(4)式中，L为隐变量z的采样个数，通常为1。

生成网络输出MDN的混合权重、方差和均值，然后求得该类别生成样本的损失值。将损失值与训练模型时保存的每类攻击样本的最大重构损失值进行对比。假设某类别的最大重构损失为

maxL=max(l(xi,ci))

(12)

以该类别的最大重构损失值maxL作为选取新攻击样本的筛选标准。若新生成的样本的重构损失大于该类的最大损失，则丢弃此样本，反之，将其融入新训练样本集中对编码网络进行微调。

1.4 样本的分类

采用训练好的DCVAE网络中的编码网络作为基础，去掉最后一层神经网络用softmax网络代替。作为一种有监督的分类器，softmax网络可以很好地学习类别同数据之间的特征关系，对编码网络提取到的低维态势特征向量进行分类并微调整个分类器。softmax将多个神经元的输出映射为(0,1)的实数，并保证它们的和为1，通过softmax函数就可以将多分类的输出值转换为(0,1)且和为1的概率分布。假设编码网络输出的低维矢量为X，其类别为c，则属于该类别的概率计算式为

yc=p(Y=c|X,W,b)=

(13)

式(13)中，W和b为最后逻辑回归层的权重和偏置值；I为输出节点的个数，即分类的类别个数。

2 态势要素获取算法流程

本文针对网络安全数据的特点，采用深度神经网络作为分类器对获取的网络安全样本进行分类识别。针对其高维性，采用条件变分自编码网络中的编码网络进行降维处理，同时生成网络联合混合密度模型用于扩充样本数量较少的攻击数据，提高生成数据的准确性，其贡献主要体现在模型训练的损失函数中。算法流程如图2所示，主要包含3个步骤。

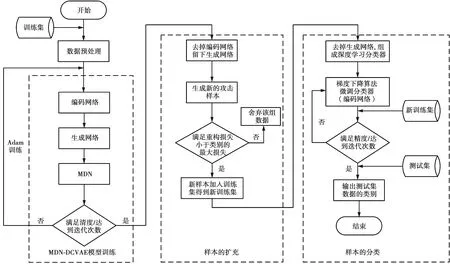
图2 态势要素获取算法流程

步骤1MDN-DCVAE模型训练。该模型主要由编码网络、生成网络、混合密度模型3部分组成。

步骤2样本的扩充。利用生成网络生成新的攻击样本，将符合的样本与原始训练集合并形成新的训练集。

步骤3样本的分类。训练好的编码网络去掉最后一层，然后加上一层softmax网络组成分类器，通过反向传播微调分类器，得到最优的分类模型，将测试数据集输入分类器得到分类结果。

3 仿真分析

3.1 网络安全数据的选取

本文实验使用的是NSL-KDD数据集，它是KDD-CUP99数据集的改进版本。训练集主要由21种攻击类型组成，并且测试集中额外有16种训练集不包含的攻击类型，攻击主要分为4大类：DOS攻击、U2R攻击、R2L攻击和Probe攻击，其余为正常数据，每类样本都有相应的标签。NSL-KDD训练集和测试集中每个类别的具体个数如表1所示。

表1 NSL-KDD数据集类别分布

3.2 实验数据预处理

NSL-KDD数据集有41个特征，其中有9维连续变量，32维离散变量。对所有的离散变量进行独热编码，对所有的连续变量进行归一化操作，然后将每条记录扩展为121维特征向量。采用下面的方法对连续变量进行归一化处理

(14)

(14)式中：x′为归一化后的数据；xmin、xmax为输入数据每个特征的最小值和最大值。

本文的实验环境为：Windows 10操作系统，python3.7环境下采用Keras深度学习框架进行模型训练和测试。硬件配置为：64位操作系统，处理器为Inter(R)Core(TM)i5-8500 CPU 4.00 GHz。

3.3 最优模型结构的确定

基于深度神经网络的条件变分自编码器，其降维效果依赖于深度神经网络(deep neural network，DNN)的结构。随着层数的增加，编码网络对于原始数据的特征提取能力逐渐增强，但层数过多也可能会降低模型的泛化能力。同时通过文献[15]可知，隐含层的节点数对于分类结果同样非常重要。由于DNN具有自动提取特征的能力，因此，隐藏层的节点数量以2的倍数递减的方式进行设置，其值为{100，80，60，40，10}。为了得到最优的网络结构，设置不同深度和不同隐藏层节点数的条件变分自编码器进行对比实验，选取性能最优的结构设置作为最终的模型结构。由于本文模型使用的误差函数是根据模型的优化情况进行改进的，因此，本文采用计算得到的误差函数来评价模型训练的好坏，实验结果如表2所示。

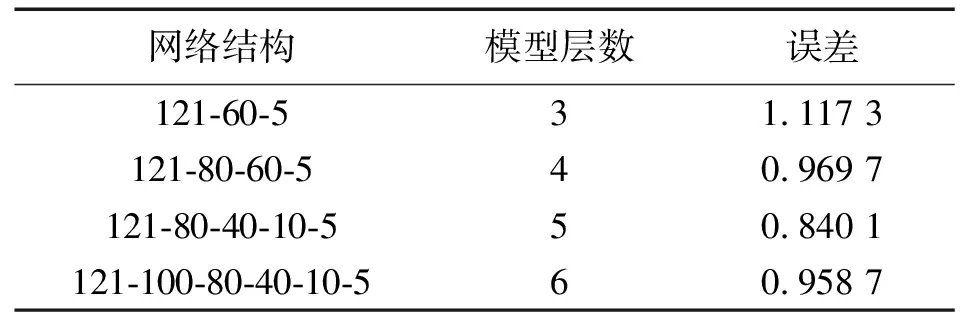
表2 不同结构的模型分类精度

从实验结果得知，该模型在NSL-KDD数据集上的最优网络结构为121-80-40-10-5，其中，训练数据通过预处理后的维度为121维，需要分类的攻击类型为5类。网络结构中，输入层有121个神经元，低维输出层有5个神经元。5层网络结构的DNN具有更小的训练误差，层数过深或过浅都会导致误差增加，因此，选取5层的深度神经网络结构作为条件变分自编码器的基本网络结构进行数据降维和分类。

分别训练具有以上4种网络结构的MDN-DCVAE，并将训练好的编码网络作为分类器比较不同网络结构对攻击的分类效果，结果如图3所示。从图3可以看出，模型在未进行数据平衡之前，每种网络结构计算出来的攻击的分类精度都不同。具有5层深度神经网络结构的模型具有更好的分类精度。隐含层较多会降低模型的泛化能力，提高模型的抽象能力，数据处理时反而会曲解原始信息，从而降低分类精度；隐含层过少，模型的抽象能力较差，无法高度概括数据的隐含特征，也会降低模型的分类精度。

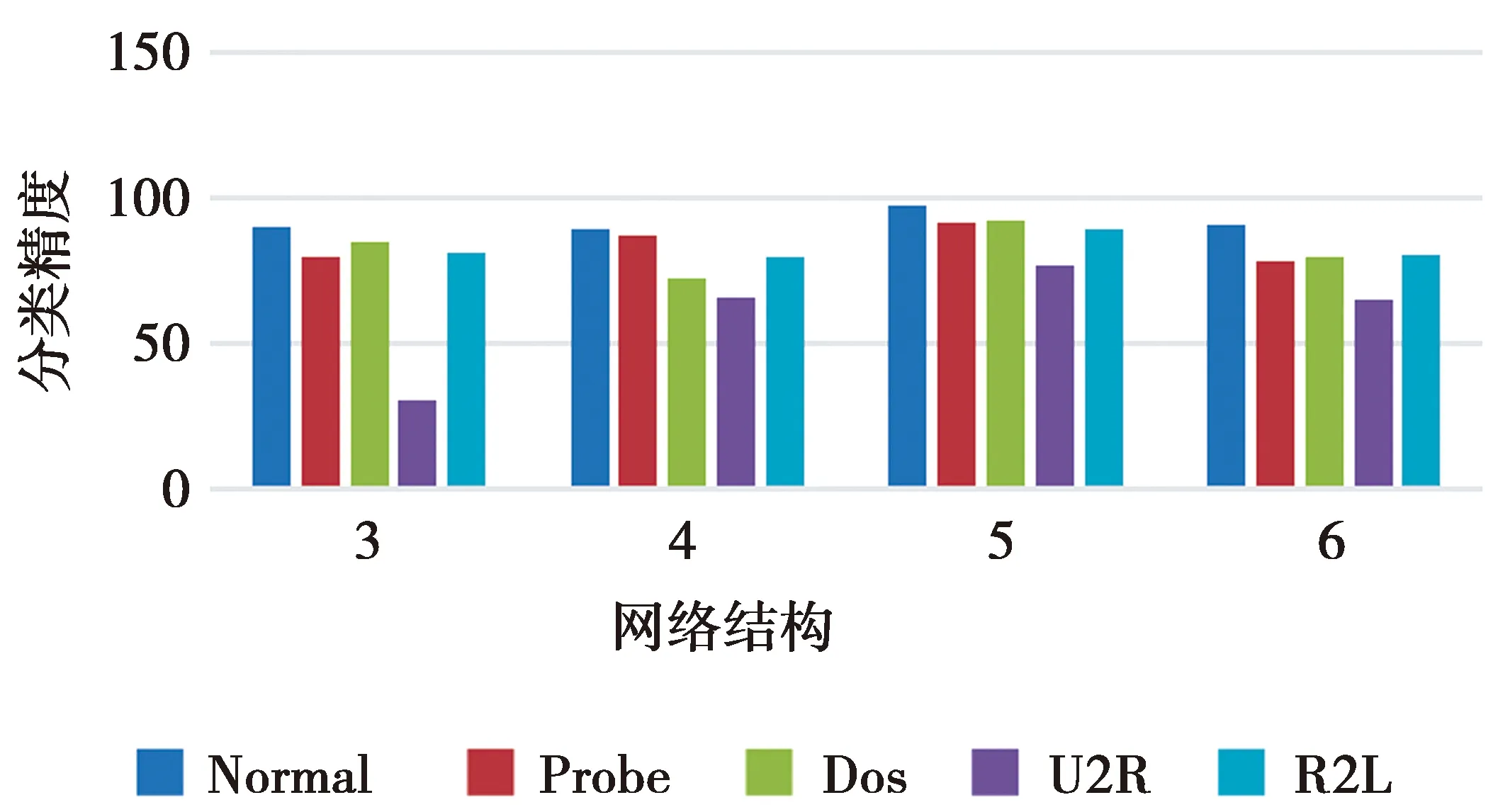
图3 各模型分类精度比较

3.4 降维效果分析

本文提出条件变分自编码器用于高维数据的降维，同时迫使多类别的数据在低维空间根据类别聚类。为了更清楚地突出MDN-DCVAE的降维优势，将其同主成分分析(principal component analysis，PCA)法、传统自编码(auto-encoder，AE)网络的降维效果进行比较，得到的可视化效果图如图4所示。实验中使用以上方法将输入的高维数据降维并投影至2维空间。在图4中，相同颜色的圆点为同一类别的数据。如果相同颜色的圆点靠得越近，能够轻易地与其他颜色的圆点分开，则降维效果越好。

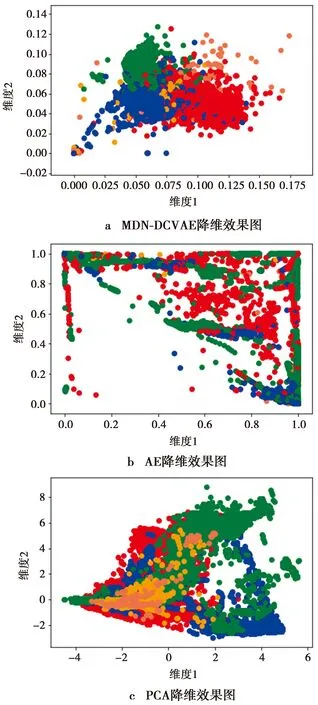
图4 各模型降维效果对比图

对比图4的图片可以看出，本文所提出的MDN-DCVAE相比其他模型具有更好的降维效果。由于MDN-DCVAE的方法为非线性降维，深度神经网络可以将高维数据转换为低维数据，随着网络层数的增加，能够提取更多数据的抽象特征，因此，提供了比主成分分析更强大的非线性泛化能力。而PCA是线性降维方法，将其用于非线性数据的特征提取将会损失大部分的特征信息，如果需要使用PCA用于非线性数据特征的提取，应该对其进行改进或与其他模型进行结合，弥补其处理数据的缺陷。传统的AE网络相比深度自编码网络具有较少的隐藏层，因此，对数据抽象特征的提取能力远不及MDN-DCVAE，降维效果不理想。

3.5 MDN-DCVAE对小类样本数据的影响

从表1可以看出，NSL-KDD数据集是不平衡的，其中U2R和R2L只有少量记录。分别用MDN-DCVAE和DCVAE的生成网络生成指定类别的多条记录来平衡训练数据，使得每种类别的数据数量相同，结果如表3所示。

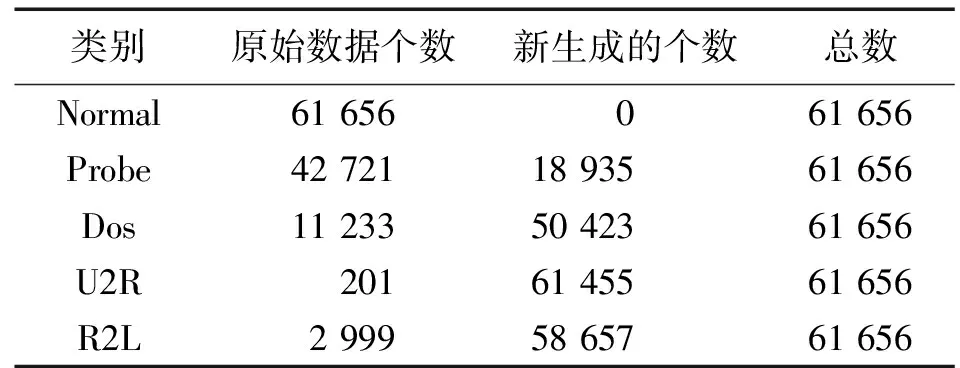
表3 NSL-KDD数据集平衡后的样本数

平衡数据后微调模型再做分类处理，将数据输入微调后的分类器进行分类精度的比较，结果如图5所示。

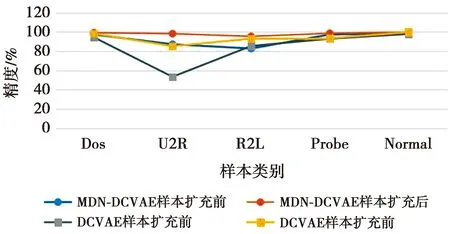
图5 平衡数据前后精度对比图

从图5可以看出，在样本扩充前，由于U2R和R2L记录较少，模型并未很好地提取到该类别的特征，导致分类精度较低，但MDN-DCVAE相对于DCVAE具有较高的分类精度，说明本文所提模型中混合密度模型的使用可以提高重构数据的相似性，得到更准确的重构样本。样本扩充后，每个类别数据的数量相同，模型可以公平地捕捉每个类别的特征，因此，较少数量样本的分类精度有所提高。

3.6 分类器收敛性分析

本文采用MDN-DCVAE的编码网络作为分类器，其网络结构为3.3节确定下来的5层神经网络结构。图6为分类器的误差变化情况，图7为分类精度变化情况。从图6、图7可以看出，随着迭代次数的增加，误差逐渐降低，分类精度逐渐增大，网络达到收敛。说明本文提出的模型框架具有较好训练效果和泛化能力。

图6 误差随迭代次数的变化曲线

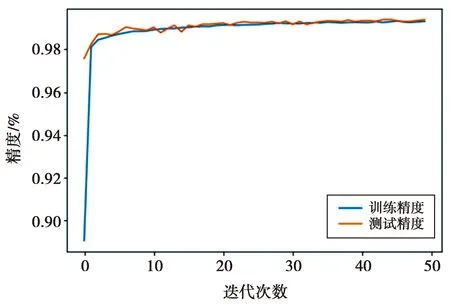
图7 精度随迭代次数的变化曲线

3.7 分类精度分析与比较

为了评估本文所提模型的攻击分类能力，将本文方法同传统AE、未做任何改进的CVAE、基于支持向量机的核主成分分析法(kernelized principal component analysis-support vector machine，KPCA-AVM)[16]和DAN-BP[4]进行比较，其中，AE和CVAE均采用本文网络结构的确定方法，采用3层感知机结构，以交叉熵作为损失函数，激活函数为relu，迭代次数、学习率和本文方法相同；DAN-BP[4]使用DAN获得新的低维特征数据集，利用BP算法对学习到的低维数据进行分类识别；DAN采用5层网络结构；BP采用4层网络结构；KPCA-AVM[16]中，SVM的核函数采用高斯函数，正则化参数设置为1.35。将测试集输入进训练好的模型后得出分类结果，如表4所示。

表4 不同方案的态势要素获取精度

4 结束语

针对网络安全数据具有多维、异构和冗余等问题，本文提出一种面向复杂样本的态势要素分类架构，以深度神经网络作为基本网络框架，与传统的多层感知器相比，具有更快的学习速度，可以从训练数据集中自动提取高级抽象数据。同时深度条件变分自编码网络的生成网络能够根据指定的攻击类别生成攻击样本，平衡训练数据集。该分类架构将特征提取、样本扩充和分类集成到一个无需大量启发式规则和人工经验即可自动提取特征并分类的系统中，提高了系统的效率。采用NSL-KDD数据集对本文所提模型进行仿真实验，证实了该态势要素分类架构的有效性和准确性。