职前教师自我效能感与计算思维水平关系研究——基于天津某师范大学的个案研究

陈孝钟

(南开大学滨海学院，天津300270)

1 引言

计算思维作为21世纪人才必备的能力[1]，自2006年周以真教授首次明确提出以来，广受国内外研究者的关注。计算思维有助于提高学习者提升日常工作问题解决中的分析技能和问题抽象能力[2]，使得现代社会中许多工作受益于计算思维[3]。教育工作者有必要让每个人都可以接受计算思维教育[4]。教育工作者能够教授计算思维的前提是自身能够很好理解计算思维并且能够知道如何教授计算思维，世界上已有很多国家将计算思维教育纳入课程教学体系中[5]。自我效能感指个体对自身行动控制的直觉或者信念[6]，是Bandura社会认知理论中核心的概念[7]。自我效能感水平对个体的思维、行动[8]以及问题解决[9]等方面有着重要的影响。当前有关教师效能感的研究主要围绕入职和在职教师进行[10]，已有研究表明：教师的教学实践以及学生学习成果与其自我效能感之间存在着紧密的相关性[11]。对职前教师的计算思维水平与自我效能感之间的关系进行探究有着重要的现实意义，同时也为职前教师计算思维的研究提供了一个新的视角。

2 研究问题

文章使用问卷调查法，通过使用SPSS进行统计分析，欲解决如下问题：

1)探究职前教师自我效能感与计算思维水平之间是否存在关联？

2)若二者存在关联，则进一步探究二者之间存在什么样的关系？

3)职前教师自我效能感对其计算思维水平的哪些方面有较大的影响？

3 研究设计

3.1 研究对象

文章的调查对象为天津某师范大学具有教师资格证且计划从事教师行业的本科生。本次调查共发放问卷300份，回收有效问卷286份，文章基于此数据集展开相关分析。

3.2 研究工具

1)自我效能感量表

一般自我效能感量表(General Self Efficacy Scale,GSES)由Schwarzer及其合作者共同编制的，在国际上被广泛应用于一般自我效能的测量。中文版的GSES 最早由张新建等人修订，该量表信效度良好[12]。量表共包含10 个题项，各题项从“完全不正确”到“完全正确”，采用1～4 计分。本次调查中该量表的Cronhach’s Alpha为0.877。

2)计算思维量表

Korkmaz 及其合作者编制的计算思维量表CTS(Compua‐tional TinkingSales)被学界广大研究者广泛应用于计算思维水平的测量[13]。该量表包括“创造力”“算法思维”“协同”“批判性思维”“解决问题”五个维度，共计29个题项，各题项从“非常不赞同”到“非常赞同”，采用1～5 计分。本次调查中该量表的Cronhach’s Alpha为0.799。

4 结果分析

使用SPSS 26.0对所收集的数据集进行数据正态分布分析，本次调查样本量较大，故选择K-S检验，结果如表1所示。结果表明各项数据P值均小于0.05，表明各项数据均不符合正态分布。

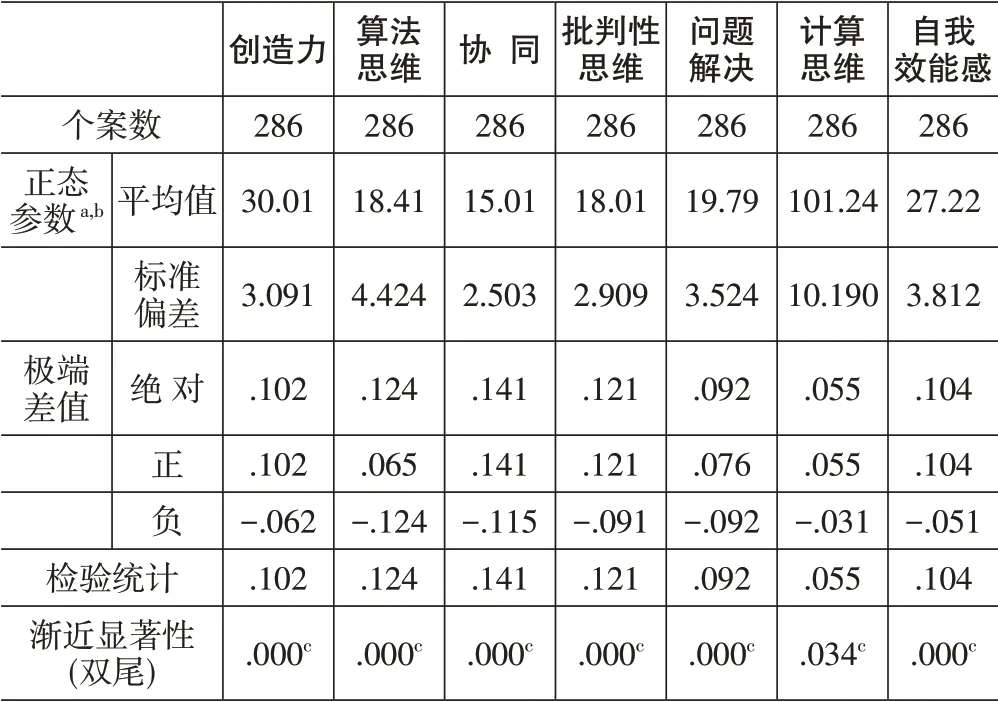
表1 数据集K-S正态检验结果

4.1 职前教师计算思维水平与自我效能感相关性分析

为进一步分析职前教师计算思维水平与自我效能感是否相关？采用Spearman相关性分析对数据集进行分析，结果如表2所示。结果显示P值<0.01，且相关系数为0.619>0，说明职前教师的计算思维水平与其自我效能感之间存在着显著的正向相关，至此第一个问题得到解决。

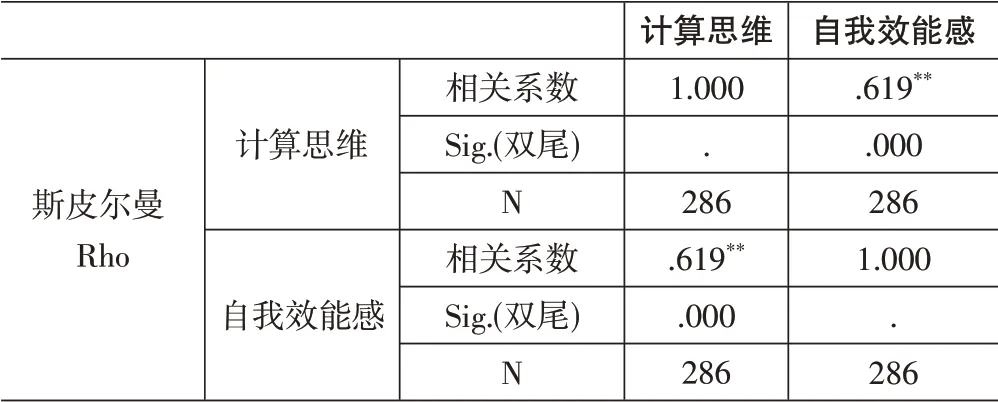
表2 职前教师计算思维与自我效能感相关性分析结果

4.2 职前教师自我效能感与计算思维水平关系分析

为进一步探究职前教师自我效能感与计算思维水平之间的关系，以自我效能感为自变量X，计算思维水平为因变量Y，使用SPSS 26.0进行回归分析。通过观察散点图，发现二者并非呈现明显的线性关系，采用曲线估计，结果显示S型曲线模型的拟合优度最优，调整后的R方为0.45，具体参数如表3所示。

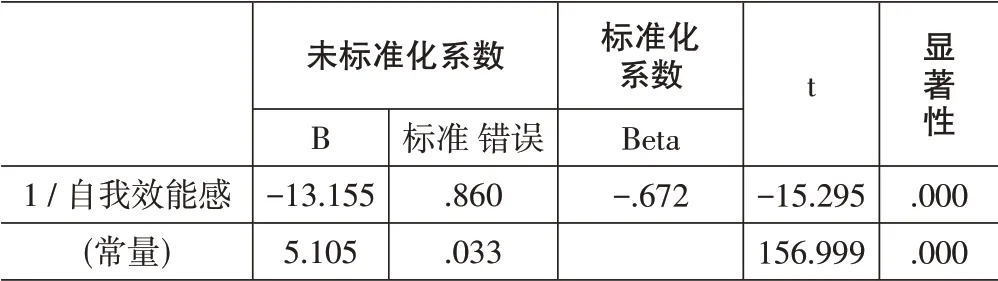
表3 S型曲线模型回归分析系数表

由表3结果可知P值<0.01，该模型具有显著性。由此得出二者的回归方程如下所示，至此第二个问题得以解决。

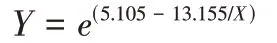
根据回归方程可以得出以下结论，整体来看对于职前教师的自我效能感越高，其计算思维水平越高，较之自我效能感较高者，自我效能感较低人员通过自我效能感的提升，可获得更快的计算思维水平提升。

文章采用的CTS 量表包含5个维度，为进一步了解自我效能感对计算思维中各维度的影响关系，进一步对各维度与其自我效能感之间的关系进行探究。由前面K-S检测结果可知，各项数据不符合正态分布，采用Spearman 相关性分析，结果如表4 所示。结果显示，自我效能感与计算思维中的协同维度在0.05水平上呈正向相关关系，与其余各维度均在0.01水平上呈现显著的正向相关关系。

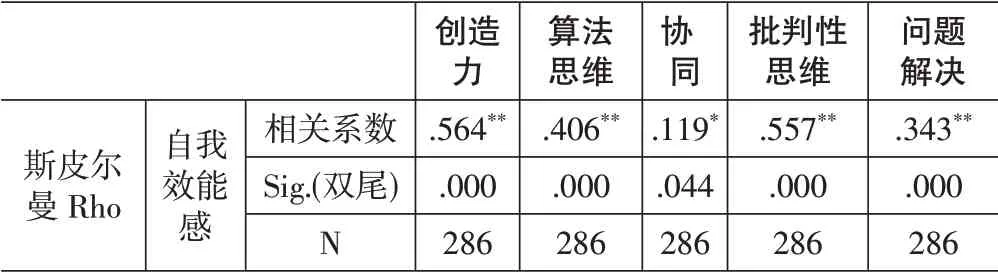
表4 计算思维各维度与自我效能感相关性分析结果

以自我效能感为自变量X，以计算思维中的创造力为因变量Y1进行回归分析，通过散点图发现二者线性关系不明显，进一步使用SPSS 的曲线估计功能，分析结果显示在幂曲线模型的拟合优度最高，调整后的R方为0.354，具体参数如表5所示。

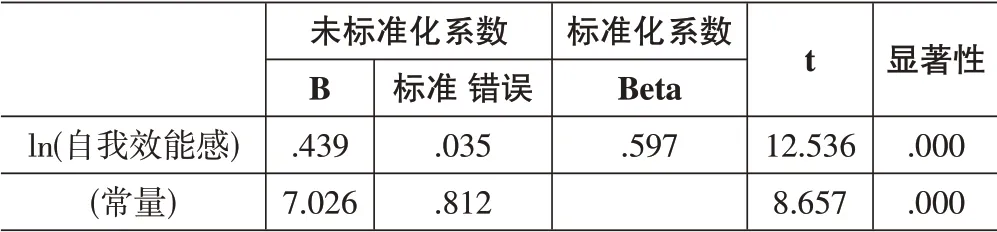
表5 自我效能感与创造力回归分析结果

由表5结果可知P值<0.01，说明该模型具有显著性。由此得出二者的回归方程如下所示：

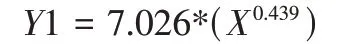
同以上步骤对算法思维Y2，协同Y3，批判性思维Y4，问题解决Y5分别进行回归分析得到Y2最优拟合模型为逆模型，调整后的R方为0.185，Y3最优拟合模型为二次模型，调整后的R方为0.021，Y4 呈线性关系，调整后的R 方为0.401，Y5 最优拟合模型为三次模型，调整后的R 方为0.151,由于Y2、Y3、Y5 的调整后的R 方均较低，说明该模型解释力不足，在此不予以考虑。对于Y4，具体参数如表6所示：

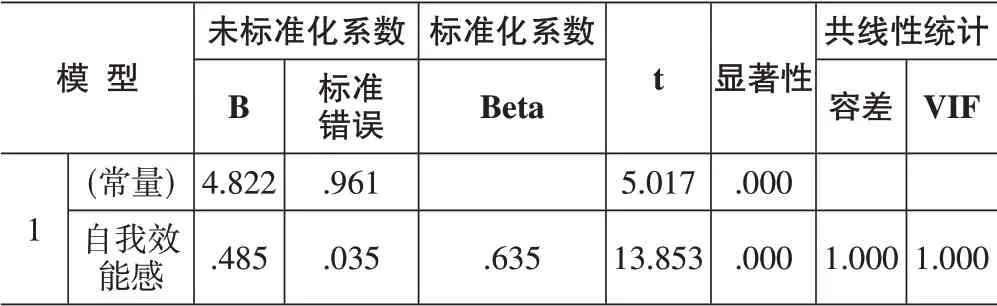
表6 自我效能感与批判性思维回归分析结果

由表6 可知，P值小于0.01，说明该模型具有较强的显著性，由此得到如下回归方程：

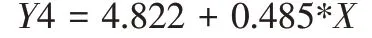
5 结论及启示

5.1 结论

通过上述的分析可以得出如下结论：

1)职前教师的自我效能与其计算思维水平之间存在正向相关关系，且二者的关系为S型曲线关系。

2)职前教师的自我效能与其计算思维中的创造力存在正向相关关系，二者的关系为幂关系。

3)职前教师的自我效能与其计算思维中的批判性思维各维度存在正向线性相关关系。

4)职前教师的自我效能与其计算思维中的算法思维、协同以及问题解决维度存在显著的相关关系。

5.2 启示

综合前文研究结论，可以对职前教师的计算思维的培养提供以下几点参考：

1)对于自我效能感较低的职前教师，可以通过提升其自我效能感，达到快速提升其计算思维水平的目的。

2)注重职前教师正确职业意识的培养。

有研究表明正确的职业意识可以提升职前教师的自我效能感[14]，故而可以通过提升职前教师的正确职业意识，来促进其计算思维水平的提升大有裨益。只有教师理解并掌握了计算思维，方能较好地将其应用到实际工作中，促进计算思维教育的发展。

3)注重榜样以及成功经验的作用。

榜样的作用及成功的经验有利于帮助 职前教师不断地发现自我、认识自我，对自我效能感的提升有着巨大的促进作用[15]。

4)注重职前教师的反思意识的培养。

有效的反思是促进个人学习和发展的重要力量，也是提升教师自我效能感的有效途径[16]，更是计算思维的重要组成要素。

5)采用方式多样化的教学方式。

网络学习空间能有效提升学习者自我效能感[17]，利用网络学习空间开展相应的课堂教学，提升职前教师的自我效能感，进而达到提升其计算思维水平的目的。